1°/ Le paradoxe de Condorcet : Phénomène non transitif.
2°/ Conjecture de FERMAT Puissance niéme :
3°/ Duplicité du cube :
4°/ Trisection d’un angle :
5°/ Le problème de Syracuse :
6°/ La Conjecture de Goldbach :
7°/ Le Problème de Catalan :
8°/ Elkies contredit Euler :
9°/ Le paradoxe de Zénon d’Elée : La flèche
10°/ L’avocat :
11°/ Le segment qui se voulait aussi grand qu’une droite… :
12°/ \sqrt{2} = 2 :
13°/ Factorielles et carrés :
14°/ Fractions égyptiennes :
15°/ Équations Diophantiennes :
16°/ Côtés et segments remarquables du triangle :
17°/ Les distances d’un point aux sommets d’un carré :
18°/ La brique parfaite d’Euler :
19°/ Le paradoxe d’Épiménide le Crétois :
20°/ Quelques sophismes :
21°/ Le barbier barbant :
22°/ Le paradoxe de Zénon d’Elée : Achille et la tortue
23°/ Paradoxe de Socrate et Platon :
24°/ Les nombres de Ramsey :
25°/ Les nombres de Lychrel :
26°/ Le nombre chromatique du plan :
27°/ Persistance multiplicative :
28°/ Paradoxe des anniversaires et Rubik’s cube :
29°/ Le plus court chemin est-il la ligne droite ?
30°/ \pi = 4 ou même 2 :
31°/ Les bœufs d’Helios :
32°/ Pythagore nous aurait menti ?
33°/ L’Algorithme de Kaprekar :
34°/ Le paradoxe du duc de Toscane, ou la naissance des probabilités :
35°/ La conjecture de Poincaré :
36°/ La loi de Benford :
37°/ Des sommes de réel étonnantes :
38°/ Les 7 problèmes du millénaire :
39°/ Le paradoxe de Bertrand :
40°/ La trompette de Gabriel :
41°/ Le paradoxe de Simpson : étude sur les placébos
42°/ Tous les triangles sont équilatéraux :
43°/ Les limites de bon sens :
44°/ Je suis le Pape :
45°/ Le paradoxe de la roue d’Aristote :
1°/ Le paradoxe de Condorcet : Phénomène non transitif.
Un phénomène transitif respecte l’ordre. Donc : si A < B et B < C alors A < C.
Cependant il existe des phénomènes non transitifs. Ainsi : si A < B et B < C alors A > C.
Chaque résultat l’emporte sur un autre. C’est comme dans le jeu du Chifumi (Pierre-papier-ciseaux), chaque action l’emporte sur une autre.
1°/ L’élection :
Soient trois candidats ou trois options, A, B et C que nous voulons départager par le vote. Si une majorité d’électeurs préfère A à B, nous noterons A>B.
On peut imaginer que si A>B et B>C alors A>C. Et bien cela est faux en général comme le prouve l’exemple suivant.
Lors de l’élection du délégué de classe de 3°2, trois candidats se sont présentés : Véronique, Jules et Olivier.
Dans cette classe de 25 élèves, j’ai donc demandé à chacun de donner ses préférences.
5 élèves préfèrent Jules à Véronique, elle-même préférée à Olivier : J > V > O : 5 voix
Voici les résultats :
J > V > O : 5 voix
J > O > V : 6 voix
O > J > V : 3 voix
O > V > J : 3 voix
V > O > J : 7 voix
V > J > O : 1 voix
Total : 5 + 6 + 3 + 3 + 7 + 1 = 25 élèves
Donc on remarque que :
5 + 6 + 3 = 14 préfère J> V contre 3 + 7 + 1 = 11 pour V > J
5 + 7 + 1 = 13 préfère V>O contre 6 + 3 + 3 = 12 pour O > V
3 + 3 + 7 = 13 préfère O>J contre 5 + 6 + 1 = 12 pour J > O
On a donc J > V, V > O et pourtant O > J alors qu’on s’attendrait à J > O !
Autrement dit aucun classement tel que J > V > O ne peut être considéré comme le classement préféré de la classe, car celui-ci impliquerait que J > O. Dans ce cas, les classements individuels ne peuvent conduire à un classement collectif.
Voici 3 types d’élections :
1/ L’élection précédente s’appelle Vote plurinominal, à un tour, avec échelle de préférences. C’est le vote le plus démocratique par excellence. Avec trois candidats, l’électeur a le choix entre 6 combinaisons possibles. Malheureusement, ce mode de scrutin, qui permet à l’électeur d’exprimer un ordre de préférence sur l’ensemble des candidats, est difficilement applicable dans la pratique. Il butte sur le paradoxe de Condorcet et il y a impossibilité de désigner un vainqueur.
2/ Vote uninominal, à la majorité simple, à un tour. C’est le système anglo-saxon : First past the post. Celui qui remporte le plus de voix au premier tour est élu. Ici se serait Jules car il a 14 voix contre 13 pour Olivier et Véronique.
3/ Vote uninominal, à la majorité absolue, à deux tours. C’est le système français. Il faut avoir plus de la moitié des voix pour être élu au premier tour, sinon on réalise un deuxième tour. Dans ce cas de figure, si Olivier se désiste au profit de Véronique (ou le contraire), Jules est battu au deuxième tour par 26 voix contre 14 (si le report est total).
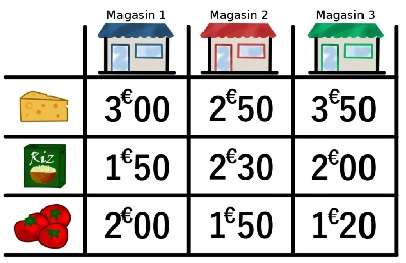
2°/ Les magasins :
Les enseignes de distribution de vantent souvent d’être moins chère que leurs concurrents. Mais est-ce 3 magasins peuvent être plus économiques à la fois les uns avec les autres ?
| Voici 3 magasins qui vendent 3 produits identiques. | Comparons les magasins 1 et 2. C’est 2 qui est plus économique. |
 |
 |
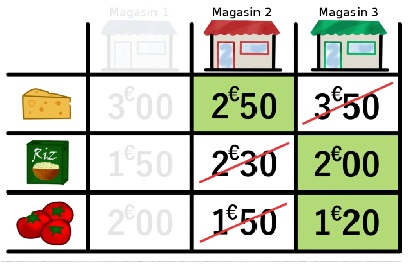
| Comparons les magasins 2 et 3. C’est 3 qui est plus économique. | Comparons les magasins 1 et 3. C’est 1 qui est plus économique. |
 |
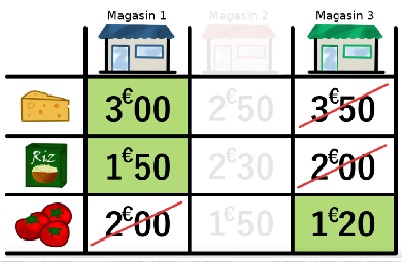 |
Donc : Magasin 3 < Magasin 2 puis Magasin 2 < Magasin 1 mais Magasin 1 < Magasin 3 ???? Il n’y a pas de magasins plus économiques que les autres, cela va dépendre du produit.
Les publicitaires ont encore de beaux jours devant eux pour nous vendre leurs salades.
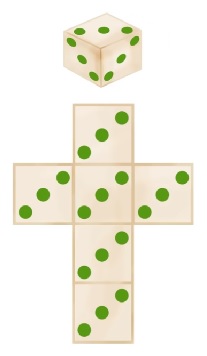
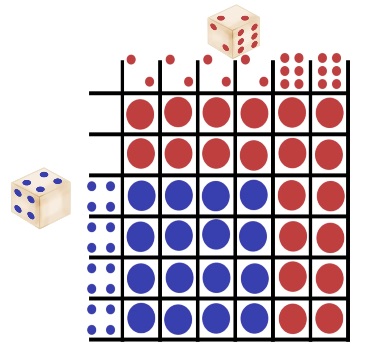
3°/ Les dés :
Voici 3 dés un peu particulier. Lequel a le plus de chance de nous faire gagner ?
 |
 |
 |
Représentons les issues possibles et leurs résultats sont forme de tableau :
 |
 |
 |
 |
 |
 |
Le dé vert est meilleur que le dé rouge qui est lui-même meilleur que le dé bleu, il semble logique de supposer que le dé vert sera meilleur que le dé bleu. Est bien contrairement à ce que l’on pouvez imaginer, le bleu l’emporte sur le vert !!
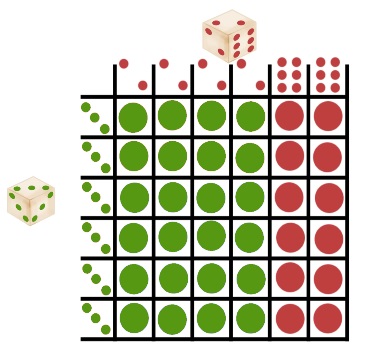
Mais on peut encore aller plus loin : voici 3 nouveaux dés et leurs résultats.
Le 1ier dé vert est meilleur que le 2ième dé rouge qui est lui-même meilleur que le 3ième dé bleu, mais c’est bien le bleu qui est meilleur que le vert.
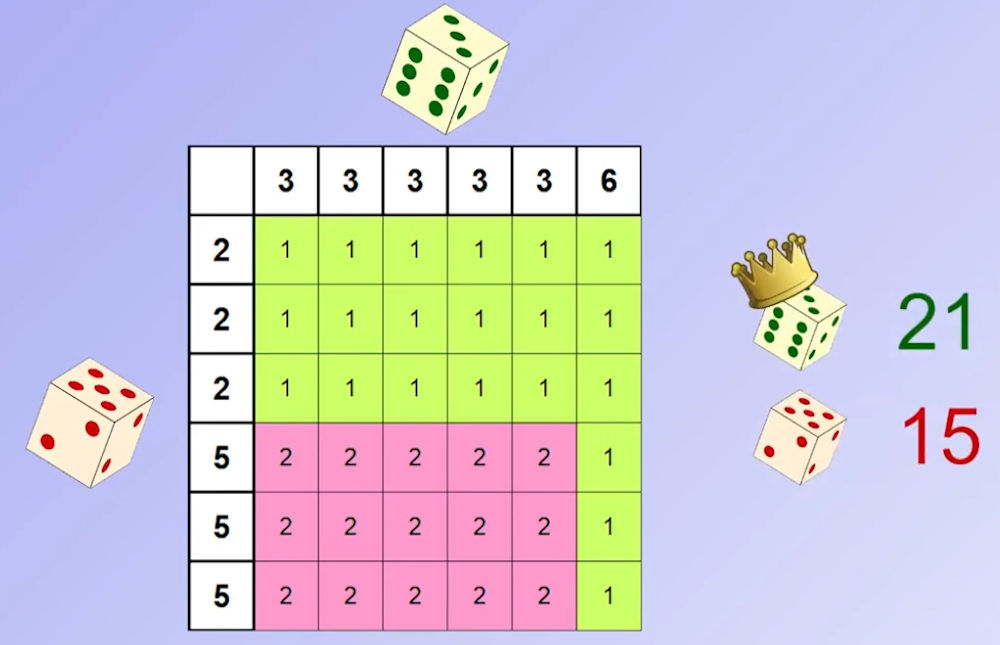 |
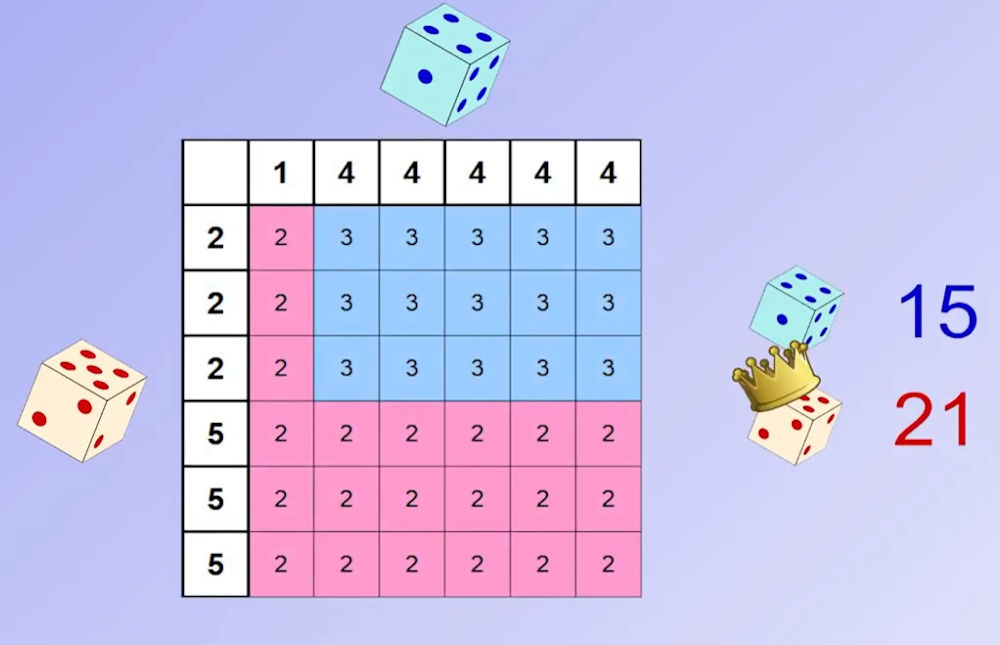 |
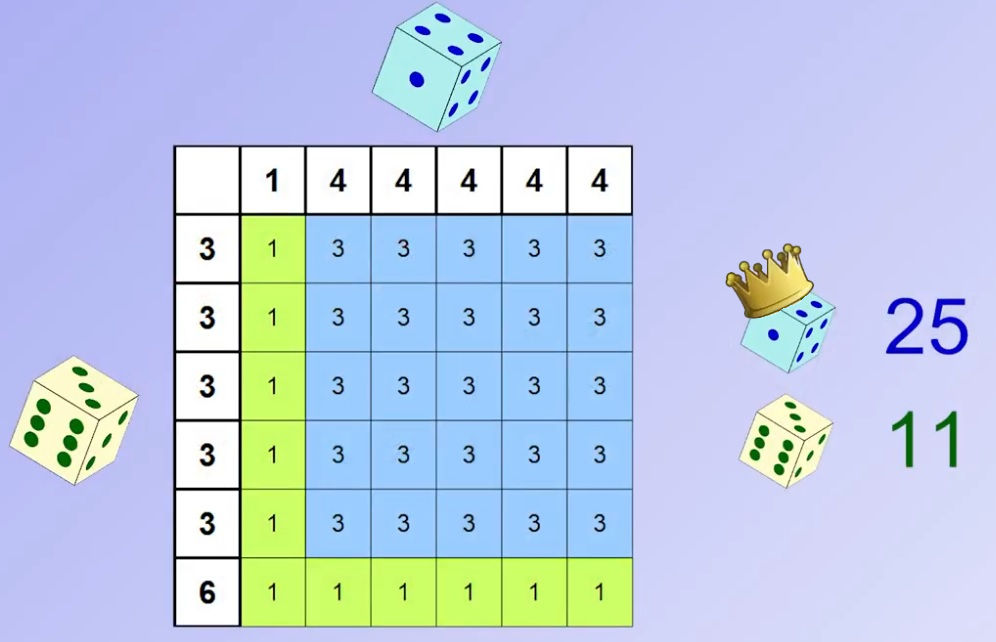 |
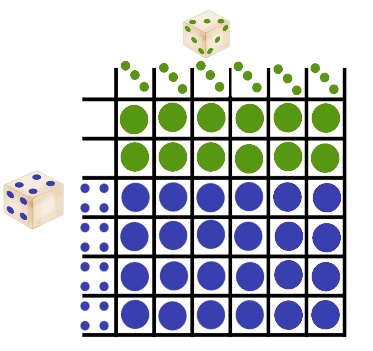
Mais si maintenant on lance deux fois chaque dé, il est peut probable que cela change le classement précédent. Et bien les 2 dés rouges deviennent meilleurs que les verts alors que seul, c’est le vert qui gagne !!!
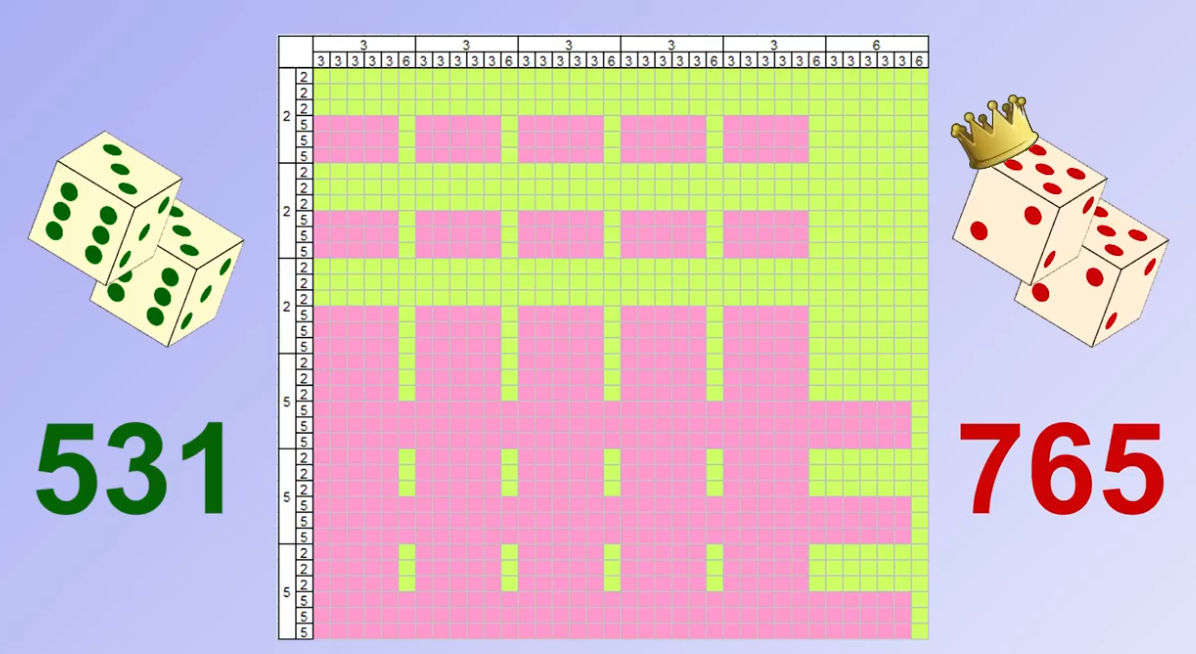
En fait tous les classements s’inversent à présent. Ils sont fous ces dés.
4°/ Le plus rapide :
Christophe, Sébastien et François font tous les jours la course pour se rendre de leur même immeuble jusqu’au collège. Il y a 201 jours de classe dans l’année. Christophe est arrivé au moins 134 fois avant Sébastien et se considère donc comme plus rapide que lui. Sébastien est arrivé au moins 134 fois avant François et se considère donc comme plus rapide que lui. Il est donc impossible que François soit arrivé au moins 134 fois avant Christophe, n’est-ce pas ?
Et bien si !!! Il n’est pas impossible que François se considère comme plus rapide que Christophe. Pour nous en persuader, nous pouvons imaginer les ordres d’arrivée suivants :
| 67 fois : Christophe, puis Sébastien puis François; 67 fois : Sébastien, puis François, puis Christophe ; 67 fois : François puis Christophe, puis Sébastien. |
134 fois : Christophe avant Sébastien |
C’est le paradoxe de Condorcet
2°/ Conjecture de FERMAT Puissance niéme :
Quel que soit a un nombre entier, il n’existe pas 2 autres entiers b et c tels que : an = bn + cn avec n >2
Fermat établira tout de même une preuve pour n = 4.
Plus tard, le suisse Leonhard Euler (1707 ; 1783) propose une démonstration pour n = 3. En 1828, l’allemand Peter Lejeune-Dirichlet (1805 ; 1859) la démontre pour n = 5, puis en 1840, Gabriel Lamé (1795 ; 1870) et Joseph Liouville (1809 ; 1882) pour n = 7.
La course folle après la conjecture de Fermat est lancée. Les plus grands mathématiciens et savants s’affrontent pour être le premier à venir à bout de cette étonnante conjecture à l’énoncé si simple mais dont la démonstration semble inaccessible. Il faut dire que des récompenses très appréciables sont promises. L’Académie des sciences de Paris promet une médaille d’or et une somme de 300 000 francs or. La Société royale de Göttingen offre 50 000$ (actuel) correspondant au prix Wolfskehl crée en 1908.
C’est en 1993 que la conjecture défraie la chronique. Les médias de toutes parts annoncent la fin de ce grand mythe des mathématiques, qui résistait depuis plus de 350 ans à toutes les démonstrations.
Le héros s’appelle Andrew Wiles, un anglais né à Cambridge en 1953. Sa mère, professeur de mathématiques l’initie très jeune au maniement des nombres.
C’est à l’âge de 10 ans qu’il tombe dans le piège de Fermat en empruntant à la bibliothèque un manuel d’histoire des mathématiques traitant de la conjecture de Fermat.
« Cela avait l’air si simple, et pourtant aucun des grands mathématiciens de l’histoire n’avait pu le résoudre. » Wiles
Pas si simple ! Wiles doit travailler dans le plus grand secret, le risque est trop grand, pense-t-il de se faire voler sa démonstration. Seuls ses plus proches collègues sont au courant de ses travaux. Il faudra à Wiles sept années d’isolement et de labeur pour arriver à bout, croyait-il, le 23 juin 1993 de la conjecture de Fermat. A l’Institut Isaac Newton de Cambridge, Il expose sa démonstration devant une assemblée de savants. L’idée de Wiles est remarquable, en passant par les courbes elliptiques, il unifie différentes branches des mathématiques pour prouver la conjecture de Fermat…
… Mais après plusieurs semaines, on s’aperçoit que sa preuve comporte une faille.

Andrew Wiles
Même si Wiles tente corriger son erreur, après ce revers, c’est le doute puis le désarroi qui l’emportent.
Quand le matin du lundi 19 septembre 1994, assis à son bureau, Wiles a de façon tout à fait inattendue une incroyable révélation. Il réalise ce qui empêche sa démonstration de fonctionner et se remet alors au travail.
En mai 1995, il publie la correction de sa démonstration qui est ensuite officiellement reconnue dans le monde scientifique. Celle-ci fait tout de même plus de 1000 pages. Fermat avait raison de dire qu’elle ne pouvait tenir dans sa marge !!!
Il reçoit alors un prix spécial par le congrès international des mathématiciens qui attribue habituellement la médaille Field (l’équivalent du prix Nobel en mathématiques), les 300 000 francs or de l’Académie des sciences, le prix Wolfskehl et surtout la fierté de voir la conjecture de Fermat changer de statut et de nom pour devenir le Théorème de Fermat-Wiles.

Cela marche avec n = 2. Il s’agit des triplets Pythagoriciens ( 3² + 4² = 5² par exemple).
Petit bonus : ce n’est pas la seule conjecture que Fermat a découvert. En voici une autre un peu plus simple car démontrée en 2006 par Gougam et Bagglio. 26 est le seul entier qui suit un carré 25 = 25² et précède un cube 27 = 33.
3°/ Duplicité du cube :
Soit un cube d’arête a. Il est impossible de trouver un autre cube d’arête b dont l’aire ou le volume soit le double du premier. En effet :
|
Arête |
Surface |
Volume |
|
a |
a² |
a3 |
|
b |
b² |
b3 |
| Un carré de côté b peut-il avoir une aire qui soit le double d’un carré de côté a ? | Un cube de côté b peut-il avoir un volume qui soit le double d’un cube de côté a ? |
| 2 x a² = b² 2 = b²/a² \sqrt{2} = b/a |
2 x a3 = b3 2 = b3/a3 \sqrt[3]{2}= b/a |
Or ni ni
ne sont des rationnels, donc ils ne peuvent s‘écrire comme tel c’est à dire sous la forme d’un rapport de 2 nombres entiers b/a.
4°/ Trisection d’un angle :
A l’aide d ‘une règle et d’un compas, il est impossible de partager un angle b donné, en 3 angles a égaux.
5°/ Le problème de Syracuse :
L’origine du problème n’est pas claire. Il semble que le mathématicien Lothar Collatz soit le premier à avoir, au début des années 1930, rencontré ce que l’on appelle, depuis, l’algorithme de Collatz ou le problème 3 N + 1. Vers 1950, Helmut Hasse, un ami de Collatz, introduisit le problème à l’Université de Syracuse (aux États-Unis et non en Sicile). C’est pour cette raison que le problème est maintenant connu sous le nom de conjoncture de Syracuse.
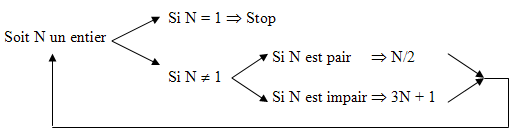
Recommencez de même avec le résultat… Vous arriverez fatalement à 1 au bout d’un nombre h (la hauteur du nombre initial) d’opérations. Mais quelle peut être la hauteur maximale ?
À l’heure actuelle, la conjoncture de Syracuse a été vérifiée pour tout nombre inférieur à mille milliards, mais on ne sait toujours pas prouver qu’elle est vraie pour tous les entiers !
Amusez-vous avec cette application SCRATCH :
6°/ La Conjecture de Goldbach : Info Wikipedia
En 1742, Christian Goldbach proposa à Leonhard Euler la conjecture suivante : « Tout nombre entier supérieur à 3 est somme de deux nombres premiers » (rem : à cette époque le nombre 1 est considéré comme premier).
Énoncé modernisé en : Tout nombre pair supérieur à 2 est la somme de deux nombres premiers.
Cette conjecture a fait l’objet de recherches par plusieurs théoriciens des nombres et a été vérifiée par ordinateur pour tous les nombres pairs jusqu’à 2.1018 à la date de novembre 2010. Voici un site qui propose de décomposer les nombres.
Mais aujourd’hui encore personne n’a pu prouver qu’elle était valable pour TOUS les entiers !!
Le site WIMS de l’université de Nice propose de calculer simplement la décomposition en sommes de 2 nombres premiers, pour un nombre de votre choix.
7°/ Le Problème de Catalan :
En 1844, Catalan proposa l’énoncé suivant: les seuls puissances parfaites consécutives sont 8 et 9. Autrement dit l’équation xp – yq = 1, avec x, y, p et q entiers n’admet comme solution que le couple (8,9). On sait depuis 20 ans qu’il n’y a en tout cas qu’un nombre fini de solutions, on connait également la borne supérieure de ces solutions, mais elle est si élevée que même à l’aide des ordinateurs les plus puissants, on n’a jamais pu trouver d’autres solutions à l’équation. Apparemment la conjecture de Catalan a de beaux jours devant elle…
8°/ Elkies contredit Euler :
Mais même les plus grands mathématiciens peuvent se tromper dans leurs conjectures: ainsi Leonhard Euler (1707/1783) qui avait prévu que la somme de trois bicarrés ne pouvait être un bicarré, c’est-à-dire que l’équation a4 + b4 + c4 =d4 n’admet aucune solution avec a,b,c,d entiers naturels. Or il se trompait !! Car l’américain N. Elkies a trouvé une solution à cette équation en 1988 !! Et on sait de plus qu’il n’y a qu’une solution avec d inférieur à 1 million.
Cette solution est a = 95800 b = 217519 c = 414560 et d = 422481.
9°/ Le paradoxe de Zénon d’Elée : La flèche
Zénon se tient à huit mètres d’un arbre, et tire une flèche sur cet arbre. Avant que le flèche puisse atteindre l’arbre, elle doit traverser la première moitié des huit mètres. Il faut un certain temps, non nul, à cette flèche pour se déplacer sur cette distance. Ensuite, il lui reste encore quatre mètres à parcourir, dont elle accomplit d’abord la moitié, deux mètres, ce qui lui prend un certain temps. Puis la pierre avance d’un mètre de plus, progresse après d’un demi-mètre et encore d’un quart, et ainsi de suite ad infinitum et à chaque fois avec un temps non nul.
Zénon en conclut que la flèche ne pourra pas frapper l’arbre, puisqu’il faudrait pour cela que soit franchie effectivement une série infinie d’étapes, ce qui est impossible. Le paradoxe se résout en soutenant que le mouvement est continu ; le fait qu’il soit divisible à l’infini ne le rend pas impossible pour autant. De plus, en analyse moderne, le paradoxe est résolu en utilisant fondamentalement le fait qu’une série infinie de nombres strictement positifs peut converger vers un résultat fini.
Ce paradoxe dit de « la dichotomie » c’est à dire division par deux veut montrer l’impossibilité du mouvement. Il tend à mettre en doute la vérité par un raisonnement logique. Par ce paradoxe on peut en déduire que le mouvement ne peut être découpé en une infinité de morceaux. Cependant et les mathématiques nous le confirment si on fait la somme (infinie) de toutes les distances du problème on trouve 1 : 1/2+1/4+1/8+…
La limite de cette suite vaut 1. Donc on atteindra bien ce point. Mais une limite est ce vers quoi on tend sans jamais l’atteindre…
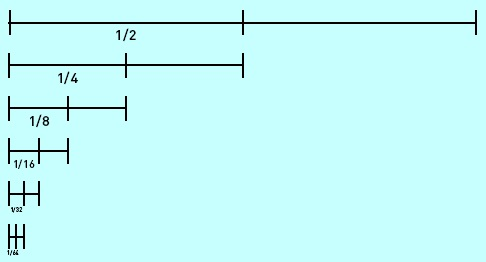 |
\lim_{n \to \infty }(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+..\frac{1}{2^{n}})= 1 |
10°/ L’avocat :
Le sophiste Protagoras avait convenu avec un de ses élèves Euathlus, un étudiant pauvre, qu’il lui enseignerait le droit à la condition qu’Euathlus lui payât cet enseignement dès qu’il aurait gagné son premier procès. Le jeune homme suivit ses leçons, puis finalement devient avocat. Il attendit alors ses premiers clients qui ne virent pas.
Protagoras s’impatienta et décida alors de réclamer à son ancien élève la somme qu’il lui devait. Il l’assigna donc devant les tribunaux.
– Ainsi raisonna Protagoras:
« Ou je gagne le procès, ou tu le gagnes. Si je gagne, tu me paies en exécution du jugement du tribunal. Si tu gagnes, tu me paies d’après notre convention. Dans les deux cas je serai payé ».
– « Pas du tout », répliqua Euathlus. « Si je gagne, je n’ai pas à te payer, d’après le jugement du tribunal. Si tu gagnes je n’ai pas à te payer d’après notre convention. Dans les deux cas je n’ai pas à te payer. »
Alors que va choisir le tribunal?
Les 2 personnages raisonnent correctement.
Voici comment le tribunal pourrait agir pour dissiper ce paradoxe:
D’abord, le juge décide de faire gagner Euathlus. Il aura ainsi remporté son premier procès.
Ensuite, Protagoras pourra intenter un nouveau procès et pourra se faire rembourser son dû sans créer un nouveau paradoxe.
11°/ Le segment qui se voulait aussi grand qu’une droite… :
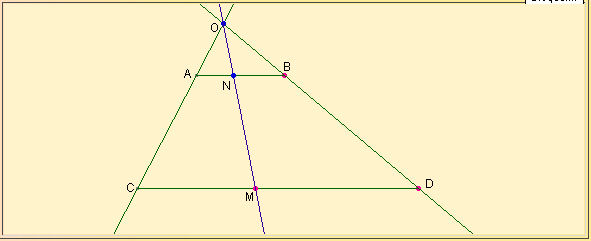
A chaque point N de [AB], correspond un point unique M de [CD].
Et à chaque point M de [CD] correspond un point unique N de [AB].
Chaque point de chaque segment a son correspondant sur l’autre.
Les deux segments [AB] et [CD] ont donc le même nombre de points mais pas la même longueur…
12/ \sqrt{2} = 2 :
Soit un triangle rectangle et isocèle de côté 1 et d’hypoténuse \sqrt{1^{2} + 1^{2}} = \sqrt{2}
La somme des longueurs des 2 côtés de l’angle droit est 1 + 1 = 2.
Si nous construisons une ligne brisée avec des gradins en angle droit comme sur la figure ci-dessous, il est facile de conclure que sa longueur est toujours égale à 2 (les segments verticaux mis bout à bout ont une longueur de 1 et les horizontaux mis bout à bout ont aussi une longueur de 1).
En réitérant le procédé, nous avons toujours une ligne brisée de longueur 2.
Continuons indéfiniment à augmenter le nombre de gradins, nous obtenons une suite de lignes brisées qui se rapprochent de plus en plus de l’hypoténuse du triangle rectangle. On a bien envie de penser que la ligne brisée se confondra à la fin avec l’hypoténuse et donc que sa longueur sera celle de l’hypoténuse donc =2 !!
Explication :
La ligne brisée ne sera pas confondue avec l’hypoténuse du triangle. Elle n’a pas tous ses points sur l’hypoténuse. L’ensemble des points communs à la ligne brisée et l’hypoténuse est un ensemble dénombrable de points et il existe des points intermédiaires non communs à la ligne brisée et l’hypoténuse.
La ligne brisée a une longueur constante 2 et l’hypoténuse a une longueur de .
13°/ Factorielles et carrés :
Existe-t-il un couple d’entiers p > 7 et q tels que la factorielle de p, plus un soit égale à q ?
p! + 1 = q² ?
Il est connu que 4! +1 = 25 = 5²
5! + 1 = 121 = 11²
7! + 1 = 5041 = 71²
On ne connaît pas d’autre solution.
14°/ Fractions égyptiennes :
Un entier n > 1 étant donné, existe-t-il des entiers x, y et z tels que 4/n = 1/x + 1/y + 1/z ?
Les fractions 1/x, 1/y et 1/z dont le numérateur est égal à 1 et le dénominateur est un entier naturel positif, sont appelées fractions égyptiennes.
4/n doit donc être la somme de trois fractions égyptiennes.
On connaît des solutions chaque fois que n est différent de 24k+1
Par exemple, pour n=7, on a : 4/7 = 1/3 + 1/6 + 1/14.
Mais on ne sait pas montrer que le problème est possible pour tout n.
15°/ Équations Diophantiennes :
Il existe 4 nombres a, b, c et d qui vérifient les équations diophantiennes suivantes :
a² + b² = c² + d²
a3 + b3 = c3 + d3
a4 + b4 = c4 + d4
Mais on ne connaît pas de relation similaire pour a5 + b5 = c5 + d5
16°/ Côtés et segments remarquables du triangle :
On sait résoudre un joli problème dans lequel 17 longueurs dans un triangle ABC sont toutes des nombres entiers : les trois côtés, les trois hauteurs (hA, hB ,hC), les trois bissectrices intérieures (AA’, BB’, CC’) et les trois bissectrices extérieures (AA’’, BB’’, CC’’) , le rayon R du cercle circonscrit et le rayon r du cercle inscrit et les trois rayons des cercles exinscrits (rA, rB ,rC) (cité par Jean Moreau de Saint Martin).
AB = 148622918043600 BC = 160847313900000 AC = 185939494868400
hA = 154413421344000 hB = 142678001321856 hC = 123423876576000
rA = 115810066008000 rB = 132109260483200 rC = 185778647554500
AA’ = 156251676360000 BB’ = 145764785004300 CC’ = 123594942240000
AA’’ = 1009626216480000 BB’’ = 696990236342400 CC’’ = 2346677653320000
r = 46324026403200 R = 96843486910625.
Un autre problème d’énoncé plus simple n’a toujours pas de solution à ce jour : existe-t-il un triangle dont les côtés, les médianes et l’aire s’expriment avec des nombres entiers ?
17°/ Les distances d’un point aux sommets d’un carré :
On considère dans le plan un carré de côté unité. Existe-t-il un point du plan dont les distances aux quatre sommets du carré s’expriment sous la forme de nombres rationnels ?
En d’autres termes existe-t-il un carré de côté n entier tel qu’il existe un point du plan situé à des distances entières des quatre sommets du carré ? Aucune solution n’existe à ce jour.
On peut rapprocher cet énoncé d’un problème analogue sur la sphère, non résolu à notre connaissance : peut-on tracer quatre cercles de rayons rationnels sur une sphère de rayon unité tels qu’ils soient tangents deux à deux ?
18°/ La brique parfaite d’Euler :
La brique parfaite d’Euler est un parallélépipède rectangle dont les côtés a, b et c, les diagonales des faces,
et
et la diagonale principale qui joint deux sommets opposés
sont tous des nombres entiers. Aucun exemple de cette brique parfaite n’existe à ce jour.
19°/ Le paradoxe d’Epiménide le Crétois :
Un paradoxe dû à Epiménide le Crétois (Vie siècle av. J.C.). C’est un syllogisme , basé sur le raisonnement logique.
Voici l’énoncé :
« Tous les Crétois sont des menteurs.
Si tous les Crétois sont des menteurs, alors Epiménide le Crétois est un menteur.
Si Epiménide est un menteur, ce qu’il dit est faux, donc il ne ment pas et ce qu’il dit est vrai. »
Donc comme Epiménide dit vrai, tous les Crétois sont des menteurs. Mais comme Epiménide est un Crétois, c’est un menteur.
Et on retombe sur un cercle vicieux.
20°/ Quelques sophismes :
» Un cheval bon marché est rare.
Or ce qui est rare est cher
Donc un cheval bon marché est cher. «
Cette conclusion est contradictoire, pourtant chacune des phrases du raisonnement paraît correcte. Pourquoi parvient-on à un tel résultat ?
On peut ajouter une dose d’humour et le formuler autrement :
» Plus il y a de gruyère, plus il y a de trous.
Or plus il y a de trous, moins il y a de gruyère
Donc plus il y a de gruyère, moins il y a de gruyère .. »
Il existe tout plein de belles phrases qui se contredisent de façon très élégante :
Il est interdit d’interdire.
Toutes les règles ont des exceptions.
Lu sur un badge : Interdisons les badges.
Un graffiti disait : A bas les graffitis.
21°/ Le barbier barbant :
Sur l’enseigne d’un barbier est inscrit :
» Je rase tous les hommes du village qui ne se rasent pas eux-mêmes, et seulement ceux-là. »
Alors d’après vous qui rase le barbier?
On voit bien le paradoxe. En effet, si le barbier se rase lui-même, alors d’après ce qu’il dit, il ne peut pas se raser. Au contraire s’il ne se rase pas, il doit alors se raser pour respecter son enseigne.
Et là, il y a paradoxe. Donc la condition que définit le barbier crée une contradiction. On ne peut que conclure qu’un barbier qui prétend cet axiome ne peut exister.
22°/ Le paradoxe de Zénon d’Elée : Achille et la tortue
Pour une raison maintenant oubliée dans les brumes du temps, une course avait été organisée entre le héros Achille et une tortue.
Le premier se déplaçant 10 fois plus vite que la seconde, celle-ci démarra avec 100 m d’avance pour équilibrer les chances des deux concurrents.
La première chose à faire pour Achille fût de combler son retard en se rendant à l’endroit de départ de la tortue qui, pendant ce laps de temps, s’était déplacée. Achille dut donc combler ce nouvel handicap alors que la tortue, bien que d’une lenteur désespérante, continuait inexorablement sa route, créant ainsi un handicap supplémentaire…
Battu et furieux, Achille exigea une revanche mais rien n’y fit, ni la longueur de la course, ni la vitesse de déplacement d’Achille.
En effet, aussi petits que soient les handicaps successifs créés par la tortue, Achille mettait toujours un certain temps pour combler chacun d’entre eux et, malgré tous ses efforts, il ne put jamais rattraper la tortue!
Vitesse d’Achille : 10m.s-1 dA = Distance parcourue par Achille TA = temps de corse d’Achille
Vitesse de la tortue : 1m.s-1 dt = Distance parcourue par la tortue Tt = temps de corse de la tortue
| dA | TA = dA/10 = Tt | dt = Tt |
| 100m | 10s | 10m |
| 10m | 1s | 1m |
| 1m | 1/10s | 1/10m |
| 1/10m | 1/100s | 1/100m |

On le voit bien, dA diminue d’un facteur 10 mais n’est jamais égal à zéro, tout comme TA et Tt.
Par conséquent, le nombre de secondes qui s’écoulent avant qu’Achille ne rattrape la tortue est :
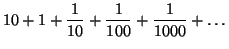
On obtient une somme comportant une infinité de termes. Ce que Zénon d’Elée n’avait pas prévu, c’est que cette somme infinie possède une valeur finie. Les règles sur les séries géométriques montrent en effet sans peine que la somme précédente fait 11s et 1/9.
La manipulation des sommes infinies (on parle de séries) a très longtemps posé des problèmes conceptuels et philosophiques aux mathématiciens. Le cours de Cauchy à l’Ecole Polytechnique en 1820, pourtant un modèle pour l’époque, comporte encore des erreurs à ce sujet. Il faudra attendre la fin du XIXè s., et les travaux de Karl Weierstrass, le législateur de l’analyse, pour que les règles soient clairement établies.
23°/ Paradoxe de Socrate et Platon :
Socrate et Platon sont des philosophes grec du V? siècle av. J.-C.
Voici un joli paradoxe :
Socrate : Ce que dit Platon est faux.
Platon : Ce que dit Socrate est vrai.
Si Socrate dit vrai, alors ce que dit Platon est faux. Il faut prendre le contraire de ce que dit Platon, en l’occurrence que Socrate ment, ce qui est le contraire de l’affirmation de départ.
Si par contre, ce que dit Platon est vrai, alors Socrate dit la vérité, c’est-à-dire que Platon ment, ce qui est aussi contraire à l’affirmation de départ.
Voyons les 2 autres cas :
Si Socrate ment, alors ce que dit Platon est vrai, c’est-à-dire que Socrate dit la vérité, ce qui est encore le contraire de l’affirmation de départ.
Si par contre, c’est Platon qui ment, alors Socrate ment aussi, c’est-à-dire que Platon dit la vérité, ce qui est toujours contraire à l’affirmation de départ.
Finalement les deux phrases ne peuvent être correctes en même temps. Cela s’appelle un paradoxe.
24°/ Les nombres de Ramsey : Info Wikipedia
Théorème de Ramsey (fini) : Pour tout entier c et toute suite d’entiers (n1, n2, … , nc), il existe un entier N tel que pour toute coloration en c couleurs du graphe complet KN d’ordre N, il existe une couleur i et un sous-graphe complet de KN d’ordre ni qui soit monochromatique de couleur i.
En clair, si on prend un nombre de points N et qu’on les relies par un trait de couleur qui est soit rouge ou soit bleu, peut-on trouver un groupe de points qui est relié par la même couleur.
Par exemple :
| Pour ces 5 points il y a 3 points qui sont reliés en bleu. | Ici il n’y a aucun points qui sont reliés de la même couleur. |
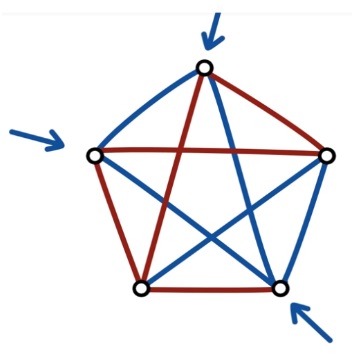 |
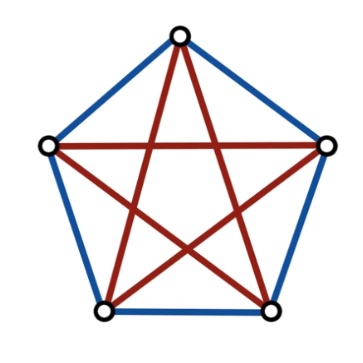 |
r représente le nombre de sommet du polygone bleu et s représente le nombre de sommet du polygone rouge.
R(4,3) = 9 indique qu’il faut 9 points pour faire des quadrilatères bleus (4 points) et des triangles rouges (3 points) ou vide et versa.
Le tableau ci-dessous montre que l’on est pas capable de déterminer des valeurs exactes pour la plupart des problèmes : 43 points < R(5,5) < 49 points, nous n’avons que des encadrements et pas de valeur exactes.
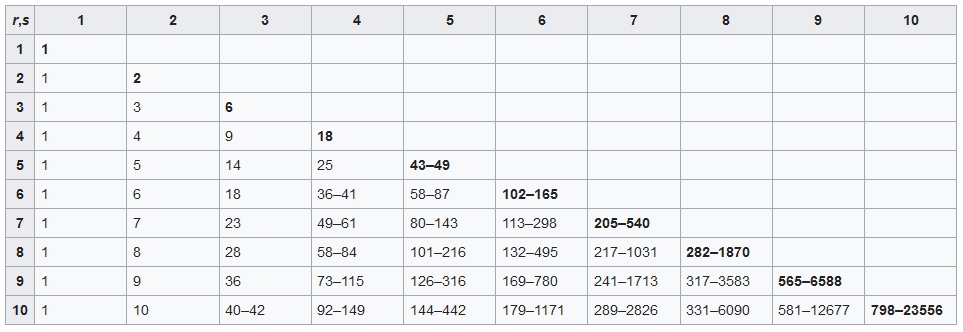
25°/ Les nombres de Lychrel :
Un nombre palindrome est un nombre qui peut se lire de droite à gauche, comme 272 = 272.
Il est surprenant de remarquer que si on ajoute n’importe quel nombre et sont renversé (le même nombre écrit à l’envers), on obtient un nombre palindrome.
par exemple : 143 + 341 = 484
On peut le faire en plusieurs étapes : 153 + 351 = 504 puis 504 + 405 = 909
Mais existe t’il des nombres qui ne respectent pas cette propriété ? On les appelle des nombre de Lychrels et on ne sait pas s’il en existe. On a des soupçons sur le nombre 196 mais sans être capable de le prouver.
La liste des nombres de Lychrel soupçonnés sur OEIS.
Pour tester les possibles nombres de Lychrel.
26°/ Le nombre chromatique du plan :
Peut-on colorier une feuille de papier avec un nombre minimal de couleur pour qu’un segment ne puisse pas relier 2 zone de la même couleur ?
| Ici ce n’est pas possible. | Ici le segment ne pourra jamais atteindre 2 zone de la même couleur. |
 |
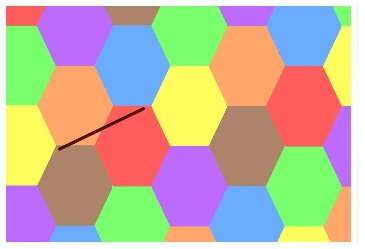 |
La réponse serait un pavage hexagonal avec un nombre ce couleur compris entre 4 et 7. Pas plus de précision.
Un excellent article sur le blog d’eljj.
27°/ Persistance multiplicative :
Prenons un nombre entier : 53
Multiplions ces 2 chiffres : 5 x 3 = 15
Continuons : 1 x 5 = 5
Nous arrivons à un nombre composé d’un seul chiffre en cela en 3 étapes. La persistance multiplicative de 53 est donc de 3.
Quel est le nombre qui a la plus grande persistance multiplicative ?
Pour le moment on a trouver les nombres 277 777 788 888 899 et 27 777 789 999 999 999 donc la persistance multiplicative est de 11. Mais on ne sait pas si on peut dépasser 11.
Une appli pour calculer la persistance d’un nombre.
28°/ Paradoxe des anniversaires et Rubik’s cube :
Combien faut-il de personnes pour que l’on ait 50 % de chance de trouver deux personnes qui ont la même date d’anniversaire ?
La logique voudrait qu’il en faille beaucoup, mais …
Avec 23 personnes on aura 50,73 % de chance, ce qui n’est vraiment pas beaucoup convenons-en.
A partir de 60 personnes on aura 99,81 %
La preuve :
Avec 23 personnes, le premier a 22 possibilités d’avoir un anniversaire commun avec quelqu’un.
Le 2ième a 21 possibilités d’avoir un anniversaire commun avec quelqu’un.
Le 3ième a 20 possibilités d’avoir un anniversaire commun avec quelqu’un.
…………..
Le 22ième a 1 possibilité d’avoir un anniversaire commun avec quelqu’un.
Le nombre d’anniversaires commun = 22 + 21 + 20 + … + 2 + 1 = 23 x 11 = n(n+1)/2 = (23 + 22)/2 = 253 fois la même question a posée : as-tu le même anniversaire que moi.
La démonstration sera plus simple si on compte la probabilité que les 23 personnes n’aient pas le même anniversaire.
S’il y a 2 personnes elles auront 1 chance sur 365 d’avoir le même anniversaire et donc 364/365 de ne pas avoir le même anniversaire.
S’il y a 3 personnes, une personne aura 364/365 chance de ne pas avoir le même anniversaire avec la deuxième et 363/365 avec la troisième, c’est à dire \frac{364}{365}\times \frac{363}{365}
Et ainsi de suite. Le tableur Excel suivant donne tous les résultats (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page Excel ci-dessous pour l’ouvrir dans Microsoft Office Online).
On se rend bien compte que c’est à partir de 23 personnes que l’on a 50% de chance qu’il y ait 2 personnes ayant le même anniversaire.
Il est interressant de remarquer que Excel atteint ses limites à partir de 83 personnes car il affiche 100% de chance, ce qui est impossible !!!
Rubik’s cube : même jeu avec le Rubik’s cube
Il y a 43×1018 de combinaisons possibles au Rubik’s cube (exactement 43 252 003 274 489 856 000), en le tenant de la même façon, c’est-à-dire la face rouge vers le haut par exemple.
Combien faut-il de personnes qui mélange un Rubik’s cube, pour qui l’on ait la même combinaison ?
Sur 365 jours il faut 23 personnes pour qu’il y ait 50 % de chance que 2 personnes aient le même anniversaire.
Sur 43×1018 combinaisons possibles au Rubik’s cube il faut 7 743 000 000 personnes pour qu’il y ait 50 % de chance que 2 personnes aient la même combinaison. C’est-à-dire à peu près la taille de la population de la terre.
Petite remarque : le nombre de dieu du Rubik’s cube est 20. C’est le nombre de mouvement minimum qu’il faut faire pour résoudre n’importe quel Rubik’s cube.
29°/ Le plus court chemin est-il la ligne droite ?
Peut-on aller de l’Espagne jusqu’en Nouvelle Zélande en bateau et en ligne droite ?
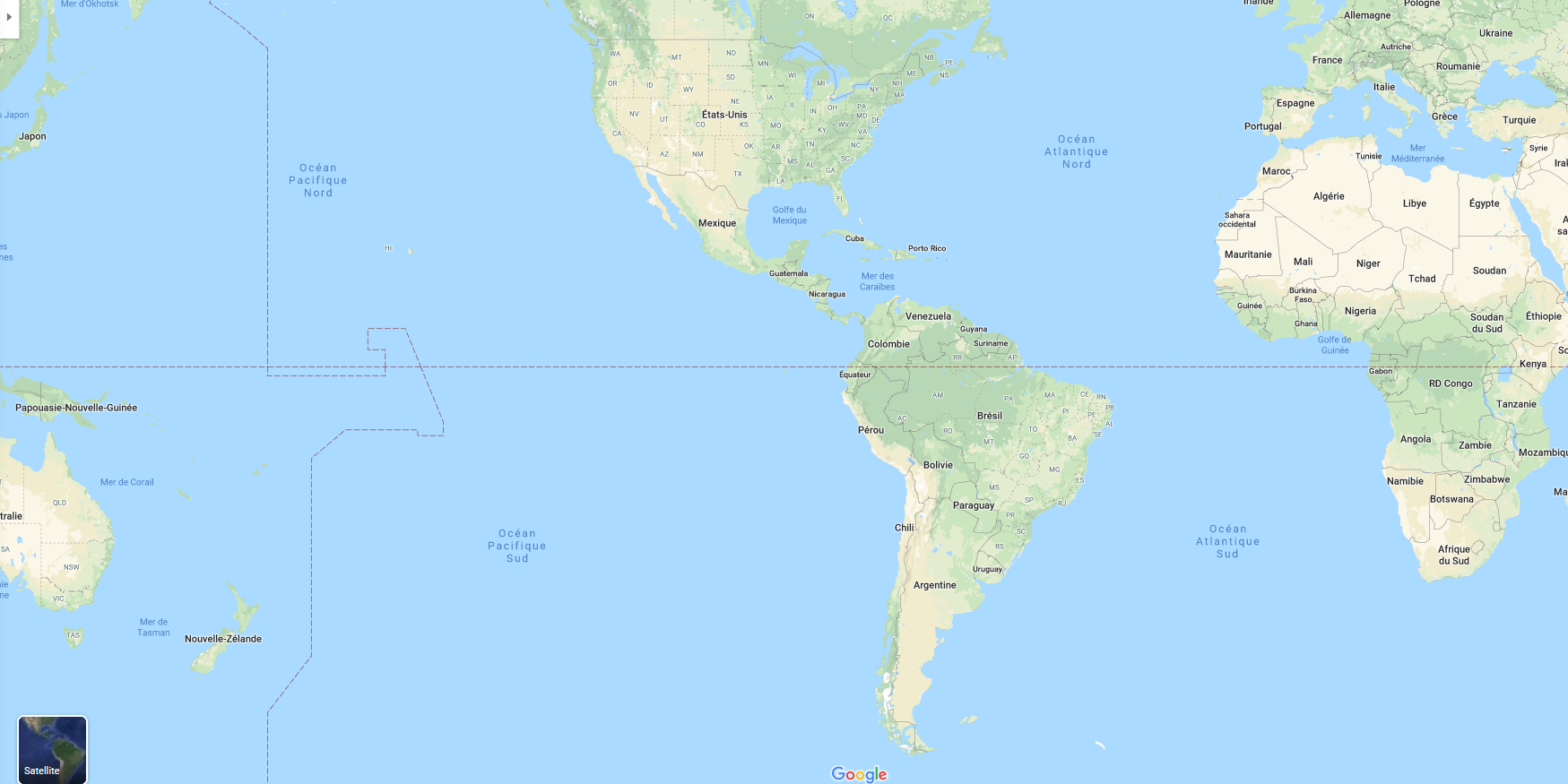
Voilà ce que cela donne avec Google map.
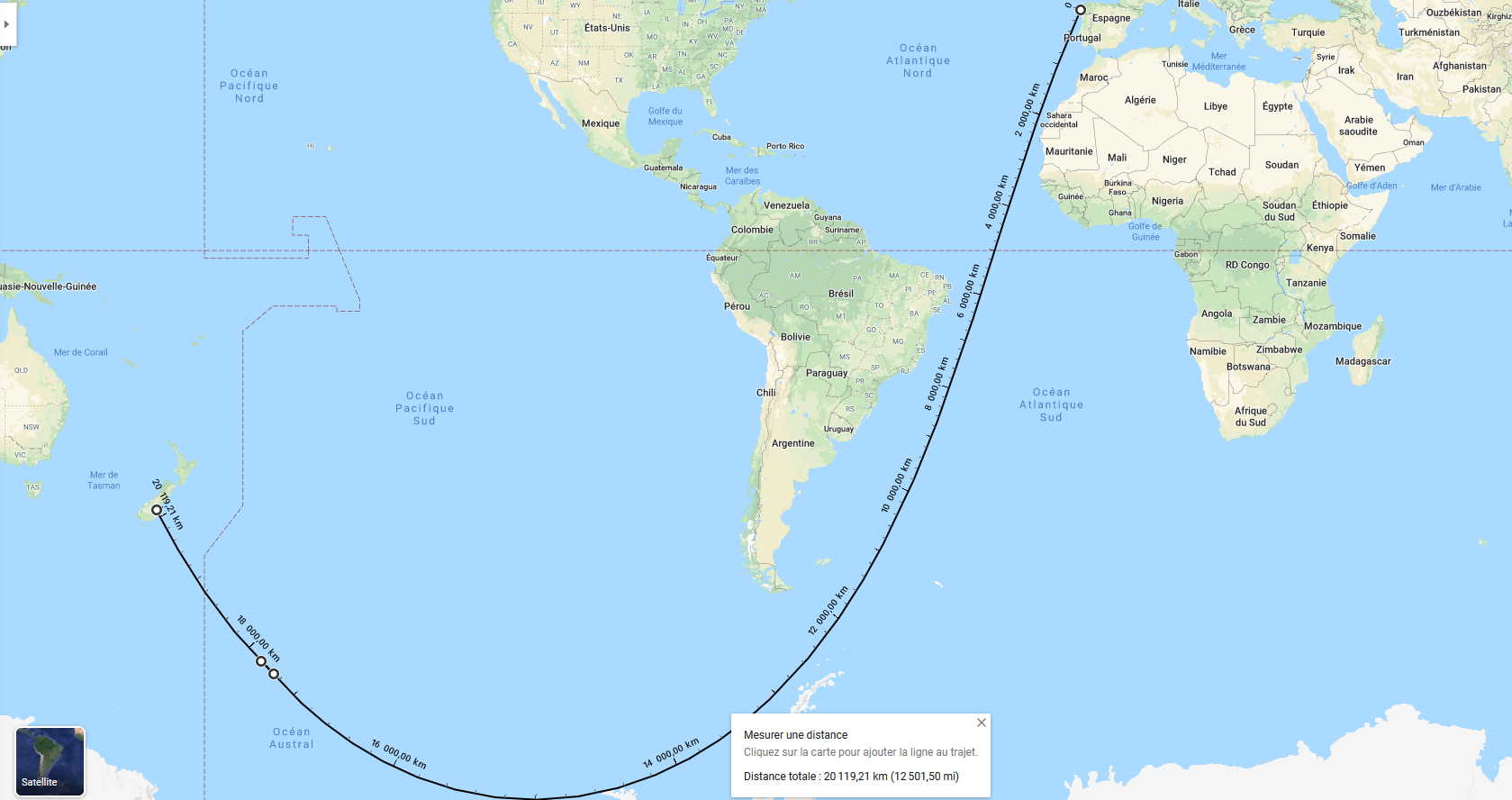
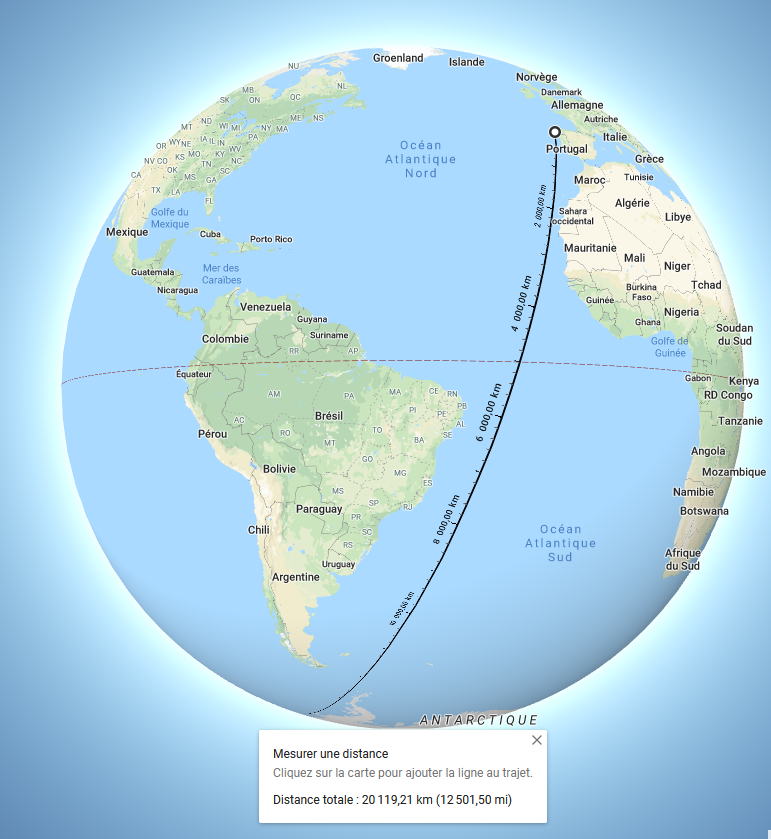
En fait ce trajet est parfaitement rectiligne du fait de la courbure de la terre. La preuve toujours avec Google map mais en mode planète.
 |
 |
De la même manière on peut aller de l’Inde aux États Unis en allant tout droit :
Pour jouer, voici un petit exercice. Depuis Calais, dans le nord de la France, et en partant vers le nord sur la mer, quelle est la première terre que l’on rencontrera ?
Et bien ce sera l’Antarctique, c’est-à-dire le pôle sud !!! On passera par le pôle nord et on fera le tour de la terre.
Encore plus fou : Voici les distances entre les villes de Paris, New York, Le Cap en Afrique du Sud et Buenos Aires (Voici un site pour obtenir ces distances : https://fr.distance.to/).
| Paris | New York | Le Cap | Buenos Aires | |
| Paris | 5790 km |
9345 km | 11054 km | |
| New York | 5790 km |
12568 km | 8530 km | |
| Le Cap | 9345 km | 12568 km | 6870 km | |
| Buenos Aires | 11054 km | 8530 km | 6870 km |
Plaçons-les à l’aide d’un compas sur une carte. Commençons par placer Paris, New York, Le Cap.
Et bien il est impossible de placer cette 4ième ville sur un plan, toujours à cause de la courbure de la terre. Notre construction avec des cercles utilise la géométrie Euclidienne qui est bien entendue inutilisable dans la géométrie sphérique que l’on doit utiliser pour se déplacer sur la terre.
30°/ \pi = 4 ou même 2 :
Partons d’un carré de 1 unité de côté. Replions ensuite un chaque coin vers l’intérieur. Ainsi de suite un nombre de fois infinie pour arriver à un cercle.
On peut conclure que la limite de l’aire de la dernière figure est égale au périmètre du cercle de diamètre 1 unité.
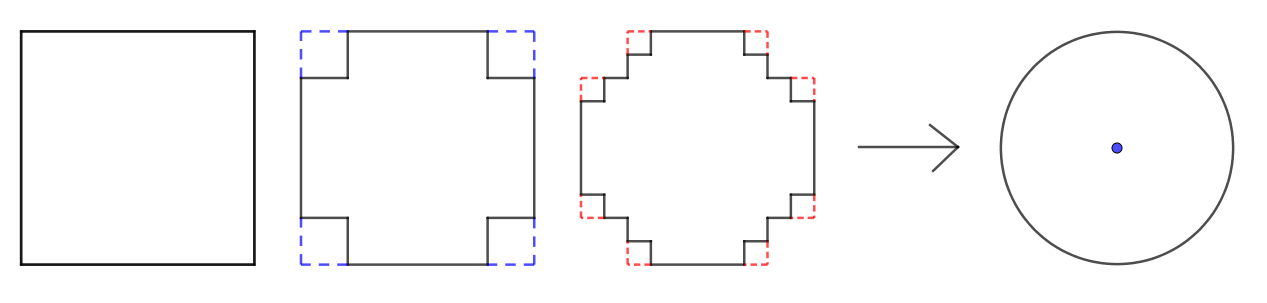
On remarque que chaque coin en pointillé a la même longueur que le coin intérieur, et que donc le périmètre ne change pas.
Si le raisonnement est correct : Perimetre_{cercle}=2\pi R = \pi D = \pi = Perimetre_{carre}=4 \times 1 = 4 \ unites
Donc : \pi = 4
Mais on peut aussi prouver que \pi = 2
Traçons un demi-cercle de rayon 1 unité.
Perimetre_{1/2 cercle \ bleu}=\pi R = \pi \times 1 = \pi unitePerimetre_{1/2 cercle \ vert}=\pi \times 0,5 = \frac{\pi }{2} unites donc : 2 \ Perimetres_{1/2 cercle \ vert}=\pi \ unite
Perimetre_{1/2 cercle \ jaune}=\pi \times 0,25 = \frac{\pi }{4} unites donc : 4 \ Perimetres_{1/2 cercle \ jaune}=\pi \ unite
En répettant ainsi, la somme de tous les 1/2 cercles sera donc toujours égale à \pi . Or la limite de la somme des 1/2 cercles est égale au diamètre de 2 unités.
Nous venons de démontrer que \pi = 2.
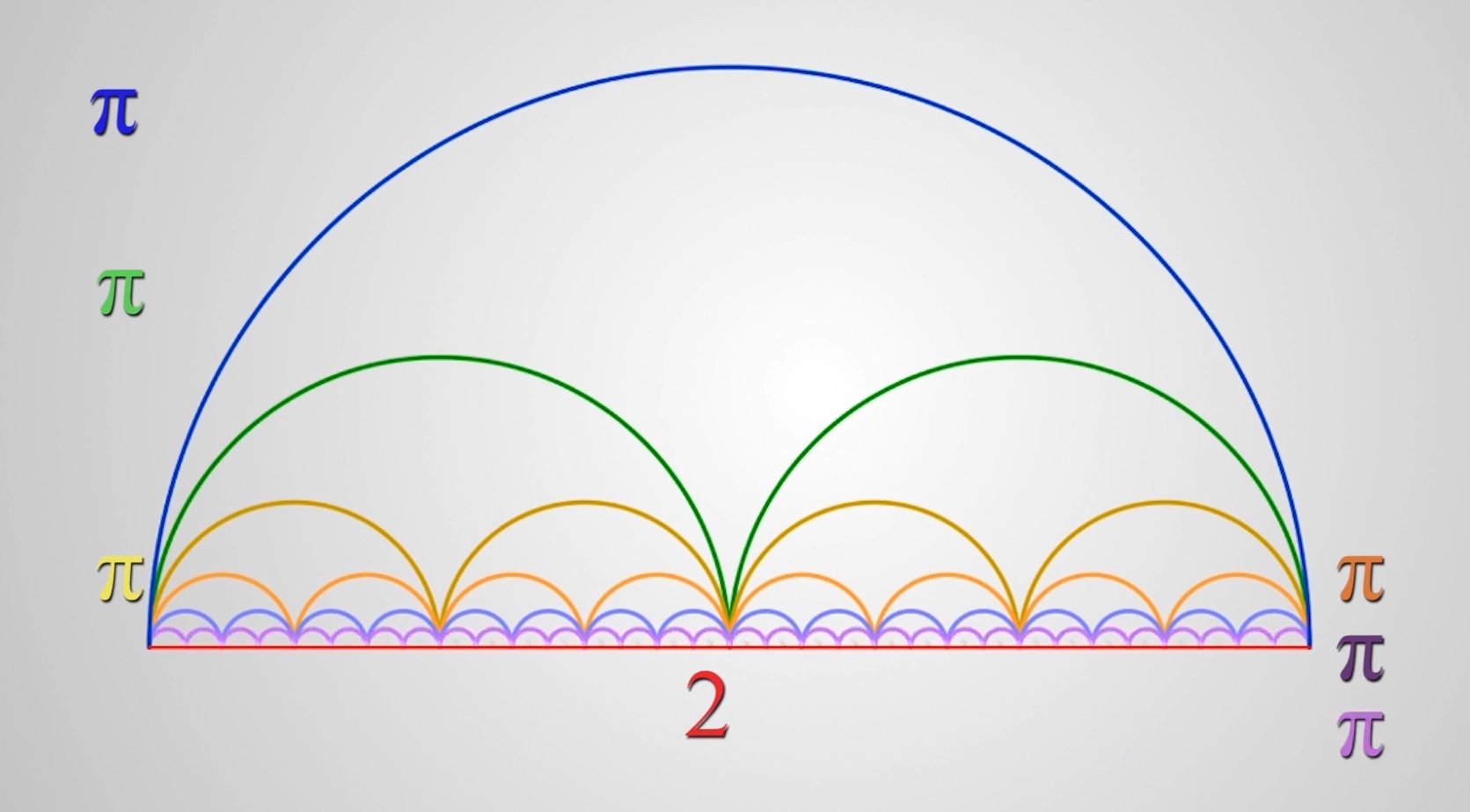
Bien évidemment \pi n’est égal ni à 4 ni à 2. Cette grossière erreur vient du fait que on déduit de chacune des deux expériences précédentes, que la limite des découpages successifs, qui est est égale à \pi dans chaque cas, est égale à la longueur de la limite des figures de départ, c’est à dire 4 ou 2.
Or ces découpages sont caractérisés par une fonction discontinue où la notion de limite n’a aucun sens.
31°/ Les bœufs d’Helios :
Voici un problème proposé par Archimède de Syracuse (Italie) à ses confrères d’Égypte :
« Le soleil (c’était alors un dieu) possédait un troupeau de taureaux et de vaches, dont une partie était blanche, une partie noire, une partie rose, et la quatrième partie jaune. Parmi les taureaux, le nombre de ceux qui étaient blancs dépassait le nombre des jaunes de la moitié plus un tiers du nombre des taureaux noirs. Le nombre des taureaux noirs dépassait le nombre des taureaux jaunes d’un quart plus un cinquième du nombre des taureaux roses. Enfin le nombre des taureaux roses dépassait celui des jaunes d’un sixième plus un septième du nombre des taureaux blancs.
Parmi les vaches, le nombre des blanches était égal au tiers augmenté du quart du nombre total des bovins noirs. Le nombre des vaches noires, au quart augmenté du cinquième du nombre total des bovins roses. Le nombre des vaches roses, au cinquième augmenté du sixième du nombre total des bovins jaunes. Enfin le nombre des vaches brunes était égal à un sixième plus un septième du nombre total des bovins. »
Il s’agit de dénombrer ce troupeau.
C’est un problème d’analyse diophantienne qui fut découvert en 1773 par Gotthold Lessing dans un manuscrit grec et attribué à Archimède. Ce problème ne fut résolu qu’en 1880 par A. Amthor qui en donna une solution exacte sous forme de produit d’irrationnels. La solution fait intervenir de très grands nombres, que des ordinateurs peuvent aujourd’hui écrire et fait intervenir l’équation de Pell-Fermat .
 |
Voici un résumé des 7 équations à 8 inconnues. Il manque une équation pour obtenir une solution unique, et si elle existe, alors il y en aura une infinité.
En effet, la solution la plus simple donne un troupeau de 7,76 x 10206544 animaux !!! Il est plus que probable qu’Archimède n’a pas résolu ce problème. On se demande même si, taquin, il ne voulait pas mettre en difficulté ses collègues. |
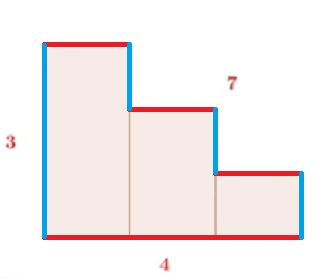
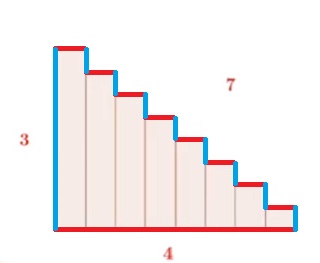
32°/ Pythagore nous aurait menti ?
Calculons la hauteur des marches et contremarches d’un escalier de base 4 unités et de hauteur 3 unités.
 |
 |
 |
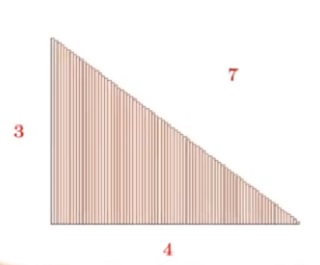 |
| La longueur des marches rouges est équivalente à la base de 4 unités, et la longueur des contremarches à la longueur bleue de 3 unités. On obtient 7 unités. | Avec 3 marches on obtient le même résultats. | Ainsi qu’avec 8 marches. La longueur des marches rouges et des contremarches bleues ne dépend pas du nombre de marches total. |
Si l’escalier possède un ombre infini de marche alors la longueur de l’hypoténuse mesure 7 unités. |
Cependant, le Théorème de Pythagore nous dit que : 4² + 3² = 16 + 9 = 25
Donc la longueur de l’hypoténuse est de 5 unités et non de 7 !!!!!
Quel est donc l’explication de ce prodige ? 2 unités de différence ce n’est pas rien !! Voici une excellente vidéo de la chaine youtube Maths en tete.
En réalité, la limite de la somme des marches et contremarches n’est pas une droite, et même si on imagine un escalier avec un nombre infini de marches, ces dernières existent toujours et ne peuvent être assimilées à une droite. La notion de limite est toujours à prendre avec des pincettes.
33°/ L’Algorithme de Kaprekar :
Le mathématicien indien D.R. Kaprekar (1905 – 1986) s’est intéressé depuis son enfance aux nombres.
Il a inventé l’algorithme suivant :
Prendre un nombre K (qui ne doit pas être composé des mêmes chiffres) puis réordonner ses chiffres du plus grand au plus petit, puis du plus petit au plus grand. Effectuer la différence du plus grand par le plus petit. Si le nombre de départ contient 3 chiffres on tombe obligatoirement sur 495 de façon cyclique. Si le nombre de départ contient 4 chiffres on tombe obligatoirement sur 6174.
Il existe 3 autres algorithmes : Vous pouvez observer les suites obtenues à l’aide le l’application ci-dessous.
| Algorithme | Méthode | Point fixe | Exemple avec 2543 |
| Algorithme de Kaprekar | Réordonner ses chiffres du plus grand au plus petit, puis du plus petit au plus grand. Effectuer la différence du plus grand par le plus petit. | – Si le nombre de départ contient 3 chiffres : 495
– Si le nombre de départ contient 4 chiffres : 6174 |
5432 – 2345 = 3087 8730 – 0378 = 8352 8532 – 2358 = 6174 7641 – 1467 = 6174 |
| Algorithme dit « retourner » | Écrire les chiffres du nombre K dans l’ordre inverse. Effectuer la différence du plus grand par le plus petit. | zéro | 3452 – 2543 = 909 909 – 909 = 0 0 – 0 = 0 |
| Algorithme dit « alterné » | Pour le premier nombre, inverser le premier et le dernier chiffre. Pour le second, inverser les chiffres du milieu. Effectuer la différence du plus grand par le plus petit. | zéro | 3542 – 2453 = 1089 9081 – 1809 = 7272 7722 – 2277 = 5445 5445 – 5445 = 0 0 – 0 = 0 |
| Algorithme dit « Pair/Impair » | Comme l’algorithme de Kaprekar, à la différence près que les chiffres de rangs pairs sont permutés avec les suivants (s’il a un suivant). | zéro | 5543 – 3455 = 2088 8882 – 2888 = 5994 9995 – 5999 = 3996 9996 – 6999 = 2997 9997 – 7999 = 1998 9998 – 8999 = 999 999 – 999 = 0 0 – 0 = 0 |
34°/ Le paradoxe du duc de Toscane, ou la naissance des probabilités :
Au début du XVIIième siècle, le grand duc de Toscane Cosme II de Médicis (1590-1621) joue avec 3 dés à six faces et s’aperçoit qu’il obtient plus souvent la somme de 10 que celle de 9 lorsqu’il ajoute les trois dés.
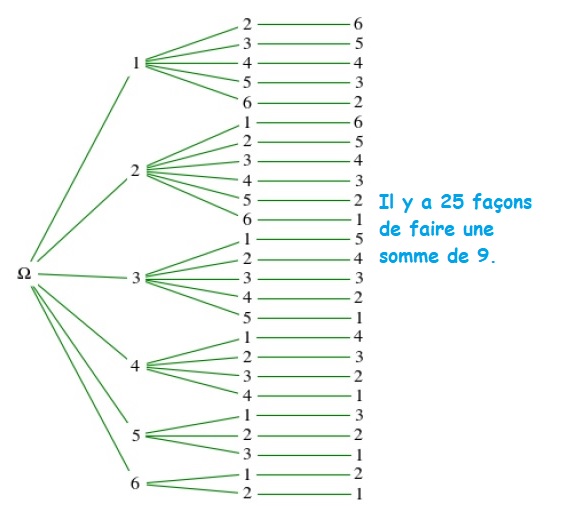
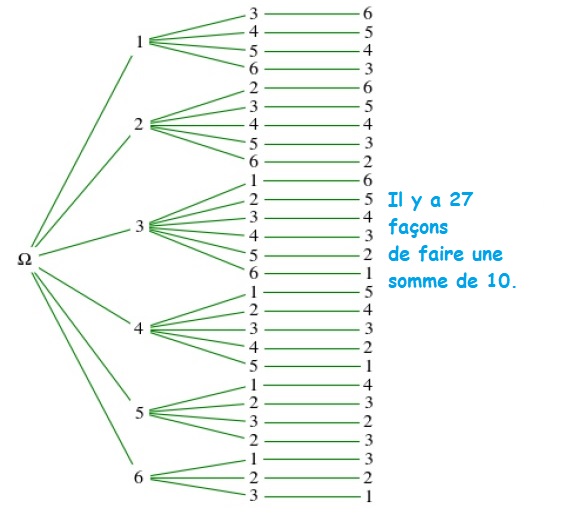
Or, après avoir listé toutes les façons d’obtenir 9 ou 10, il remarque qu’il y en a 6, que ce soit pour 9 ou pour 10. Il y a donc autan de chance de tomber sur les deux valeurs.
Intrigué par la contradiction apparente de ses observations, il va demandé conseil au grand savant de l’époque, Galilée (1564-1642). Un temps perplexe, Galilée fini par découvrir l’explication de ce paradoxe. En effet, si on considère qu’il y a une seule façon d’obtenir la combinaison 1-2-6 par exemple, pour obtenir la somme 9, on se trompe car on oublie que l’ordre a aussi sont importance, et il faut considérer les 6 combinaisons suivantes : 1-2-6; 1-6-2; 2-1-6; 2-6-1; 6-1-2 et 6-2-1.
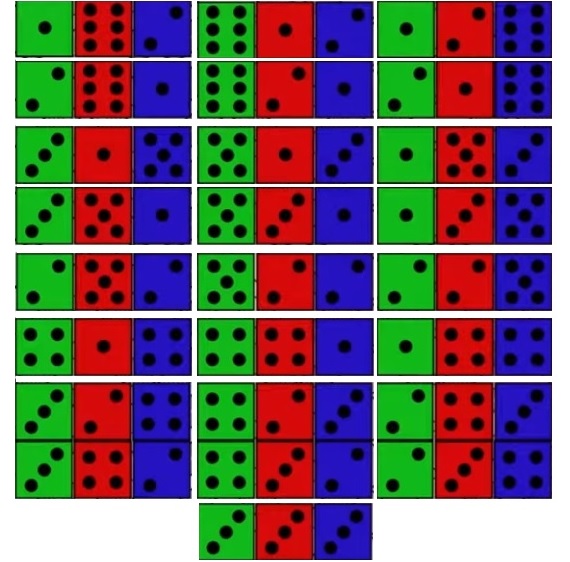
| Somme des 3 dés égale à 9 | Somme des 3 dés égale à 10 |
 |
 |
 |
 |
| il y a 6 x 6 x 6 = 216 combinaisons possibles avec 3 dés :
Donc, la probabilité d’obtenir 9 sera : P(9) = \frac{25}{216}\simeq 0,116 |
il y a 6 x 6 x 6 = 216 combinaisons possibles avec 3 dés :
Donc, la probabilité d’obtenir 10 sera : P(9) = \frac{27}{216}= 0,125 |
La probabilité d’obtenir 10 est donc bien légèrement plus grande que celle d’obtenir 9.
35°/ La conjecture de Poincaré :
La conjecture de Poincaré était une conjecture mathématique du domaine de la topologie algébrique portant sur la caractérisation d’une variété particulière, la sphère de dimension trois ; elle fut démontrée en 2003 par le Russe Grigori Perelman. On peut ainsi également l’appeler théorème de Perelman.
La question fut posée pour la première fois par Henri Poincaré dans son article de 1904, « Cinquième complément à l’analysis situs », et peut s’énoncer aujourd’hui ainsi : Toute 3-variétécompacte sans bord et simplement connexe est-elle homéomorphe à la 3-sphère ?
Elle faisait jusqu’alors partie des problèmes de Smale et des sept « problèmes du prix du millénaire » recensés et mis à prix en 2000 par l’Institut de mathématiques Clay. En 2006, cette démonstration a été validée par l’attribution d’une médaille Fields à Grigori Perelman (qui l’a refusée) ; de plus, en mars 2010, l’institut Clay a officiellement décerné le prix correspondant à Perelman, prix qu’il a également refusé, en raison d’un « désaccord avec les décisions de la communauté mathématique ».
36°/ La loi de Benford :
La loi de Benford, permet de comparer une série de nombre selon le mode additif ou multiplicatif.
Je vous propose le pari suivant : ouvrons le journal, choisissons une page au hasard et notons le premier nombre que nous rencontrons ; si le premier chiffre significatif de ce nombre est supérieur à 3, je vous donnerai 100 €, sinon c’est vous qui me donnerez 100 €.
La proposition vous est , semble-t-il, nettement favorable : il n’y a en effet que trois chiffres qui me font gagner (1, 2, 3), alors qu’il y en a six pour vous ( 4, 5, 6, 7, 8, 9 ) ; le 0 ne compte pas, car il ne peut pas être un premier chiffre significatif. Vous pensez donc gagner environ deux fois sur trois. Serais-je idiot de vous proposer un tel pari ?
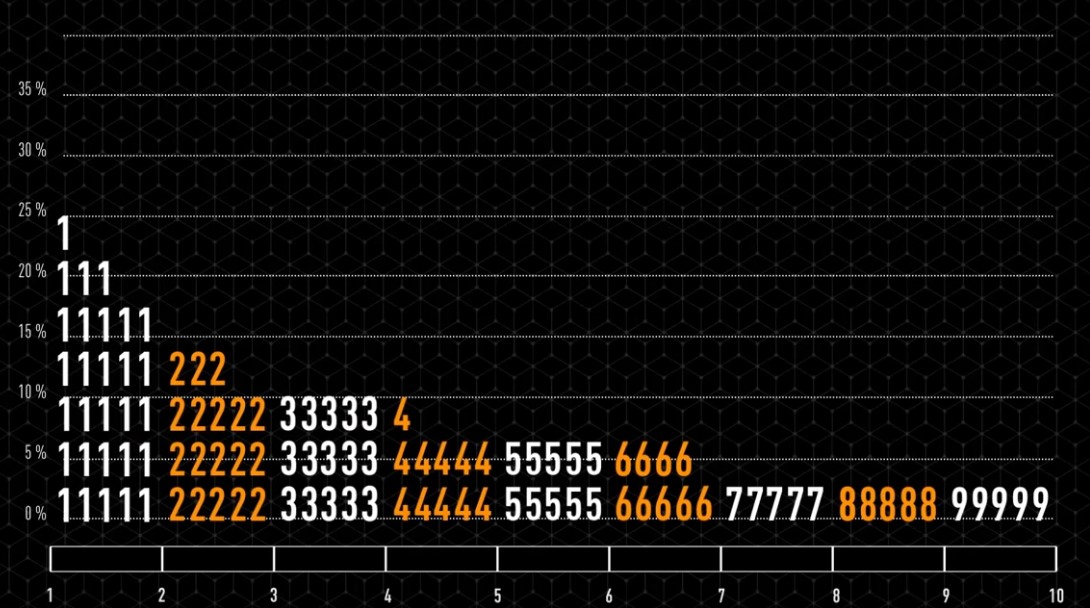
Eh bien non : si vous acceptez, je gagnerai dans plus de 60 pour cent des cas. La loi de Benford indique que, dans un contexte général comme celui d’un article de journal, les probabilités p de rencontrer les différents chiffres comme premier chiffre significatif sont, exprimées en pourcentage :
p(1) = 30,1; p(2) = 17,6 ; p(3) = 12,5 ; p(4) = 9,7; p(5) = 7,9 ; p(6) = 6,7; p(7) = 5,8 ; p(8) = 5,1 ; p(9) = 4,6. Puisque 30,1 + 17,6 + 2,5 = 60,2,
Je gagnerai mon pari dans 60,2% des cas.
Quelle est donc cette loi bizarre du premier chiffre significatif, si contraire à l’intuition ?
Cette loi de Benford n’est pas si compliquée à comprendre.
Si on joue avec un livre de 99 pages, il y a autan de chance de tomber sur chacun des 9 chiffres significatifs : en effet il y a chacun des chiffres de 1 à 9 et 10 chiffres de chaque de 10 à 99. Chaque probabilité est donc de 11/99.
Par contre si le livre possède 299 pages, ce qui est très courant, alors il y aura 11 exemplaires de chaque chiffre de la page 1 à 99 et toutes les autres commenceront par 1 ou 2 pour les pages 100 à 299. P(1) = P(2) = \frac{11+100}{299}=\frac{111}{299} qui est largement supérieur aux autres probabilités qui seront de \frac{11}{299}
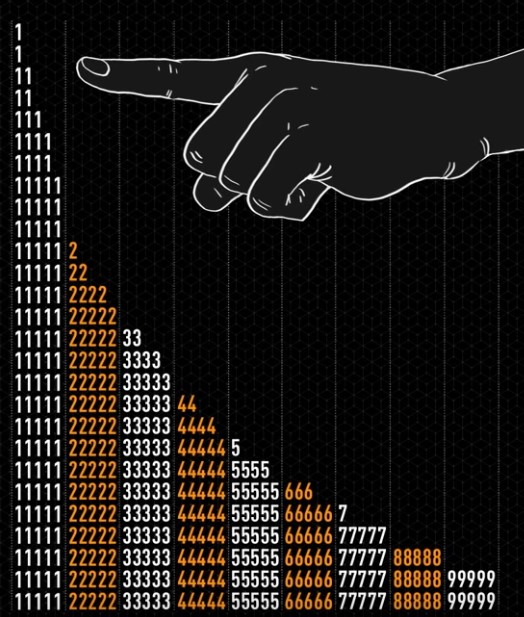
Prenons tous les prix d’un grand supermarché et relevons le premier chiffre de chaque référence. Classons ces chiffres pour déterminer quel est celui qui est le plus présent. Étonnamment les petits chiffres sont plus fréquents que les grands. Il en va de même si on mesure la surface des îles de la Polynésie Française.
 |
Prenons tous les prix d’un grand supermarché et relevons le premier chiffre de chaque référence. |
 |
Classons ces chiffres pour déterminer quel est celui qui est le plus présent. Étonnamment les petits chiffres sont plus fréquents que les grands. |
 |
Il en va de même si on mesure la surface des îles de la Polynésie Française. |
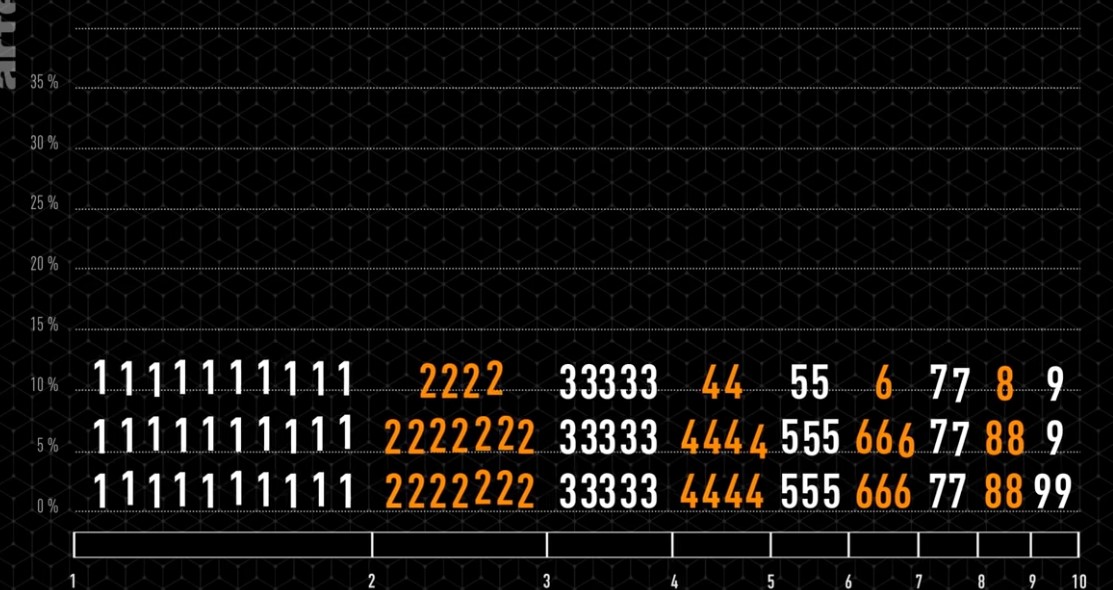
 |
La répartition des chiffres montre une courbe de forme exponentielle. |
 |
En fait c’est l’échelle des abscisses qui n’est pas idéale. Si on utilise une échelle logarithmique, alors la répartition des chiffres devient tout à fait régulière. On utilise cette loi de Benford pour savoir si une suite de nombre a été créer aléatoirement par un ordinateur ou si elle est naturelle. Par exemple les données comptables d’une entreprise ont toutes les chances d’avoir été bidouillées si la répartition des premiers chiffres est trop régulière. |
Je vous propose différents exercices, tous aussi contre-intuitifs les uns que les autres :
a°/ La distance terre-lune :
b°/ La fourmi, le chimpanzé et le Gorille :
c°/ La balle de ping-pong, la terre et le soleil :
d°/ Mille million milliard :
Notre erreur provient sans nul doute de la façon dont nous avons appris à compter. Jusqu’à cent, nous comptons de 10 en 10 : dix, vingt, trente …, mais ensuite c’est plutôt de 1000 en 1000 : mille, million, milliard ….
37°/ Des sommes de réel étonnantes :
En fait toutes les opérations qui vont suivre, sont fausses dans l’ensemble des nombres réels mais exactes dans l’ensemble des nombres p-adiques.
Les nombres p-adiques forment une extension particulière du corps \mathbb{Q} des nombres rationnels, découverte par Kurt Hensel en 1897. Ce sont des nombres composés d’une suite de chiffre infinie à gauche de la virgule, mais toujours finie à droite de la virgule.
Par exemple : ….9999 signifie que ce nombre est composé d’une infinité de 9.
Dans cet ensemble les opérations de bases donnent des résultats particuliers.
1°/ L’incroyable addition : 1 + 2 + 3 + 4 + … = -1/12
La somme de tous les entiers ne donne pas l’infini mais -1/12 !!!!
Le grand mathématicien indien Srinivasa Ramanujan est à l’origine de cette étrange égalité.
En voici la démonstration :
Posons : C = 1 + 2 + 3 + 4 + 5 + 6 + …
Donc : 4C = 4 + 8 + 12 + 16 ….
Effectuons la soustraction suivante : S = C – 4C = -3C
Posons cette soustraction en décalant 4C pour plus de commodité :
C = 1 + 2 + 3 + 4 + 5 + 6 + …
– 4C = 4 + 8 + 12 + …
-3C = 1 – 2 + 3 – 4 + 5 – 6 + …. = S
Calculons 4S :
S = 1 – 2 + 3 – 4 + 5 – 6 + …
+ S = 1 – 2 + 3 – 4 + 5 – 6 + …
+ S = 1 – 2 + 3 – 4 + 5 – 6 + …
+ S = 1 – 2 + 3 – 4 + 5 – 6 + …
4S = 1 + 0 + 0 + 0 + 0 + 0 + 0 + …. = 1
Donc : S = -3C = 1/4 Donc : C = -1/12
2°/ Une autre addition étonnante : 0 = -1
Posons : C = 1 + 2 + 3 + 4 + 5 + 6 + …
2C = 2 + 4 + 6 + 8 + 10 + 12 + …
Donc :
2C = 2 + 4 + 6 + 8 + 10 + 12 + …
– C = 1 + 2 + 3 + 4 + 5 + …
C = 2 + 3 + 4 + 5 + 6 + 7 + … = C – 1
Donc : C = C – 1 et C – C = -1 donc : 0 = -1
3°/ Une autre addition étonnante : Voici une somme infinie qui ne donne pas l’infinie mais -1 !!!
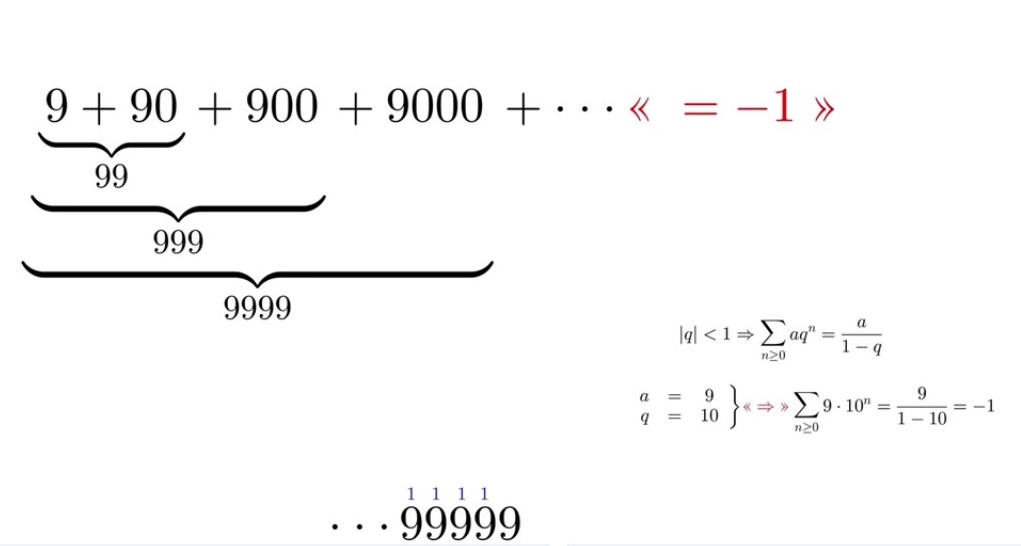
4°/ Voici deux autres additions : celle de gauche est correcte mais pas celle de droite.

Certains d’entre vous seront peut-être intrigués par le résultat paradoxal des opérations de la fig. 2, en fait : infini ≠ -2.
D’ailleurs, on peut trouver dans n’importe quel manuel de mathématiques que la somme des puissances de 2 donne :
2 n + 2 n -1 + 2 n -2 + … + 2 3 + 2 2 + 2 1 = 2 n +1 – 2 = 2(2 n – 1)
Alors, où est l’erreur ?
Les mathématiques derrière le fait : l’indétermination de ∞ – ∞
Alors que la limite de la somme des fractions peut converger vers une limite, dans ce cas précis vers 1, la somme des puissances n’a pas de limite car elle ne peut exister puisque : \lim_{n\to\infty}S_{n}=\infty
Ainsi, vous ne pouvez pas soustraire S des deux côtés de l’équation ; car cela reviendrait à écrire : – 2 + ∞ – ∞ = 2∞ – ∞
et le problème est que même dans les réels étendus * , ∞-∞ est indéterminé. Cela n’équivaut à rien, et certainement pas à zéro. Bref, on ne peut pas simplement annuler les infinis.
* En mathématiques, le système de nombres réels affinement étendu est obtenu à partir du système de nombres réels R en ajoutant deux éléments : +∞ et -∞ (lus respectivement comme l’infini positif et l’infini négatif). Ces nouveaux éléments ne sont pas de vrais chiffres. Il est utile pour décrire divers comportements limites en calcul et en analyse mathématique, en particulier dans la théorie de la mesure et de l’intégration.
38°/ Les 7 problèmes du millénaire :
Le 24 mai 2000, le Clay Mathematics Institute (CMI) présente au Collège de France sept problèmes majeurs des mathématiques. Chacun est doté d’un prix d’un million de dollars pour celui qui en arriverait à bout.
Malheureusement ces problèmes ne sont pas à la portée du profane et sont plutôt un défi à la communauté scientifique dans le but de faire progresser les recherches en mathématiques, en informatique et en physique.
1°/ La conjecture de Birch et Swinnerton-Dyer : Quand les solutions d’une équation algébrique sont situées sur une variété abélienne, la taille du groupe des solutions rationnels est reliée au comportement de la fonction Zeta ?(s) associée au voisinage de s=1. Si ?(1)=0 alors il y a une infinité de solutions rationnelles et réciproquement, si ?(1)?0, il y a seulement un nombre fini de solutions rationnelles.
2°/ La conjecture de Hodge : Pour une certaine classe d’espace, les variétés algébriques projectives, appelées cycles de Hodge sont des combinaisons linéaires rationnelles d’objets ayant une réelle nature algébrique (les cycles algébriques).
3°/ Les équations de Navier-Stokes : Le défi consiste à faire progresser les théories mathématiques liées aux équations de Navier-Stockes dans le but d’expliquer des phénomènes tel le mouvement des vagues produites par un bateau en déplacement.
4°/ Le P problème et le NP problème : On appelle P problème tout problème qui consiste à trouver une liste d’éléments dans un ensemble donné et ce relativement à un critère fixé à l’avance. Le NP problème est opposé au P problème : il consiste à vérifier si une liste donnée est en adéquation avec les conditions données au préalable.
5°/ La conjecture de Poincaré : Soit une variété compacte V simplement connexe, à 3 dimensions, sans bord. Alors V est homéomorphe à une hypersphère de dimension 3.
En 2006, le russe Gregori Perelman se voit décerner la médaille Fields pour avoir démontré la conjecture de Poincaré. Mais le mathématicien russe la refuse ainsi que la récompense de un million de dollars promise par la Clay Mathematics Instituts. La seule raison invoquée est qu’il se sentait isolé de la communauté mathématique internationale.
6°/ L’hypothèse de Riemann : Les solutions de l’équation ?(s)=0 se situent le long d’une ligne droite verticale, où ? est la fonction Zeta de Riemann.
7°/ La théorie de Yang-Mills : La théorie de Yang et Mills est construite sur un modèle géométrique expérimental qui décrit l’interaction forte des particules élémentaires. Elle n’est par contre pas comprise d’un point de vue théorique. Elle fait intervenir une propriété appartenant au monde de la mécanique quantique : certaines particules quantiques ont une masse positive alors que l’onde associée voyage à la vitesse de la lumière.
39°/ Le paradoxe de Bertrand :
Les probabilités sont étonnantes. Prenons un triangle équilatéral et son cercle circonscrit. Quelle est la probabilité pour qu’une corde, choisie au hasard,
soit plus longue que le côté du triangle équilatéral inscrit ?
Et bien suivant comment on fabrique ces cordes, la probabilité sera ne sera pas la même !!
Cas 1 : Corde définie par un sommet du triangle et un point du cercle. Probabilité = 1/3
Cas 2 : Un point dans le cercle inscrit au triangle. Probabilité = 1/4
Cas 3 : Point sur un rayon perpendiculaire à un côté du triangle. Probabilité = 1/2
Dans chacun des cas on a bien fabriquer toutes les cordes possibles, mais on ne peut calculer une probabilité correctement que si les consignes de départs sont claires, et ce n’est pas le cas ici !!
Une petite variante très paradoxale : prenons un cube de côté c. On vous demande de parier sur deux propositions:
– Proposition n°1 : le côté c étant compris entre 1 et 10, vous pariez que c est compris entre 1 et 7 ou entre 7 et 10 ?
– Proposition n°2 : le volume c3 étant compris entre 1 et 1 000, vous pariez que le volume est compris entre 1 et 343 ou entre 343 et 1 000 ?
| Proposition n°1 | Proposition n°2 |
|
entre 1 et 7 il y a 7 possibilités : probabilités supérieures, c’est mon choix. entre 7 et 10 il y a 4 possibilités. |
entre 1 et 343 il y a 343 possibilités. entre 343 et 1 000 il y a 658 possibilités : probabilités supérieures, c’est mon choix. |
Le choix a l’air simple et basique, sauf que ces 2 propositions sont en fait parfaitement identiques mais les réponses diamétralement opposées.
En effet, pour un cube dont le côté varie de 1u à 7u, son volume varie de 13 = 1 u3 à 73 = 343 u3.
Pour un cube dont le côté varie de 7u à 10u, son volume varie de 73 = 343 u3 à 103 = 1 000 u3.
Donc notre intuition nous joue un drôle de tour ainsi que le facteur d’agrandissement des volumes.
40°/ La trompette de Gabriel :
Cette figure a été étudiée par le physicien italien Evangelista Torricelli au XVIIe siècle.
 |
 |
| En partant de la fonction \frac{1}{x} et en la faisant tourner autour de l’axe des abscisses. Calculons le volume et la surface entre x = 1 et x = a où a > 1. | On obtient un volume infini appelé trompette de Gabriel. |
Calcul du volume : V = \pi \int_{1}^{a} \frac{1}{x^{2}}dx = \pi (1-\frac{1}{a})
Le volume de la trompette est donc la limite de V quand a tend vers l’infini : \displaystyle \lim_{ a \to \infty }\pi (1-\frac{1}{a}) = \pi qui est un nombre rationnel mais qui n’est pas infini.
Calcul de la surface : A = 2\pi \int_{1}^{a}\frac{\sqrt{1+\frac{1}{x^{2}}}}{x^{2}}dx > 2\pi \int_{1}^{a}\frac{\sqrt{1}}{x}dx = 2\pi \ ln\ a
La surface de la trompette est donc la limite de A quand a tend vers l’infini : \displaystyle \lim_{ a\to \infty } 2\pi \ ln\ a = \infty
Donc la trompette de Gabriel possède une surface infinie mais un volume fini !!!
Si on voulait peindre cette trompette il nous faudrait donc un pot de peinture infini, mais il suffirait de remplir l’intérieur de la trompette, il là le pot de peinture serait fini.
41°/ Le paradoxe de Simpson : étude sur les placébos
Voici une étude sur l’efficacité d’un placébo, qui est un médicament sans principe actif.
On a donné soit un médicament soit un placébo à 80 hommes et 80 femmes. On a calculer le taux de personnes guéries.
|
|
||||||||||||||||||||||||
|
Il faut donner le placébo aux hommes et aux femmes, mais le médicaments si on ne connait pas leur sexe !!!!! Il y a 2 critères à prendre en compte : la prise de médicament/placébo et le genre des personnes. Il s’agit d’évaluer des facteurs croisés qui perturbent la proportionnalité. |
42°/ Tous les triangles sont équilatéraux :
1°/ Prenons un triangle quelconque ABC et traçons la médiatrice de [BC] et la bissectrice de l’angle \widehat{A}. Appelons E leur point d’intersection.
2°/ Traçons les perpendiculaires à (AB) et (AC) passant par E. Elles coupent (AB) en F et (AC) en G.
3°/ Les triangles AEF et AGE ont un angle droit, les angles \widehat{FAE} et \widehat{EAG} sont égaux et l’hypoténuse [AE] en commun. Ils sont donc égaux et AF = AG.
4°/ Les triangles BED et DEC ont un angle droit, un côté [ED] en commun et BD = DC car D est le milieu de [BC]. Ils sont donc égaux et EB = EC.
5°/ Les triangles BEF et CGE ont un angle droit, EB = EC et EF = EG. Ils sont donc égaux et FB = GC.
6°/ \left.\begin{matrix}AF=AG\\BF=GC\end{matrix}\right\}\Rightarrow AB=AC. Donc ABC est isocèle en A.
7°/ On peut refaire la même démonstration en B et en C.
Le triangle est donc équilatéral !!!!!
Solution : En fait, le schéma est un peu faux !!!
La bissectrice ne coupe pas parfaitement l’angle \widehat{A} en deux parties égales et le point E devrait être à l’extérieur du triangle.
Le raisonnement est en tout point exact, et les triangles AEF et AGE sont bien identiques, ainsi que BED et DEC et ainsi que BEF et CGE.
Cependant, si en effet si AF = AG et BF = GC, AB = AF + BF alors que AC = AG – CG
43°/ Les limites de bon sens :
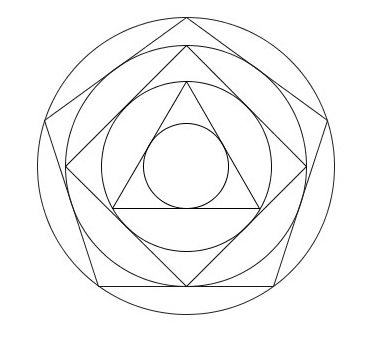
Construisons les figures suivantes :
|
|
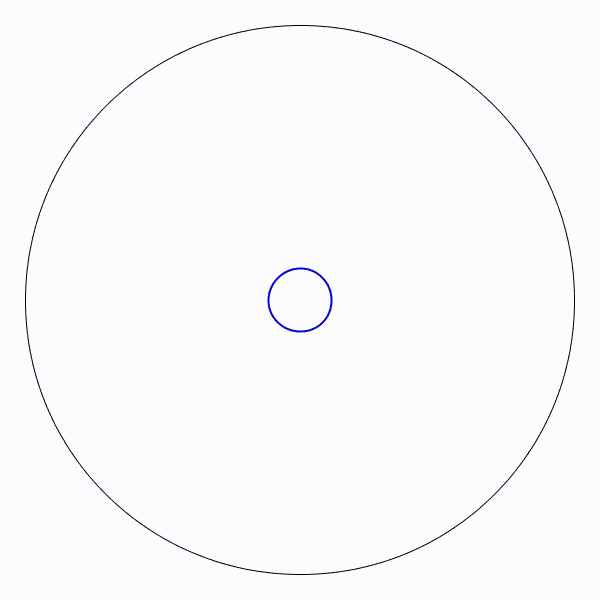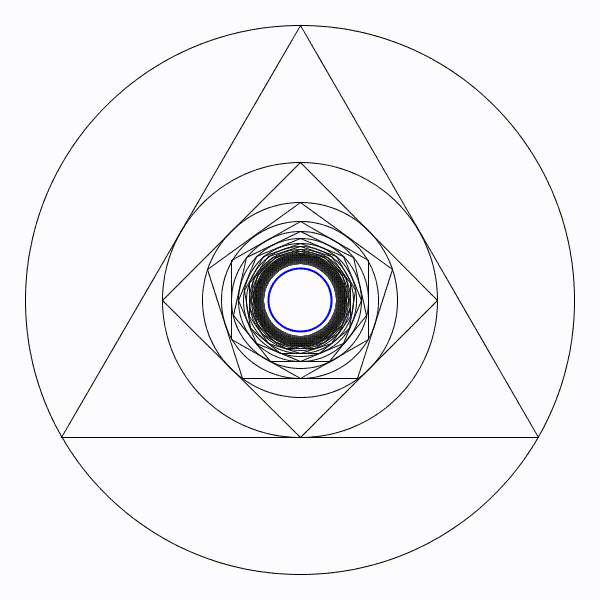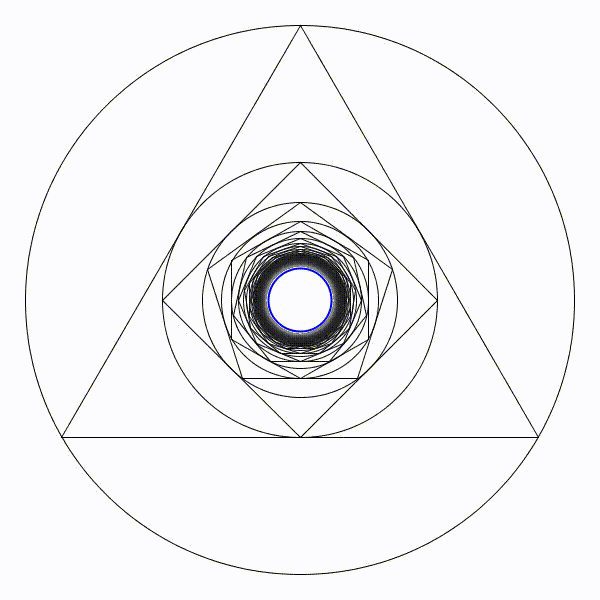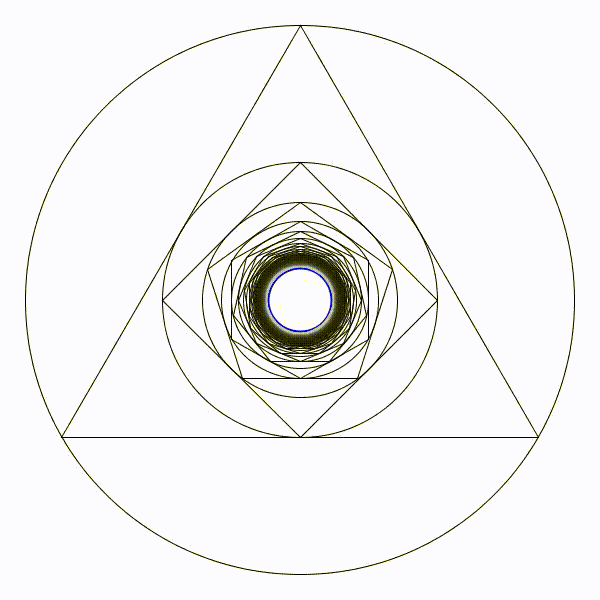
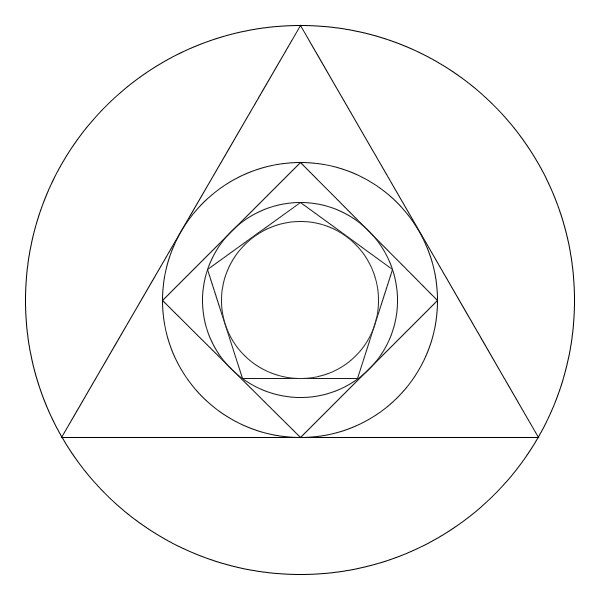 Partons d’un cercle de rayon une unité, puis construisons son triangle équilatéral inscrit à l’intérieur. Puis un nouveau cercle inscrit et son carré inscrit. Et ainsi se suite en alternant un cercle et un polygone dont le nombre de coté augmente de un à chaque étape. Partons d’un cercle de rayon une unité, puis construisons son triangle équilatéral inscrit à l’intérieur. Puis un nouveau cercle inscrit et son carré inscrit. Et ainsi se suite en alternant un cercle et un polygone dont le nombre de coté augmente de un à chaque étape. |
|
|
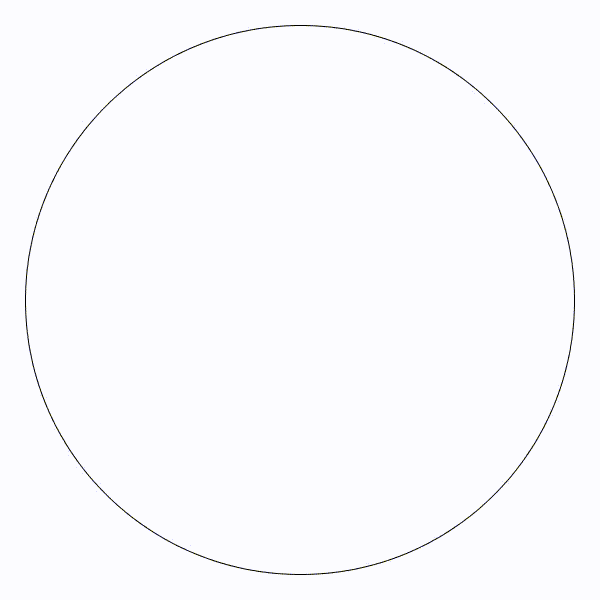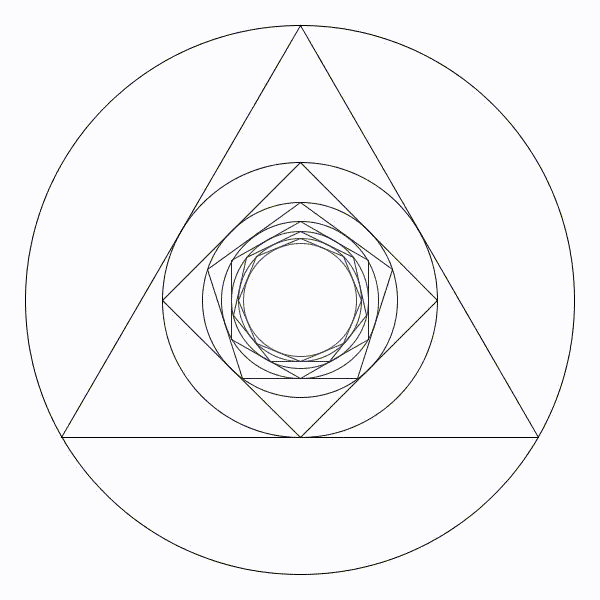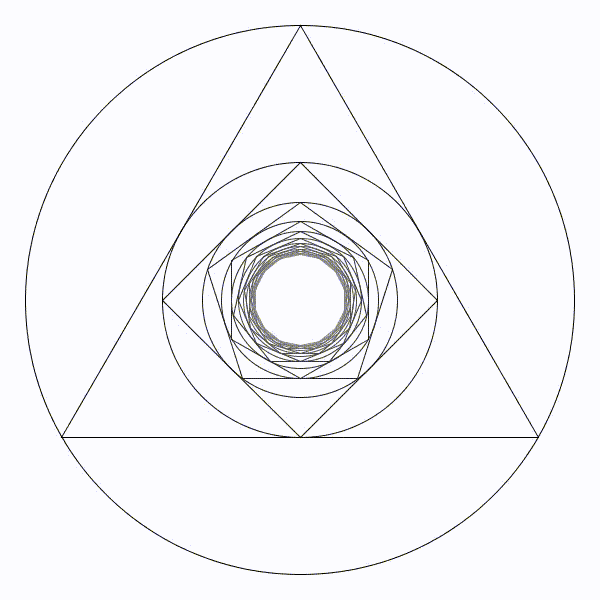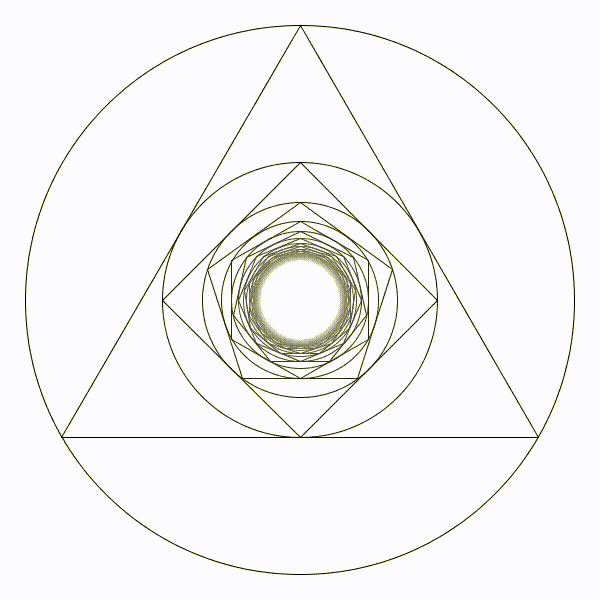 Il parait évident que le rayon des cercles va tendre vers zéro. Il parait évident que le rayon des cercles va tendre vers zéro. |
Et bien ce n’est pas si simple. Voir les explications détaillées ici :
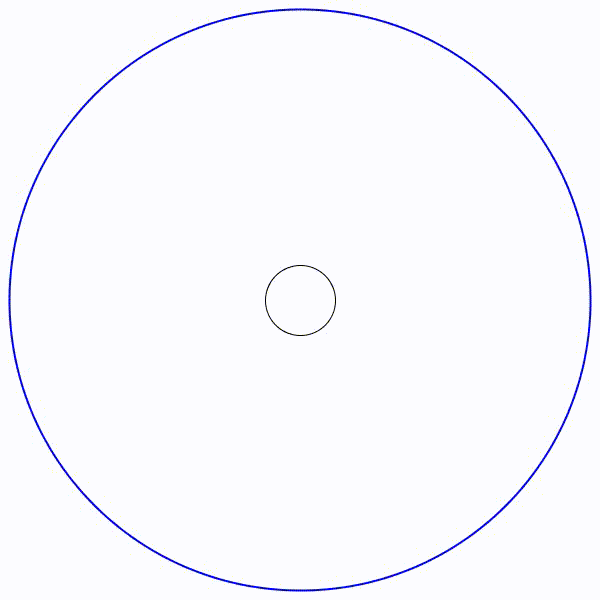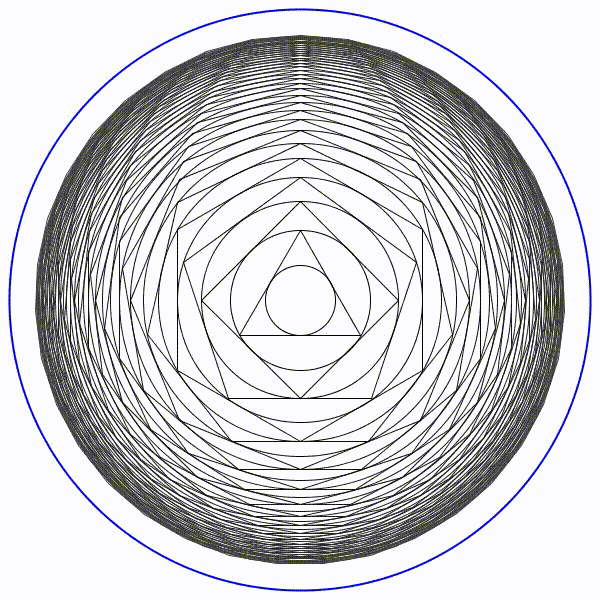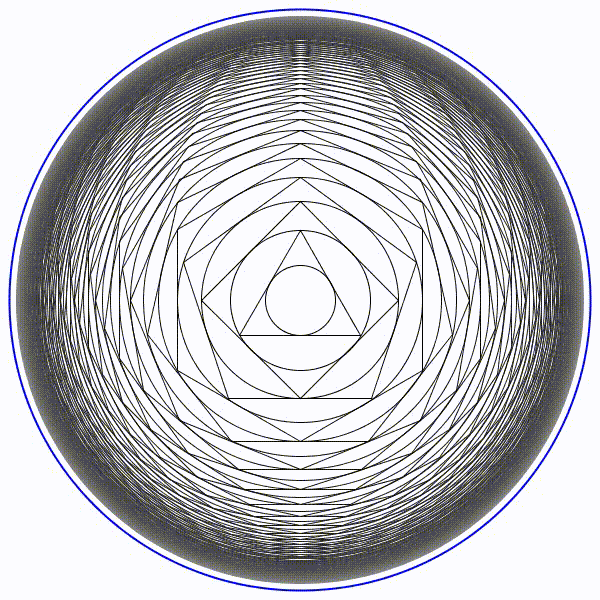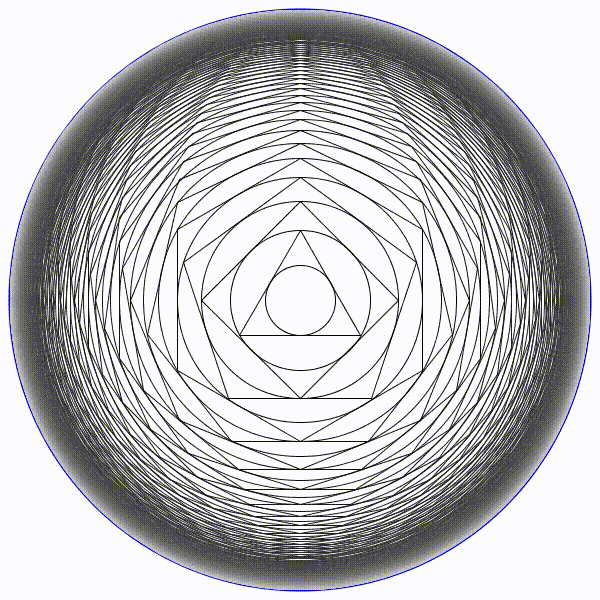 Le cercle limite de rayon en bleu sera de presque 8,7 unités. Le cercle limite de rayon en bleu sera de presque 8,7 unités. |
 Le cercle limite de rayon en bleu sera de presque 0,115 unités. Le cercle limite de rayon en bleu sera de presque 0,115 unités. |
44°/ Je suis le Pape :
Un étudiant de philosophie demande au logicien Bertrand Russell :
« Prétendez-vous que, de l’assertion 2 + 2 = 5, il s’ensuit que vous êtes le pape ?
— Oui, bien sûr, dit Russell.
— Pouvez-vous le prouver ? demanda l’étudiant sceptique.
— Certainement, répliqua Russell en poursuivant.
Supposons donc que 2 + 2 = 5.
Soustrayons 2 de chaque membre de l’égalité, nous obtenons 2 = 3 et par symétrie 3 = 2.
Soustrayons 1 de chaque côté, il vient 2 = 1.
Le pape et moi sommes 2 personnes, et puisque on part du principe que 2 + 2 = 5 et que donc 2 = 1, deux personnes équivalent à une seule. Le pape et moi sommes donc une seule et même personne. Par suite, je suis le pape ! »
45°/ Le paradoxe de la roue d’Aristote :
Voici une roue sur laquelle on a tracé 2 cercles concentriques de rayon différents. En faisant tourner cette roue, on se rend compte que les 2 points repérer sur les 2 cercles parcourent la même distance alors que les circonférences sont différentes. Comment cela est-il possible ?
L’explication de ce paradoxe vient du fait que les trajectoires des 2 points ne sont pas des cercles :
 |
La trajectoire bleue extérieure est 2 demis cercles, ce qui fera bien un cercle entier de longueur 2πR. La trajectoire rouge intérieure est plus complexe et elle est égale à la trajectoire bleue. |

 Partons d’un cercle de rayon une unité, puis construisons son triangle équilatéral circonscrit. Puis un nouveau cercle circonscrit et son carré circonscrit. Et ainsi se suite en alternant un cercle et un polygone dont le nombre de coté augmente de un à chaque étape.
Partons d’un cercle de rayon une unité, puis construisons son triangle équilatéral circonscrit. Puis un nouveau cercle circonscrit et son carré circonscrit. Et ainsi se suite en alternant un cercle et un polygone dont le nombre de coté augmente de un à chaque étape. Il parait évident que la figure va augmenter indéfiniment.
Il parait évident que la figure va augmenter indéfiniment.