Il vous est certainement déjà arrivé de vivre l’expérience suivante. Vous êtes confortablement installé dans un train en attendant le départ. En regardant par la fenêtre, vous voyez le train stationné à côté avancer. Mais une fois que les trains se séparent, vous vous rendez compte que c’est le vôtre qui avançait et non celui d’à côté !! D’ailleurs aucuns des passagers de chaque train ne peut véritablement savoir qui se déplace, car si on regarde vers l’intérieur de notre compartiment, rien ne bouge. Tout ce qui est dans le compartiment est fixe, on en conclue que l’on ne se déplace pas.
En physique on parle de référentiel pour désigner le lieu de départ d’un mouvement. Pour chaque passager, le référentiel c’est sa propre place et donc ce sera toujours l’autre train que se déplacera.
Dans le cas des trains, les distances sont absolues c’est-à-dire qu’elle ne dépendent pas du référentiel choisit. Que je choisisse un train ou un autre, les distances parcourues seront les mêmes dans des directions opposées.
Mais notre cher Einstein a démontré que le temps était relatif, c’est-à-dire dépendant d’un référentiel . Si les 2 trains se déplacent à une vitesse proche de la lumière, des événements vraiment particuliers se produisent.
1°/ Une vidéo :
2°/ Les explications de la vidéo :
3°/ Une calculatrice : pour tester différentes configurations
4°/ Démonstration de la formule :
5°/ L’expérience grandeur nature :
1°/ Une vidéo :
2°/ Les explications de la vidéo :
C’est le paradoxe des jumeaux de Langevin présenté par Paul Langevin au congrès de Bologne en 1911 : pendant qu’un des jumeaux reste sur terre, l’autre monte dans une fusée et fait l’aller-retour vers Proxima du centaure par exemple, qui est situé à quatre années-lumière, notée AL. Si la vitesse de la fusée représente les deux tiers de la vitesse de la lumière (vitesse inaccessible pour le moment), alors le voyage dans le référentiel terre sera de 12 ans alors qu’il sera de 9 ans pour le référentiel fusée. Le jumeau de la fusée sera 3 ans plus jeune que son frère !!! Bon il faut passer pas mal de temps dans une fusée tout de même.
A noter que si la vitesse de la fusée était de 99 % de la vitesse de la lumière, le voyage aurait duré 8 ans sur terre et seulement 1 an dans la fusée.
 |
Graphique du temps de parcourt en fonction de la distance en année-lumière. La courbe ainsi fabriquée s’appelle la ligne d’univers.
Courbe rouge : à la vitesse de la lumière, une année-lumière est parcourue en une année. C’est la ligne d’univers maximum. Courbe verte : ligne d’univers du jumeau resté sur terre, qui ne se déplace pas puisque on choisit le référentiel terrestre. Courbe bleue : ligne d’univers du jumeau de la fusée. La première partie dure 4,5 ans pour lui mais 6 ans pour son frère, car ils ne sont pas dans le même référentiel et que le temps est relatif. Arrivée à Proxima du centaure, il revient sur terre, en mettant de nouveau 4,5 ans pour lui et 6 ans pour son frère. Bilan de l’aller-retour : 12 ans pour le jumeau resté sur terre et 9 ans pour celui de la fusée. |
On peut effectuer le calcul :
| c : vitesse de la lumière = 300 000 km/s | Rv : Rapport des vitesses = V/c (si par exemple Rv = 0,8 cela veut dire que la fusée va à 0,8c cad aux 4/5ième de la vitesse la lumière). |
| V : Vitesse de la fusée | Rd : Rapport des durées = T/t ( ici Rd = 1,342 cela veut dire que le temps passe 1,342 fois plus vite sur terre que dans la fusée). |
| T : Temps relatif sur terre en années | t : temps dans la fusée |
On a la formule suivante qui lie Rd et Rv :
| Rv = V/c | Temps relatif sur terre en années | Temps dans la fusée | ||||
| V | en fraction | en % | Rd | T | t = T/Rd | T – t |
| 0,5c | 1/2 | 50 | 1,155 | 25 | 21,65 ans | 3,35 ans |
| 0,66666666c = 2/3 de c | 2/3 | 66,666666 | 1,342 | 6 | 4,47 ans | 1,53 ans |
| 0,8c | 4/5 | 80 | 1,667 | 6 | 3,6 ans | 2,4 ans |
| 0,86c | 6/7 | 86 | 1,960 | 6 | 3,06 ans | 2,94 ans |
| 0,995c | 1 | 99,5 | 10,013 | 6 | 218,87 J | 5 ans 146 J |
| 0,997c | 1 | 99,7 | 12,920 | 6 | 169,62 J | 5 ans 195 J |
| 0,999c | 1 | 99,9 | 22,366 | 6 | 97,98 J | 5 ans 268 J |
| 0,9999c | 1 | 99,99 | 70,712 | 6 | 30,99 J | 5 ans 334 J |
| 0,99999999c | 1 | 99,999999 | 7071,068 | 6 | 7,44 h | 5 ans 364,9 J |
| 0,999999999c | 1 | 99,9999999 | 22360,680 | 6 | 2,35 h | 5 ans 365,15 J |
Plus on s’approche de la vitesse de la lumière et plus la différence entre les temps est considérable.
Par exemple à 0,999 999 999 fois la vitesse de la lumière, 1 seconde dans la fusée représente 6,22 jours sur terre !!
A 66,66% ou les 2/3 de la vitesse de la lumière 4,5 ans dans la fusée représentent 6 ans sur terre.
| V | en fraction | en % | Rd | T terre = t x Rd | t fusée en seconde |
| 0,5c | 1/2 | 50 | 1,155 | 1,16 s | 1 |
| 0,66666666c | 2/3 | 66,666666 | 1,342 | 1,35 s | 1 |
| 0,8c | 4/5 | 80 | 1,667 | 1,67 s | 1 |
| 0,86c | 6/7 | 86 | 1,960 | 1,96 s | 1 |
| 0,995c | 1 | 99,5 | 10,013 | 10,02 s | 1 |
| 0,997c | 1 | 99,7 | 12,920 | 12,92 s | 1 |
| 0,999c | 1 | 99,9 | 22,366 | 22,37 s | 1 |
| 0,9999c | 1 | 99,99 | 70,712 | 1,18 min | 1 |
| 0,99999999c | 1 | 99,999999 | 7071,068 | 1,97 J | 1 |
| 0,999999999c | 1 | 99,9999999 | 22360,680 | 6,22 J | 1 |
3°/ Une calculatrice : pour tester différentes configurations
Quelques exemples :
| Véhicule | temps propre |
Vitesse en km/h | Différence T-t |
| Concorde | 0,5 h | 2 000 km/h | 3,1 nanoseconde |
| ISS (Station Spatiale Internationale) | 1,32 h (le tour de la terre) | 28 000 km/h | 1,6 millionième de secondes |
| Train à la moitié de la vitesse lumière | 21,65 ans | 540 000 000 km/h ( C/2 ) | 3,35 ans |
4°/ Démonstration de la formule :
Intéressons-nous à la durée de parcours d’un éclair lumineux envoyé sur un miroir et revenant à son point de départ.
Nous admettrons, comme principe de base, que la lumière se déplace dans le vide à la vitesse de 300 000 km/sec. Cette vitesse notée C, est une constante de l’univers, établit grâce à la théorie de la relativité.
Quelle sera la durée de l’aller-retour ?
Si le miroir et l’observateur sont immobiles l’un par rapport à l’autre, les deux événements, émission et retour de l’éclair, ont lieu au même endroit, et sont repérés par une même horloge. La durée t du temps écoulé entre les deux événements est :
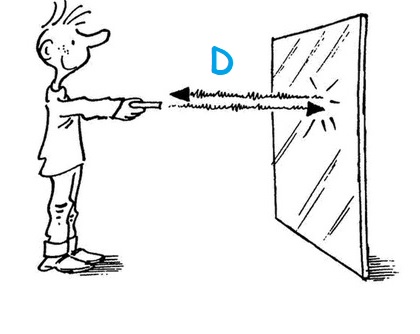 |
D = Distance miroir-observateur
t = temps mis par la lumière pour faire l’aller-retour d’où : |
Si en revanche, l’observateur se déplace avec une vitesse v par rapport à l’espace dans lequel se situe le miroir et l’horloge qui sont immobiles, le trajet suivi par la lumière tiendra compte de ce déplacement. Notons 2D’ sa longueur. La durée du parcours sera donc T :
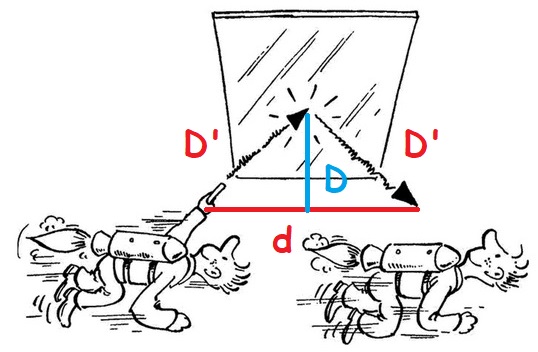 |
D = Distance miroir-observateur fixe initial D’ = Distance miroir-observateur en mouvement d = distance parcourue par l’observateur entre l’envoi de la lumière et sa réception T = temps mis par la lumière entre l’envoi de la lumière et sa réception v = vitesse de déplacement de l’observateur |
On sait que :
Donc le temps T mis par la lumière entre l’envoi de la lumière et sa réception est égal à :
Remarque : Quand v est très petit devant C, tend vers 0, et T = t
Cette formule est célèbre, mais l’important est d’en comprendre la signification.
Un même événement a une durée différente selon que celui qui la mesure est au repos ou en mouvement par rapport à lui.
Dans le premier cas, la durée correspond à ce que l’on appelle le temps propre t, dans le second un temps impropre T qui sera toujours plus grand.
Par exemple, si je vais de Lille à Marseille en avion, les horloges des deux aéroports sont en mouvement par rapport à l’avion, elles mesurent le temps impropre, alors que ma montre est fixe dans le référentiel qu’est l’avion, elle mesurera donc le temps propre. La différence est pourtant bien faible.
Même avec le concorde volant à 2000 km/h sur les 1000 km de parcours, on obtient t = 30 min et T = 30,000 000 000 06 min. On comprendra qu’une telle différence est insignifiante et invisible dans la vie courante. Cependant, pour des objets se déplaçant à des vitesses proches de la lumière, comme des objets célestes, seule la conception du temps proposé par Einstein permet de rendre compte de la réalité.
5°/ L’expérience grandeur nature :
Bien entendu tous ceci est théorique et il serait difficile de le prouver par une expérience car il s’agirait d’aller au moins à la moitié de la vitesse de la lumière.
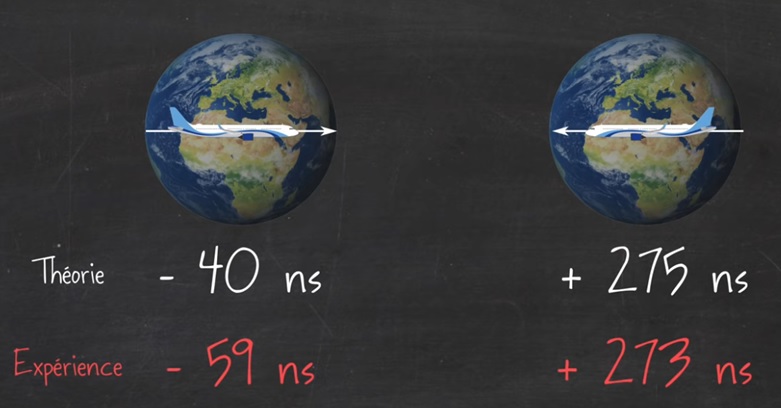
| Cependant en 1971, deux physiciens Américains, Hafele et Keating effectuent l’expérience suivante. Ils projettent de faire le tour du monde dans le sens inverse de la rotation de la terre, vers l’ouest donc, en emportant 4 horloges atomiques capables de mesurer un dixième de nanoseconde. Leurs calculs théoriques prévoyaient un décalage de 275 nanosecondes par rapport aux même horloges atomiques restées sur terre. Ils obtinrent 273 nanosecondes. Pour être très rigoureux, ils firent la même expérience dans le sens de la rotation terrestre. Ils prévoyaient un retard de 40 nanosecondes, ils obtinrent – 59 nanosecondes.
De plus, la gravité joue aussi un rôle dans la déformation de l’espace-temps. Ainsi le temps s’écoule moins vite à proximité d’une masse importante comme un trou noir. On peut observer ce phénomène sur terre : une horloge atomique placée à 2056 m d’altitude (éloignée du centre de gravité terrestre donc le temps passe plus vite) pendant 24 heures aura 20,485 nano seconde d’avance par rapport à une horloge atomique restée à 0 m. En 2010 des physiciens ont même été capable de mesurer une différence de temps entre deux horloges séparées par 33 cm d’altitude. |
 |