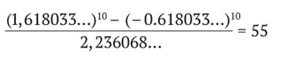A°/ Nombres particuliers :
B°/ Un peu de calcul mental : Utilisons 4 fois le même chiffre
C°/ 666 un nombre maléfique et le nombre de Belphégor :
D°/ Somme des n premiers nombres entiers impairs = n² :
E°/ Somme des n premiers carrés = n (n+1) (2n+1) / 6 :
F°/ Le cube de la somme de deux nombres : (a+b)³
G°/ Théorème de Nicomaque : Somme des n premiers cubes = (1 + 2 + 3 + 4 + 5 + 6 + 7 + … + n )²
H°/ Les nombres Phénix :
I°/ Les nombres remarquables :
J°/ La fonction 91 :
K°/ Les équations palindromiques :
L°/ Une jolie démonstration :
M°/ Le nombre d’or :
N°/ La somme d’une suite géométrique infinie est finie :
O°/ Le nombre un : Pourquoi faire simple quand on peu faire compliqué.
P°/ Le nombre e :
Comme amuse-gueule, voici une vidéo très originale qui nous présente toutes sorte de nombre et de concept mathématique : pour avoir des explications Animation vs. Math
A°/ Nombres particuliers :
Vous pensez bien connaître les mathématiques…
Alors, le saviez-vous :
|
0×9 + 8 = 8 9×9 + 7 = 88 98×9 + 6 = 888 987×9 + 5 = 8888 9876×9 + 4 = 88888 98765×9 + 3 = 888888 987654×9 + 2 = 8888888 9876543×9 + 1 = 88888888 98765432×9 + 0 = 888888888 987654321×9 – 1 = 8888888888 |
1×9 + 2 = 11 12×9 + 3 = 111 123×9 + 4 = 1111 1234×9 + 5 = 11111 12345×9 + 6 = 111111 123456×9 + 7 = 1111111 1234567×9 + 8 = 11111111 12345678×9 + 9 = 111111111 123456789×9 + 10 = 1111111111 |
13 + 53 + 33 = 153 33 + 73 + 03 = 370 33 + 73 + 13 = 371 43 + 03 + 73 = 407 888 + 88 + 8 + 8 + 8 = 1 000 |
|
49 = 7² 4489 = 67² 444889 = 667² 44448889 = 6667² 4444488889 = 66667² |
10 89×9 = 98 01 10 9 89×9 = 98 9 01 10 99 89×9 = 98 99 01 10 999 89×9 = 98 999 01 10 9999 89×9 = 98 9999 01 |
21 78×4 = 87 12 21 9 78×4 = 87 9 12 21 99 78×4 = 87 99 12 21 999 78×4 = 87 999 12 21 9999 78×4 = 87 9999 12 |
|
12² = 144 13² = 169 102² = 10404 103² = 10609 112² = 12544 113² = 12769 122² = 14884 |
21² = 441 31² = 961 201² = 40401 301² = 90601 211² = 44521 311² = 96721 221² = 48841 |
3× 37 = 111 6× 37 = 222 9× 37 = 333 12× 37 = 444 15× 37 = 555 18× 37 = 666 21× 37 = 777 24× 37 = 888 27× 37 = 999 |
|
1× 91 = 0 9 1 2× 91 = 1 8 2 3× 91 = 2 7 3 4× 91 = 3 6 4 5× 91 = 4 5 5 6× 91 = 5 4 6 7× 91 = 6 3 7 8× 91 = 7 2 8 9× 91 = 8 1 9 |
37× 91 = 3367 33× 3367 = 111 111 66× 3367 = 222 222 99× 3367 = 333 333 132× 3367 = 444 444 165× 3367 = 555 555 198× 3367 = 666 666 231× 3367 = 777 777 264× 3367 = 888 888 297× 3367 = 999 999 |
1× 8 + 1 = 9 12× 8 + 2 = 98 123× 8 + 3 = 987 1234× 8 + 4 = 9876 12345× 8 + 5 = 98765 123456× 8 + 6 = 987654 1234567× 8 + 7 = 9876543 12345678× 8 + 8 = 98765432 123456789× 8 + 9 = 987654321 |
|
12 345 679× 9 = 111 111 111 12 345 679× 18 = 222 222 222 12 345 679× 27 = 333 333 333 12 345 679× 36 = 444 444 444 12 345 679× 45 = 555 555 555 12 345 679× 54 = 666 666 666 12 345 679× 63 = 777 777 777 12 345 679× 72 = 888 888 888 12 345 679× 81 = 999 999 999 |
7 × 15 873 = 111 111 7 × 31 746 = 222 222 7 × 47 619 = 333 333 7 × 63 492 = 444 444 7 × 79 365 = 555 555 7 × 95 238 = 666 666 7 × 111 111 = 777 777 7 × 126 984 = 888 888 7 × 142 857 = 999 999 |
7 × 143 = 1001 7 × 286 = 2002 7 × 429 = 3003 7 × 572 = 4004 7 × 715 = 5005 7 × 858 = 6006 7 × 1001 = 7007 7 × 1144 = 8008 7 × 1287 = 9009 |
|
3 × 8 547 × 13 = 333 333 4 × 8 547 × 13 = 444 444 5 × 8 547 × 13 = 555 555 9 × 8 547 × 13 = 999 999 |
13 × 3 × 7 × 13 × 37 = 131 313 27 × 3 × 7 × 13 × 37 = 272 727 52 × 3 × 7 × 13 × 37 = 525 252 89 × 3 × 7 × 13 × 37 = 898 252 |
185 × 7 × 11 × 13 = 185 185 259 × 7 × 11 × 13 = 259 259 327 × 7 × 11 × 13 = 327 327 467 × 7 × 11 × 13 = 467 467 |
|
6× 9 = 54 66× 99 = 6 534 666× 999 = 665 334 6 666× 9 999 = 66 653 334 66 666× 99 999 = 6 666 533 334 666 666× 999 999 = 666 665 333 334 6 666 666× 9 999 999 = 66 666 653 333 334 66 666 666× 99 999 999 = 6 666 666 533 333 334 666 666 666× 999 999 999 = 666 666 665 333 333 334 |
3 367 × 00 = 000 000 3 367 × 33 = 111 111 3 367 × 66 = 222 222 3 367 × 99 = 333 333 3 367 × 132 = 444 444 3 367 × 165 = 555 555 3 367 × 198 = 666 666 3 367 × 231 = 777 777 3 367 × 264 = 888 888 3 367 × 297 = 999 999 |
37× 0 = 000 37× 3 = 111 37× 6 = 222 37× 9 = 333 37× 12 = 444 37× 15 = 555 37× 18 = 666 37× 21 = 777 37× 24 = 888 37× 27 = 999 |
|
\frac{1}{99^{2}}=\frac{1}{9 \ 801} =0,00 \ 01 \ 02 \ 03 \ 04 \ 05 \ 06 \ 07 \ 08 \ 09 \\ 10 \ 11 \ 12 \ 13 \ 14 \ 15 \ 16 \ 17 \ 18 \ 19 \ 20 \ 21 \ 22 \ 23 \ 24 \\ 25 \ 26 \ 27 \ 28 \ 29 \ 30 \ 31 \ 32 \ 33 \ 34 \ 35 \ 36 \ 37 \ 38 \ 39 \\ 40 \ 41 \ 42 \ 43 \ 44 \ 45 \ 46 \ 47 \ 48 \ 49...
Après 99 les retenues brisent la régularité de la suite. Voici la parade : \frac{1}{999^{2}}=\frac{1}{998\ 001} = 0.000 \ 001 \ 002 \ 003 \ 004 \ 005 \ 006 \ 007 \ 008 \ 009 \ 010 \\ 011 \ 012 \ 013 \ 014 \ 015 \ 016 \ 017 \ 018 \ 019 \ 020 \\ 021 \ 022 \ 023 \ 024 \ 025 \ 026 \ 027 \ 028 \ 029 \ 030 \\ 031 \ 032...
Vous obtenez tous les nombres à trois chiffres de 000 à 999, dans l’ordre, à l’exception de 998. |
\frac{2}{9}=0,222 ... \\ \ \\ \frac{6}{99}=0,06 \ 06 \ 06 ... \\ \ \\ \frac{64}{99}=0,64 \ 64 \ 64 ...\\ \ \\\frac{123}{999}=0,123\ 123\ 123... \\ \ \\ \frac{789 456}{9999}=0,789456 \ 789456 \ 789456 ... \\
Si vous prenez un nombre n composé de k chiffres et que vous le divisez par un nombre composé de k chiffres 9, la partie décimale du nombre obtenu est une répétition de n. |
1 x 33² = 1089 2 x 33² = 2178 3 x 33² = 3267 4 x 33² = 4356 5 x 33² = 5445 6 x 33² = 6534 7 x 33² = 7623 8 x 33² = 8712 9 x 33² = 9801 |
|
111 111 111² = 12 345 678 987 654 321 1/998 001 = 1,002 003 004 005 006 |
1/7 = 0,142857 142857 142857 2/7 = 0,2857 142857 142857 3/7 = 0,42857 142857 142857 4/7 = 0,57 142857 142857 5/7 = 0,7 142857 142857 6/7 = 0,857 142857 142857 |
13 + 53 +33 = 153 163 + 503 + 333 = 165033 1663 + 5003 + 3333 = 166500333 16663 + 50003 +33333 = 166650003333 166663 + 500003 + 333333 = 166665000033333 |
|
6 × 7 = 42 66 × 67 = 4 422 666 × 667 = 444 222 666 666 × 666 667 = 444 444 222 222 666 666 666× 666 666 667 = 444 444 444 222 222 222 |
Le nombre 179999999999999999917 est un nombre premier constitué de 17 neuf entourés de deux 17. |
27 × 37 = 999 Mais aussi : 1/27 = 0,37 037 037 037 037… 1/37 = 0,27 027 027 027 027… |
|
\frac{10 100}{970 / 299} = 0,01 04 09 16 25 36 49 64 82 … Mais oui, les décimales nous montrent les 8 premiers carrés dans l’ordre. |
\frac{1}{998} = 0,001 002 004 008 016 032 064 128 256 513 … Voici les 9 premières puissances de 2 dans les décimales. |
\frac{100}{9 / 899} = 0,01 01 02 03 05 08 13 21 34 55 … \frac{1 000}{998 / 999} = 0,001 001 002 003 005 008 013 021 034 055 … \frac{10 000}{99 / 989 / 999} = 0,0001 0001 0002 0003 0005 0008 0013 0021 0034 0055 0089 0144 0233 … Voici maintenant la suite de Fibonacci dans les décimales. |
B°/ Un peu de calcul mental : Utilisons 4 fois le même chiffre
En utilisant 4 fois le même chiffre, des parenthèses et les 4 opérations, comment écrire les nombres proposés (les nombres non proposés sont impossibles).
| Le chiffre 1 :
1 = 1 × 1 × 1 × 1 2 = 1 × 1 + 1 × 1 3 = 1 × 1 + 1 + 1 4 = 1 + 1 + 1 + 1 |
Le chiffre 2 :
0 = 2 – 2 + 2 – 2 |
Le chiffre 3 :
0 = 3 – 3 + 3 – 3 |
| Le chiffre 4 :
0 = 4 – 4 + 4 – 4 = 4 + 4 – 4 – 4 = (4 – 4)x(4 + 4) |
Le chiffre 5 :
0 = 5 – 5 + 5 – 5 |
Le chiffre 6 :
0 = 6 – 6 + 6 – 6 |
| Le chiffre 7 :
0 = 7 – 7 + 7 – 7 |
Le chiffre 8 :
0 = 8 – 8 + 8 – 8 |
Le chiffre 9 :
0 = 9 – 9 + 9 – 9 |
Un autre jeu consiste à utiliser 4 fois le chiffre 4 pour obtenir tout les nombres entiers :
Remarque : .4 signifie 0,4 ce qui est un peu de la triche … et \bar{.4}= 0,44444... =\frac{4}{9}
| 0 = 4 ÷ 4 – 4 ÷ 4 = 44 – 44 | 26 = 4!+ v4 + 4 – 4 | 52 = 44 + 4 + 4 | 78 = 4(4! – 4 ) – v4 |
| 1 = 4 ÷ 4 + 4 – 4 = 44 ÷ 44 | 27 = 4!+ v4 + (4 ÷ 4) | 53 = 4! + 4! + 4 / .4 | 79 = \frac{4!-\sqrt{4} }{.4}+4! |
| 2 = 4 -(4 + 4)÷ 4 = (44 + 4) ÷ 4! | 28 = (4 + 4)×4 – 4 = 4!+ 4 + 4 – 4 | 54 = 4! + 4! + (4! / 4) | 80 = 4! × 4 – 4×4 |
| 3 = (4 × 4 – 4)÷ 4 = (4 + 4 + 4) ÷ 4 | 29 = 4!+ 4 + (4 ÷ 4) | 55 = 4! / .4 – 4 / .4 | 81 = \left(4 - \frac{4}{4}\right) ^{4} |
| 4 = 4 + 4 ×(4 – 4) = -44 + 4! + 4! | 30 = 4!+ 4 + 4 – v4 | 56 = 44 + 4! / v4 | 82 = 4! / .4 + 4! – v4 |
| 5 = (4 × 4 + 4)÷ 4 = (44 – 4!) ÷ 4 | 31 = 4!+ (4! + 4) ÷ 4 | 57 = (4! – 4) / .4 + 4 | 83 = \frac{4! - .4}{.4} + 4! |
| 6 = (4 + 4)÷ 4 + 4 | 32 = 4 x 4 + 4 x 4 | 58 = (4! + 4) v4 +v4 | 84 = 4! × 4 – 4! / v4 |
| 7 = 4 + 4 – 4 ÷ 4 = 44 ÷ 4 – 4 | 33 = (4 – .4)/.4 + 4! | 59 = 4!/.4 – 4/4 | 85 = \frac{4! + .4}{.4} + 4! |
| 8 = 4 ÷ 4 × 4 + 4 | 34 = 4! + 4! / 4 + 4 | 60 = 44 + 4 × 4 | 86 = 4! × 4 – 4/.4 |
| 9 = 4 ÷ 4 + 4 + 4 = 44 ÷ 4 – v4 | 35 = 44 / 4 + 4! | 61 = 4!/.4 + 4/4 | 87 = \frac{4! + 4}{\bar{.4} } + 4! |
| 10 = 4 ÷v4 + 4 ×v4 = (44 – 4) ÷ 4 | 36 = 44 – 4 – 4 | 62 = (4 + 4) ^ v4 – v4 | 88 = 4! × 4 – 4 – 4 |
| 11 = (4!×v4 – 4)÷ 4 = 44 / (v4 + v4) | 37 = (v4 + 4!)/v4 + 4! | 63 = (44 – 4) / 4 = (4! + v4) / .4 – v4 | 89 = 4! + (4! + v4) / .4 |
| 12 = 4 ×(4 – 4 ÷ 4) = (44 + 4) ÷ 4 | 38 = 44 – 4!/4 | 64 = 4 × 4 × v4 × v4 | 90 = 4! × 4 – 4! / 4 |
| 13 = (4!×v4 + 4)÷ 4 = 44 ÷ 4 + v4 | 39 = 4! + (4 + 4/4)!! = (4 × 4 – .4)/.4 | 65 = (4^4 +4) / 4 | 91 = 4 × 4! – v4 / .4 |
| 14 = 4 × 4 – 4 ÷v4 = 4 × (v4 + v4) – v4 | 40 = 44 – v(4 × 4) | 66 = (4 + 4) ^ (v4) + v4 | 92 = 4! × (v4 + v4) – 4 |
| 15 = 4 × 4 – 4 ÷ 4 = 44 ÷ 4 + 4 | 41 = (v4 + 4!)/.4 – 4! | 67 = (4! + v4) / .4 + v4 | 93 = \frac{\sqrt{4} +\frac{4!}{.4} }{\sqrt{\bar{.4} } } |
| 16 = 4 × 4 + 4 – 4 | 42 = v4 + 44 – 4 | 68 = (4 + 4) ^ v4 + 4 | 94 = 4! × 4 – 4/v4 |
| 17 = 4 × 4 + 4 ÷ 4 = (44 + 4!)÷ 4 | 43 = 44 – 4/4 | 69 = (4! + 4 – .4) / .4 | 95 = 4! × 4 – 4/4 |
| 18 = 4 × 4 + 4 -v4 = (44 ÷ v4) – 4 | 44 = 44 + 4 – 4 | 70 = (4 + 4)! / (4! x 4!) = 44 + 4! + v4 | 96 = 4! × 4 + 4 – 4 |
| 19 = 4!-(4 + 4 ÷ 4) | 45 = 4/4 + 44 | 71 = (4 + 4! + .4) / .4 | 97 = 4! × 4 + 4/4 |
| 20 = 4 ×(4 + 4 ÷ 4) = (44 – 4) ÷ v4 | 46 = 44 – v4 + 4 | 72 = (4! / 4) ^ v4 × v4 | 98 = 4! × 4 + 4/v4 |
| 21 = 4!- 4 + 4 ÷ 4 = (44 – v4) ÷ v4 | 47 = 4! + 4! – 4/4 | 73 = \sqrt{\sqrt{\sqrt{4^{4!} } } } +\frac{4}{\bar{.4}} | 99 = \frac{4 + .4}{\bar{.4}-.4 } |
| 22 = 4!÷ 4 + 4 × 4 = 44 ÷ (4 – v4) | 48 = 4 × (4 + 4 + 4) | 74 = 4! + 4! + 4! + v4 | 100 = 4! × 4 + v4 + v4 |
| 23 = 4!+ 4 ÷ 4 -v4 = (44 + v4) ÷ v4 | 49 = 4! + 4! + 4 / 4 | 75 = (4! + v4 + 4) / .4 | |
| 24 = 4 × 4 + 4 + 4 = (44 + 4) ÷ v4 | 50 = 4! / 4 + 44 | 76 = 4! × 4 – 4! + 4 | |
| 25 = 4!- 4 ÷ 4 +v4 | 51 = (4! – 4 + .4) / .4 | 77 = \left(\sqrt{\frac{4}{\bar{.4}} } \right) ^{4}-4 |
Source : http://villemin.gerard.free.fr/Wwwgvmm/Formes/Quatre4p.htm
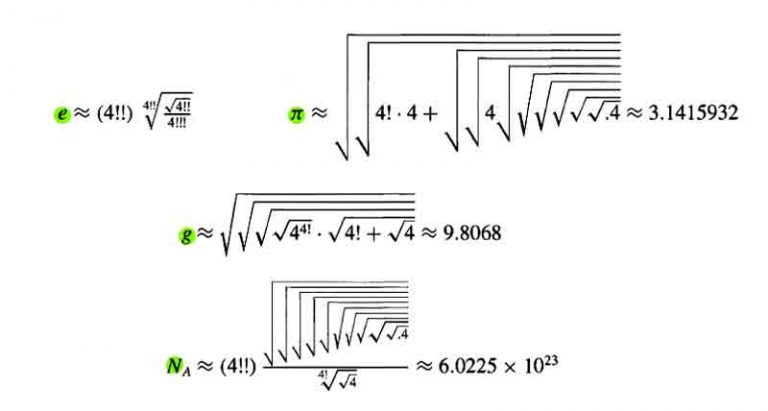 |
Quatre constantes fondamentales dans quatre 4 : En 2001, une équipe de mathématiciens du Harvey Mudd College a découvert que nous pouvions même obtenir quatre 4 pour approximer quatre constantes notables : le nombre e , π , l’accélération de la gravité g et le nombre d’Avogadro . |
C°/ 666 un nombre maléfique et le nombre de Belphégor :
- Les numérologues considèrent que le nombre 666 est maléfique, aussi le remplacent-ils par de jolies combinaisons.
Ainsi : 666 = 6 + 6 + 6 + 633+ 633 + 633.
- C’est aussi la somme des sept premiers nombres premiers au carré : 666 = 2² + 3² + 5² + 7² + 11² + 13² + 17².
- C’est un nombre triangulaire : 666 = 1 + 2 + 3 + … + 36
- C’est par ailleurs un nombre palindromique c’est à dire qu’il peut se lire de droite à gauche ou de gauche à droite.
- Mais le 13 est aussi un nombre maléfique, notamment pour la religion chrétienne. Alors les mathématiciens ce sont amusés à créer le nombre de Belphégor qui est constitué du nombre 666 précédé de 13 zéros et suivit de 13 zéros, avec un 1 au début et à la fin : 1 000 000 000 000 066 600 000 000 000 001. Ce nombre est un palindrome et aussi un nombre premier, sa notation est le nombre \pi écrit à l’envers.
- Si l’on translittère la forme grecque Καίσαρ Νέρων du nom de l’empereur Caesar-Neron en hébreu קסר נרון suivant la guématria, la valeur numérique de l’addition de l’ensemble des lettres donne 666 dans un nombre qui, par opposition au chiffre 7 qui symbolise la perfection, symbolise l’imperfection suprême; si on translittère la forme latine « Caesar-Nero » en l’hébreu קסר נרו cela donne 616.
- Les ennemis du pape ce sont aussi prêtés à ce petit jeux des nombres. Le pape est le vicaire de dieu ce qui donne en latin :
VICarIVs fILII DeI en ne prenant que les lettre traduisibles en nombre = 5 + 1 + 100 + 1 + 5 + 1 + 50 + 1 + 1 + 500 + 1 = 666 - Hitler aussi peut donner 666 si on considère que le A = 100; B = 101; C = 103.
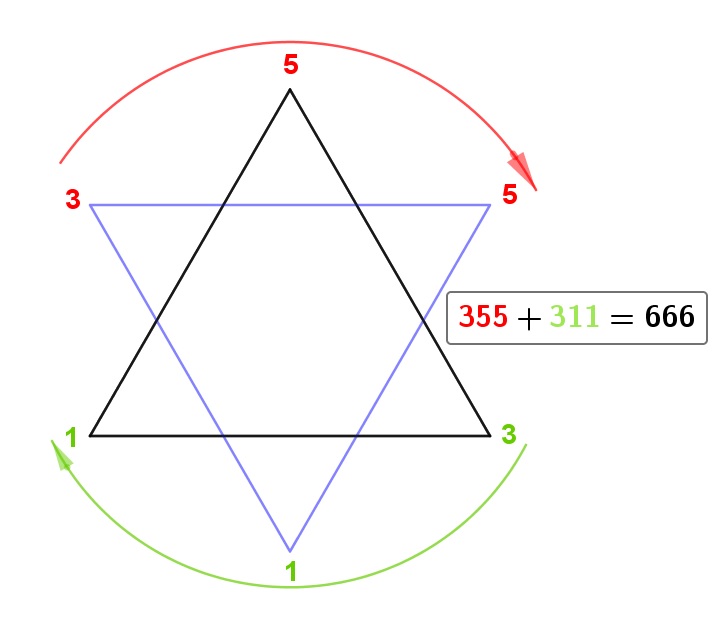
En effet : H = 107 + I = 108 + T = 119 + L = 111 + E = 104 + R = 117 = 666 - Dans la bible : bien entendu le nombre de la bête est présent dans la bible car la bête représente le diable. Dans les Évangiles selon St Jean : les disciples pêchent et sortent 153 poissons.
Plaçons les chiffres 1, 5 et 3 dans un triangle équilatéral noir dans le sens des aiguilles d’une montre, et dans un autre triangle équilatéral bleu dans le sens inverse. On obtient l’étoile de David. Si on additionne les nombres composés par 3 chiffres dans un sens et dans l’autre, on trouve 666 à chaque fois !!!
 |
 |
 |
Petite remarque assez troublante : si on prend les 3 chiffres du haut de l’étoile, c’est à dire 355, et que l’on divise par ceux du bas, c’est à dire 113, et bien on obtient une approximation du nombre \pi à 6 décimales près … \frac{355}{113} = 3,14159292 \approx \pi
Toujours dans l’Apocalypse de Jean, chapitre 13, versets 11 à 18, on présente la bête, monstre de la fin du monde, et son nombre.
Puis je vis monter de la terre une autre bête, qui avait deux cornes semblables à celles d’un agneau, et qui parlait comme un dragon. […] Que celui qui a de l’intelligence calcule le nombre de la bête. Car c’est un nombre d’homme, et son nombre est six cent soixante-six.
D°/ Somme des n premiers nombres entiers impairs = n² :
De façon générale la somme des n premiers nombres impairs est n².
En effet la suite arithmétique des n premier nombre impair donne :
Avec : Premier terme : u1 = 1
Dernier terme : un = 2n – 1
Nombre de termes : n
Exemple. La somme des 4 premiers nombres impairs est le carré de 4, soit 16 : 1 + 3 + 5 + 7 = 4² = 16
|
La démonstration est plus jolie si on commence avec u0 = 1 \large{ 1+3+5+...+(2n+1)=\frac{(n+1)(u_{1}+u_{n})}{2}=\frac{(n+1)(1+2n+1)}{2}=\frac{(n+1)(2n+2)}{2}=(n+1)^{2}}
Avec : Premier terme : u0 = 1 Dernier terme : un = 2n + 1 Nombre de termes : n+1 Exemple. La somme des 4 premiers nombres impairs avec n=3 est le carré de 4, soit 16 : 1 + 3 + 5 + 7 = (3+1)² = 16 |
E°/ Somme des n premiers carrés = n (n+1) (2n+1) / 6 :
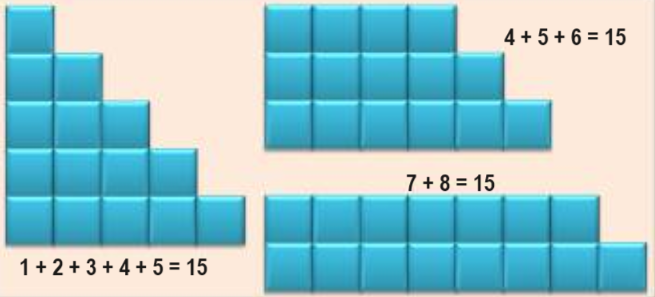
Commençons par les 4 premiers carrés : 12 + 22 + 32 + 42 = ( 4 x 5 x 9 ) / 6 = 30
Pour cela constituons un pyramidal en empilant quatre étages de forme carrés.
Nous avons un carré de 1 case, puis un carré de 2² = 4 cases, puis de 3² = 9 cases et enfin de 4² = 16 cases.
Maintenant, comme dans un puzzle 3D, agençons six pyramidaux pour reconstituer un parallélépipède rectangle de dimensions 4, 5 et (2 x 4 + 1 =) 9. Nous obtenons alors : 12 + 22 + 32 + 42 = ( 4 x 5 x 9 ) / 6 = 30 cubes.
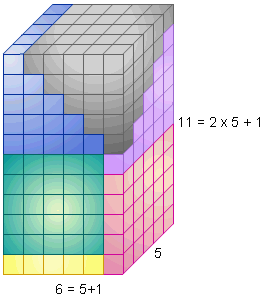 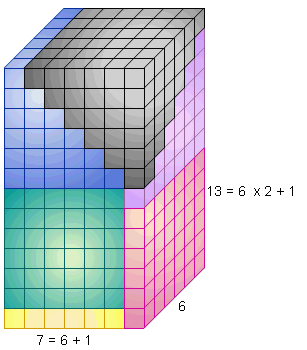 |
De même agençons six pyramidaux constitués de carrés de 1 à 5² cases. Nous obtenons un parallélépipède de dimensions 5, 6 et (2 x 5 + 1 =) 11.
Somme des carrés des 5 premiers entiers Somme des carrés des 6 premiers entiers
12 + 22 + 32 + 42 + 52 = ( 5 x 6 x 11 ) / 6 12 + 22 + 32 + 42 + 52 + 62= ( 6 x 7 x 13 ) / 6
Le procédé se généralise avec un pyramidal obtenu en empilant des carrés de 1 à n² cases.
Six pyramidaux réunis permettent de construire un parallélépipède de dimensions n, n+1 et 2n+1.
Nous obtenons le résultat général :
12 + 22 + 32 + 42 + 52 + 62 + 72 +… + n2 = n (n+1) (2n+1) / 6
F°/ Le cube de la somme de deux nombres : (a+b)³
| Le grand cube dont les côtés mesurent (a + b) a un volume de (a+b)(a+b)(a+b)=(a+b)³ Il est composé : .du cube d’arête a et de volume a³, .des 3 parallélépipèdes rectangles de côtés a, a et b de volumes ba² chacun, .des 3 parallélépipèdes rectangles de côtés a, b et b de volumes ab² chacun, .du cube d’arête b et de volume b³.Donc (a+b)³= a³ + 3ba²+ 3ab² + b³Par le calcul, nous avons bien : (a+b)3 = (a + b)2 (a + b) (a+b)3 =(a2 + 2ab + b2 )(a + b) (a+b)3 = a3 + 2a2b + b2a + a2b + 2ab2 + b3 (a+b)3 = a3 + 3a2b + 3ab2 + b3 |
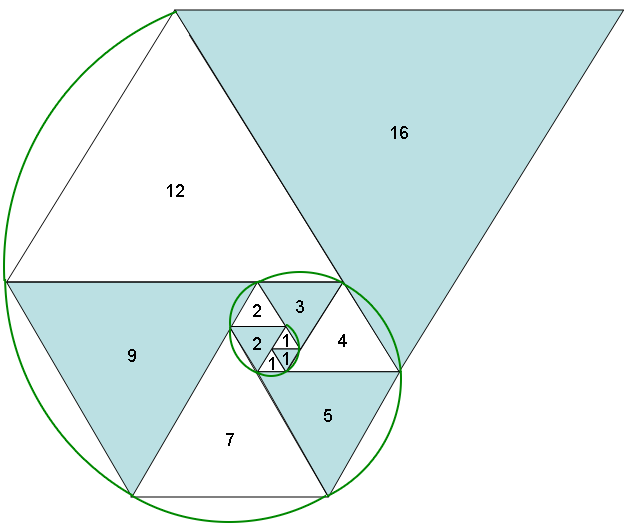
G°/ Théorème de Nicomaque : la somme des n premiers cubes = (1 + 2 + 3 + 4 + 5 + 6 + 7 + … + n )2
13 + 23 + 33 + 43 + 53 + 63 + 73 +… + n3 = (1 + 2 + 3 + 4 + 5 + 6 + 7 + … + n )2
En effet, si l’on décompose correctement le cube de chaque entier, nous pouvons retrouver facilement la somme des cubes de différents entiers.
Découvrons d’emblée les résultats sur l’animation ci-dessous : le volume de chaque cube est égal à l’aire d’une zone colorée dans le même ton.
Voyons maintenant pourquoi l’aire de chaque zone colorée correspond bien au volume d’un cube. Nous connaissons la somme des entiers naturels de 1 à n avec la formule :
1+2+3+4+...+n = \frac{n(u_{1}+u_{n})}{2}= \frac{n(1+n)}{2}Nous en déduisons que pour chaque valeur de l’entier n :
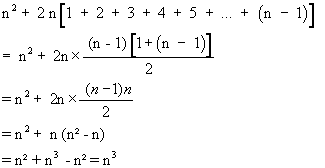
Au final, on obtient un carré de côté (1 + 2 + 3 + 4 + 5 + 6 + 7 + … + n ) et donc de surface (1 + 2 + 3 + 4 + 5 + 6 + 7 + … + n )².
H°/ Les nombres Phénix :
Le bestiaire des nombres recèlent de bien curieux phénomènes…
Très curieux sont en effet les nombres phénix, qui comme leur nom l’indique peuvent renaître de leurs cendres!! Comment ?
En voici un exemple : le nombre 052 631 578 947 368 421 (à vos souhaits) est un de ces nombres si étranges.
Vous pouvez essayer de le multiplier par tout nombre entier compris entre 2 et 18, vous ne retrouverez bien sûr pas notre nombre de départ, mais les chiffres du résultat se suivent exactement dans le même ordre, à un décalage près !!!
exemple : si on le multiplie par deux, on obtient 1 052 631 578 947 368 42. le dernier 1 du nombre de départ s’est retrouvé en tête du nombre d’arrivée !! Pour le moins étonnant !!
Mais celui-ci vous réserve une autre surprise: multipliez-le donc par 19 pour comprendre à quel point ce nombre est « magique »…… :
52 631 578 947 368 421 x 19 = 999 999 999 999 999 999
Et le plus étonnant est qu’il existe d’autres nombres ayant les mêmes propriétés comme 0 588 235 294 117 647 ou 142 857 !!
|
142 857 × 2 = 285 714 142 857 × 3 = 428 571 142 857 × 4 = 571 428 142 857 × 5 = 714 285 142 857 × 6 = 857 142 142 857 × 7 = 999 999 |
L’explication est assez simple : 142 857 est la période de 1/7 \frac{1}{7} = 0,142 \ 857 \ 142 857 \ \overline{142 857} ...142 \ 857 = 0,142 \ 857 \times 1 000 000 = \frac{0,999 \ 999}{7}\times 1 000 000 = \frac{999 \ 999}{7} \\Donc : 142 \ 857 \times 7 = \frac{999 \ 999}{7} \times 7 = 999 \ 999 |
La règle générale : 0,052 631 578 947 368 421 = 1/19 donc 052 631 578 947 368 421 x 19 = 999 999 999 999 999 999
0,0 588 235 294 117 647 = 1/17 donc 0 588 235 294 117 647 x 17 = 9 999 999 999 999 999
0,142 857 = 1/7 donc 142 857 × 7 = 999 999
I°/ Les nombres remarquables :
https://oeis.org/ ou https://www.math93.com/index.php/histoire-des-maths/histoire-des-nombres/158-les-nombres-remarquables
Les Mathématiciens adorent jouer avec les nombres et adorent encore plus les classer. Voici quelques nombres au titre poétique ou amusant comme nombres amicaux, parfaits ou de poulet.
Sur ce site vous pourrez tout connaitre d’un nombre : http://www.numbergossip.com/
| Nom des nombres | Définition | Exemple | La liste de ces nombres | ||||||||
| Les nombres abondants | Nombre entier naturel non nul qui est strictement inférieur à la somme de ses diviseurs stricts sauf lui-même. | 12 : La somme de ces diviseurs 1 + 2 + 3 + 4 + 6 = 16 > 12 | https://oeis.org/A005101 | ||||||||
| Les nombres autobiographiques |
Nombre entier positif dont le 1er chiffre indique le nombre de 0 contenus dans ce nombre, le 2e le nombre de 1, le 3e le nombre de 2 et ainsi de suite jusqu’au 10e qui doit indiquer le nombre de 9 dans ce nombre. |
1210 est le plus petit d’entre eux (1 chiffre 0, 2 chiffres 1, 1 chiffre 2 et 0 chiffre 3). |
https://oeis.org/A046043 | ||||||||
| Les nombres déficients | Nombre entier naturel non nul qui est strictement supérieur à la somme de ses diviseurs stricts sauf lui-même. | 10 : La somme de ces diviseurs 1 + 2 + 5 = 8 < 10 | https://oeis.org/A005100 | ||||||||
| Les nombres parfaits | Nombres qui sont égaux à la somme de leurs diviseurs entiers naturels sauf eux-mêmes. On en connaît 48, dont huit inférieurs à 1021. | 28 : La somme de ces diviseurs 1 + 2 + 4 + 7 + 14 = 28 | https://oeis.org/A000396 | ||||||||
| Les nombres amicaux ou amiables | Couple d’entiers naturels dont la somme de diviseurs stricts, autre que lui-même, de l’un est égale à la somme de diviseurs stricts de l’autre. | La paire (220,284) est amiable et c’est la première. Les Grecs ne connaissaient que celle-ci.
La somme des diviseurs propres de 220 : 2+4+5+11+22+55+44+20+110+10+1 = 284. La somme des diviseurs propres de 284 : 2+4+71+142+1 = 220 |
https://oeis.org/A063990 | ||||||||
| Les nombres sociables | Suite de nombres qui sont la somme des diviseurs propres du nombre précédent (en revenant sur le premier). |
Par exemples : 1264460, 1547860, 1727636, 1305184 (1547860 est la somme de tous les diviseurs propres de 1264460 …) Une suite de 28 nombres sociables : 14316 → 19116 → 31704 → 47616 → 83328 → 177792 → 295488 → 629072 → 589786 → 294896 → 358336 → 418904 → 366556 → 274924 → 275444 → 243760 → 376736 → 381 028 → 285 778 → 152990 → 122410 → 97946 → 48976 → 45946 → 22976 → |
Un outil pour les calculer. |
||||||||
| Les nombres chanceux | Nombres entiers naturels obtenus de la façon suivante :
On commence avec la suite d’entiers démarrant par 1 : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Puis on enlève un nombre sur deux, ce qui ne laisse que les entiers impairs : 1 3 5 7 9 11 13 15 17 19 21 23 25 Le deuxième terme de la suite est désormais 3. Ensuite, on enlève un nombre sur trois parmi ceux qui restent dans la liste : 1 3 7 9 13 15 19 21 25 Le troisième nombre survivant est 7. On enlève alors un nombre sur sept parmi ceux qui restent dans la liste : 1 3 7 9 13 15 21 25 Le quatrième nombre survivant est 9. Puis on enlève un nombre sur neuf parmi ceux qui restent dans la liste, etc. Si l’on répète cette procédure indéfiniment, les survivants sont les nombres chanceux : 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, … |
1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, … | https://oeis.org/A000959 | ||||||||
| Les nombres heureux (happy nomber) | Entier naturel tel que si on calcule la somme des carrés de ses chiffres puis la somme des carrés des chiffres du nombre obtenu et ainsi de suite, on aboutit au nombre 1. |
19 est un nombre heureux car : 1² + 9² = 82 |
https://oeis.org/A007770 | ||||||||
| Les nombres malheureux (unhappy nomber) | Entier naturel tel que si on calcule la somme des carrés de ses chiffres puis la somme des carrés des chiffres du nombre obtenu et ainsi de suite, il boucle sur le cycle long |
14 est un nombre malheureux car :
|
https://oeis.org/A031177 | ||||||||
| Les nombres de Harshad | Du sanskrit « harṣa » (« joie ») et « da » (« qui donne »). Nombres divisiblent par la somme de ses chiffres. |
2022 est divisible par la somme 2+2+0+2 = 6. 2022/6 = 337 |
https://oeis.org/A005349 | ||||||||
| Les nombres taxicab | Nombre qui peut être exprimé comme la somme de deux cubes, de plusieurs façons différentes (en l’occurrence, 2).
Godfrey Harold Hardy, mathématicien britannique de la première moitié du XXe siècle, rapporte l’anecdote suivante, concernant le mathématicien indien Srinivasa Ramanujan :« Je me souviens que j’allais le voir une fois, alors qu’il était malade, à Putney. J’avais pris un taxi portant le numéro 1729 et je remarquai que ce nombre me semblait peu intéressant, ajoutant que j’espérais que ce ne fût pas mauvais signe. |
1729 = 13 + 123 = 93 + 103 | https://oeis.org/A011541 | ||||||||
| Les nombres poulet
https://fr.wikipedia.org/wiki/Nombre_et_supernombre_de_Poulet |
En arithmétique, un test de primalité courant pour un nombre impair n consiste à tester si n divise 2n – 2 : dans le cas contraire, en vertu de la contraposée du petit théorème de Fermat, on conclut que n n’est pas premier. Cependant il existe des nombres composés qui passent ce test avec succès : on les appelle nombres de Poulet, en l’honneur de Paul Poulet qui en a listé en 1926, ou nombres de Sarrus, car F. Sarrus découvrit certains de ces nombres (comme 341) en 18191.
Un nombre composé n est donc un nombre de Poulet si n divise 2n – 2, autrement dit si c’est un nombre faiblement pseudo-premier en base 2. Un supernombre de Poulet est un nombre composé dont tous les diviseurs composés sont des nombres de Poulet (ces diviseurs sont alors aussi des supernombres de Poulet), ou encore : un nombre composé dont chaque diviseur d divise 2d – 2. |
2341 – 2 est divisible par 341 | https://oeis.org/A001567 | ||||||||
| Les nombres triangulaires | Nombres entiers naturels de la forme n(n+1)/2 , n étant un entier naturel. | t3 = 3+2+1 = 6 est le 3ième nombre triangulaire car 6 = 3(3+1)/2 | https://oeis.org/A000217 | ||||||||
| Les nombres univers | Nombre réel dans les décimales duquel on peut trouver n’importe quelle succession de chiffres de longueur finie.
Vous pouvez ainsi vérifier sur cette page, si votre date de naissance ou votre numéro de téléphone est présent dans les décimales de |
Même si ce n’est pas encore démontré, le nombre |
http://www.angio.net/pi/piquery | ||||||||
| Nombres Escaliers, Polis ou Trapézoïdaux |
C’est un nombre qui peut s’écrire sous la forme de une ou plusieurs sommes de deux ou plusieurs nombres consécutifs. |
|
https://oeis.org/A138591 | ||||||||
| Nombres cyclopes |
Un nombre cyclope possède un nombre impair de chiffres et son chiffre du milieu est 0. |
|
https://oeis.org/A134808 | ||||||||
| Nombres puissants |
Un entier naturel n est dit puissant si, pour tout diviseur premier p de n, le carré p2 divise également n. Cela signifie que dans la décomposition en facteurs premiers de n, tous les exposants sont supérieurs ou égaux à 2. |
6615 = 33 × 5 × 7² n’est pas puissant car pas divisible par 5² |
https://oeis.org/A001694 | ||||||||
| Nombres de Dudeney |
Un nombre de Dudeney est un entier positif dont la somme de ses chiffres décimaux est égale à la racine cubique du nombre. Il en existe seulement 7. |
\sqrt[3]{0}=0\\\sqrt[3]{1}=1\\\sqrt[3]{512}=5+1+2=8\\\sqrt[3]{4913}=4+9+1+3=17\\\sqrt[3]{5832}=5+8+3+2=18\\\sqrt[3]{17 576}=1+7+5+7+6=26\\\sqrt[3]{19 683}=1+9+6+8+3=27
|
https://oeis.org/A046459 | ||||||||
|
Un entier est dit k-rugueux s’il n’est divisible par aucun nombre premier inférieur à k. |
14 n’est pas 5-rugueux, car il est divisible par 2, un nombre premier inférieur à 5.
49 est 5-rugueux, car il n’est divisible ni par 2 ni par 3 (les nombres premiers inférieurs à 5). |
https://oeis.org/A007310 | |||||||||
| Nombres de Lychrel |
Si on ajoute un nombre entier et sont renversé (le même nombre écrit à l’envers), on obtient un nombre palindrome. |
143 + 341 = 484 nombre palindrome 196 est le plus petit candidats à la liste des nombres de Lychrel. |
https://oeis.org/A023108 | ||||||||
| Les nombres auto-biographiques ou auto-descriptifs | C’est un entier naturel dont le premier chiffre indique le nombre de 0 qu’il contient, le deuxième chiffre le nombre de 1, etc., en respectant l’ordre numérique. | 1210 :
|
https://oeis.org/A046043 |
J°/ La fonction 91 :
En 1970 le mathématicien John McCarthy, a proposée une fonction de calcul très simple mais avec un résultat assez surprenant.
Prenez un nombre entier inférieur ou égal à 101. Si ce nombre est plus grand à 100, enlever-lui 10, sinon ajouter 11. Puis recommencer jusqu’à indéfiniment. Vous tomberez obligatoirement sur le nombre 91 ….
En langage Mathématique cela donne :
f(n) = \left\{\begin{matrix}n-10 & si \ n > 100 \\ f(f(n+11)) & sinon\end{matrix}\right.Exemples : un programme SCRATCH pour tester.
f(99) = f(f(110)) car 99 ≤ 100
= f(100) car 110 > 100
= f(f(111)) car 100 ≤ 100
= f(101) car 111 > 100
= 91 car 101 > 100
|
f(87) = f(f(98))
= f(f(f(109)))
= f(f(99))
= f(f(f(110)))
= f(f(100))
= f(f(f(111)))
= f(f(101))
= f(91)
= f(f(102))
= f(92)
= f(f(103))
= f(93)
...
= f(99)
...
= 91
|
K°/ Les équations palindromiques :
– Un palindrome peut se lire de droite à gauche et inversement. Le nombre 12521 est un nombre palindrome.
Mais trouver des équations qui le soient est plus compliqué :
61 – (8 + 8 + 8 + 8 + 8) = (8 + 8 + 8 + 8 + 8) – 19 : on obtient 21.
98 x 99 – (609 + 6969 + 111) = (111 + 6969 + 609) – 66 x 86 : on obtient 2013.
– Une autre bizarrerie : prenez n’importe quel nombre, inversez ses chiffres et ajoutez-le au nombre d’origine. Répétez ce processus et vous finirez par obtenir un palindrome.
196 est le plus petit nombre pour lequel un palindrome n’a pas été trouvé par ce processus itératif.
| 13 + 31 = 44 | 127 + 721 = 848 | 486 + 684 = 1170 puis 1170 + 0711 = 1881 |
196 + 691 = 887 puis 887 + 788 = 1975 puis 1675 + 5761 = 7436 ….
L°/ Une jolie démonstration :
Tout nombre au carré peut s’écrire sous la forme de l’addition de deux nombres triangulaires.
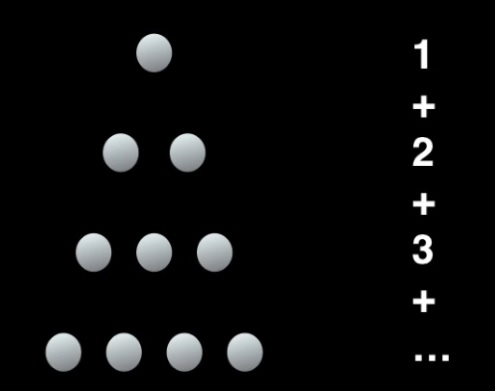 |
Pour rappel un nombre triangulaire de rang n noté tn, est la somme de tous les nombres de 1 jusqu’à n. On peut les représenter sous la forme d’un triangle de base n, d’où leur nom. Exemple : t5 = 1 + 2 + 3 + 4 + 5 = 15 |
 |
La démonstration est plutôt ardus, bien que tout à fait correcte. |
 |
Mais en modélisant le problème par un schémas, la solution est tout de suite plus évidente et même très simple. Commençons par représenter un carré comme 25 = 5², puis découpons le par une diagonale comme sur la figure ci-contre. Le triangle supérieur est un nombre triangulaire d’ordre 5 et le triangle inférieur d’ordre n-1. Ainsi : n² = tn + tn-1 |
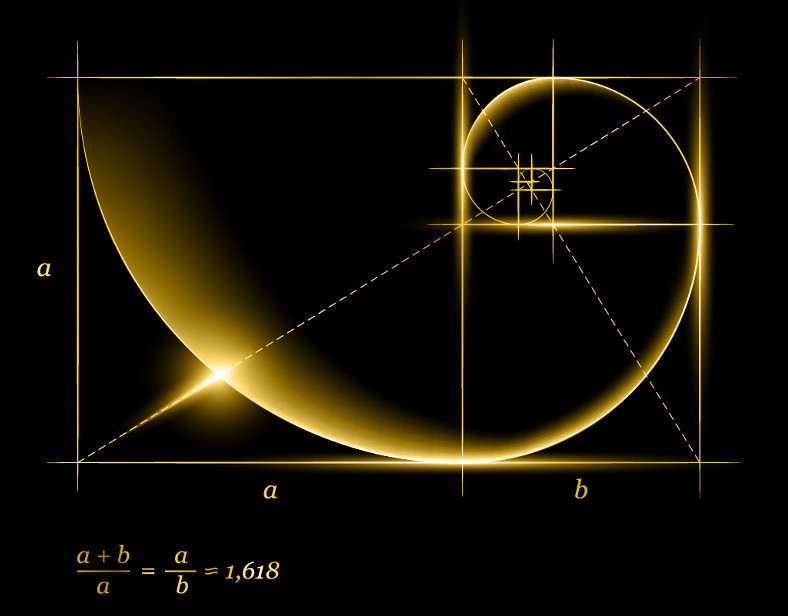
M°/ Le nombre d’or :
Un nombre mystérieux et magique dont on parle depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, …
Il caractérise l’harmonie et l’esthétique dans les arts, bien que certains lui reproche son caractère ésotérique.
On le désigne par la lettre grecque \varphi ( phi ) en hommage au sculpteur grec Phidias (490 – 430 avant J.C) qui décora le Parthénon à Athènes.
1°/ Son nom :
2°/ Sa définition :
3°/ Le rectangle d’or :
4°/ La spirale d’or :
5°/ Le triangle d’or :
6°/ Le pentagone d’or :
7°/ De bien belles formules :
8°/ Suite de Fibonacci :
9°/ Les suites :
10°/ Le nombre d’or est partout :
11°/ Rapports métalliques :
| Une superbe vidéo sur le nombre d’or dans la nature. |
Quel est le point commun entre un ananas, des lapins et la tour de Pise ? Le nombre d’or et la suite de Fibonacci. |
|
|
|
| El Jj démystifie le nombre d’or. |
|
1°/ Son nom : il a évolué avec le temps.
- Le mathématicien et moine franciscain Luca Pacioli (1445 ; 1517) parle de « Divine proportion »
- Le physicien Johannes Kepler (1571 ; 1630) le désigne comme le « joyau de la géométrie »
- Léonard de Vinci l’appelle la « section dorée »
- Le prince Matila Ghyka en 1932, diplomate et ingénieur, est le premier à parler de « nombre d’or ».
2°/ Sa définition : le nombre d’or est la solution positive de l’équation : x² – x – 1 = 0 et sa valeur est : \varphi =\frac{1+\sqrt{5}}{2} \approx 1,618033... .
Concrètement cela veut dire que si on le multiplie par lui-même on le retrouve additionné de 1 : \varphi ^{2}= \varphi+1
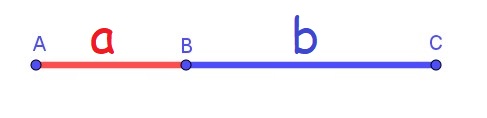 |
Peut-on trouver 2 segments alignés a et b tel que le rapport du plus grand sur le plus petit soit égal au rapport de la somme sur le plus grand ? \varphi=\frac{b}{a}=\frac{a+b}{b}=\frac{a}{b}+\frac{b}{b}=1+\frac{1}{\varphi}\Rightarrow\varphi=1+\frac{1}{\varphi} |
 |
Géométriquement, si on prend un segment de longueur a, qu’on le multiplie par \varphi puis encore par \varphi , le grand segment est la somme des 2 petits. C’est cette propriété qui rend les longueurs harmonieuses. |
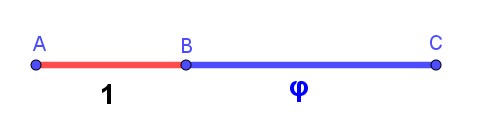 |
Autrement dit, 2 segments seront dans la proportion du nombre d’or si le rapport du grand sur le moyen est égal au rapport du moyen sur le petit. \frac{AC}{BC}=\frac{BC}{AB}\Rightarrow \frac{1+\varphi }{\varphi}=\frac{\varphi }{1}\Rightarrow 1+\varphi =\varphi ^{2}\Rightarrow \varphi ^{2}-\varphi -1 = 0 \\ \Delta = b^{2}-4ac = (-1)^{2}-4\times 1\times (-1) = 5 \\ \varphi_{1} =\frac{-b-\sqrt{\Delta }}{2a}=\frac{1-\sqrt{5}}{2}<0 \ impossible \ c'est \ une \ longueur \\ \varphi_{2} =\frac{-b+\sqrt{\Delta }}{2a}=\frac{1+\sqrt{5}}{2}>0 \ c'est \ la \ valaur \ de \ \varphi |
 |
Une autre façon de faire :
L’inverse de \varphi est noté \phi et il représente la partie décimale de \varphi . |
3°/ Le rectangle d’or : de largeur une unité et de longueur \varphi . Ces proportions sont esthétiquement parfaites et on le retrouve dans de nombreux bâtiments.
 |
Construction d’un rectangle d’or :
|
De façon générale, un rectangle est d’or si le rapport de sa longueur sur sa largeur est égal à \varphi .
|
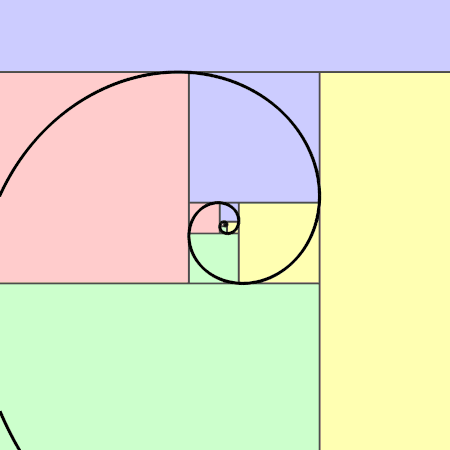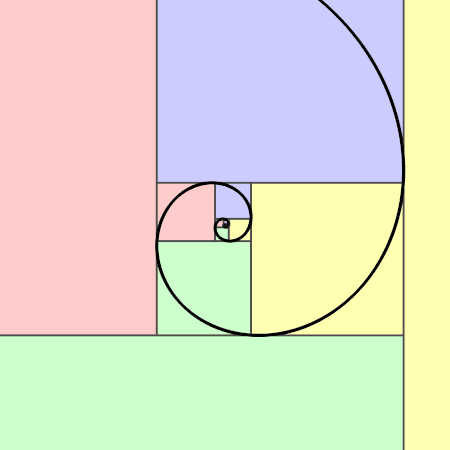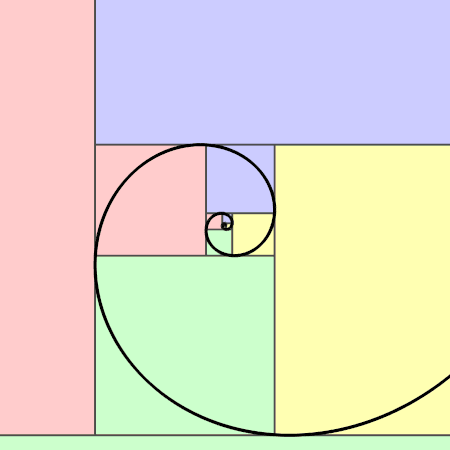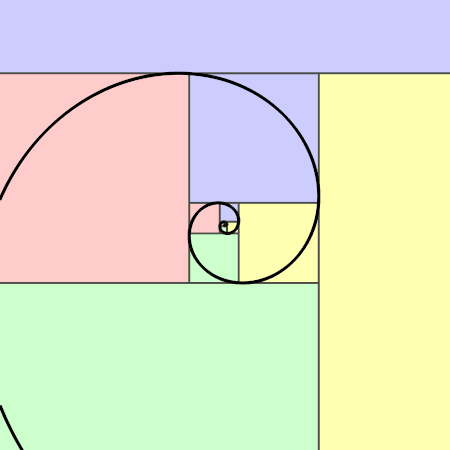
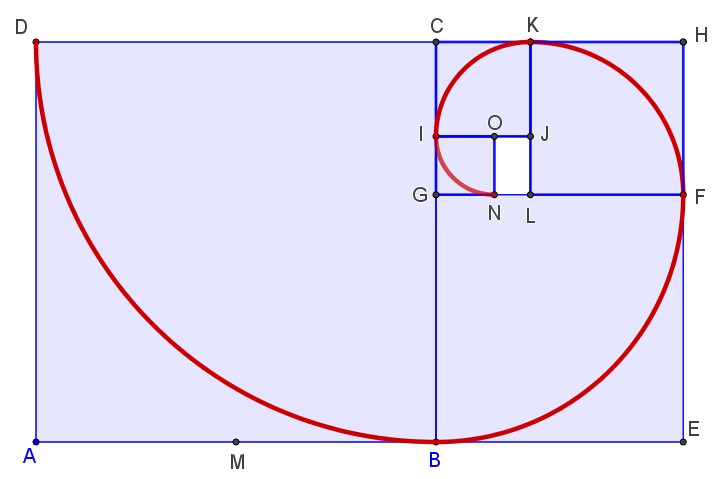
A partir d’un rectangle d’or on peut construire la spirale d’or qui ressemble à la spirale de Fibonacci.
|
|
|
|
|
|
|
La spirale d’or croissante : Soit LN = 1 et JL = \varphi tel que : \frac{JL}{LN} =\frac{\varphi }{1} = \varphi |
|
|
La spirale d’or croissante : En partant d’un rectangle d’or de longueur a+b et de largeur a, on construit un grand carré de côté la largeur a du rectangle. On réitère l’opération dans le rectangle restant qui est un rectangle d’or … et ainsi de suite, … Puis, on construit des quarts de cercle dans les carrés.
|
|
|
En partant du carré : 1°/ Tracer un carré ABCD de 8 cm de côté. Vous venez de dessiner la spirale de Fibonacci. |
|
|
Le nombre plastique, une belle analogie avec le nombre d’or. On remplace les rectangles dans la spirale de Fibonacci par des triangles équilatéraux. |
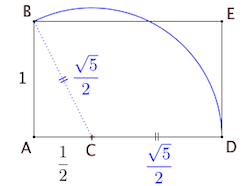
5°/ Le triangle d’or : on appelle triangle d’or un triangle isocèle dont les côtés sont dans le rapport du nombre d’or. De ce fait, les deux triangles d’or possible ont des angles à la base de 36° ou 72°. Celui d’angle de base à 36° est plutôt applé triangle d’argent.
 |
Dans le triangle ACH rectangle en H |
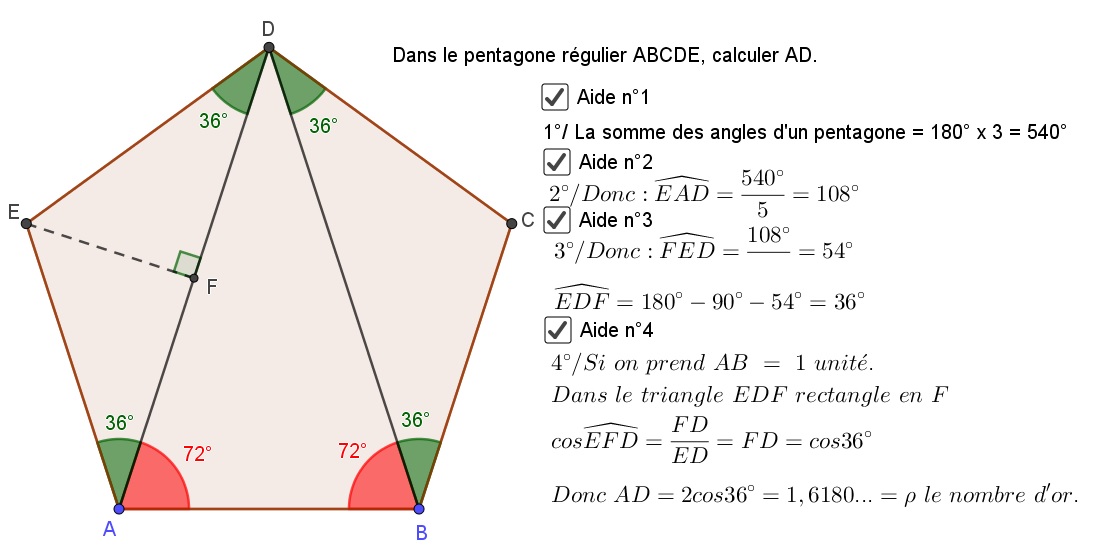 |
Il faut prendre 2 triangles d’or AEC et BCD d’angles de bases 36° et un triangles d’or ABD d’angles de bases 72°. On obtient un pentagone d’or : Si : \frac{AD}{AB}=\frac{BD}{BC}=\frac{AD}{AE}=\varphiEn fait, tous les pentagones respectent cette propriété est ce sont donc tous des pentagones d’or. |
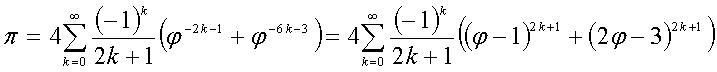 |
\pi et le nombre d’or. |
| \varphi = \sqrt{1+ \sqrt{1+\sqrt{1 + \sqrt{1+...}}}} |
Le nombre d’or et les racines continues : \varphi ^{2}= 1+ \varphi \\donc \ \varphi = \sqrt{1 + \varphi} = \sqrt{1+\sqrt{1 + \varphi}} = \sqrt{1+ \sqrt{1+\sqrt{1 + \varphi}}} |
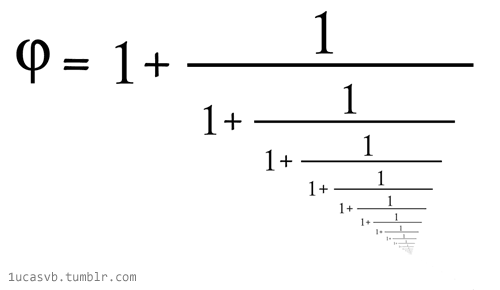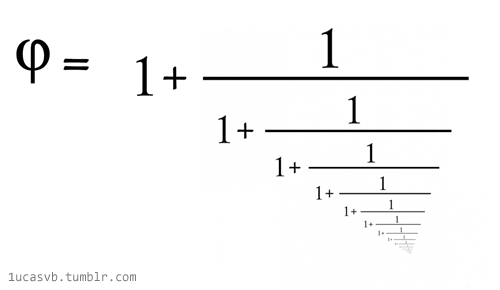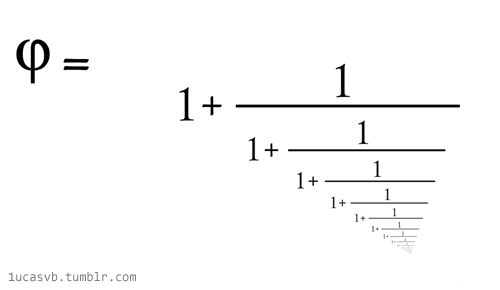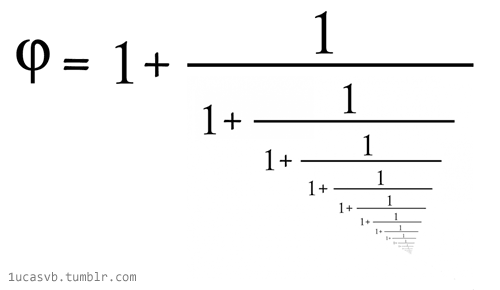 |
Le nombre d’or et les fractions continues : \varphi ^{2}= \varphi +1 \\ donc \ \varphi = 1 + \frac{1}{\varphi } = 1+ \frac{1}{1+\frac{1}{\varphi }} |
| cos \frac{\pi \ rad}{5}= cos \ 36^{\circ} = \frac{1+\sqrt{5}}{4}=\frac{\varphi }{2} | La trigonométrie d’or. |
En mathématiques, la suite de Fibonacci est une suite d’entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent, en partant de 0 et de 1 :
Cette suite célèbre est constituée en partant de 0 puis 1. On obtient les nombres suivants en additionnant les deux nombres précédents.
0 ; 1 ; 1 = 0 + 1 ; 2 = 1 + 1; 3 = 2 + 1 ; 5 = 3 + 2 ….
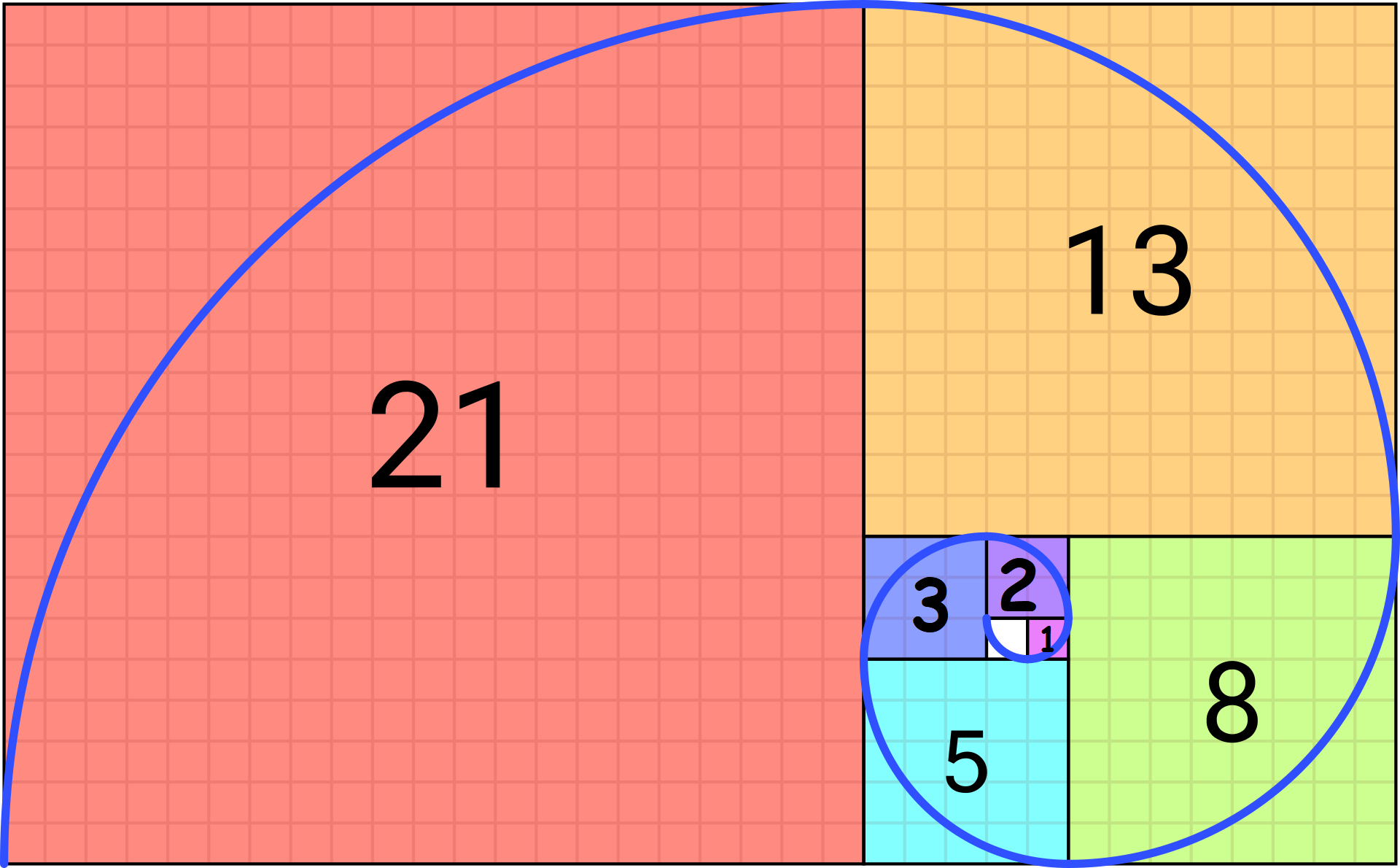 |
En partant d’un carré de côté 1, on juxtapose un autre carré de côté 2, ce qui crée un rectangle de longueur 1+2 = 3 et de largeur 1+1 = 2. Puis on juxtapose un autre carré de côté 3, ce qui crée un rectangle de longueur 2+5 = 5 et de largeur 1+2 = 3. Et ainsi de suite. Chaque carré présente des côtés qui suivent la suite de Fibonacci. Le lien avec le nombre d’or passe d’abord par la ressemblance avec le rectangle d’or, puis par le fait que le rapport de 2 nombres consécutifs de la suite se rapproche de plus en plus de \varphi .
|
|||||||||||||||||||||||||||||||||||
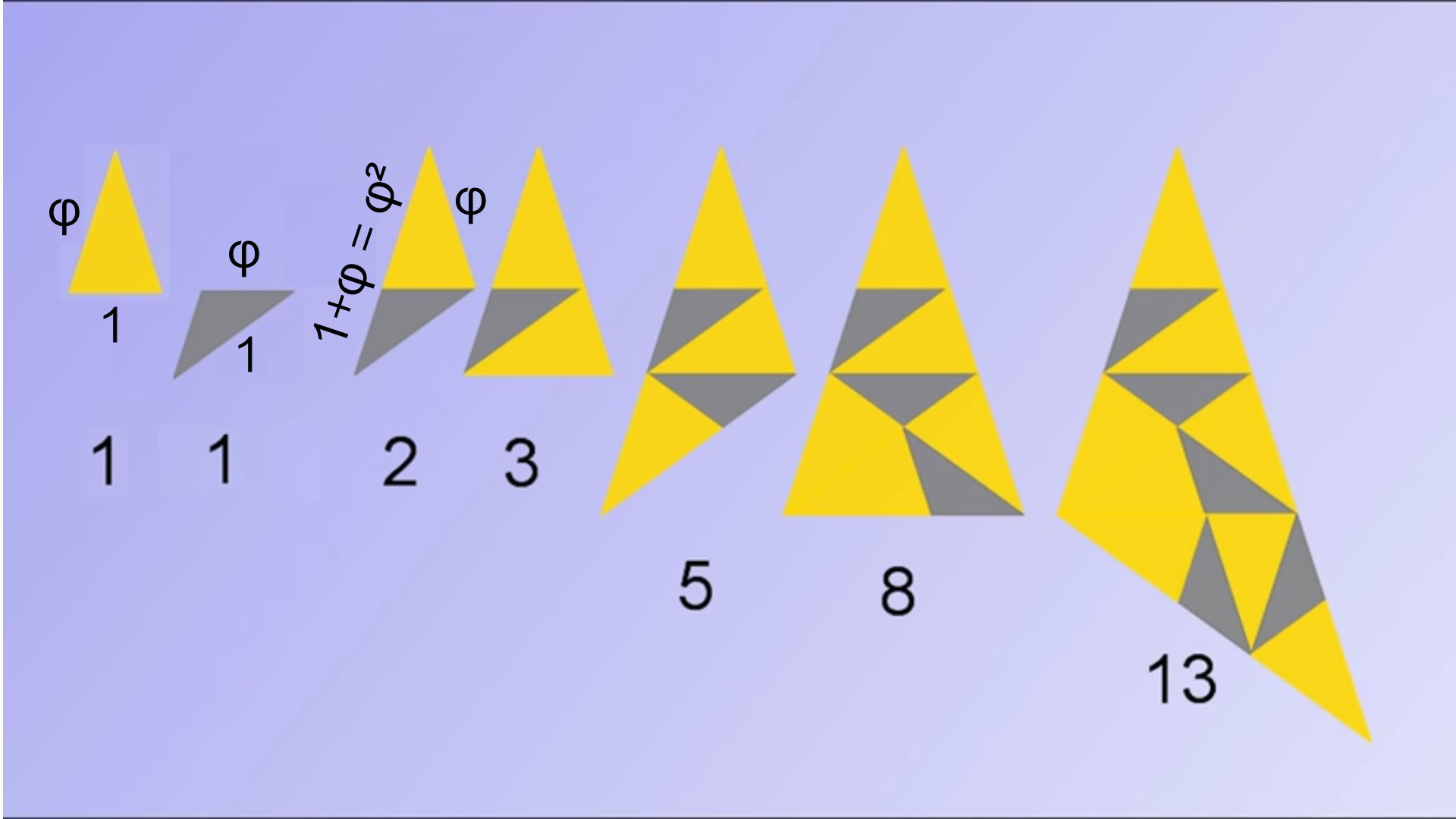 |
Mais on peut aussi retrouver cette suite en assemblant des triangles d’or et d’argent : Et bien sur, si on divise le nombre de triangle d’or par le nombre de triangle d’argent de chaque triangle on se rapproche de de plus en plus de \varphi .
|
Mais comment trouver le nième terme de la suite de Fibonacci sans avoir à calculer les précédents ?
|
La formule de Binet permet de déterminer le nième terme Un de la suite de Fibonacci : \Huge{ U_{n}=\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{n}-\left ( \frac{1-\sqrt{5}}{2} \right )^{n} }{\sqrt{5}}} Ce qui est extraordinaire avec cette formule, c’est l’on obtient des nombres de Fibonacci, qui sont des nombres entiers, en utilisant le nombre d’or, qui a un développement infini. Le nombre d’or, (1 + √5)/2, est approximativement égal à 1,618033… Le nombre √5 vaut, quant à lui, environ 2,236068… Et pourtant, en faisant le calcul, la virgule disparaît : toutes leurs décimales « s’emboîtent » impeccablement pour donner un nombre entier. Par exemple, si l’on cherche le dixième nombre de Fibonacci, on peut le calculer ainsi :
|
Le nombre d’or est certainement le seul nombre pour lequel on peut faire coïncider une progression géométrique (on passe d’un nombre à son suivant en multipliant par un même nombre, ici \varphi ) et une somme, en l’occurrence la somme des 2 termes précédents. Rappel : \varphi ^{2} = 1+\varphi
| Suite Géométrique | \varphi ^{0} = \color{red}1 | \varphi ^{1} = \color{red}\varphi | \varphi ^{2} = \color{red}1+\varphi | \varphi ^{3}=\varphi \times \varphi^{2} =\varphi \times (1+\varphi )=\varphi +\varphi^{2} = \varphi +1+\varphi = \color{red}1 + 2\varphi | \varphi ^{4}=\varphi \times \varphi^{3} =\varphi \times (1+2\varphi )=\varphi +2\varphi^{2} = \varphi +2+2\varphi =\color{red} 2 + 3\varphi | \varphi ^{5}=\varphi \times \varphi^{4} =\varphi \times (2+3\varphi )=2\varphi +3\varphi^{2} = 2\varphi +3+3\varphi =\color{red} 3 + 5\varphi | \varphi ^{n}=\color{red}\varphi ^{n-1}+\varphi ^{n-2} |
| Somme des 2 termes précédents | 1 =\varphi ^{0} | \varphi ^{0}+\varphi ^{1}=1+ \varphi | \varphi ^{1}+\varphi ^{2}=\varphi+1+\varphi = 1+2\varphi | \varphi ^{2}+\varphi ^{3}=1+\varphi+1 + 2\varphi = 2 + 3\varphi | \varphi ^{3}+\varphi ^{4}=1 + 2\varphi + 2 + 3\varphi =3 + 5\varphi | \varphi ^{n-1}+\varphi ^{n-2} | |
| Suite d’inverses | 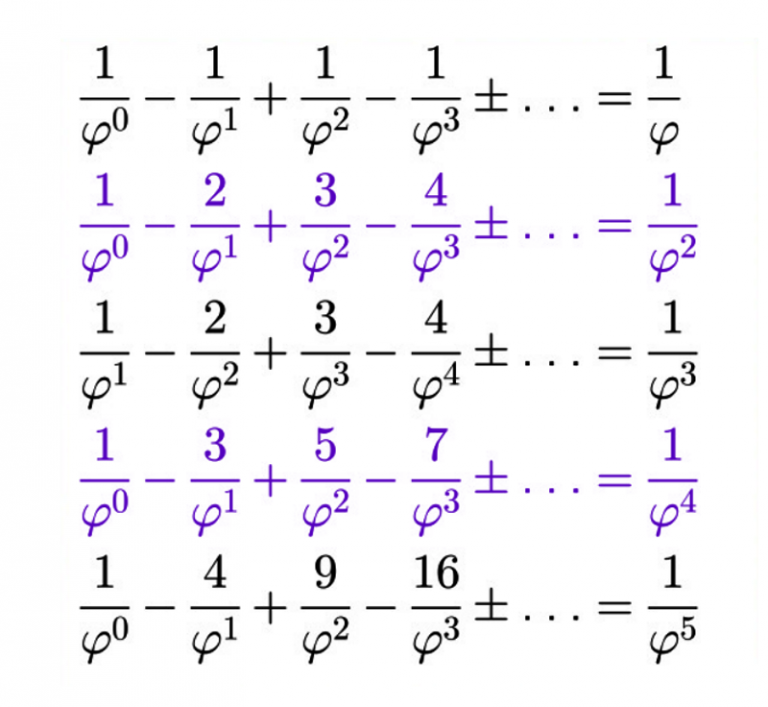 |
||||||
| L’échelle d’or | 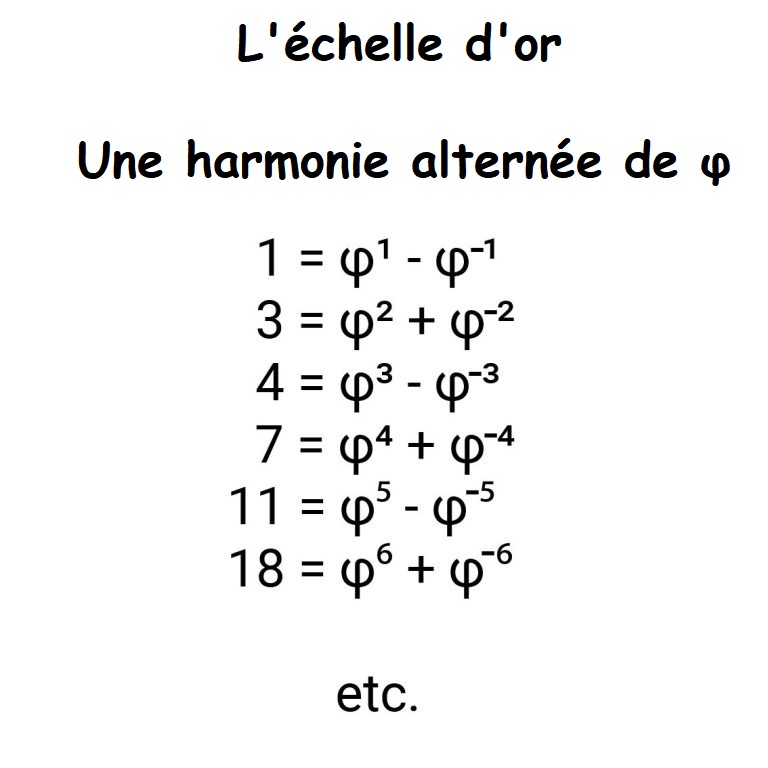 |
||||||
10°/ Le nombre d’or est partout :
On peut retrouver le nombre d’or un peu partout, soit du fait d’une intention humaine, soit pour des raisons logiques :
|
Le Corbusier (1887-1965) : architecte qui à développé toute une théorie autour de l’harmonie du nombre d’or. Il invente en 1945 le Modulor qui sera son modèle étalon pour la construction des habitations et qui remplace le mètre. Plus adapté que le système métrique, car il est directement lié à la morphologie humaine. |
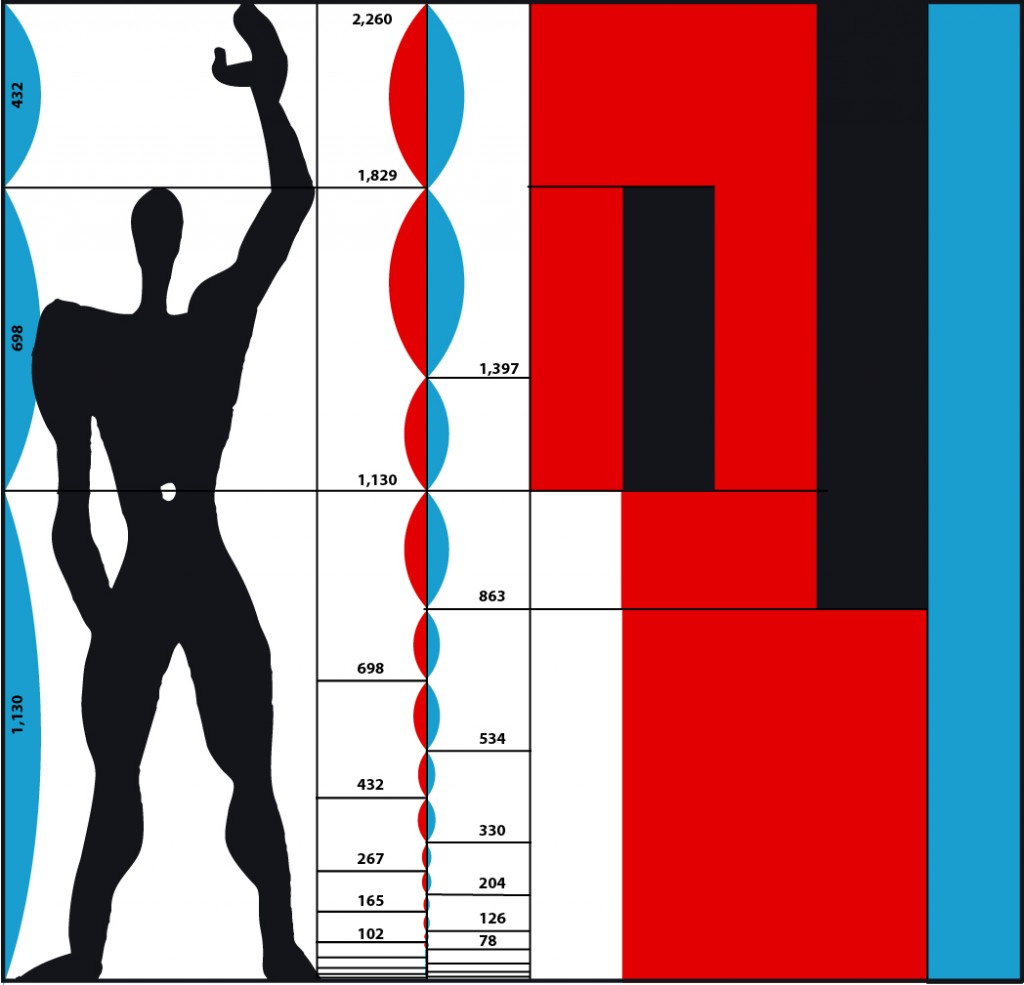 |
|
La phyllotaxie : pour ne pas ce faire de l’ombre les feuilles d’une branche se décalle d’un angle de 137,5°. En effet : 137,5° + 137,5° \varphi = 360°. |
 |
| Les pétales de fleurs : Rares sont les fleurs qui ne comptent pas 5, 8 ou 21 pétales. Il s’agit des nombres de la suite de Fibonacci intimement liée au nombre d’or. |
|
| Des constructions humaines : les rapports longueur sur largeur de la carte de crédit (taille standard CR80 : 85,6 cm sur 54 cm), longueur d’un violon sur son corps ou encore hauteur d’un vélo sur hauteur de sa roue. |  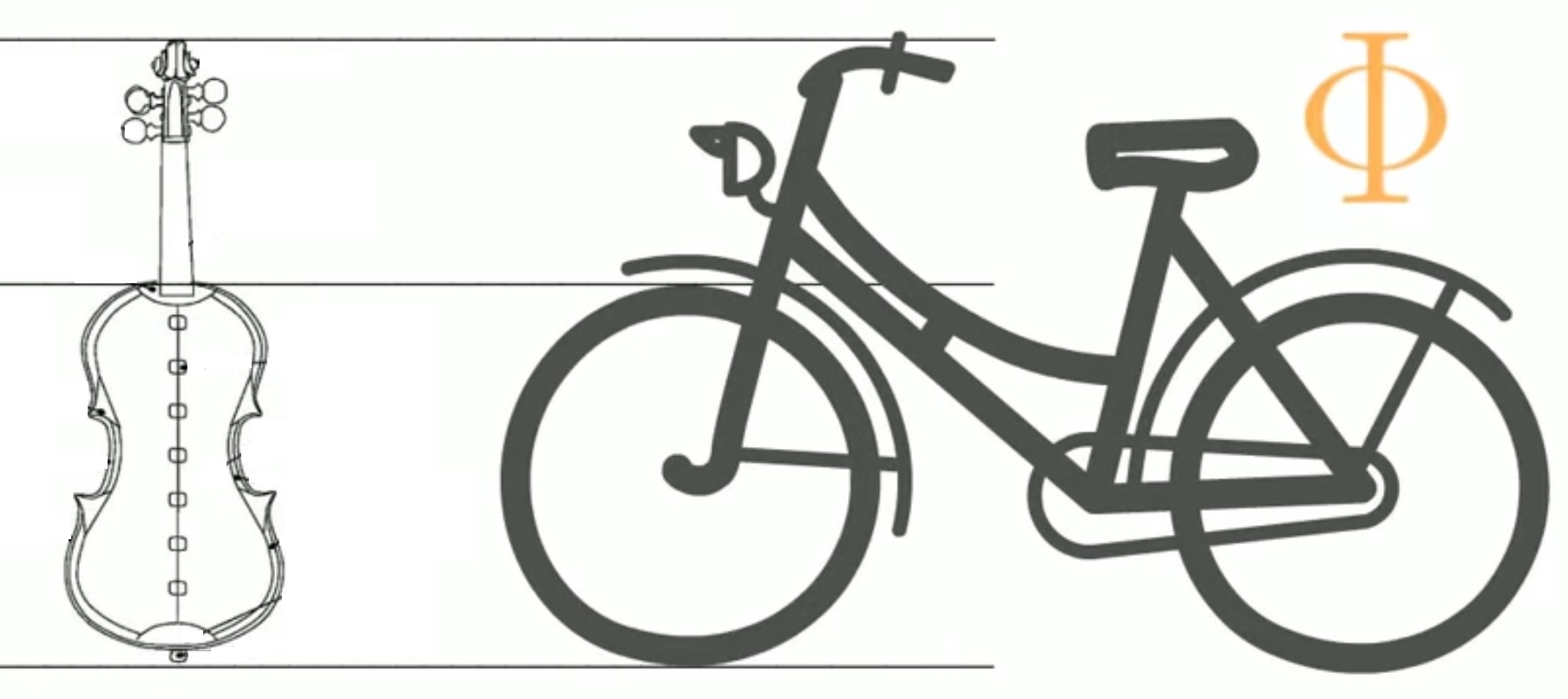  |
|
Pyramide du Louvre : construite sur l’esplanade du Louvre à Paris, par l’architecte Ieoh Ming Pei, elle respecte la proportion du nombre d’or si on mesure sa largeur, sa hauteur et ses arêtes. Si pour la pyramide de Kéops on peut avoir des doutes quand à savoir si les constructeurs on sciemment utilisés le nombre d’or, ce n’est pas le cas ici.
|
 |
| Les logos : les entreprises ont bien comprit le côté subjectif du nombre d’or et elles le font apparaître partout dans leurs logos. |    |
| L’art : les peintres recherche l’harmonie et les belles proportions. C’est donc tout naturellement que l’on retrouve la divine proportion dans leurs œuvres. |   |
Il y a des cas contestables, car ce n’est pas parce que le rapport de 2 nombres donne 1,618 que le nombre d’or y est pour quelque chose. Par exemple je mesure 1,89 m pour 55 kg (oui je ne suis pas bien épais …), et bien \frac{89}{55} =1,61818.... \approx \varphi .
|
Les proportions humaines : la taille d’un homme divisée par la distance du sol au nombril est égal au nombre d’or. La largeur de la bouche divisée par la largeur du nez aussi. |
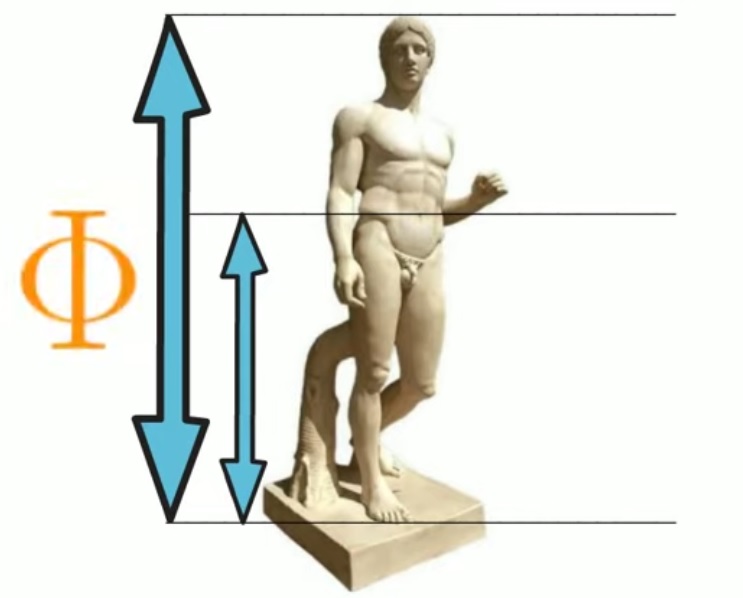 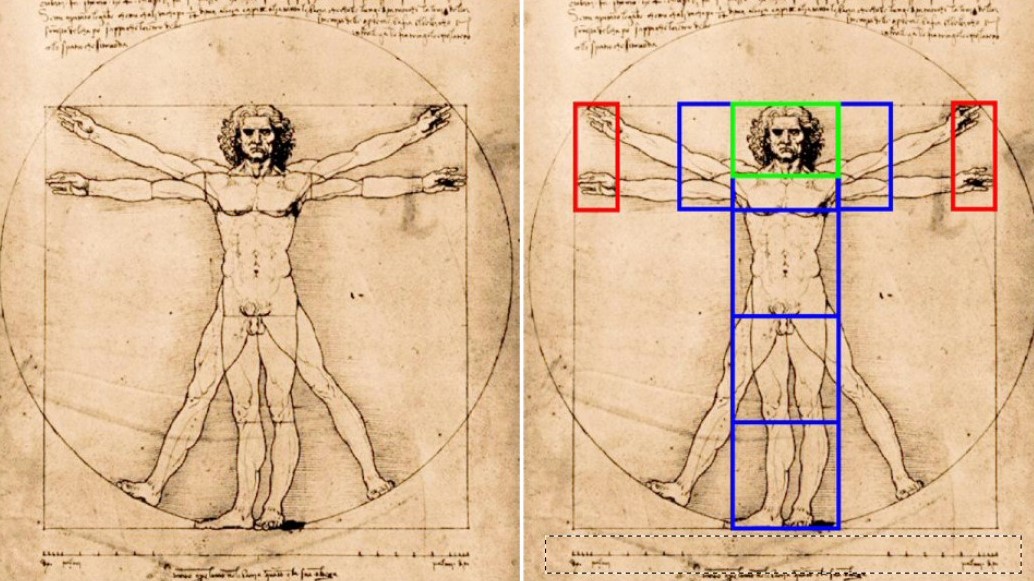 |
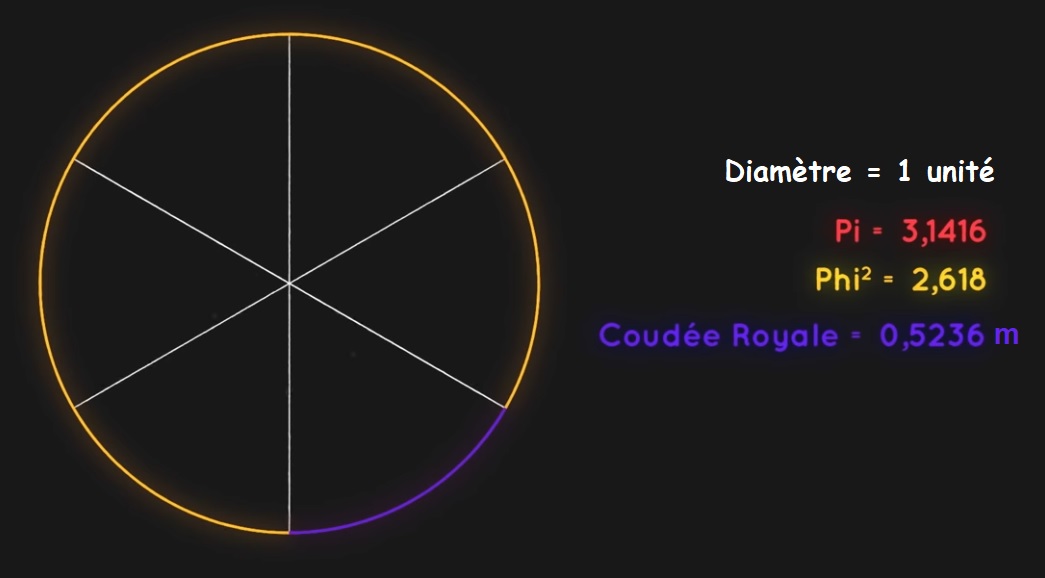
| La coudée royale : mesure de référence des architectes égyptiens qui est la longueur du bout du majeur du Pharaon jusqu’à son coude c’est à dire 52,36 cm. Hasard ou coïncidence, si on prend un cercle de 1 unité de diamètre alors son périmètre fera \pi . La coudée royale sera le sixième de ce périmètre : \frac{\pi }{6} \approx 0,523598... \ unités Il reste \frac{5\pi }{6} \approx 2,61799...\approx \varphi ^{2} \ unités |
|
| Le Parthénon : Temple, dédié à la déesse Athéna en 447 av JC, situé sur l’Acropole d’Athènes en Grèce. On peut repérer une multitude de rectangle d’or. Est-ce voulu, ou est-ce simplement parce que la dimension de ce rectangle est très agréable à l’œil ? |
 |
|
La pyramide de Kéops : en triturant toutes les mesures de la pyramide, on peut retrouver le nombre d’or dans de nombreux rapport. De là à affirmer que c’était voulu par les bâtisseurs … |
 |
|
Astronomie : si l’on divise le nombre de jours (terrestres) que la Terre met pour faire sa révolution (sidérale) autour du soleil, par le nombre de jours (terrestres) que Vénus met pour faire sa révolution (sidérale), on obtient comme résultat : le nombre d’or φ (à 99.53%). La voie lactée a une forme en spirale, peut être celle de Fibonacci. |
 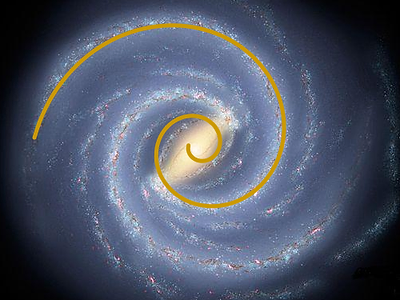 |
| L’ADN : C’est le Dr ingénieur en mathématique et informatique Jean-Claude Perez qui a découvert la présences du ratio doré sous forme de la suite de fibonacci dans la répartition des bases de notre ADN ! Le rapport de la longueur d’une hélice sur sa largeur est égale au nombre d’or. Vue de dessus, il y a 10 barreaux par pas de l’hélice d’ADN : si qui donne un triangle d’or d’angle 36°. |
 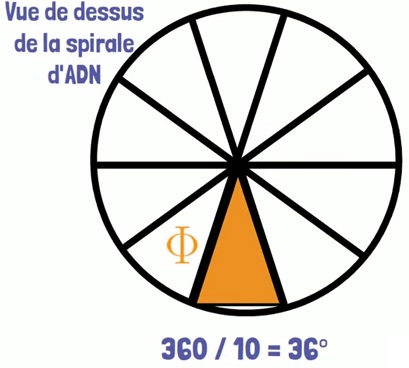 |
| La nature : en cherchant bien on peut trouver la divine proportion un peu partout dans la nature. Cela semble normal, puisque nous sommes sensible à cette proportion c’est quelle est soit très présente, soit quelle est utile voire parfaite. |    |
|
La bible : la recherche est un peu tirée par les cheveux. Dans l’Apocalypse selon Saint Jean. Chapitre 21 verset 17 : Il en mesura aussi la muraille, de cent quarante-quatre coudées, mesure d’homme, qui est aussi mesure d’ange. Sin(666°) = cos(144°) = \frac{-\varphi }{2} 666 étant le nombre de la bête Rem : 666 = 234 + 432 = 13 x 18 + 3 x 144 234 et 432 sont des nombres miroir, Chapitre 13 verset 18 et 144 la longueur de la muraille. |
 |
|
Le drapeau de l’indépendance du Chili vis-à-vis de l’Espagne signée en 1818. Il est conservé au Musée d’Histoire Nationale de Santiago.. Le drapeau a toujours été conservé dans des musées, sauf pendant une vingtaine d’années. En effet, au début des années 80, il a été « kidnappé » par un commando en signe de protestation contre la dictature d’Augusto Pinochet. C’est ainsi qu’en 1912 on a choisi de simplifier le modèle. À titre de comparaison, vous pouvez voir en bas le design du drapeau de 1818 (à gauche) et celui du drapeau actuel (à droite). Dans ce dernier, la région bleue n’est qu’un carré sur lequel est centrée une étoile dont le diamètre du cercle circonscrit est la moitié du côté du carré. On aboutit de cette façon à un modèle de rapport longueur / largeur égal à 3:2 (comme celui du drapeau français).
|
|
|
On peut réaliser de très beaux dessins avec le nombre d’or. Le nombre d’or est mis en œuvre en cercles, servant de rapport mathématique pour générer des designs esthétiquement agréables. Compte tenu de sa prévalence dans la nature, l’apparence naturelle des résultats n’est pas surprenante. Le Diamant d’Or présente une dissection monomorphe asymptotique du triangle équilatéral. Chaque carreau suit des proportions alignées sur le nombre d’or par rapport au triangle extérieur. Spirale dorée créée à l’aide de triangles équilatéraux. La spirale de Padovan suit une séquence récursive semblable à la séquence de Fibonacci. |
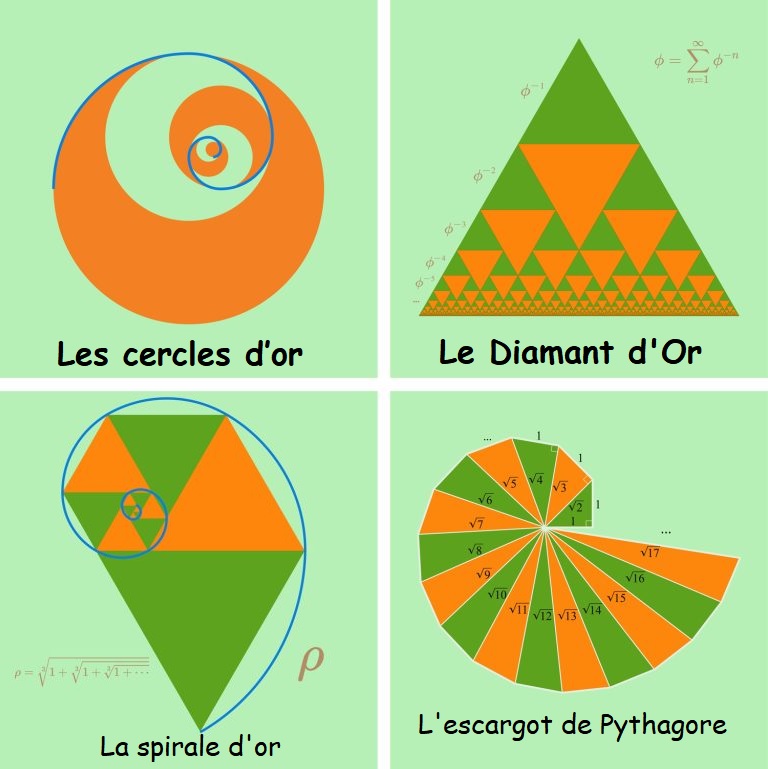 |
|
La philosophie du Yin Yang est représentée par le « symbole taichi » ( taijitu ). En fait, le Yin Yang est un concept de dualisme , décrivant comment des forces apparemment opposées ou contraires peuvent en réalité être complémentaires, Curieusement, dans le symbole du taichi sont cachés le nombre d’or et son inverse. |
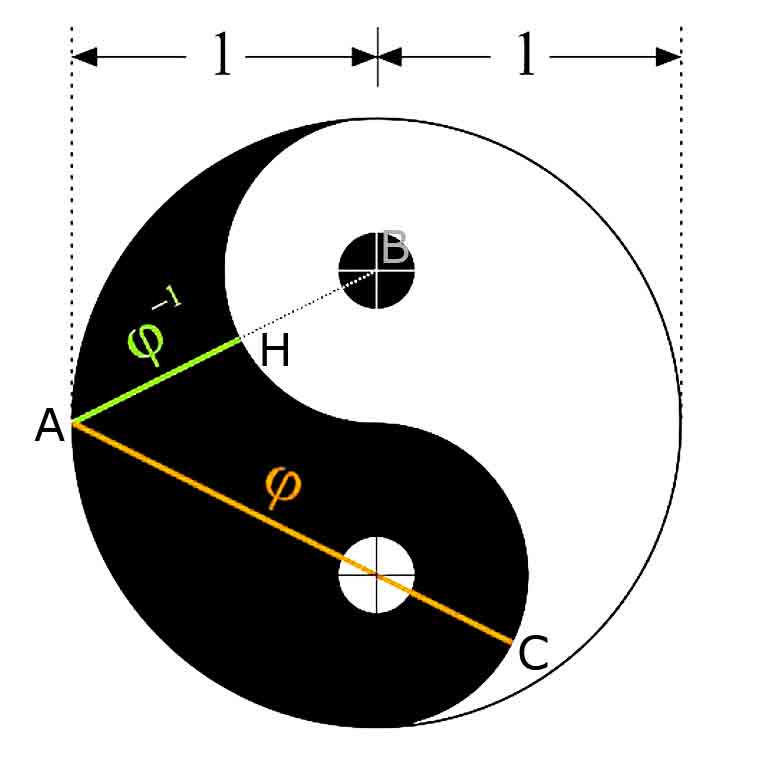 |
Le nombre d’or fait partie d’une vaste famille appelée « rapports métalliques » ou « Ratio métalliques ». Ces rapports décrivent une relation récursive entre les côtés d’un rectangle.
Étant donné un rectangle de côtés de longueurs A et B ( avec B > A ), les rapports métalliques satisfont l’équation :
|
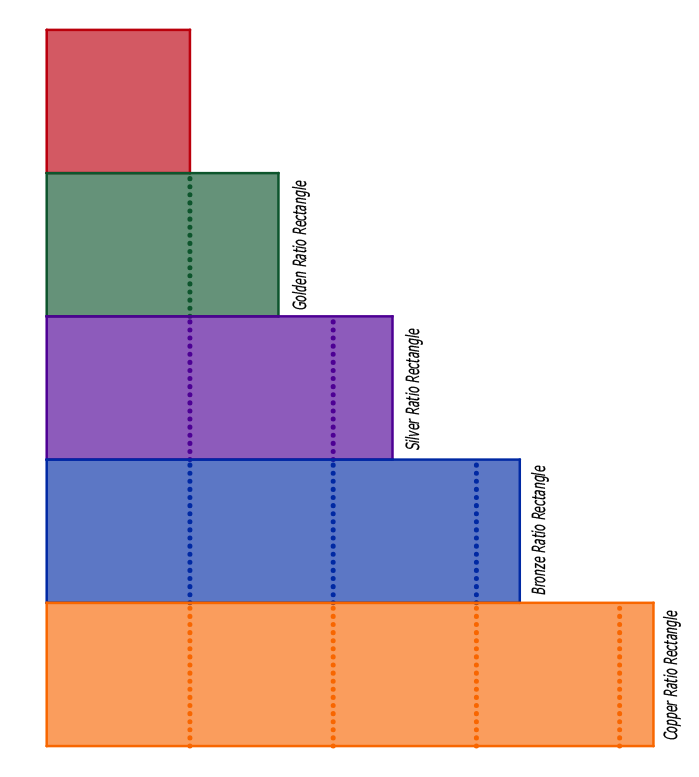 |
N°/ La somme d’une suite géométrique infinie est finie :
Comment la somme infinie d’une suite de nombre plus petit que un, peut-elle donner un nombre fini ?
Pour \ q < 1 : \large{ q^{0}+q^{1}+q^{2}+q^{3}...=1+q+q^{2}+q^{3}+...=\frac{1}{1-q}} \\ \normalsize{Pour \ q =} \Large{\frac{1}{2} : (\frac{1}{2})^{0}+(\frac{1}{2})^{1}+(\frac{1}{2})^{2}+(\frac{1}{2})^{3}...=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}...=\frac{1}{1-\frac{1}{2}}=2} \\ \normalsize{ Pour \ q=} \Large{ \frac{1}{3} : (\frac{1}{3})^{0}+(\frac{1}{3})^{1}+(\frac{1}{3})^{2}+(\frac{1}{3})^{3}...=1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}...=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}} \\ \normalsize{ Pour \ q=} \Large{ \frac{1}{4} : (\frac{1}{4})^{0}+(\frac{1}{4})^{1}+(\frac{1}{4})^{2}+(\frac{1}{4})^{3}...=1+\frac{1}{4}+\frac{1}{16}+\frac{1}{64}...=\frac{1}{1-\frac{1}{4}}=\frac{4}{3}}|
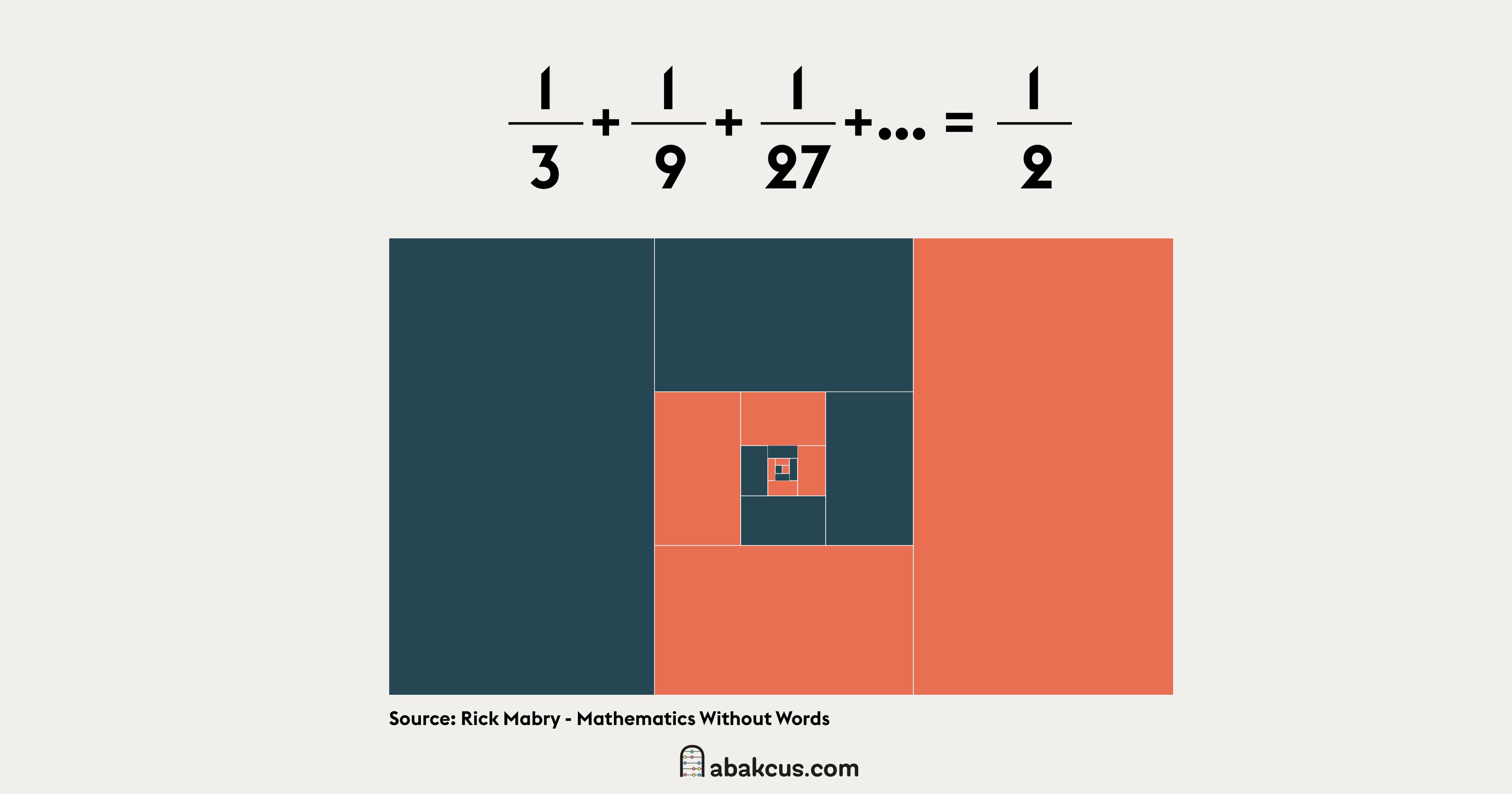
\LARGE{\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+...=\frac{1}{2}}
Démonstration visuelle : si on ajoute le tiers de chaque partie on obtiendra la moitié du rectangle de départ.
|
O°/ Le nombre un : Pourquoi faire simple quand on peu faire compliqué.
Voici plusieurs façon d’écrire le nombre un.
| (sin x)² + (cos x)² = 1 | La fameuse équation de trigonométrie. |
 |
Vous pouvez écrire le nombre 1 comme une somme de 48 fractions différentes, où chaque numérateur est 1 et chaque dénominateur est un produit d’exactement deux nombres premiers. |
|
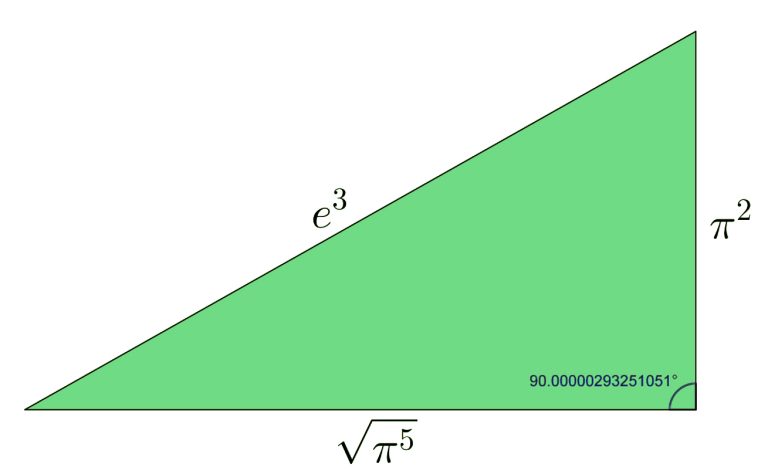
\Huge \frac{\pi^{4}+\pi^{5}}{e^{6}}\approx 1
|
Cela signifie que ce triangle est presque un triangle rectangle.
|
P°/ Le nombre e :
Le nombre e est la base des logarithmes naturels, c’est-à-dire le nombre défini par ln ( e ) = 1 {\displaystyle \ln(\mathrm {e} )=1}. Cette constante mathématique, également appelée nombre d’Euler ou constante de Néper en référence aux mathématiciens Leonhard Euler et John Napier[b], vaut environ 2,71828.
La décomposition de cette fonction en série entière mène à la définition de e par Euler comme somme de la série :
Ce nombre apparaît aussi comme limite de la suite numérique de terme général ( 1 + 1 n ) n et dans de nombreuses formules en analyse telles que l’identité d’Euler e i π = − 1 ou la formule de Stirling qui donne un équivalent de la factorielle. Il intervient aussi en théorie des probabilités ou en combinatoire.
Euler démontre en 1737 que e est irrationnel, donc que son développement décimal n’est pas périodique, et en donne une première approximation avec 23 décimales. Il explicite pour cela son développement en fraction continue. En 1873, Charles Hermite montre que le nombre e est même transcendant, c’est-à-dire qu’il n’est racine d’aucun polynôme non nul à coefficients entiers.
Mais le plus improbable, c’est que l’on retrouve cette constante e dans la croissance continue.
Si le prix d’un tonneau de blé à 100 euros augmente de 50 %, il se retrouve à 150 euros ; et s’il augmente à nouveau de 50 %, le voilà à 225 euros. La deuxième augmentation (+ 75 euros) est plus élevée que la première (+ 50 euros) car elle s’applique au prix ayant déjà été augmenté. Bref, deux augmentations de 50 % font une augmentation de 125 %. Autrement dit, le prix final n’a pas été multiplié par 2, mais par 2,25.
Continuons d’affiner notre processus :
Imaginez maintenant que le prix du tonneau de blé augmente de 10 % tous les dixièmes de mois, c’est-à-dire en gros tous les trois jours. Cela signifie qu’à la fin du mois il aura subi dix augmentations d’un dixième, c’est-à-dire dix multiplications successives par 1,1. Au total, il aura donc été multiplié par 1,110 qui est approximativement égal à 2,59.
Si maintenant cette quantité avait subi 100 augmentations d’un centième, elle serait multipliée par 1,01100 qui vaut environ 2,705 à la fin du mois.
Et si nous précisons encore, 1 000 augmentations d’un millième auraient produit une multiplication par 2,717. Ces informations sont condensées dans le tableau suivant.
| Nombre d’étapes | Prix final | Facteur d’augmentation |
| 2 | 100 x 1,5 x 1,5 = 225 = 100 x 2,5 | 2,5 |
| 10 | 100 x 1,1010 = 259,374246 | 2,59374246 |
| 100 | 100 x 1,01100 = 270,4813829 | 2,704813829 |
| 1 000 | 100 x 1,0011 000 = 271,6923932 | 2,716923932 |
| 10 000 | 100 x 1,000110 000 = 271,8145927 | 2,718145927 |
| n |
100\times\left(\frac{100+n}{100}\right)^{n}
|
\approx 2,71828 = e
|
Autrement dit, lorsqu’une somme augmente n fois de n%, cela revient a multiplier cette somme par la constante e.
Lorsqu’elle présenta son introduction en Bourse, la société Google, folie des grandeurs oblige, décida symboliquement de lever 2 718 281 828 dollars, soit e milliards de dollars, arrondi à l’unité.