A°/ Le calcul de Saint-Exupéry :
B°/ La multiplication des baisers :
C°/ Des grains de riz sur un échiquier :
D°/ La propagation des rumeurs :
E°/ Calcul d’intérêts :
F°/ Les très grands nombres :
G°/ Des puissances bien ordonnées :
H°/ 1k + 2k + 3k+ … +nk et les nombres de Bernoulli mais aussi le tout premier programme informatique :
I°/ Les Cent mille milliards de poèmes :
J°/ Ordre de grandeur :
K°/ Le nom des puissances :
L°/ Les épidémies :
M°/ Notation ancienne :
A°/ Le calcul de Saint-Exupéry :
|
Voici un extrait du petit prince de Saint-Exupéry (1951). Les hommes occupent très peu de place sur la terre. Si les deux milliards d’habitants qui peuplent la terre se tenaient debout et un peu serrés, comme pour un meeting, ils logeraient aisément sur une place publique de vingt milles de long sur vingt milles de large. On pourrait entasser l’humanité sur le moindre petit îlot du pacifique. Les grandes personnes, bien sûr, ne vous croiront pas. Elles s’imaginent tenir beaucoup de place. Elles se voient importantes comme des baobabs. Vous leur conseillerez que donc de faire le calcul. Elles adorent les chiffres : ça leur plaira. Mais ne perdez pas de temps à ce pensum. C’est inutile. Vous avez confiance en moi. |
 |
Les mathématiciens aiment bien Saint-Exupéry, mais le résultat d’un calcul n’est pas une question de confiance, tout le monde peut se tromper. Vérifions le calcul de Saint-Exupéry, sachant que le mille romain vaut 1 482 m ( le mille Anglo-Saxons valant 1 609,3 m) :
Considérons que l’on peut faire tenir quatre hommes sur un mètre carré.
| Largeur
du carré L |
1 m | 10 m | 1 mille
=1 482 m |
20 milles = 29 640 m | 22 360.67 m
= 15 milles |
43,9 km |
| Surface | 1 m² | 100 m² | 1 mille² =
2 196 324 m² |
400 milles² = 878 529 600 m² = 878,5296 km² |
\frac{7,7\times 10^{9}}{4}
= 1,925 x 109 m²= 1 925 km² |
|
| Personnes P | 4 hommes | 400 hommes | 8 785 296 hommes | 3 514 118 400 hommes | 2 milliards hommes | 7,7 milliards hommes en 2021 |
A titre de comparaison, le Territoire de Belfort a une superficie de 609 km², les PO de 4 116 km², les Pyrénées-Atlantiques de 7712 km² et la Corse de 8722 km².
Si on préfère 1 personne par m², cela fera 7,7 x 109 m² = 7 700 km²
Formule générale pour avoir la largeur du carré : L =
Reprenons la question précédente, mais en parlant de volume cette fois.
Considérons qu’un individu peut se glisser dans un parallélépipède rectangle de volume :
1,70 m × 0,40 m × 0,15 m soit 0,102 m3,
Donc dans un mètre cube on peut caser 10,2 hommes, c’est à dire pratiquement dix hommes (ou dix femmes).
Dans un cube de un kilomètre de côté, on pourrait donc caser, serrés comme des sardines en boîte, 10 milliards d’êtres humains.
1 km × 1km × 1km = 1 km3 = 1000 m × 1000 m × 1000 m = 109 m3
B°/ La multiplication des baisers :
Un baiser abrège la vie humaine de 3 minutes, affirme le Département de Psychologie du Western State College, Gunnison (Colorado). En effet, le baiser provoque de telles palpitations, que le cœur travaille en 4 secondes plus qu’en 3 minutes. Les statistiques prouvent que 480 baisers raccourcissent la vie d’un jour, que 3 360 baisers vous privent d’une semaine et que 175 320 baisers, c’est tout simplement une année de perdue.
Poème de Paul Morand ( USA 1927 )
24 h = 24 × 60 min = 1 440 min → 1440 / 3 = 480 baisers
1 semaine = 7 j → 480 × 7 = 3 360 baisers
1 année = 365,25 jours → 480 × 365,25 = 175 320 baisers
C°/ Des grains de riz sur un échiquier :
|
Il était une fois en Inde, un roi nommé Belkib (ou Bathait) qui s’ennuiait à la cour. Il demande qu’on lui invente un jeu pour le distraire. Le sage Sissa invente alors le Chaturanga, l’ancêtre du jeu d’échecs, ce qui ravit le roi. Pour le récompenser il lui demande : « Comment veux-tu être récompensé ? » |
 |
Imprudente promesse ! Le savant mathématicien attaché à la Cour eut tôt fait de démontrer à l’empereur que jamais la terre ne pourrait produire assez de riz pour qu’il tienne son engagement.
Le calcul du nombre de grains de riz sur la dernière case de l’échiquier est assez facile à obtenir en utilisant les puissances.
Il y a donc environ 263 = 9 × 1018 grains de riz sur la dernière case de l’échiquier, soit un nombre écrit avec un 9 suivis de 18 zéros : C’est-à-dire 9 milliards de milliards de grains de riz.
En 1997 la production mondiale de riz était de 573,2 millions de tonnes.
Sachant qu’un grain de riz pèse à peu près 10 mg ( cad 10-5 kg), les 9 milliards de milliards de grains de riz représentent :
9,2 × 1018 × 10-5 = 9,2 × 1013 kg = 9,2 × 1010 tonnes cad 92 milliards de tonnes, ce qui représente 160 fois la production de 1997 !!!
D°/ La propagation des rumeurs :
Dans un petit village du sud de la France, le premier jour de l’année, trois personnes découvrent un terrible secret. Ne pouvant garder ce secret pour eux seul, le lendemain chacune des trois personnes le dévoilent à trois autres. Le lendemain les 9 personnes qui connaissent maintenant ce terrible secret, l’annoncent elles aussi à trois autres personnes, et ainsi de suite les jours suivants.
La question est de savoir au bout de combien de temps les 500 personnes du village seront au courant ou alors de savoir combien de personnes connaîtront le secret au bout d’un mois de 31 jours.
Le nombre de personne P connaissant le secret, en fonction du nombre de jour J, est donné par la formule :
P = 3J→ Ln P = J × Ln 3 → J =
P = 500 personnes → J = = 5,657 jours
J = 31 jours → P = 331 = 6,18 × 1014 personnes = 617 673 milliards de personnes
Pour que les 6 milliards d’êtres humains de la terre entière soient prévenus, il faudra :
P = 6 × 109 personnes → 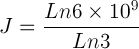
E°/ Calcul d’intérêts :
Le calcul des intérêts peut donner le vertige suivant la méthode utilisée pour gérer ses intérêts. Deux solutions s’offrent à nous, soit l’on récupère chaque année les intérêts produits par le capital placé, soit on les laisse et les intérêts qui s’ajoutent donc au capital de départ et génèrent eux aussi leurs propres intérêts.
Soit P le placement de départ, à un intérêt I % par an, et durant une période A années. Soit S la somme finale obtenue ( capital et intérêts ).

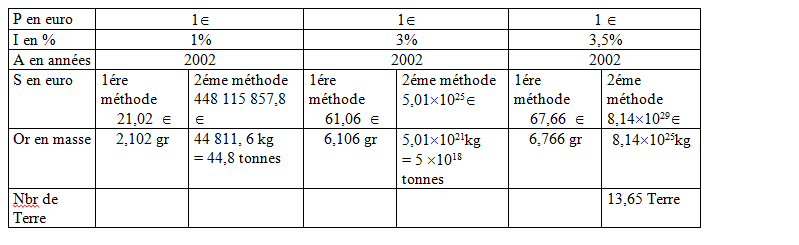
1 kg d’or vaut 10 000 € et la terre a une masse de 5,96 × 1024 kg
Notons que si la mise de départ avait été de 10 euro, toutes les sommes finales seraient multipliées par 10, et pour un intérêt I de 3,5% sur 2002 ans, on arriverait à une masse d’or égale à 136,5 fois la Terre.
Voici un Géogébra qui permet de faire différent calculs :
F°/ Les très grands nombres :
Dans les années 40, Edward Kasner (USA) publie un livre « Mathematics and the Imagination » dans lequel apparaît le mot Googol (Gogol en Français). Ce mot ne serait pas inventé par Kasner mais il l’aurait repris de son neveu âgé à l’époque de 9 ans.
Il serait impossible, dans le système décimal, d’écrire ce nombre sur du papier car il contient plus de chiffres qu’il y a d’atomes dans l’univers visible que l’on évalue à 1082.
L’inverse du gogolplex, nombre positif extrêmement petit, est appelé gogolminex. C’est ce nombre Googol qui est à l’origine du nom du moteur de recherche Google.
Le Gogol est un 1 suivi de 100 zéros. Mais existe aussi le Gogolplex qui est un 1 suivi de Gogol zéros.
Gogol = 10100
Gogolplex = =
=
.
Mais bien sur ce n’est pas suffisant. En 1976, un mathématicien américain, Donald Knuth, a inventé une autre forme de calcul pour pouvoir écrire de plus grand nombre : la notation des puissances itérées de Knuth.
Addition : 2 + 3 = 5
Additions répétitives → multiplication : 5 + 5 + 5 = 5 x 3 = 15
Multiplications répétitives → Puissances : 5 x 5 x 5 x 5 x 5 = 55 = 3 125
Puissances répétitives → Puissances itérées de Knuth : 5 ↑ 5 = 55 = 3 125
. 5 ↑↑ 5 = 5 ↑ 5 ↑ 5 = 5^{5^{5}} = 53125 ce nombre est déjà incalculable pour une machine à calculer normale.
. 5 ↑↑↑ 5 = 5 ↑↑ 5 ↑↑ 5 etc….
Allez, comme c’est rigolo on continue. Le plus grand nombre utilisé dans une démonstration s’appelle le nombre de Graham. Le voici :
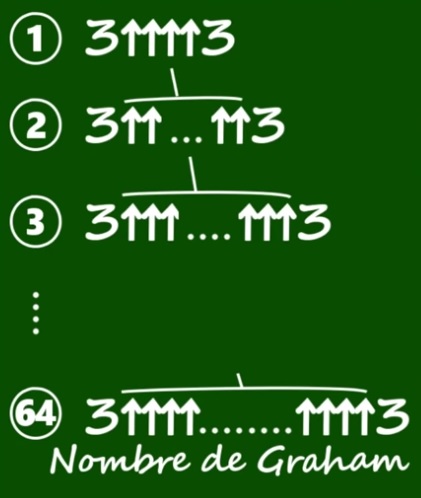 |
A chaque ligne il y a autant de flèche que le nombre précédent.
Le nombre de Graham sera celui de la 64ième ligne. |
Petite question : le Gogol est-il plus grand que la factorielle de 100.
Gogol = 10^{100}=10^{2 \times 50}=(10^{2})^{50}=100^{50} \ cad \ 50 \ facteurs \ 100 \\100! = \textcolor{red}{100} \times \textcolor{blue}{99}\times \textcolor{magenta}{98} \times ... \times \textcolor{magenta}{3} \times \textcolor{blue}{2}\times \textcolor{red}{1} \\ \ \ \ \ \ \ = (\textcolor{red}{100 \times 1}) \times (\textcolor{blue}{99\times 2}) \times ... \times (48 \times 49) \times (\textcolor{magenta}{51 \times 50})Les 50 facteurs de 100! sont supérieurs ou égaux à 100, donc :
100! > Gogol
Il existe des nombres particuliers : le nombre de Shannon (10120), c’est à dire, le nombre théorique possible de parties d’échec ou l’asaṃkhyeya (10140).
Voir ma page sur l’infini.
Bien entendu, on peut se demander ce que l’on pourrait bien compter avec de si grand nombre dans la vie de tous les jours ? Et bien, pourquoi pas de l’argent. Allez voir cette page très instructive.
G°/ Des puissances bien ordonnées :
Voici un classement un peu particulier des puissances de 2. Leurs valeurs décimales sont classées en fonction des premiers chiffres du nombre.
Les premiers chiffres sont 1, puis tous les 10, puis tous les 11 puis tous les 12 …. Cela donne un classement très visuel où les puissances sont rangées par 10 sous la forme d’un sapin de noël.
| Rang | Puissance de 2 | Valeur |
| 0 | 2^0 | 1 |
| 1 | 2^10 | 1 024 |
| 2 | 2^20 | 1 048 576 |
| 3 | 2^30 | 1 073 741 824 |
| 4 | 2^40 | 1 099 511 627 776 |
| 5 | 2^50 | 1 125 899 906 842 620 |
| 6 | 2^60 | 1 152 921 504 606 850 000 |
| 7 | 2^70 | 1 180 591 620 717 410 000 000 |
| 8 | 2^80 | 1 208 925 819 614 630 000 000 000 |
| 9 | 2^90 | 1 237 940 039 285 380 000 000 000 000 |
| 10 | 2^7 | 128 |
| 11 | 2^17 | 131 072 |
| 12 | 2^27 | 134 217 728 |
| 13 | 2^37 | 137 438 953 472 |
| 14 | 2^47 | 140 737 488 355 328 |
| 15 | 2^57 | 144 115 188 075 856 000 |
| 16 | 2^67 | 147 573 952 589 676 000 000 |
| 17 | 2^77 | 151 115 727 451 829 000 000 000 |
| 18 | 2^87 | 154 742 504 910 673 000 000 000 000 |
| 19 | 2^97 | 158 456 325 028 529 000 000 000 000 000 |
| 20 | 2^4 | 16 |
| 21 | 2^14 | 16 384 |
| 22 | 2^24 | 16 777 216 |
| 23 | 2^34 | 17 179 869 184 |
| 24 | 2^44 | 17 592 186 044 416 |
| 25 | 2^54 | 18 014 398 509 482 000 |
| 26 | 2^64 | 18 446 744 073 709 600 000 |
| 27 | 2^74 | 18 889 465 931 478 600 000 000 |
| 28 | 2^84 | 19 342 813 113 834 100 000 000 000 |
| 29 | 2^94 | 19 807 040 628 566 100 000 000 000 000 |
| 30 | 2^1 | 2 |
| 31 | 2^11 | 2 048 |
| 32 | 2^21 | 2 097 152 |
| 33 | 2^31 | 2 147 483 648 |
| 34 | 2^41 | 2 199 023 255 552 |
| 35 | 2^51 | 2 251 799 813 685 250 |
| 36 | 2^61 | 2 305 843 009 213 690 000 |
| 37 | 2^71 | 2 361 183 241 434 820 000 000 |
| 38 | 2^81 | 2 417 851 639 229 260 000 000 000 |
| 39 | 2^91 | 2 475 880 078 570 760 000 000 000 000 |
| 40 | 2^8 | 256 |
| 41 | 2^18 | 262 144 |
| 42 | 2^28 | 268 435 456 |
| 43 | 2^38 | 274 877 906 944 |
| 44 | 2^48 | 281 474 976 710 656 |
| 45 | 2^58 | 288 230 376 151 712 000 |
| 46 | 2^68 | 295 147 905 179 353 000 000 |
| 47 | 2^78 | 302 231 454 903 657 000 000 000 |
| 48 | 2^88 | 309 485 009 821 345 000 000 000 000 |
| 49 | 2^98 | 316 912 650 057 057 000 000 000 000 000 |
| 50 | 2^5 | 32 |
| 51 | 2^15 | 32 768 |
| 52 | 2^25 | 33 554 432 |
| 53 | 2^35 | 34 359 738 368 |
| 54 | 2^45 | 35 184 372 088 832 |
| 55 | 2^55 | 36 028 797 018 964 000 |
| 56 | 2^65 | 36 893 488 147 419 100 000 |
| 57 | 2^75 | 37 778 931 862 957 200 000 000 |
| 58 | 2^85 | 38 685 626 227 668 100 000 000 000 |
| 59 | 2^95 | 39 614 081 257 132 200 000 000 000 000 |
| 60 | 2^2 | 4 |
| 61 | 2^12 | 4 096 |
| 62 | 2^22 | 4 194 304 |
| 63 | 2^32 | 4 294 967 296 |
| 64 | 2^42 | 4 398 046 511 104 |
| 65 | 2^52 | 4 503 599 627 370 500 |
| 66 | 2^62 | 4 611 686 018 427 390 000 |
| 67 | 2^72 | 4 722 366 482 869 650 000 000 |
| 68 | 2^82 | 4 835 703 278 458 520 000 000 000 |
| 69 | 2^92 | 4 951 760 157 141 520 000 000 000 000 |
| 70 | 2^9 | 512 |
| 71 | 2^19 | 524 288 |
| 72 | 2^29 | 536 870 912 |
| 73 | 2^39 | 549 755 813 888 |
| 74 | 2^49 | 562 949 953 421 312 |
| 75 | 2^59 | 576 460 752 303 423 000 |
| 76 | 2^69 | 590 295 810 358 706 000 000 |
| 77 | 2^79 | 604 462 909 807 315 000 000 000 |
| 78 | 2^89 | 618 970 019 642 690 000 000 000 000 |
| 79 | 2^99 | 633 825 300 114 115 000 000 000 000 000 |
| 80 | 2^6 | 64 |
| 81 | 2^16 | 65 536 |
| 82 | 2^26 | 67 108 864 |
| 83 | 2^36 | 68 719 476 736 |
| 84 | 2^46 | 70 368 744 177 664 |
| 85 | 2^56 | 72 057 594 037 927 900 |
| 86 | 2^66 | 73 786 976 294 838 200 000 |
| 87 | 2^76 | 75 557 863 725 914 300 000 000 |
| 88 | 2^86 | 77 371 252 455 336 300 000 000 000 |
| 89 | 2^96 | 79 228 162 514 264 300 000 000 000 000 |
| 90 | 2^3 | 8 |
| 91 | 2^13 | 8 192 |
| 92 | 2^23 | 8 388 608 |
| 93 | 2^33 | 8 589 934 592 |
| 94 | 2^43 | 8 796 093 022 208 |
| 95 | 2^53 | 9 007 199 254 740 990 |
| 96 | 2^63 | 9 223 372 036 854 780 000 |
| 97 | 2^73 | 9 444 732 965 739 290 000 000 |
| 98 | 2^83 | 9 671 406 556 917 030 000 000 000 |
| 99 | 2^93 | 9 903 520 314 283 040 000 000 000 000 |
H°/ 1k + 2k + 3k+ … +nk et les nombres de Bernoulli mais aussi le tout premier programme informatique :
En 1843, Ada Lovelace fabrique ce qui est considéré comme le tout premier programme informatique au temps où les ordinateurs n’existaient pas, sur la machine analytique de Charles Babbage de 1834 qui étaient une machine à calculer.
Pour cela son programme calcule les nombres de Bernoulli que l’on trouve dans les sommes des n premiers entiers à la puissance k.
Voici les formules des sommes des n premiers entiers à la puissance k.
S_{0}=1^{0}+2^{0}+3^{0}+...+n^{0}= 1n\\ S_{1}=1^{1}+2^{1}+3^{1}+...+n^{1}= \frac{1}{2}(n^{2}+n)\\ S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)\\ S_{3}=1^{3}+2^{3}+3^{3}+...+n^{3}= \frac{1}{4}(n^{4}+2n^{3}+n^{2}\hspace{2mm}+0n^{1})\\ S_{4}=1^{4}+2^{4}+3^{4}+...+n^{4}= \frac{1}{5}(n^{5}+\frac{5}{2}n^{4}+\frac{5}{3}n^{3}+0n^{2} - \frac{5}{6}n)\\ S_{5}=1^{5}+2^{5}+3^{5}+...+n^{5}= \frac{1}{6}(n^{6}+3n^{5}+\frac{5}{2}n^{4}+0n^{3} - \frac{1}{2}n^{2}+0n^{1})1°/ La somme des entiers : combien vaut la somme des n premiers entiers ?
Pour cela écrivons deux fois cette suite et additionnons-la.
. 1 + 2 + 3 + … + (n-2) + (n-1) + n
+ n + (n-1) + (n-2) + … + 3 + 2 + 1
(n+1) + (2 + n-1) + (3 + n-2) + … (n-2 + 3) + (2 + n-1) + (n+1) = n x (n + 1)
Donc la suite des n premiers entiers = S_{1} = \frac{n\times (n + 1))}{2}= \frac{1}{2}(n^{2}+n)
2°/ La somme des carrés : 12 + 22 + 33+ 42 + 52 = 55
Pour cela positionnons les nombres au carré dans un triangle comme ci-dessous. En effet il y a un 1 sur la 1ière ligne, puis deux 2 sur la 2ième, trois 3 sur la 3ième et ainsi de suite.
La somme de chaque case du triangle = 1×1 + 2×2 + 3×3 + 4×4 + 5×5 = 12 + 22 + 33+ 42 + 52
L’astuce pour déterminer une formule générale et d’additionner 3 de ces triangles.
En effet la somme de chaque case située à la même position dans chaque triangle donnera 11 car, comme l’indique les flèches bleues, quand on passe d’une case à celle en-dessous :
– dans le 1ier triangle, on ajoute 1.
– dans le 1ier triangle, on ne change rien.
– dans le 1ier triangle, on soustrait 1.
La somme de chaque case située à la même position est donc toujours la même.
Dans le cas général elle sera égale à : 1 + n + n = 2n + 1

Donc, dans le cas général :
1^{2}+2^{2}+3^{2}+...+n^{2}=(2n+1)\times \frac{n\times (n+1)}{2}\times \frac{1}{3}=\frac{(2n+1)\times(n^{2}+n)}{6}=\frac{2n^{3}+ 3n^{2}+ n}{6}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)Ainsi : S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)
3°/ La somme des cubes : 13 + 23 + 33+ 43 + 53 = 225
Cette fois-ci nous allons utiliser un carré pour trouver la formule générale, et plus exactement la table de multiplication.
En effet, si on découpe la table de 5 en forme de « L » inversé comme ci-dessous, chaque « L » représente le carré du nombre qui l’initie.
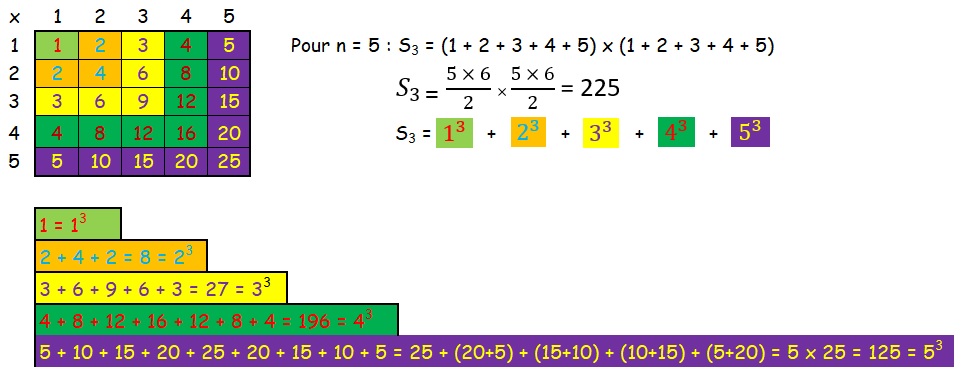
Donc, dans le cas général :
S_{3}=1^{3}+2^{3}+3^{3}+...+n^{3}= \left ( \frac{n\times (n + 1)}{2}\right )^{2} = \left ( \frac{n^{2}+n}{2}\right )^{2} =\frac{n^{4}+2n^{3}+n^{2}}{4}=\frac{1}{4}(n^{4}+2n^{3}+n^{2})Ainsi : S_{3}=1^{3}+2^{3}+3^{3}+...+n^{3}= \frac{1}{4}(n^{4}+2n^{3}+n^{2}+0n^{1})
4°/ Et dans le cas général ?
Avoir une formule pour déterminer chaque somme sans avoir a calculer ses membres est déjà superbe, mais n’avoir qu’une seule formule pour les calculer toutes serait digne du seigneur des anneaux !!
Résumons les formules jusqu’à la puissance 5.
S_{0}=1^{0}+2^{0}+3^{0}+...+n^{0}= 1n\\ S_{1}=1^{1}+2^{1}+3^{1}+...+n^{1}= \frac{1}{2}(n^{2}+n)\\ S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)\\ S_{3}=1^{3}+2^{3}+3^{3}+...+n^{3}= \frac{1}{4}(n^{4}+2n^{3}+n^{2}+0n^{1})\\ S_{4}=1^{4}+2^{4}+3^{4}+...+n^{4}= \frac{1}{5}(n^{5}+\frac{5}{2}n^{4}+\frac{5}{3}n^{3}+0n^{2} - \frac{5}{6}n)\\ S_{5}=1^{5}+2^{5}+3^{5}+...+n^{5}= \frac{1}{6}(n^{6}+3n^{5}+\frac{5}{2}n^{4}+0n^{3} - \frac{1}{2}n^{2}+0n^{1})Modifions les coefficients :
S_{0}=1^{0}+2^{0}+3^{0}+...+n^{0}= 1n\\S_{1}=1^{1}+2^{1}+3^{1}+...+n^{1}= \frac{1}{2}({\color{Red} \textbf{1}}n^{2}+{\color{Blue} \textbf{2}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{2}}}n)\\S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{1}{3}({\color{Red} \textbf{1}}n^{3}+{\color{Blue} \textbf{3}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{2}}}n^{2}+\hspace{2mm}{\color{Magenta} \textbf{3}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{6}}}n)\\S_{3}=1^{3}+2^{3}+3^{3}+...+n^{3}= \frac{1}{4}({\color{Red} \textbf{1}}n^{4}+{\color{Blue} \textbf{4}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{2}}}n^{3}+\hspace{2mm}{\color{Magenta} \textbf{6}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{6}}}n^{2}+\hspace{2mm}{\color{Green} \textbf{4}}\times {\color{DarkOrange} \textbf{0}}n^{1})\\S_{4}=1^{4}+2^{4}+3^{4}+...+n^{4}= \frac{1}{5}({\color{Red} \textbf{1}}n^{5}+{\color{Blue} \textbf{5}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{2}}}n^{4}+{\color{Magenta} \textbf{10}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{6}}}n^{3}+{\color{Green} \textbf{10}}\times {\color{DarkOrange} \textbf{0}}n^{2} +\hspace{2mm}{\color{Teal} \textbf{5}}\times {\color{DarkOrange} \frac{\textbf{-1}}{\textbf{30}}}n)\\S_{5}=1^{5}+2^{5}+3^{5}+...+n^{5}= \frac{1}{6}({\color{Red} \textbf{1}}n^{6}+{\color{Blue} \textbf{6}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{2}}}n^{5}+{\color{Magenta} \textbf{15}}\times {\color{DarkOrange} \frac{\textbf{1}}{\textbf{6}}}n^{4}+{\color{Green} \textbf{20}}\times {\color{DarkOrange} \textbf{0}}n^{3} + {\color{Teal} \textbf{15}}\times {\color{DarkOrange} \frac{\textbf{-1}}{\textbf{30}}}n^{2}+{\color{Yellow} \textbf{6}}\times {\color{DarkOrange} \textbf{0}}n^{1})\\Oui je sais cela devient tordue et bien compliqué, mais le miracle arrive !!
Récupérons les coefficients :
| {\color{Red} \textbf{1}}\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{2}}\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{3}}\hspace{3mm}{\color{Magenta} \textbf{3}}\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{4}}\hspace{3mm}{\color{Magenta} \textbf{6}}\hspace{4mm}{\color{Green} \textbf{4}}\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{5}}\hspace{2mm}{\color{Magenta} \textbf{10}}\hspace{2mm}{\color{Green} \textbf{10}}\hspace{2mm}{\color{Teal} \textbf{5}}\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{6}}\hspace{2mm}{\color{Magenta} \textbf{15}}\hspace{2mm}{\color{Green} \textbf{20}}\hspace{2mm}{\color{Teal} \textbf{15}}\hspace{2mm}{\color{Yellow} \textbf{6}}\\
Le triangle de Pascal sans les 1 finaux. |
1\\{\color{Red} \textbf{1}}\hspace{2mm}1\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{2}}\hspace{3mm}1\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{3}}\hspace{3mm}{\color{Magenta} \textbf{3}}\hspace{4mm}1\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{4}}\hspace{3mm}{\color{Magenta} \textbf{6}}\hspace{4mm}{\color{Green} \textbf{4}}\hspace{3mm}1\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{5}}\hspace{2mm}{\color{Magenta} \textbf{10}}\hspace{2mm}{\color{Green} \textbf{10}}\hspace{2mm}{\color{Teal} \textbf{5}}\hspace{4mm}1\\ {\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{6}}\hspace{2mm}{\color{Magenta} \textbf{15}}\hspace{2mm}{\color{Green} \textbf{20}}\hspace{2mm}{\color{Teal} \textbf{15}}\hspace{2mm}{\color{Yellow} \textbf{6}}\hspace{4mm}1\\{\color{Red} \textbf{1}}\hspace{2mm}{\color{Blue} \textbf{7}}\hspace{2mm}{\color{Magenta} \textbf{21}}\hspace{2mm}{\color{Green} \textbf{35}}\hspace{2mm}{\color{Teal} \textbf{35}}\hspace{2mm}{\color{Yellow} \textbf{21}}\hspace{2mm}{\color{Blue} \textbf{7}}\hspace{2mm}1\\ Le triangle de Pascal où un nombre est la somme des 2 qui sont au-dessus. |
| \times \hspace{0.5mm}\times\hspace{1.5mm}\times\hspace{2mm}\times\hspace{2mm}\times\hspace{2mm}\times | |
| {\color{DarkOrange} \textbf{1}\hspace{2mm}\frac{\textbf{1}}{\textbf{2}}\hspace{3mm}\frac{\textbf{1}}{\textbf{6}}\hspace{3mm}\textbf{0}\hspace{3mm}\frac{\textbf{-1}}{\textbf{30}}\hspace{3mm}\textbf{0}} | Les nombres de Bernoulli :
B_{0} = 1; B_{1} = \frac{1}{2}; B_{2} = \frac{1}{6}; B_{3} = 0; B_{4} = \frac{-1}{30}; B_{5} = 0; B_{6} = \frac{1}{42} |
Les formules des sommes des puissances des nombres entiers consécutifs combinent à la fois les nombres du triangle de Pascal et les nombres de Bernoulli.
Par cette méthode , si on connait un nombre de Bernoulli on peut déterminer le suivant. Calculons le 6ième B6.
La somme des carrés : S_{2}=1^{2}+...+n^{2}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n) = \frac{1}{3}(1B_{0}\times n^{3}+3B_{1}\times n^{2}+3B_{2}\times n)
On en déduit l’écriture des puissances de 6 : S_{6}=1^{6}+...+n^{6}= \frac{1}{7}(1B_{0}\times n^{7}+7B_{1}\times n^{6}+21B_{2}\times n^{5}+35B_{3}\times n^{4}+35B_{4}\times n^{3}+21B_{5}\times n^{2}+7B_{6}\times n^{1})
Si on prend n = 1 :
S_{6}=1^{6}= 1 = \frac{1}{7}(1B_{0}\times 1^{7}+7B_{1}\times 1^{6}+21B_{2}\times 1^{5}+35B_{3}\times 1^{4}+35B_{4}\times 1^{3}+21B_{5}\times 1^{2}+7B_{6}\times 1^{1})\\ S_{6}= 1 =\frac{1}{7}(B_{0}+7B_{1}+21B_{2}+35B_{3}+35B_{4}+21B_{5}+7B_{6})\\ S_{6}= 1 = \frac{1}{7}(1 + \frac{7}{2}+ \frac{21}{6}+0+\frac{-35}{30}+0+7B_{6})= \frac{1}{7} +\frac{1}{2}+\frac{1}{2}-\frac{1}{6}+B_{6} = \frac{41}{42}+B_{6}\\ B_{6}= 1 -\frac{41}{42}= \frac{1}{42}Ces formules rappellent étrangement les coefficients binomiaux des égalités remarques.
| 1 | (a + b) 0 = 1 |
| 1 1 | (a + b) 1 = 1a + 1b |
| 1 2 1 | (a + b) 2 = 1a² +2ab + 1b² |
| 1 3 3 1 | (a + b) 3 = 1a3 + 3a²b + 3ab² + 1b3 = 1a3b0 + 3a²b + 3ab² + 1a0b3 |
| 1 4 6 4 1 | (a + b) 4 = 1a4 + 4a3b + 6a²b² + 4ab3 + 1b4 |
| 1 5 10 10 5 1 | (a + b) 5 = 1a5 + 5a4b + 10a3b² + 10a²b3 + 5ab4 + 1b5 |
| 1 6 15 20 15 6 1 | (a + b) 6 = 1a6 + 6a5b + 15a4b² + 20a3b3 + 15a²b4 + 6ab5 + 1b6 |
Donc par exemple : (a + b) 3 = 1a3b0 + 3a²b + 3ab² + 1a0b3
Si on remplace a par un nombre de Bernoulli B et b par un nombre n : (n + B) 3 = 1n3B0 + 3n²B1 + 3nB2 + 1n0 = n3B0 + 3n²B1 + 3nB2 + B3
On arrive ici dans la rubrique bidouille, ou les régles d’algèbre classique sont un peu misent à mal :
– bidouille n°1 : Imaginons que B² soit égal au nombre de Bernoulli B2. Alors, des mathématiciens se sont penchés sur ce problème et de là est sortie le Calcul Ombral.
. (n + B) 3 = n3B0 + 3n²B1 + 3nB2 + B3
– bidouille n°2 : Dans le triangle de Pascal on n’utilise pas les 1 à la fin de chaque ligne, donc il faut faire passer le dernier membre B3 de l’autre coté de l’équation.
. (n + B) 3 – B3 = n3B0 + 3n²B1 + 3nB2
– bidouille n°3 : Il y a toujours devant les formules une fraction \frac{1}{n+1} pour les puissances de n.
Rappel : S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{1}{3}(n^{3}+\frac{3}{2}n^{2}+\frac{1}{2}n)=\frac{1}{3}(B_{0}n^{3}+3B_{1}\times n^{2}+3B_{2}\times n)\\ Donc : n^{3}B_{0}+3n^{2}B_{1}+3nB_{2} = 3S_{2}= (n + B)^{3}-B_{3}\\ Ainsi : S_{2}=1^{2}+2^{2}+3^{2}+...+n^{2}= \frac{(n + B)^{3}-B_{3}}{3}
Plus généralement : S_{k-1}=1^{k-1}+2^{k-1}+3^{k-1}+...+n^{k-1}= \frac{(n + B)^{k}-B_{k}}{k}
Où BK sera le nombre de Bernoulli Bk.
Vérification : 12 + 22 + 33+ 42 + 52 = 55 où : k = 3 et n = 5
1^{2}+2^{2}+3^{2}+4^{2}+5^{2}= \frac{(5 + B)^{3}-B_{3}}{3}=\frac{(125 +3\times 25B+3\times 5B^{2}+B^{3})-B^{3}}{3}\\ 1^{2}+2^{2}+3^{2}+4^{2}+5^{2}= \frac{(125+75\times \frac{1}{2}+15\times \frac{1}{6}+0)-0}{3}=\frac{165}{3}=55Bien entendue cette sublime formule ne prend tous sont sens que si n est trés grand car effectuer 1^{2}+2^{2}+3^{2}+...+150^{2} revient à calculer 150 carrés, alors qu’avec la formule :
1^{2}+2^{2}+3^{2}+...+150^{2}= \frac{(150 + B)^{3}-B_{3}}{3}=\frac{(3375000+3\times 22500B+3\times 150B^{2}+B^{3})-B^{3}}{3}\\ 1^{2}+2^{2}+3^{2}+...+150^{2}= \frac{(3375000+67500\times \frac{1}{2}+450\times \frac{1}{6}+0)-0}{3}=\frac{3408825}{3}=1136275
En 1843, sur la machine à calculer de Charles Babbage, Ada Lovelace fabrique ce qui est considéré comme le tout premier programme informatique au temps où les ordinateurs n’existaient pas.
En utilisant des fiches perforées à la manière d’un orgue de barbarie, cette machine était capable d’effectuer des calculs élémentaires mais aussi et surtout des boucles de calcul à l’instar de nos ordinateurs. Ada Lovelace pu ainsi calculer les nombres de Bernoulli à partir du nombre B3.
I°/ Les Cent mille milliards de poèmes :
En 1961, Raymond Queneau a écrit un ouvrage contenant 1014 de poèmes ….
A raison d’une minute par poème, il faudrait : \frac{10^{14} \ poemes \times 1 \ min}{365 \ jours \times 24 \ heures \times 60 \ min}=190 \ 258 \ 751 années.
Comment alors écrire un tel livre ?
Raymond Queneau a tout simplement écrit un sonnet de 14 vers de 2 quatrains et de 2 tercets (2×4 + 2×3 = 14 vers). Cependant il a fabriqué un livre comportant 10 versions de chaque vers. Ainsi en combinant chacune des 10 versions de ses 14 vers il a obtenue 10^{14} poèmes.
Voici un outil permettant de créer des poèmes à partir du recueil de Raymond Queneau. Il suffit de passer la souris sur les vers pour les modifier.
J°/ Ordre de grandeur :

3,1 x 10-11 = atome d’hydrogéne
1025 < taille en métre de l’univers connu.
1080 < nombre d’atomes de l’univers connu.
Il y a 43 252 003 274 489 856 000 positions possibles au Rubik’s cube.
Voici une animation qui permet de visualiser des objets de 10-35 à 1027 : Scale of Universe.
Et une autre vidéo impréssionnante qui zoome de l’infinimant petit vers l’infinimant grand.
Tentez d’évaluer les ordres de grandeurs suivantes dans ce petit programme Scatch :
K°/ Le nom des puissances :
Pour les puissances de 10.
|
10n |
Préfixe |
Symbole |
Nombre décimal |
Désignation |
Étymologie |
|
1030 |
Q |
1 000 000 000 000 000 000 000 000 000 000 |
|
Déformation du latin decem et du grec ancien δέκα, signifiant tous deux « dix » (pour symboliser 100010). |
|
|
1027 |
R |
1 000 000 000 000 000 000 000 000 000 |
|
Déformation du latin novem et du grec ancien ἐννέα, signifiant tous deux « neuf » (pour symboliser 10009). |
|
|
1024 |
Y |
1 000 000 000 000 000 000 000 000 |
du grec ὀϰτώ, huit. |
||
|
1021 |
Z |
1 000 000 000 000 000 000 000 |
de la lettre grecque ζ dzeta. |
||
|
1018 |
E |
1 000 000 000 000 000 000 |
Trillion |
du grec ἕξ, hexa, « six », car 1018 = 10006. |
|
|
1015 |
P |
1 000 000 000 000 000 |
du grec πέντε, penta, « cinq », car 1015 = 10005. |
||
|
1012 |
T |
1 000 000 000 000 |
du grec τέρας, teras, « monstre ». |
||
|
109 |
G |
1 000 000 000 |
du grec γίγας, gigas, « géant ». |
||
|
106 |
M |
1 000 000 |
du grec µέγας, megas, « grand ». |
||
|
103 |
k |
1 000 |
du grec χίλιοι, khilioi, « mille ». |
||
|
102 |
h |
100 |
du grec ἑκατόν, hekaton, « cent ». |
||
|
101 |
da |
10 |
du grec δέκα deka, « dix » |
||
|
100 |
(aucun) |
— |
1 |
(aucune) |
|
|
10−1 |
d |
0,1 |
Dixième |
du latin decimus, « dixième ». |
|
|
10−2 |
c |
0,01 |
Centième |
du latin centus, « cent ». |
|
|
10−3 |
m |
0,001 |
Millième |
du latin mille, « un millier ». |
|
|
10−6 |
µ |
0,000 001 |
Millionième |
du grec µικρός, mikros, « petit ». |
|
|
10−9 |
n |
0,000 000 001 |
Milliardième |
du grec νάνος, nanos, « nain ». |
|
|
10−12 |
p |
0,000 000 000 001 |
Billionième |
de l’italien piccolo, « petit ». |
|
|
10−15 |
f |
0,000 000 000 000 001 |
Billiardième |
du danois femten, « quinze », car 10−15. |
|
|
10−18 |
a |
0,000 000 000 000 000 001 |
Trillionième |
du danois atten, « dix-huit », car 10−18. |
|
|
10−21 |
z |
0,000 000 000 000 000 000 001 |
Trilliardième |
du latin septem, « sept », car 10−21 = 1000−7. |
|
|
10−24 |
y |
0,000 000 000 000 000 000 000 001 |
Quadrillionième |
du grec ὀκτώ, okto, « huit », car 10−24 = 1000−8. |
|
|
10−27 |
r |
0,000 000 000 000 000 000 000 000 001 |
|
Déformation du latin novem et du grec ancien ἐννέα, signifiant tous deux « neuf » (pour symboliser 1/10009). |
|
|
10−30 |
q |
0,000 000 000 000 000 000 000 000 000 001 |
|
Déformation du latin decem et du grec ancien δέκα, signifiant tous deux « dix » (pour symboliser 1/100010). |
Certaines puissances ont droit à leur petit nom : le carré pour x2 ou le cube pour x3. Mais le plus amusant est le zenzizenzizenzic qui est la puissance huitième d’un nombre. Ce terme est tombé en désuétude.
Le plus grand nombre qu’il soit possible d’écrire en lettres selon les conventions de la langue française en application de nos jours est :
neuf cent quatre-vingt-dix-neuf centilliards neuf cent quatre-vingt-dix-neuf centillions neuf cent quatre-vingt-dix-neuf noninonagintilliards neuf cent quatre-vingt-dix-neuf noninonagintillions neuf cent quatre-vingt-dix-neuf octononagintilliards neuf cent quatre-vingt-dix-neuf octononagintillions neuf cent quatre-vingt-dix-neuf septennonagintilliards neuf cent quatre-vingt-dix-neuf septennonagintillions neuf cent quatre-vingt-dix-neuf sexnonagintilliards neuf cent quatre-vingt-dix-neuf sexnonagintillions neuf cent quatre-vingt-dix-neuf quinnonagintilliards neuf cent quatre-vingt-dix-neuf quinnonagintillions neuf cent quatre-vingt-dix-neuf quattuornonagintilliards neuf cent quatre-vingt-dix-neuf quattuornonagintillions neuf cent quatre-vingt-dix-neuf trénonagintilliards neuf cent quatre-vingt-dix-neuf trénonagintillions neuf cent quatre- vingt-dix-neuf duononagintilliards neuf cent quatre- vingt-dix-neuf duononagintillions neuf cent quatre- vingt-dix-neuf unnonagintilliards neuf cent quatre-vingt-dix-neuf unnonagintillions neuf cent quatre-vingt-dix-neuf nonagintilliards neuf cent quatre-vingt-dix-neuf nonagintillions neuf cent quatre-vingt-dix-neuf nonioctogintilliards neuf cent quatre-vingt-dix-neuf nonioctogintillions neuf cent quatre-vingt-dix-neuf octooctogintilliards neuf cent quatre-vingt-dix-neuf octooctogintillions neuf cent quatre-vingt-dix-neuf septenoctogintilliards neuf cent quatre- vingt-dix-neuf septenoctogintillions neuf cent quatre-vingt-dix-neuf sexoctogintilliards neuf cent quatre- vingt-dix-neuf sexoctogintillions neuf cent quatre- vingt-dix-neuf quinoctogintilliards neuf cent quatre- vingt-dix-neuf quinoctogintillions neuf cent quatre-vingt-dix-neuf quattuoroctogintilliards neuf cent quatre- vingt-dix-neuf quattuoroctogintillions neuf cent quatre-vingt-dix-neuf tréoctogintilliards neuf cent quatre- vingt-dix-neuf tréoctogintillions neuf cent quatre- vingt-dix-neuf duooctogintilliards neuf cent quatre- vingt-dix-neuf duooctogintillions neuf cent quatre-vingt-dix-neuf unoctogintilliards neuf cent quatre-vingt-dix-neuf unoctogintillions neuf cent quatre-vingt-dix-neuf octogintilliards neuf cent quatre-vingt-dix-neuf octogintillions neuf cent quatre-vingt-dix-neuf noniseptuagintilliards neuf cent quatre-vingt-dix-neuf noniseptuagintillions neuf cent quatre-vingt-dix-neuf octoseptuagintilliards neuf cent quatre-vingt-dix-neuf octoseptuagintillions neuf cent quatre-vingt-dix-neuf septenseptuagintilliards neuf cent quatre-vingt-dix-neuf septenseptuagintillions neuf cent quatre-vingt-dix-neuf sexseptuagintilliards neuf cent quatre-vingt-dix-neuf sexseptuagintillions neuf cent quatre-vingt-dix-neuf quinseptuagintilliards neuf cent quatre-vingt-dix-neuf quinseptuagintillions neuf cent quatre-vingt-dix-neuf quattuorseptuagintilliards neuf cent quatre-vingt-dix-neuf quattuorseptuagintillions neuf cent quatre-vingt-dix-neuf tréseptuagintilliards neuf cent quatre-vingt-dix-neuf tréseptuagintillions neuf cent quatre-vingt-dix-neuf duoseptuagintilliards neuf cent quatre-vingt-dix-neuf duoseptuagintillions neuf cent quatre-vingt-dix-neuf unseptuagintilliards neuf cent quatre-vingt-dix-neuf unseptuagintillions neuf cent quatre-vingt-dix-neuf septuagintilliards neuf cent quatre-vingt-dix-neuf septuagintillions neuf cent quatre- vingt-dix-neuf nonisexagintilliards neuf cent quatre-vingt- dix-neuf nonisexagintillions neuf cent quatre-vingt-dix-neuf octosexagintilliards neuf cent quatre-vingt-dix-neuf octosexagintillions neuf cent quatre-vingt-dix-neuf septensexagintilliards neuf cent quatre-vingt-dix-neuf septensexagintillions neuf cent quatre-vingt-dix-neuf sexsexagintilliards neuf cent quatre-vingt-dix-neuf sexsexagintillions neuf cent quatre-vingt-dix-neuf quinsexagintilliards neuf cent quatre-vingt-dix-neuf quinsexagintillions neuf cent quatre-vingt-dix-neuf quattuorsexagintilliards neuf cent quatre-vingt-dix-neuf quattuorsexagintillions neuf cent quatre-vingt-dix-neuf trésexagintilliards neuf cent quatre-vingt-dix-neuf trésexagintillions neuf cent quatre-vingt-dix-neuf duosexagintilliards neuf cent quatre-vingt-dix-neuf duosexagintillions neuf cent quatre-vingt-dix-neuf unsexagintilliards neuf cent quatre-vingt-dix-neuf unsexagintillions neuf cent quatre-vingt-dix-neuf sexagintilliards neuf cent quatre-vingt-dix-neuf sexagintillions neuf cent quatre-vingt-dix-neuf noniquinquagintilliards neuf cent quatre-vingt-dix-neuf noniquinquagintillions neuf cent quatre-vingt-dix-neuf octoquinquagintilliards neuf cent quatre-vingt-dix-neuf octoquinquagintillions neuf cent quatre-vingt-dix-neuf septenquinquagintilliards neuf cent quatre-vingt-dix-neuf septenquinquagintillions neuf cent quatre-vingt-dix-neuf sexquinquagintilliards neuf cent quatre-vingt-dix-neuf sexquinquagintillions neuf cent quatre-vingt-dix-neuf quinquinquagintilliards neuf cent quatre-vingt-dix-neuf quinquinquagintillions neuf cent quatre-vingt-dix-neuf quattuorquinquagintilliards neuf cent quatre-vingt-dix-neuf quattuorquinquagintillions neuf cent quatre-vingt-dix-neuf tréquinquagintilliards neuf cent quatre-vingt-dix-neuf tréquinquagintillions neuf cent quatre-vingt-dix-neuf duoquinquagintilliards neuf cent quatre-vingt-dix-neuf duoquinquagintillions neuf cent quatre-vingt-dix-neuf unquinquagintilliards neuf cent quatre-vingt-dix-neuf unquinquagintillions neuf cent quatre-vingt-dix-neuf quinquagintilliards neuf cent quatre-vingt-dix-neuf quinquagintillions neuf cent quatre-vingt-dix-neuf noniquadragintilliards neuf cent quatre-vingt-dix-neuf noniquadragintillions neuf cent quatre-vingt-dix-neuf octoquadragintilliards neuf cent quatre-vingt-dix-neuf octoquadragintillions neuf cent quatre-vingt-dix-neuf septenquadragintilliards neuf cent quatre-vingt-dix-neuf septenquadragintillions neuf cent quatre-vingt-dix-neuf sexquadragintilliards neuf cent quatre-vingt-dix-neuf sexquadragintillions neuf cent quatre-vingt-dix-neuf quinquadragintilliards neuf cent quatre-vingt-dix-neuf quinquadragintillions neuf cent quatre-vingt-dix-neuf quattuorquadragintilliards neuf cent quatre-vingt-dix-neuf quattuorquadragintillions neuf cent quatre-vingt-dix-neuf tréquadragintilliards neuf cent quatre-vingt-dix-neuf tréquadragintillions neuf cent quatre-vingt-dix-neuf duoquadragintilliards neuf cent quatre-vingt-dix-neuf duoquadragintillions neuf cent quatre-vingt-dix-neuf unquadragintilliards neuf cent quatre-vingt-dix-neuf unquadragintillions neuf cent quatre-vingt-dix-neuf quadragintilliards neuf cent quatre-vingt-dix-neuf quadragintillions neuf cent quatre-vingt-dix-neuf nonitrigintilliards neuf cent quatre-vingt- dix-neuf nonitrigintillions neuf cent quatre-vingt-dix-neuf octotrigintilliards neuf cent quatre-vingt-dix-neuf octotrigintillions neuf cent quatre-vingt-dix-neuf septentrigintilliards neuf cent quatre-vingt-dix-neuf septentrigintillions neuf cent quatre-vingt-dix-neuf sextrigintilliards neuf cent quatre-vingt-dix-neuf sextrigintillions neuf cent quatre-vingt-dix-neuf quintrigintilliards neuf cent quatre-vingt-dix-neuf quintrigintillions neuf cent quatre-vingt-dix-neuf quattuortrigintilliards neuf cent quatre-vingt-dix-neuf quattuortrigintillions neuf cent quatre-vingt-dix-neuf trétrigintilliards neuf cent quatre-vingt-dix-neuf trétrigintillions neuf cent quatre- vingt-dix-neuf duotrigintilliards neuf cent quatre-vingt-dix-neuf duotrigintillions neuf cent quatre-vingt-dix-neuf untrigintilliards neuf cent quatre-vingt-dix-neuf untrigintillions neuf cent quatre-vingt-dix-neuf trigintilliards neuf cent quatre-vingt-dix-neuf trigintillions neuf cent quatre-vingt-dix-neuf nonivigintilliards neuf cent quatre- vingt-dix-neuf nonivigintillions neuf cent quatre-vingt-dix-neuf octovigintilliards neuf cent quatre-vingt-dix- neuf octovigintillions neuf cent quatre-vingt-dix-neuf septenvigintilliards neuf cent quatre-vingt-dix-neuf septenvigintillions neuf cent quatre-vingt-dix-neuf sexvigintilliards neuf cent quatre-vingt-dix-neuf sexvigintillions neuf cent quatre-vingt-dix-neuf quinvigintilliards neuf cent quatre-vingt-dix-neuf quinvigintillions neuf cent quatre-vingt-dix-neuf quattuorvigintilliards neuf cent quatre- vingt-dix-neuf quattuorvigintillions neuf cent quatre-vingt-dix-neuf trévigintilliards neuf cent quatre-vingt-dix-neuf trévigintillions neuf cent quatre-vingt-dix-neuf duovigintilliards neuf cent quatre-vingt-dix-neuf duovigintillions neuf cent quatre-vingt-dix-neuf unvigintilliards neuf cent quatre-vingt-dix-neuf unvigintillions neuf cent quatre-vingt-dix-neuf vigintilliards neuf cent quatre-vingt-dix-neuf vigintillions neuf cent quatre-vingt-dix-neuf nonidécilliards neuf cent quatre-vingt-dix-neuf nonidécillions neuf cent quatre-vingt-dix-neuf octodécilliards neuf cent quatre-vingt-dix-neuf octodécillions neuf cent quatre-vingt-dix-neuf septendécilliards neuf cent quatre-vingt-dix-neuf septendécillions neuf cent quatre- vingt-dix-neuf sexdécilliards neuf cent quatre-vingt-dix-neuf sexdécillions neuf cent quatre-vingt-dix-neuf quindécilliards neuf cent quatre-vingt-dix-neuf quindécillions neuf cent quatre-vingt-dix-neuf quattuordécilliards neuf cent quatre-vingt-dix-neuf quattuordécillions neuf cent quatre-vingt-dix-neuf trédécilliards neuf cent quatre-vingt-dix-neuf trédécillions neuf cent quatre-vingt-dix-neuf duodécilliards neuf cent quatre-vingt-dix-neuf duodécillions neuf cent quatre-vingt-dix-neuf undécilliards neuf cent quatre-vingt-dix-neuf undécillions neuf cent quatre-vingt-dix-neuf décilliards neuf cent quatre-vingt-dix-neuf décillions neuf cent quatre-vingt-dix-neuf nonilliards neuf cent quatre-vingt-dix-neuf nonillions neuf cent quatre-vingt-dix-neuf octilliards neuf cent quatre-vingt-dix-neuf octillions neuf cent quatre-vingt-dix-neuf septilliards neuf cent quatre-vingt-dix-neuf septillions neuf cent quatre-vingt-dix-neuf sextilliards neuf cent quatre-vingt-dix-neuf sextillions neuf cent quatre-vingt-dix-neuf quintilliards neuf cent quatre-vingt-dix-neuf quintillions neuf cent quatre-vingt-dix-neuf quadrilliards neuf cent quatre-vingt-dix-neuf quadrillions neuf cent quatre-vingt-dix-neuf trilliards neuf cent quatre-vingt-dix-neuf trillions neuf cent quatre-vingt-dix-neuf billiards neuf cent quatre-vingt-dix-neuf billions neuf cent quatre-vingt-dix-neuf milliards neuf cent quatre-vingt-dix-neuf millions neuf cent quatre-vingt-dix-neuf mille neuf cent quatre-vingt-dix-neuf.
En utilisant des notations mathématiques, il est également possible d’écrire ce nombre 10606 − 1.
L°/ Les épidémies :
La dernière épidémie de COVID nous a rappelé l’importance des Mathématiques pour modéliser les maladies.
Le R0 (prononcez « R zéro ») est le nombre de reproduction de base. Il indique le nombre moyen de nouveaux cas d’une maladie, qu’une seule personne infectée et contagieuse va générer en moyenne dans une population sans aucune immunité que l’on appelle personnes susceptibles.
R0 = 2 signifie que une personne infectée va infecter en moyenne 2 nouvelles personnes, qui elles-mêmes vont infecter 2 autres personnes.
La contamination est donc exponentielle, et on doit réduire ce R0 par du confimenement ou des vaccins.
Le R0 dépend principalement de trois facteurs :
- la durée de la contagiosité après infection ;
- la probabilité d’une infection après un contact entre une personne infectée et une personne susceptible ;
- la fréquence des contacts humains.
Plus ces trois facteurs sont élevés, plus le R0 sera important. Si celui-ci reste inférieur à 1, l’agent pathogène infectera moins d’une personne en moyenne par cas, et finira par disparaître. En revanche, si le R0 est supérieur à 1, cela signifie que le pathogène réussira à infecter davantage d’hôtes, provoquant une épidémie.
Pour les puissances de 10.
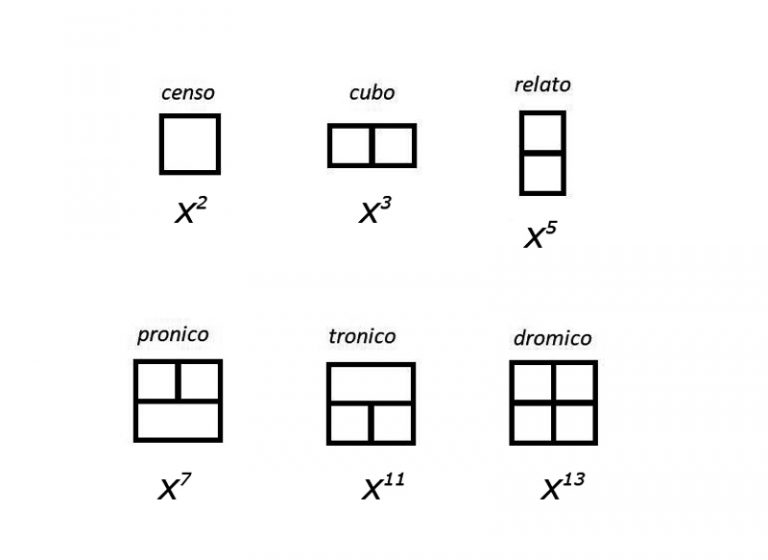
 M°/ Notation ancienne :
M°/ Notation ancienne :
Il s’agit d’un ensemble de symboles développés pour les puissances premières par le mathématicien italien Francesco Ghaligai en 1521 . Ceux-ci ont été utilisés là où nous utiliserions aujourd’hui une variable nommée et une puissance.