En Chine, au Ier millénaire avant notre ère, dans le Yi Jing, Le Livre des mutations, on trouve bien des histoires sur les nombres. Cet ouvrage, le premier des cinq classiques chinois, aura une influence considérable sur la pensée de l’empire du Milieu, dans les siècles qui suivront et jusqu’à nos jours. On trouve dans ce livre, la légende de Lo Shu qui rapporte que, pour calmer la colère de la rivière Lo, les riverains lui offrirent un bœuf en sacrifice ; ils virent alors sortir des flots une tortue dont la carapace était marquée d’une série de signes étranges. Si l’on compte le nombre de points de chaque symbole et qu’on les réécrit, en gardant la même disposition, dans les cases d’un carré 3 × 3, on obtient ceci :
 |
Cette disposition des nombres de 1 à 9 est particulièrement frappante. Vous pouvez vérifier que les sommes des nombres situés sur chaque ligne, chaque colonne et chaque diagonale sont toutes les mêmes, c’est-à-dire 15. À rotations et symétries près, cette disposition est la seule vérifiant cette propriété. Un tel tableau porte aujourd’hui le nom de carré magique. Le Lo Shu est le tout premier carré magique de l’histoire, mais il aura de nombreux successeurs. |
Un carré magique est un tableau carré sur lequel on dispose des nombres qui se suivent mais dans le désordre. Ces nombres sont disposés de sorte que leurs sommes sur chaque rangée, sur chaque colonne et sur chaque diagonale principale soient égales. On nomme alors constante magique (et parfois densité) la valeur de ces sommes.
Le jeu consiste à enlever quelques nombres et de demander de les retrouver.
Il existe plusieurs méthodes pour construire des carrés magiques impairs, c’est à dire que le nombre de case par côtés est impair (il est plus difficile de faire des carrés magiques pairs) :
I°/ Méthode de Edouard Lucas : XIXième siècle
II°/ Méthode de Bachet de Méziriac : XVIième siècle
III°/ Méthode du cavalier :
IV°/ Le tour de magie :
V°/ Le Carré magique de Ramanujan : Carré magique 4×4 avec sa date de naissance
VI°/ Des carrés magiques géométriques :
VII°/ Des carrés magiques circulaires :
VIII°/ Les formules :
IX°/ Carrés magiques et symétrie :
Une très belle vidéo en anglais :
I°/ Méthode de Edouard Lucas : XIXième siècle
En 1891 Edouard Lucas a proposé une méthode simple pour créer des carrés magiques de dimension 3.
| On choisit trois nombres entiers a, b et c tels que : 0 < a < b < c − a avec b ≠ 2.a
Puis on place dans le tableau les valeurs obtenues à partir des relations indiquées en cochant la case « Formules ». On voit que les somme des lignes, des colonnes et des diagonales valent toutes 3.c. |
II°/ Méthode de Bachet de Méziriac :
Voici une méthode plutôt simple mise au point par Bachet de Méziriac.
 |
 |
 |
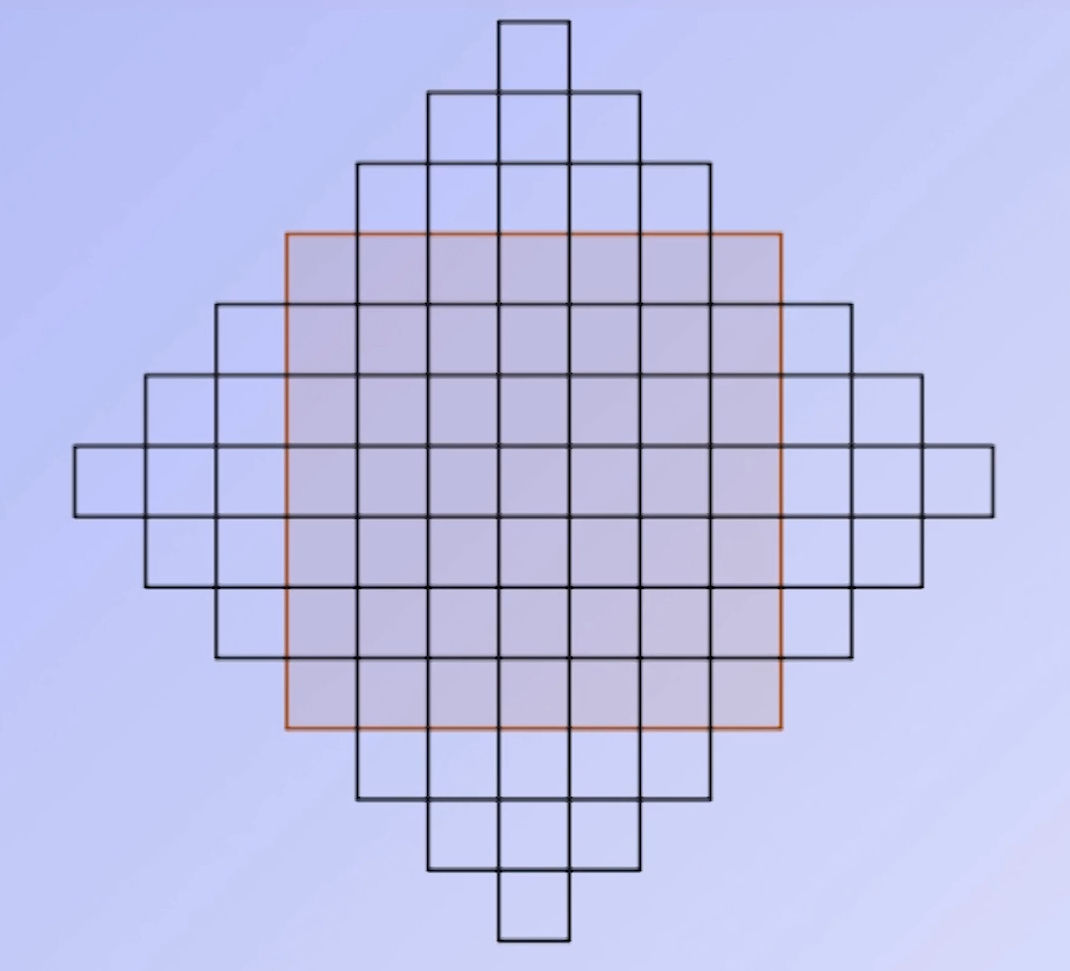
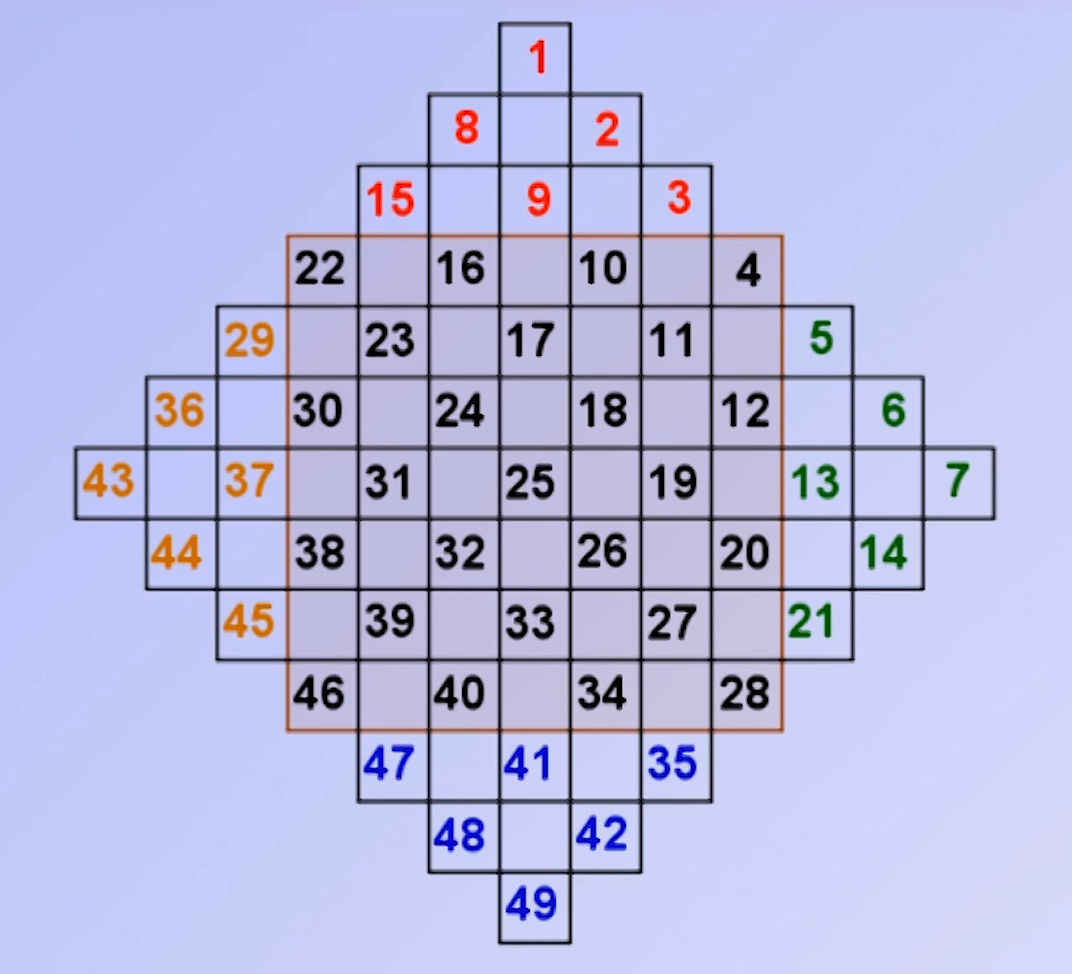
| On étend le carré de base par des cases supplémentaires comme ci-dessus, en diminuant de 1 le nombre de cases pour chaque lignes supplémentaires.. | On remplit le carré en commençant par la case qui est tout en haut et en remplissant une diagonale sur deux en mettant les nombres dans l’ordre. Il n’est pas nécessaire de commencer par le nombre 1. | On complète le carré en faisant descendre les nombres rouges en bas, les bleus en haut, les verts à gauche et les oranges à droite. Le carré est terminé. |
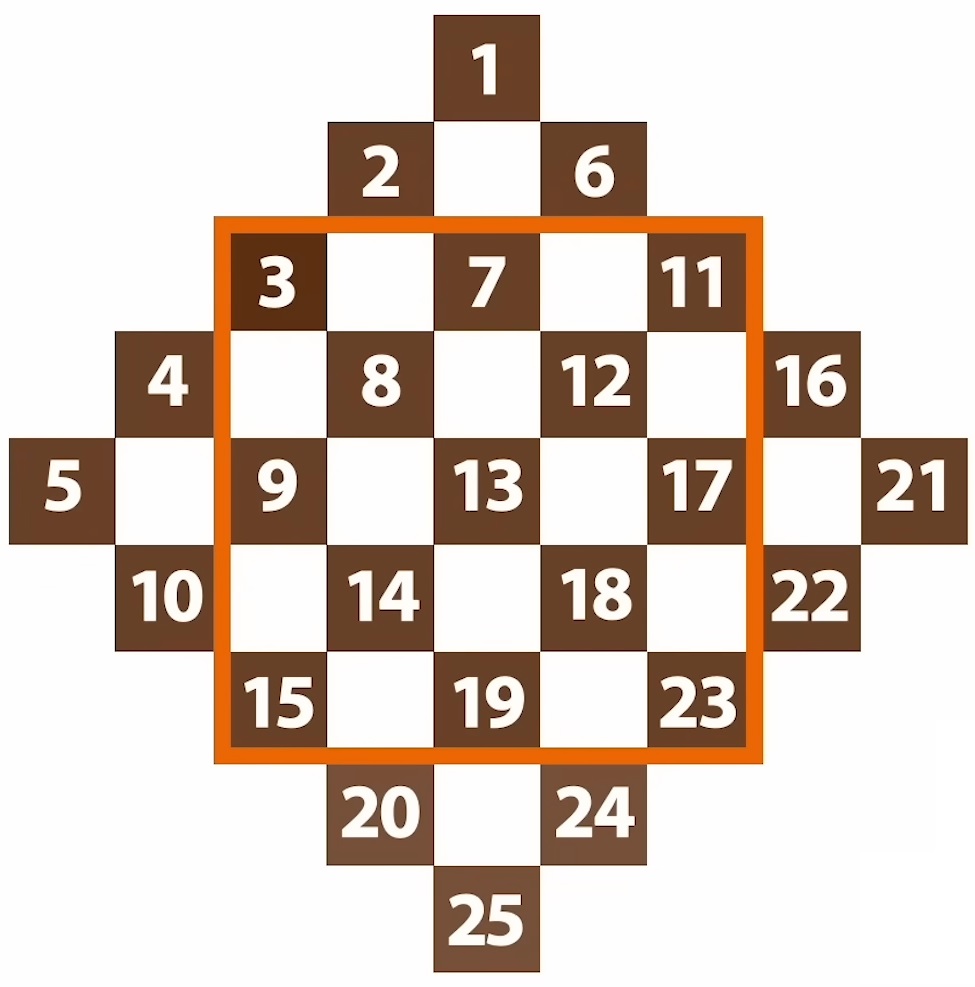
Voici une démonstration de cette méthode sur un carré de 5×5 :
 |
 |
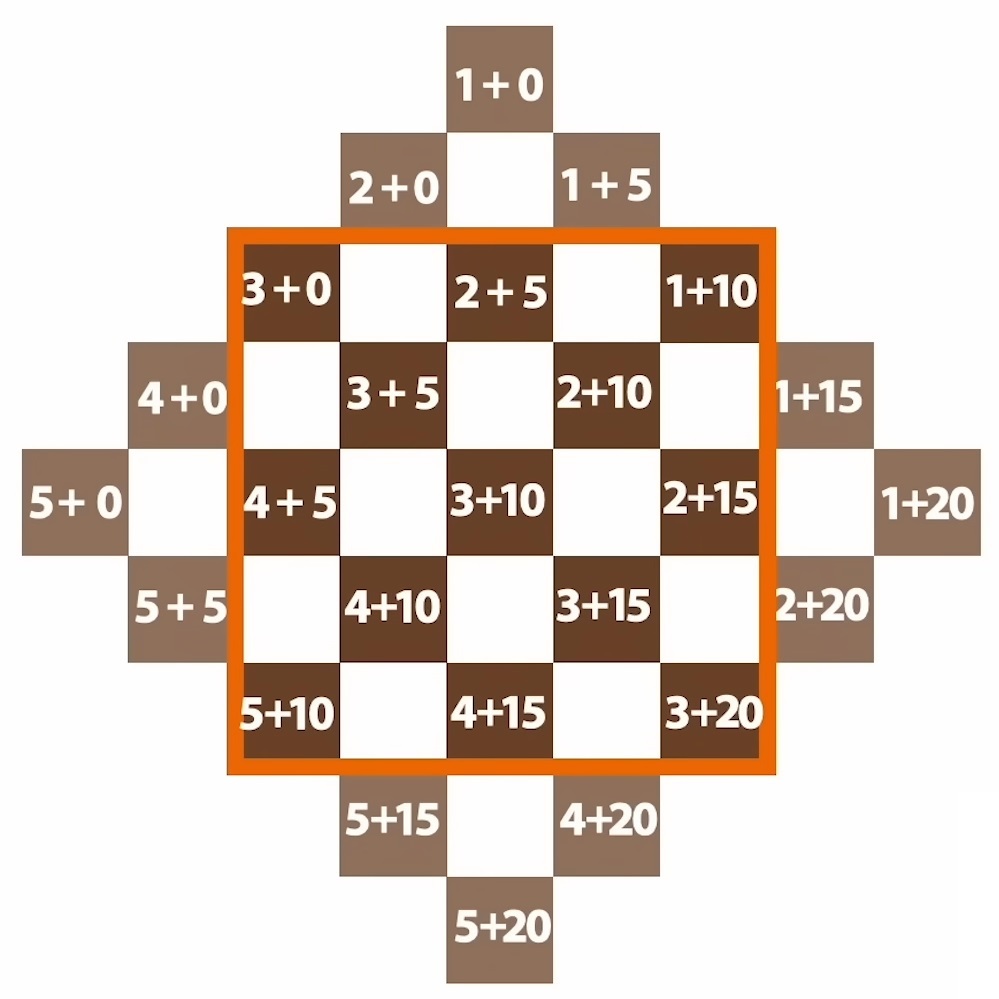 |
| Voici un carré magique 5×5. | Utilisons la technique de construction de Méziriac. | Remarquons que l’on passe d’une diagonale à celle en-dessous en ajoutant 5. |
 |
 |
|
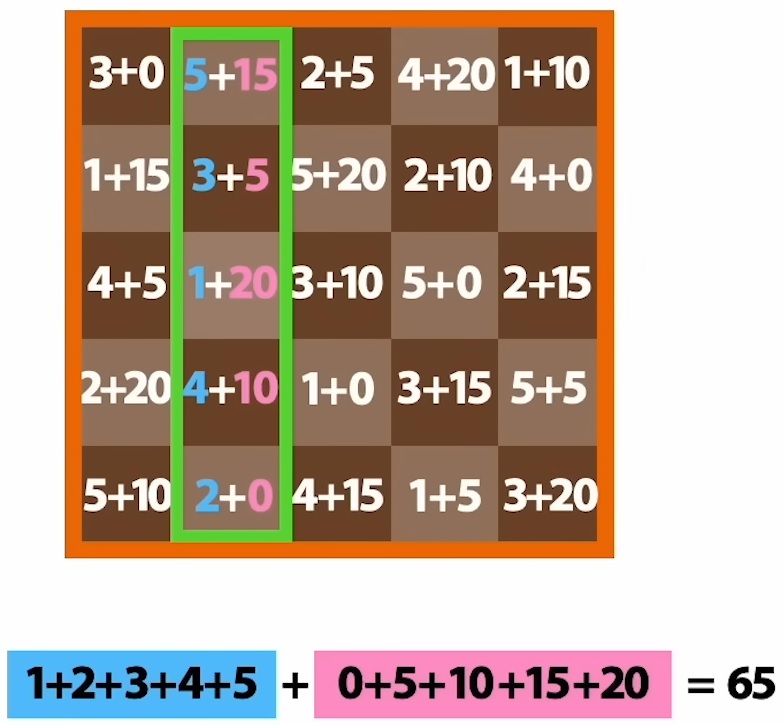
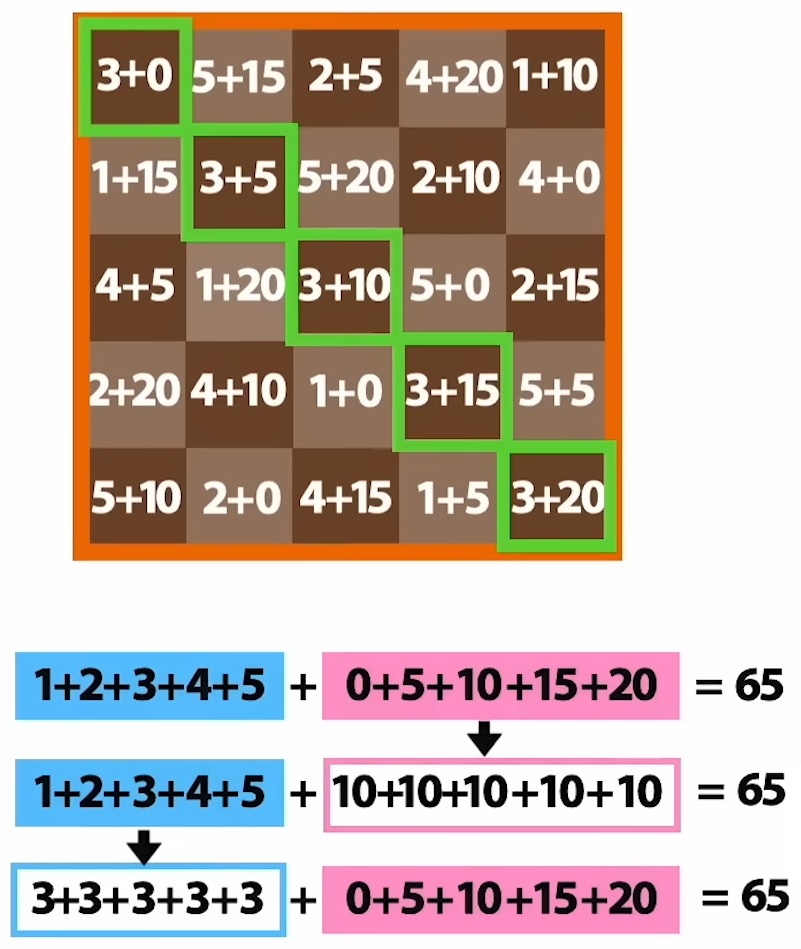
| En reconstituant le carré magique, on remarque que chaque ligne et chaque colonne comporte les nombres 1, 2, 3, 4 et 5 d’une part et 0, 5, 10, 15 et 20 d’autre part. La somme de tous ces nombres donnant 65. | Pour les diagonales les nombres seront (1, 2, 3, 4 et 5) et 5 fois le nombre 10, ou alors 5 fois le nombre 3 et (0, 5, 10, 15 et 20). La somme faisant toujours 65. |
Il facile de trouver la constante magique. En effet elle est égale à la somme des nombres du carré divisé par l’ordre du carré, c’est à dire le nombre de case des côtés.
Pour un carré magique d’ordre n : Constante \ magique = \frac{nombre \ de \ termes \times (premier \ terme+dernier \ terme)}{2n}
Une fois que l’on a construit un carré magique , il suffit d’effectuer une rotation d’un quart de tour pour en fabriquer trois autres et même d’effectuer une symétrie axiale des quatre carré pour en fabriquer quatre autres. Nous voici avec huit carrés magiques.
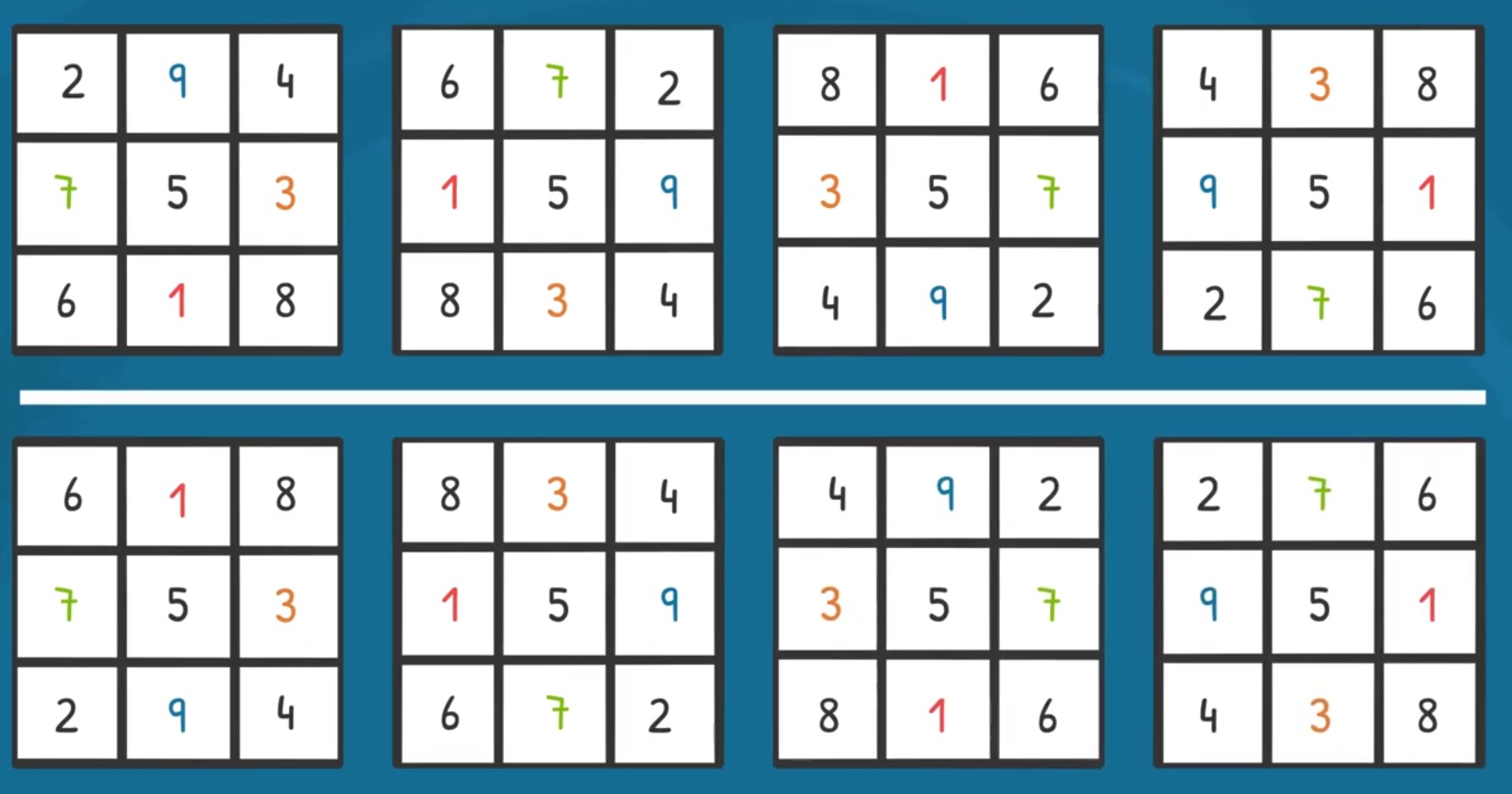
Remarquons que le nombre central, ici 5, ne change pas. Il s’agit du nombre central de la suite (1,2,3,4,5,6,7,8,9) et la moyenne des nombres de la suite ((1,2,3,4,5,6,7,8,9)/9 = 5).
Pour aller plus loin, on peut se servir des carrés magiques additifs pour construire des carrés magiques multiplicatifs, on on multiplie au lieu d’additionner.
Ici : 16 x 2048 x 64 = 2 097 152

Et les carrés magiques d’ordre pair me direz-vous. En voici un gravé sur un temple Indien.
 |
Le temple Parshvanath Jain à Khajuraho, en Inde, possède un remarquable carré magique le plus parfait.
Il contient les nombres 1 à 4² et possède deux propriétés extraordinaires :
– la somme magique est 34 = 2(4² + 1).
– tous les sous-carrés 2×2font aussi 34.
|
Un autre carré d’ordre 4 :
| 1 | 16 | 10 | 7 |
| 6 | 11 | 13 | 4 |
| 15 | 2 | 8 | 9 |
| 12 | 5 | 3 | 14 |
La constante magique est de 1 + 16 + 10 + 7 = 34.
Si on veut fabriquer un autre carré magique de constante magique 70, il suffit d’ajouter 70 – 34 = 36 aux nombres 1, 2, 3 et 4. Ce qui donne.
| 37 | 16 | 10 | 7 |
| 6 | 11 | 13 | 40 |
| 15 | 38 | 8 | 9 |
| 12 | 5 | 39 | 14 |
Une vidéo pour tout expliquer :
III°/ Méthode du cavalier :
| Un carré magique est un tableau carré de côté N qui est rempli par la suite des entiers de 1 à N2 afin que la somme des termes de toutes les lignes et de toutes les colonnes soient égales à Mn. Quand la somme des diagonales est également égale à Mn le carré est dit diabolique. Pour les carrés de côté impair, il existe un algorithme simple qui permet la construction des carrés magiques et diaboliques : c’est la méthode du cavalier (du jeu d’échec) découverte par Euler. Description : On choisit une case de départ arbitraire à ligne I et à la colonne J et on y place le nombre 1. On choisit les pas du cavalier (déplacement vers le bas de H lignes et vers la droite de K colonnes) et on inscrit dans chaque case atteinte l’entier suivant. Quand le déplacement amène en dehors du damier, on y continue sur la même ligne mais de l’autre coté. Si après N opérations, on retombe dans une case déjà occupée. Au lieu du déplacement normal, on se déplace alors de L lignes vers le bas et de M colonnes vers la droite. On reprend ensuite la marche normale. Conditions sur les valeurs H, K, L et M : Il faut que les couples (H, K) et (L, M) soient différents. Il faut que H, K, L et M soient tous premiers avec N. Il faut que le nombre (M x H − K x L) soit premier avec N. Si de plus les nombres (H + K), (H − K), (L + M) et (L − M) sont premiers avec N alors le carré est diabolique. Utilisation : Le programme permet la détermination et l’affichage de carrés magiques d’ordre impair. La valeur de Mn est également affichée. Les valeurs de N, I et J sont contrôlées par le programme. Il vous appartient de rentrer des valeurs de H, K, L et M valides. L’entrée de valeur incorrectes conduit à un carré qui contient des 0. H = 1, K = 2, L = 0 et M = −1 conduisent toujours sauf pour N multiple de 3 à un carré diabolique.Montrer que Mn = ½.n.(n2 + 1)
Référence : Le livre de René Descombes « Les carrés magiques » (éditions Vuibert 09-2000) constitue une bible pour les amateurs de carrés magiques. |
– Placer le 1er nombre au milieu de la 1ere ligne.
– Continuer en ajoutant 1 au 1er nombre. Placer ce nombre dans la case du coin supérieur droit.
– Si cette case est vide : Si on est à la 1ere ligne, il faut repartir à la dernière case de la colonne suivante.
. Si on est à la dernière colonne, il faut repartir à la 1ere case de la ligne supérieure.
. Si on tombe sur une case occupée, il faut repartir de la case située en dessous.
– La somme magique est : n(n²+1)/2.
Lorsque nous avons un carré de n cases sur n cases de côté, nous utilisons les n² premiers nombres entiers dont la somme est n² (n²+1)/2
Les n lignes ont chacune la même somme qui est donc égale au résultat précédent divisé par n soit à n(n²+1)/2.
Par exemple si n = 4, la somme magique est 4(16+1)/2 = 4(17)/2 = 34.
Les nombres représentent la position de chaque case.
|
47 |
58 |
69 |
80 |
1 |
12 |
23 |
34 |
45 |
|
57 |
68 |
79 |
9 |
11 |
22 |
33 |
44 |
46 |
|
67 |
78 |
8 |
10 |
21 |
32 |
43 |
54 |
56 |
|
77 |
7 |
18 |
20 |
31 |
42 |
53 |
55 |
66 |
|
6 |
17 |
19 |
30 |
41 |
52 |
63 |
65 |
76 |
|
16 |
27 |
29 |
40 |
51 |
62 |
64 |
75 |
5 |
|
26 |
28 |
39 |
50 |
61 |
72 |
74 |
4 |
15 |
|
36 |
38 |
49 |
60 |
71 |
73 |
3 |
14 |
25 |
|
37 |
48 |
59 |
70 |
81 |
2 |
13 |
24 |
35 |
|
17 |
24 |
1 |
8 |
15 |
|
23 |
5 |
7 |
14 |
16 |
|
4 |
6 |
13 |
20 |
22 |
|
10 |
12 |
19 |
21 |
3 |
|
11 |
18 |
25 |
2 |
9 |
|
8 |
1 |
6 |
|
3 |
5 |
7 |
|
4 |
9 |
2 |


IV°/ Le tour de magie :
Il serait amusant de fabriquer un carré magique façon mentaliste. Et bien c’est possible en apprenant un petit tableau.
Demander un votre assistance de choisir un nombre y compris entre 22 et 99, et vous voilà prêt à construire un tableau magique correspondant à ce nombre.
|
Il est nécessaire d’apprendre ce tableau par cœur et d’effectuer les calculs qui sont assez simples. On peut aussi l’avoir sous la main. Un peu de cinéma pour perdre un peu les spectateurs et le tour est joué. |
L’explication :
| Verticalement | Horizontalement | Diagonales |
| y – 20 + 11 + 5 + 4 = y 1 + 8 + 10 + y – 20 + 1 = y 12 + y – 20 – 1 + 3 + 6 = y 7 + 2 + y – 20 + 2 + 9 = y |
y – 20 + 1 + 12 + 7 = y 11 + 8 + y – 20 – 1 + 2 = y 5 + 10 + 3 + y – 20 + 2 = y 4 + y – 20 + 1 + 6 + 9 = y |
y – 20 + 8 + 3 + 9 = y 7 + y – 20 – 1 + 10 + 4 = y |
V°/ Le Carré magique de Ramanujan : Carré magique 4×4 avec sa date de naissance
Ramanujan était un célèbre Mathématicien indien considéré comme un génie des Mathématiques. Il a entre autre inventé un carré magique qui donne 139 non seulement en additionnant les lignes, les colonnes et les diagonales, mais aussi de bien d’autres façons. Petite cerise sur le gâteau qui rend ce carré bien plus que magique, Ramanujan est né le 22 décembre 1887, c’est à dire les 4 nombres de la première ligne du carré : 22 12 18 87 …..
Les formules pour le fabriquer :
| a | b | c | d |
| d+m+n | c-m-n | b-m+n | a+m-n |
| b-m | a+m | d+m | c-m |
| c-n | d+n | a-n | b+n |
|
|
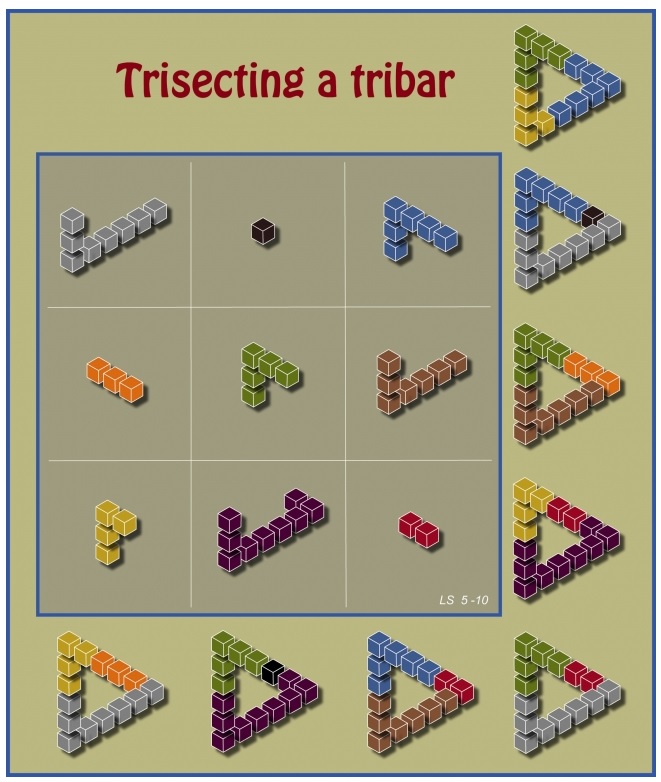
VI°/ Des carrés magiques géométriques :
On peut aussi utiliser des figures géométriques à la place des nombres.
 |
 |
 |
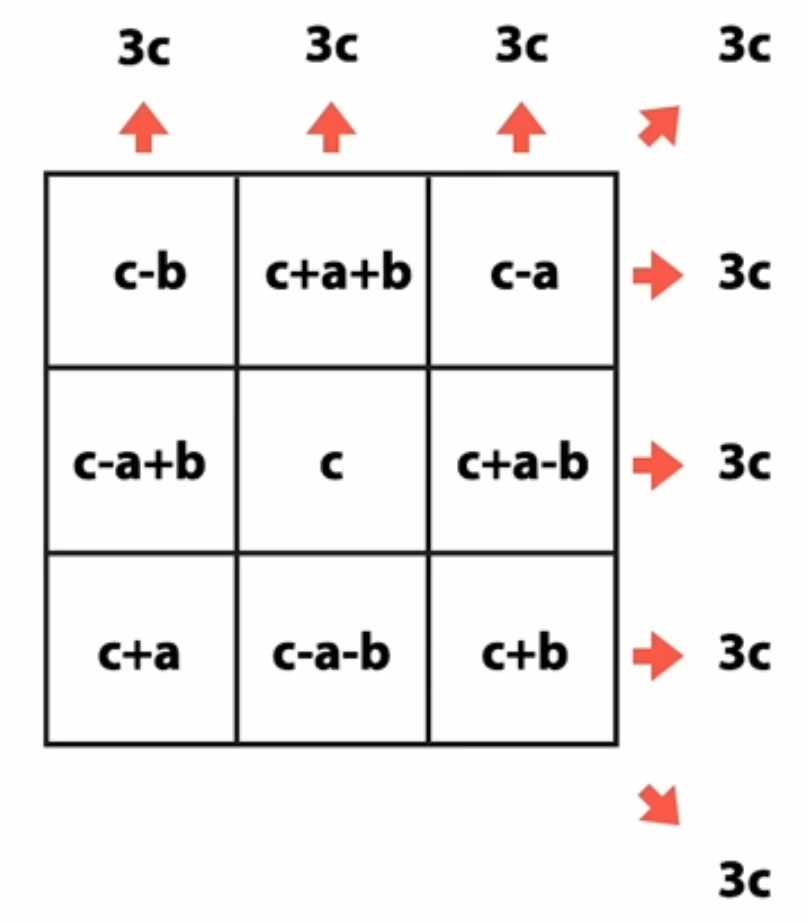
| Utilisons ses formules basiques. |
Remplaçons les 3 nombres de base par 3 figures géométriques. Chacune des cases du carré sera alors la composante des figures de base. |
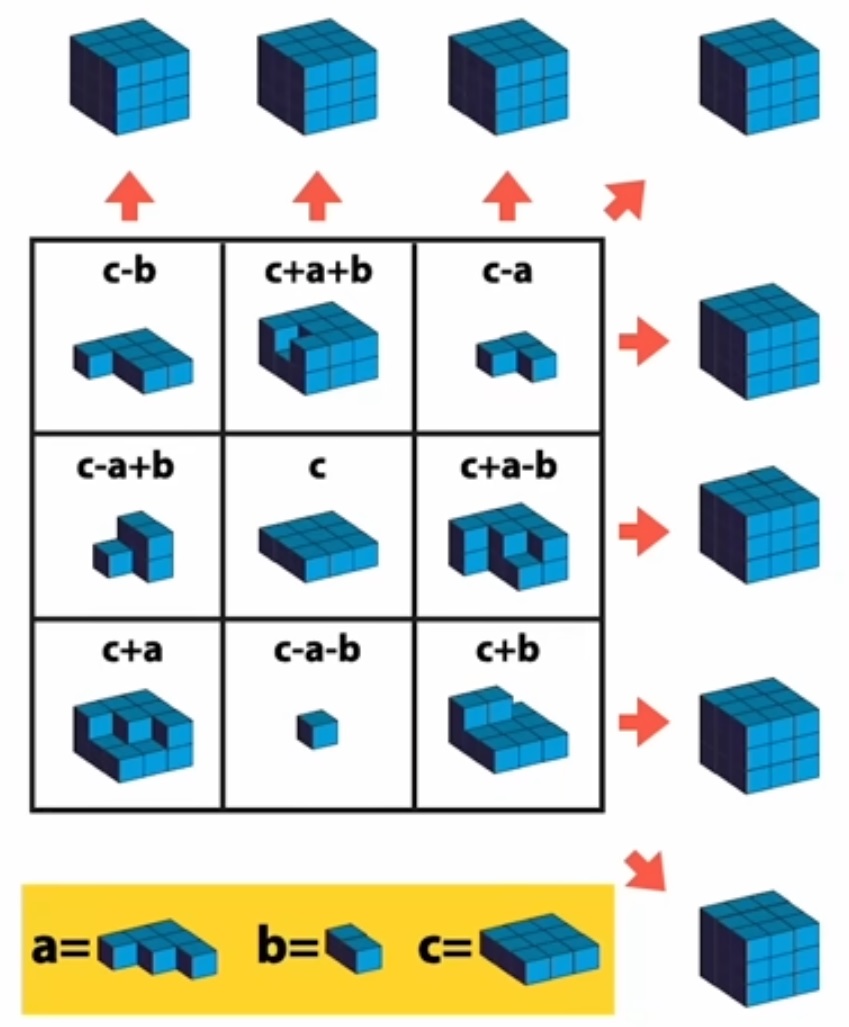
On peut aussi utiliser des modèles en 3D. |
 |
 |
 |
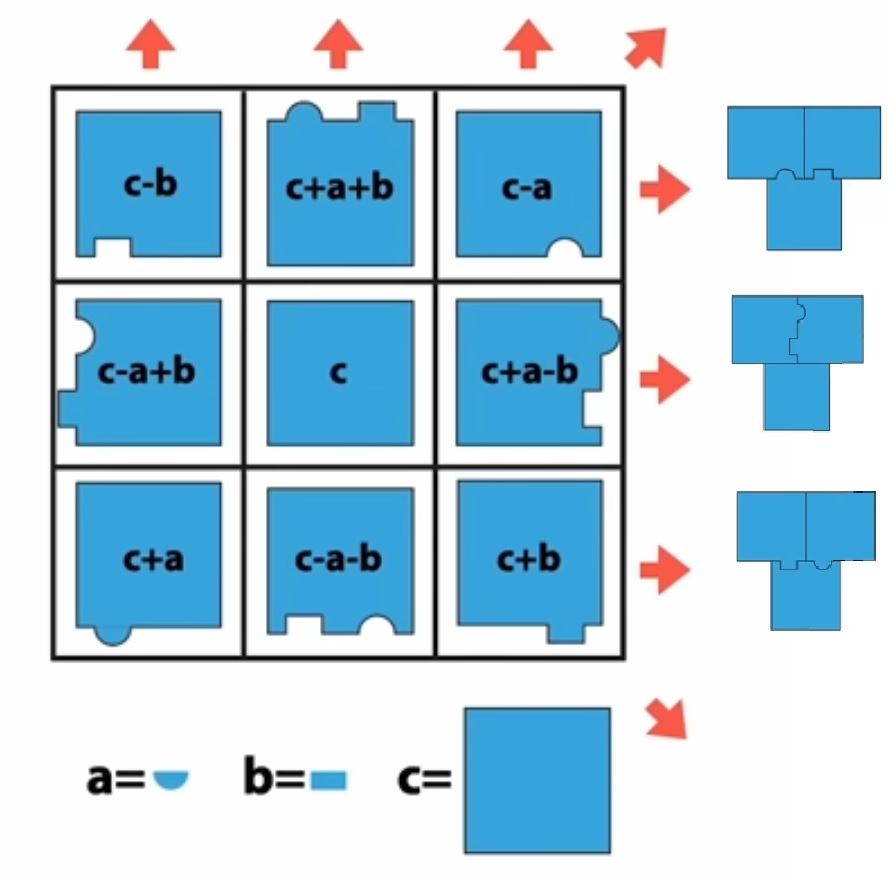
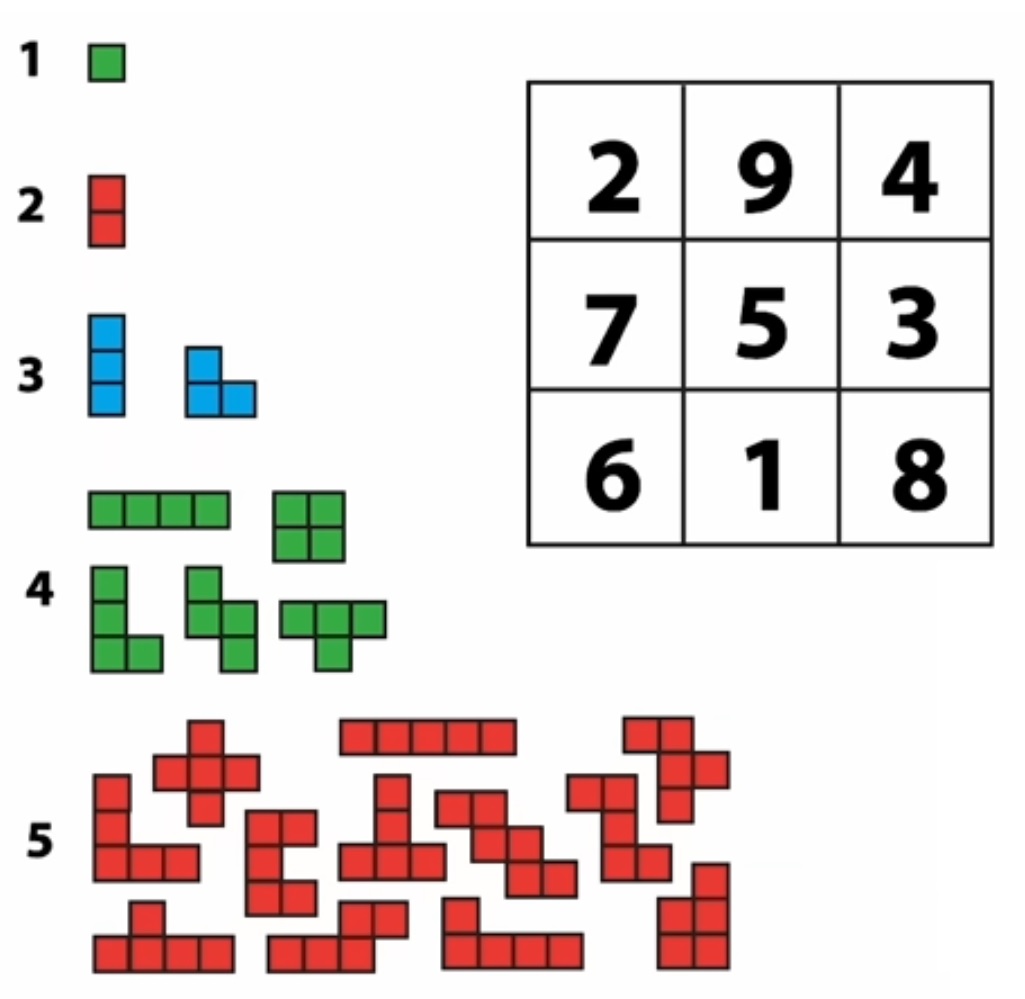
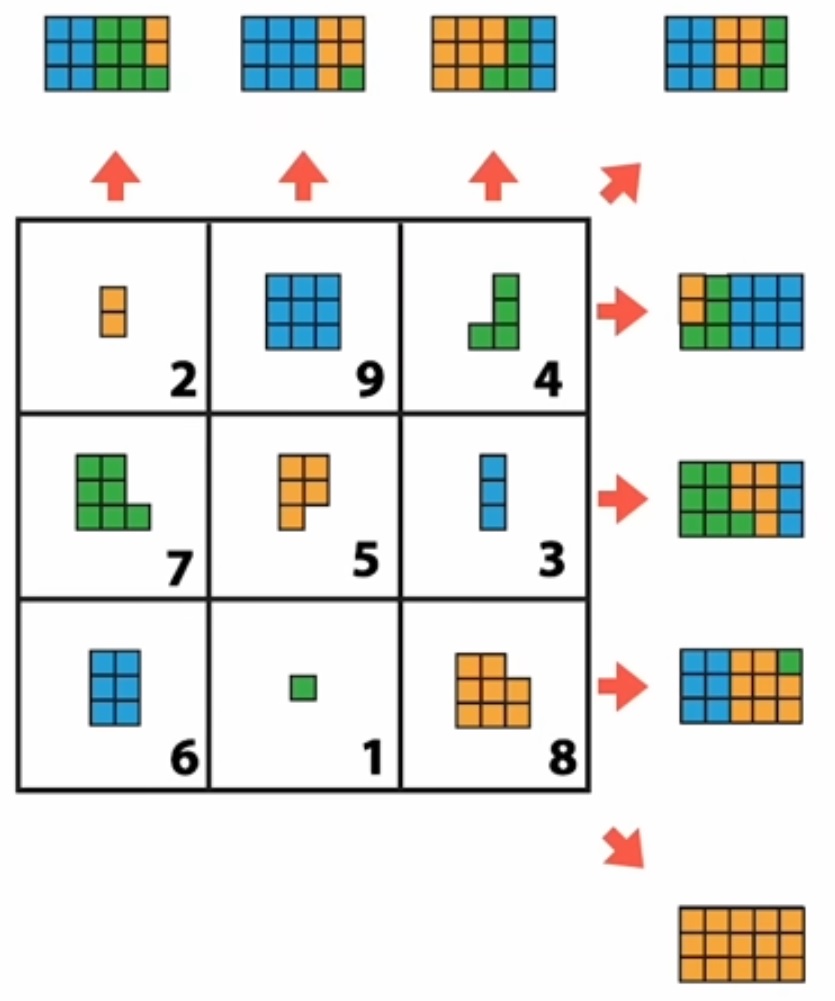
| Pour des formes un peu plus originales, utilisons de nouveau un carré magique de base. Pour chaque nombre, associons le même nombre de carreau en les assemblant de toutes les façons possibles, façon tangram. |
Si pour les nombres 1 et 2 il n’y a pas qu’une seule possibilité, le choix est plus vaste pour les autres. Voici une possibilité. |
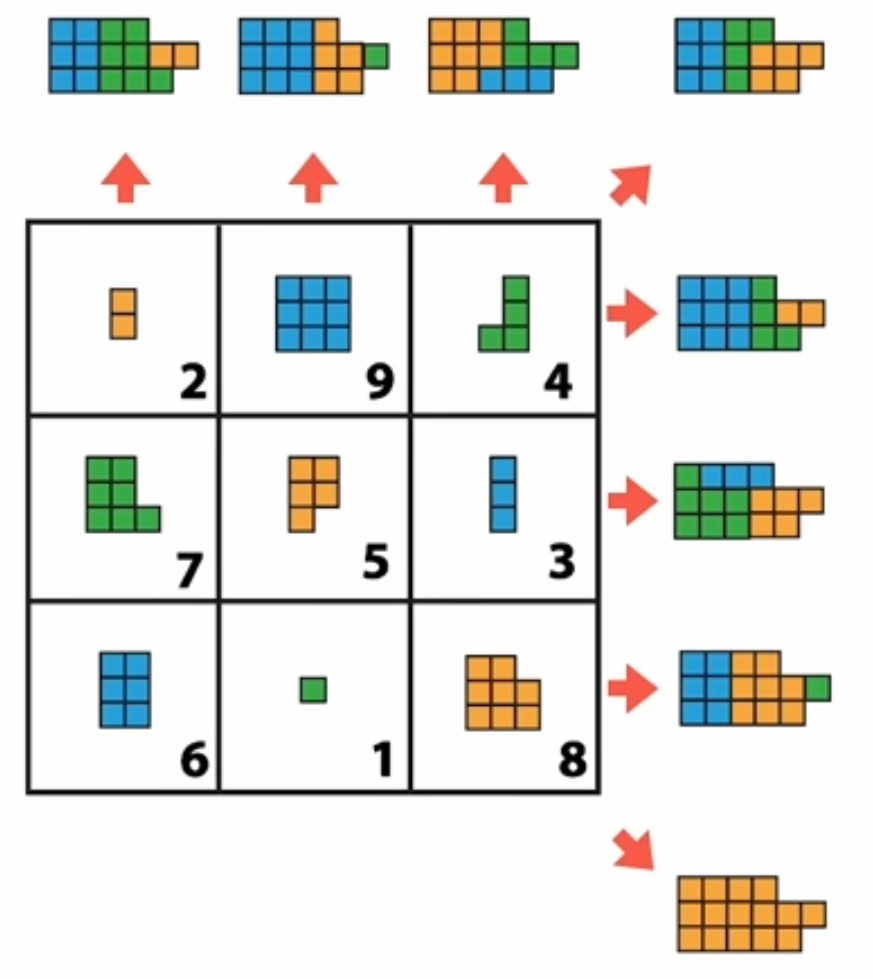
En voici une autre avec les mêmes pièces. |
Un site incroyable sur les carrés magiques géométriques :
Il existe d’autres carré magique géométrique, basés sur la surface. Un carré magique de surface est une sorte de carré magique où les nombres représentent les surfaces des sections colorées dans lesquelles ils apparaissent. Ce dessin de William Walkington s’inspire des techniques de construction de Walter Trump .
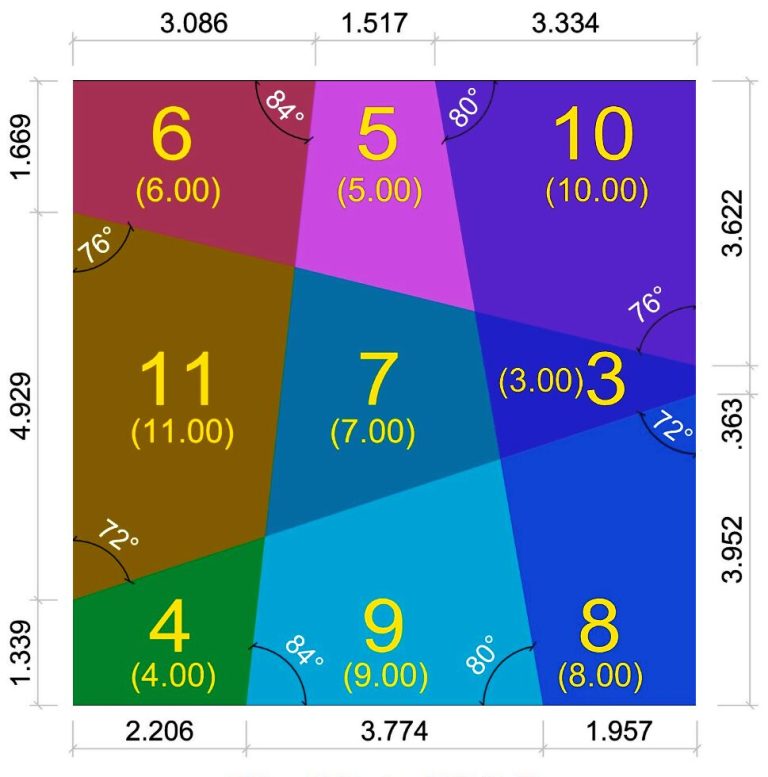
VII°/ Des carrés magiques circulaires :
|
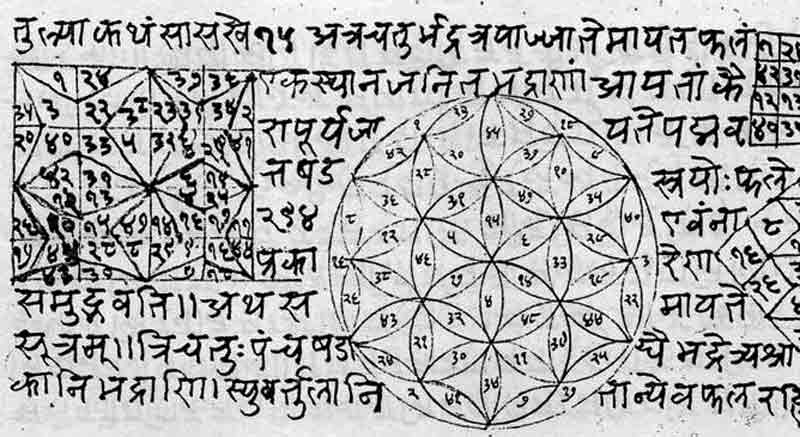
Le mathématicien indien Nārāyaṇa (1356) est à l’origine du « Lotus inscrit » (Padma Vrtta). |
un diagramme magique construit avec les nombres du rectangle magique 12×4), dans lequel chaque groupe de 12 nombres a la même somme 294. |
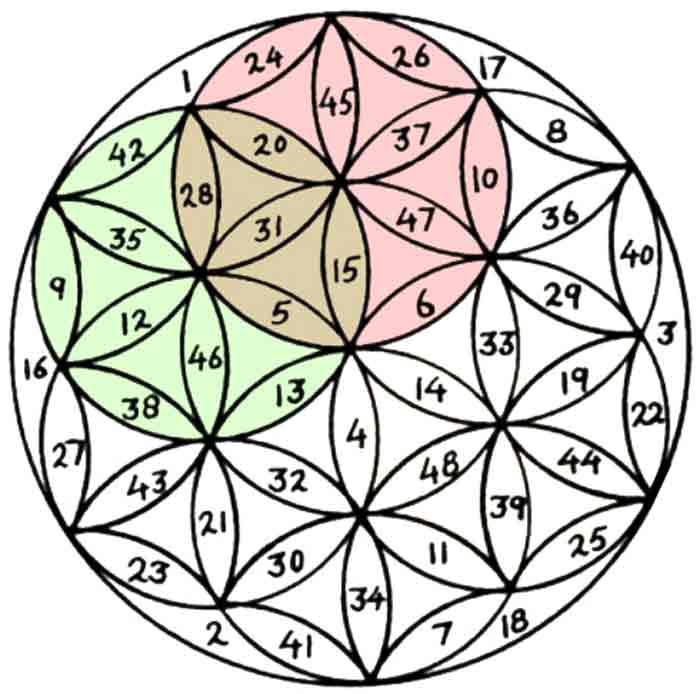
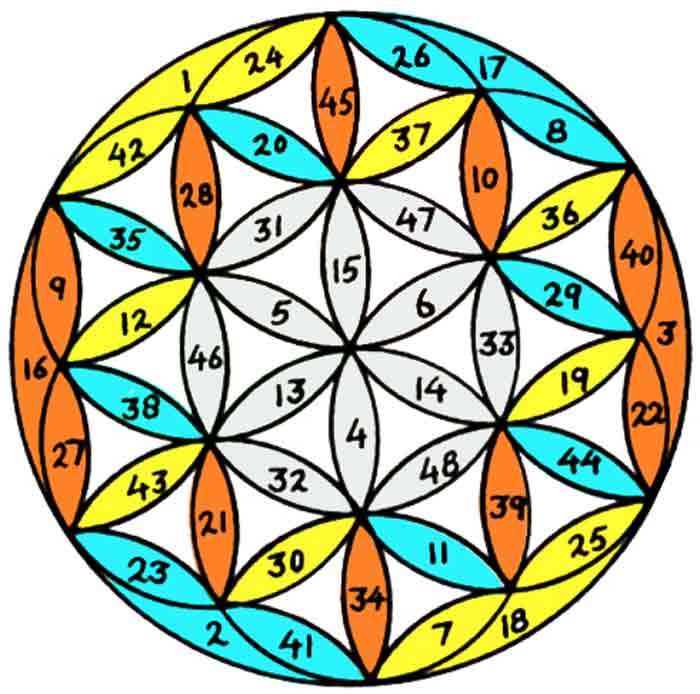
|
Chaque groupe de 12 nombres a la même somme 294. |
Le « Lotus inscrit » peut se transformer en un captivant mandala fractal. |
Conclure par un dessin : le « Lotus inscrit » peut se transformer en un captivant mandala fractal.
VIII°/ Les formules :
1°/ Carré magique 3×3 : il faut choisir 3 nombres.
| a-b | a+b+c | a-c |
| a+b-c | a | a-b+c |
| a+c | a-b-c | a+b |
2°/ Carré magique 4×4 : il faut choisir 6 nombres.
| a | b | c | d |
| d+m+n | c-m-n | b-m+n | a+m-n |
| b-m | a+m | d+m | c-m |
| c-n | d+n | a-n | b+n |
3°/ Carré magique 5×5 : il faut choisir 9 nombres.
|
h+d−i |
a |
e+f−i |
b |
g+c−i |
|
e |
b+g−i |
c+d−i |
a+h−i |
f |
|
a+c−i |
f+h−i |
i |
e+g−i |
b+d−i |
|
g |
e+d−i |
a+b−i |
f+c−i |
h |
|
b+f−i |
c |
g+h−i |
d |
a+e−i |
IX°/ Carrés magiques et symétrie :
Lors de l’utilisation de caractères standard, les chiffres 0, 1 et 8 sont symétriques autour de l’axe horizontal, tandis que 6 et 9 sont interchangeables lorsqu’ils sont tournés de 180 degrés.
Avec ces chiffres, nous pouvons créer des carrés magiques qui maintiennent leur somme constante même lorsqu’ils sont retourné.
|
Somme magique = 96 + 11 + 89 + 68 = 264 |
Rotation de 180° : Somme magique = 18+ 99+ 86+ 61= 264 |
Il est intéressant de noter que lorsque ces nombres sont représentés sous forme d’écran LCD, nous pouvons également inclure le chiffre 2, qui ressemble à un 5 lorsqu’il est inversé. Cela permet de créer des carrés magiques avec des propriétés supplémentaires liées à la symétrie 2D et 3D, qu’ils soient inversés ou en miroir.