Un nombre est dit premier, s’il admet exactement 2 diviseurs distincts (lui-même et l’unité). 1 n’est donc pas premier.
A°/ Crible d’Ératosthène :
B°/ Crible géométrique :
C°/ Les nombres premiers particuliers :
D°/ Visualisation des nombres premiers :
A°/ Crible d’Ératosthène :
On désigne sous le nom de crible d’Ératosthène une méthode de recherche des nombres premiers plus petits qu’un entier naturel n donné.
Pour ceci, on écrit la liste de tous les nombres jusqu’à n.
– On élimine 1.
– On souligne 2 et on élimine tous les multiples de 2.
– Puis on fait de même avec 3.
– On choisit alors le plus petit nombre non souligné et non éliminé ici 5, et on élimine tous ses multiples.
– On réitère le procédé jusqu’à la partie entière de la racine de n.
Les nombres non éliminés sont les nombres premiers jusqu’à n.
Les nombres premiers plus petits que 100 sont donc :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Les nombres premiers sont connus depuis l’Antiquité mais en dépit de la fascination qu’ils exercent il n’a pas encore été possible de percer leur mystère, c’est-à-dire de savoir s’il existe ou non, une loi de leur formation.
Euclide démontrait très simplement dans les Eléments (livre IX, 20) que la suite des nombres premiers était illimitée, et donc leur nombre infini.
En 1971, Tuckermann calcula un nombre premier avec 6 002 chiffres : 219937 – 1.
Le plus long nombre premier, comptant plus de 7 millions de chiffres, a été découvert grâce au programme du GIMPS (Great Internet Mersenne Prime Search) qui utilise des ordinateurs en réseau pour effectuer les monstrueux calculs nécessaires à la découverte de tels objets mathématiques
B°/ Crible géométrique :
Ci-dessous une parabole et son axe de symétrie horizontal.
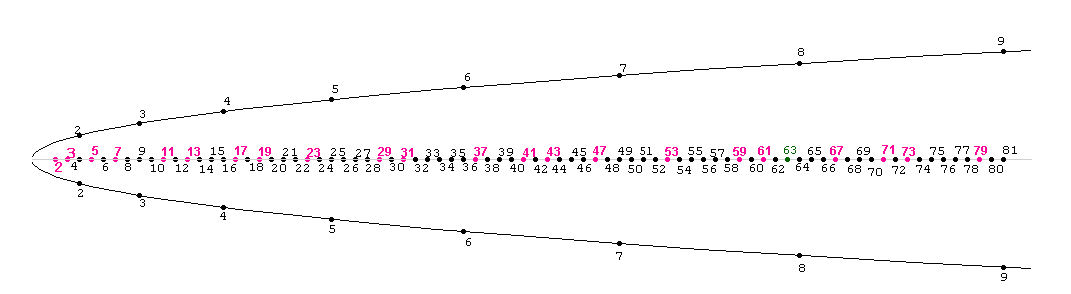
Le produit de deux nombres entiers notés sur chaque branche de la courbe, se lit directement à l’intersection du segment vert et de l’axe de la parabole (la ligne droite médiane qui est l’axe de symétrie de la parabole).
En plaçant des points de coordonnées entières sur chaque branche de la parabole et en les reliant systématiquement par des segments coupant l’axe de symétrie, on obtient les produits de ces deux entiers.
Les points (à abscisse entière) de l’axe par lesquels les segments ne passent pas sont donc des nombres premiers (2).
Ainsi nous obtenons un crible géométrique très simple pour trouver les nombres premiers.
Cette idée simple et géniale nous vient des mathématiciens russes Yuri Matiiassevitch et Boris Stechkin.
Cliquez sur crible géométrique.fig pour voie l’animation :
C°/ Les nombres premiers particuliers :
1/ Un nombre premier particulier : 2357223335555577777772357
Il est composé de 2357 puis de deux 2, puis de trois 3, puis de cinq 5, puis de sept 7 et enfin il finit de nouveau par 2357.
2/ Nombres premiers jumeaux : ils sont séparés par 2 unités. Les trois plus petits couples de nombres premiers jumeaux sont (3, 5), (5, 7) et (11, 13).
Le plus grand connu est 2 996 863 034 895 × 221 290 000 ± 1. Les deux nombres possèdent 388 342 chiffres (septembre 2016).
On soupçonne qu’il existe une infinité de ces couples, mais personne n’a pu le prouver à ce jour.
3/ Nombres premiers cousins : ils sont séparés par 4 unités.
4/ Nombres premiers sexys : ils sont séparés par 6 unités.
5/ Nombres premiers de Pythagore : Les nombres premiers de la forme 4n + 1, où n est un entier naturel. Par exemple, le nombre premier 5 est de Pythagore.
6/ Nombres premiers de Mersenne: Les nombres premiers de la forme Mp = 2p – 1 où p est alors nécessairement aussi premier.
7/ Nombres premiers de Fermat : Les nombres premiers de la forme Fn = 22n où n est un entier naturel. Petit soucis de définition, seuls les 5 premiers nombres de Fermat sont premiers ….
6/ Nombres premiers de Sophie Germain : Un nombre premier G est un nombre premier de Sophie Germain si 2G + 1 est aussi un nombre premier, appelé nombre premier sûr. Les dix premiers nombres premiers de Sophie Germain sont 2, 3, 5, 11, 23, 29, 41, 53, 83, 89.
8/ Nombres premiers rep-units : S’écrit seulement avec des 1. Par exemple, 1, 11 que l’on notera (1)2.
Jusqu’à présent, on ne connait que 5 repunits premiers : 11, (1)19, (1)23, (1)317 (Williams – 1978) et (1)1031. (Williams et Dubner – 1985). Pour tous les autres n inférieurs à 30 000, il n’y a pas de repunits premiers. Après, les calculs deviennent un brin compliqués…
Les repunits probablement premiers sont (1)49 081 (Dubner – 1999), (1)86 453 (Baxter – 2000), (1)109 297 (Dubner – 2007) et (1)270 343 (Voznyy – 2007). Et on s’arrête là, c’est déjà pas mal !
9/ Nombres premiers palindromes : Qui se lisent dans les deux sens.
Nombre à 1 seul chiffre : 2, 3, 5, 7.
En considérant que 1 est un nombre premier :
Nombre à 2 seul chiffres : il n’y a que 11, les autres seront des multiples de 11.
Nombre à 3 seul chiffres : 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929.
Nombre à 4 seul chiffres : il n’y a pas un seul nombre premier palindrome !
Nombre à 5 seul chiffres : il y en a 93.
En fait, on peut facilement voir que tout nombre palindrome de longueur paire est divisible par 11, car il vérifie le critère de divisibilité par 11 !
Pour les curiosités des nombres premiers palindromes, on a :
* 1 023 456 987 896 543 201, le plus petit palindrome premier qui contient tous les chiffres de 0 à 9
* 1(0)749997426247(0)749991, ((0)74999, c’est une suite de 74999 zéros) est le plus grand palindrome premier prouvé comme tel ! (Joblin – 2005 – 150 007 décimales)
* 1(0)56514661664(0)56511 est un nombre premier triplement palindrome : il est premier, il est palindrome, et son nombre de chiffres, 11311, est également palindrome et premier !
10/ Les nombres premiers raccourcissables : Le nombre 35 768 631 264 6216 567 629 137 est le plus long nombre premier connu qui reste premier si on lui enlève son premier chiffre. Un nombre premier de ce type est appelé « raccourcissable à gauche ». 73939133 et 1979339333 sont « raccourcissable à droite et 11311, 71317, 93739, 1335331, 3315133 et 9375739 sont « raccourcissable à gauche » et à droite !!!
11/ Méchant Premier :
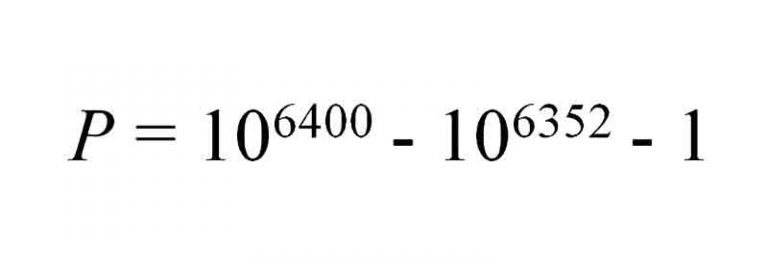
Le nombre premier P contient 6400 chiffres composés de 9 à l’exception d’un seul 8 caché dans le paquet de chiffres :
999999999999999999999999999999999999999999999999999899999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
12/ Le plus grand :
\Large 2^{136279841}-1Découvert le 12 octobre 2024, c’est le plus grand nombre premier connu. Ce nombre a 41 024 320 chiffres… C’est (comme toujours) un nombre premier de Mersenne.
Il a fallu près de 6 ans au logiciel GIMPS pour le trouver après le précédent record.
D°/ Visualisation des nombres premiers :
|
Chaque nombre est décomposé en ses multiples, par exemple : 12 = 3 x 4 boules. Les nombres premiers sont eux représentés sous forme de cercle. |
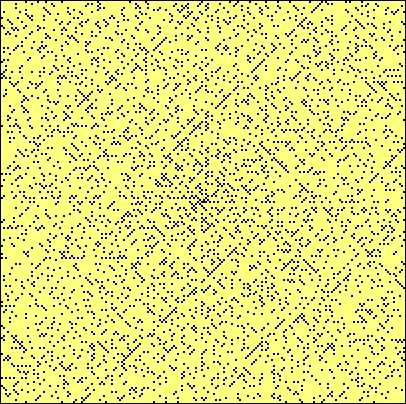
Mais on peut trouver d’autre façon de ranger les nombres premiers.
 |
 |
 |
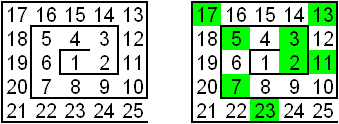
| L’anecdote raconte qu’en 1963, le mathématicien Stanislaw Marcin Ulam fut contraint d’écouter un exposé très long et très ennuyeux. Il commença alors à écrire les entiers sous forme d’une spirale. Il entoura ensuite les nombres premiers… | Au premier abord, il n’y a rien à voir, mais si on pousse le dessin plus loin, on trouve cette spirale d’Ulam (ou « horloge d’Ulam ») (200×200) | Et si, au lieu de prendre une spirale carrée, on prend une vraie spirale ? Une spirale d’Archimède, par exemple. En s’arrangeant pour que tous les carrés parfait soient alignés, et en mettant le 0 au milieu, on trouve la spirale de Sacks (1994) |