L’idéal pour une feuille, serait que son format ne change pas lorsqu’on la plie en deux ou que l’on fait un agrandissement ou une réduction avec une photocopieuse.
Pour cela le rapport Longueur sur largeur doit être constant d’un format à l’autre, et pour que l’on puisse plier parfaitement une feuille en deux.
Quel doit être ce rapport ?
Dans le tableau excel suivant, on se rend compte que si on prend une Longueur 2 fois plus grande que la largeur, le format suivant est un carré de rapport 1, puis le suivant un rectangle de rapport 2 et ainsi de suite. Avec les images qui suivent où la Longueur de départ est le double de la largeur, le burro Catalan grossit puis revient aux bonnes proportions au fil des réductions.




Utilisez ce fichier Excel pour fabriquer vos propres formats : Format A4. http://trabucaire.free.fr/wp-content/uploads/2020/07/Racine-carree-compte-goutte.xlsx
Format B4 où le rapport L/l n’est constant.
Pour que les images ne se déforment pas, quel doit être le bon rapport ?
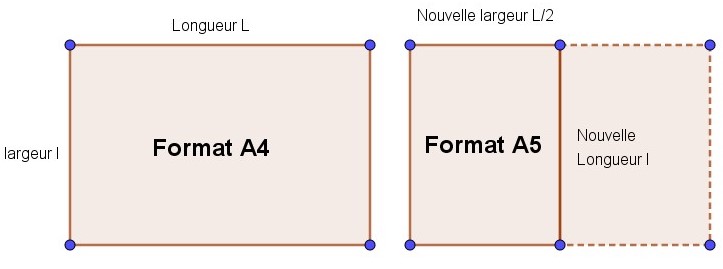 |
Soit L la longueur d’une feuille et l sa largeur.
Lorsqu’on la coupe en deux, la largeur de la nouvelle feuille est la moitié de la Longueur précédente, et sa longueur est maintenant l. Pour avoir la même forme il faut que le rapport des deux mesures soit identique : \frac{Ancienne \ Longueur \ L}{Ancienne \ largeur \ l} = \frac{Nouvelle\ Longueur \ l}{Nouvelle\ largeur \ L/2} \Rightarrow \frac{L^{2}}{l^{2}}=2 \Rightarrow \frac{L}{l} = \sqrt{2}\approx 1,414 |
La première référence au rapport \sqrt{2} ce trouve dans une lettre écrite le 25 octobre 1786 par le professeur de physique Georg Christoph Lichtenberg (Université de Göttingen, Allemagne, 1742-1799) à Johann Beckmann. Il se trouve que le papier sur lequel était écrit cette lettre respecté justement ce rapport de \sqrt{2} entre la Longueur et la largeur.
L’Organisation Internationale de Normalisation (ISO) constitua en 1947 le Comité Technique ISO/TC 6 « papier » qui chargea un de ses sous-comités d’étudier les dimensions internationales des papiers et des cartons. La recommandation fut demandée d’envisager la normalisation des formats.
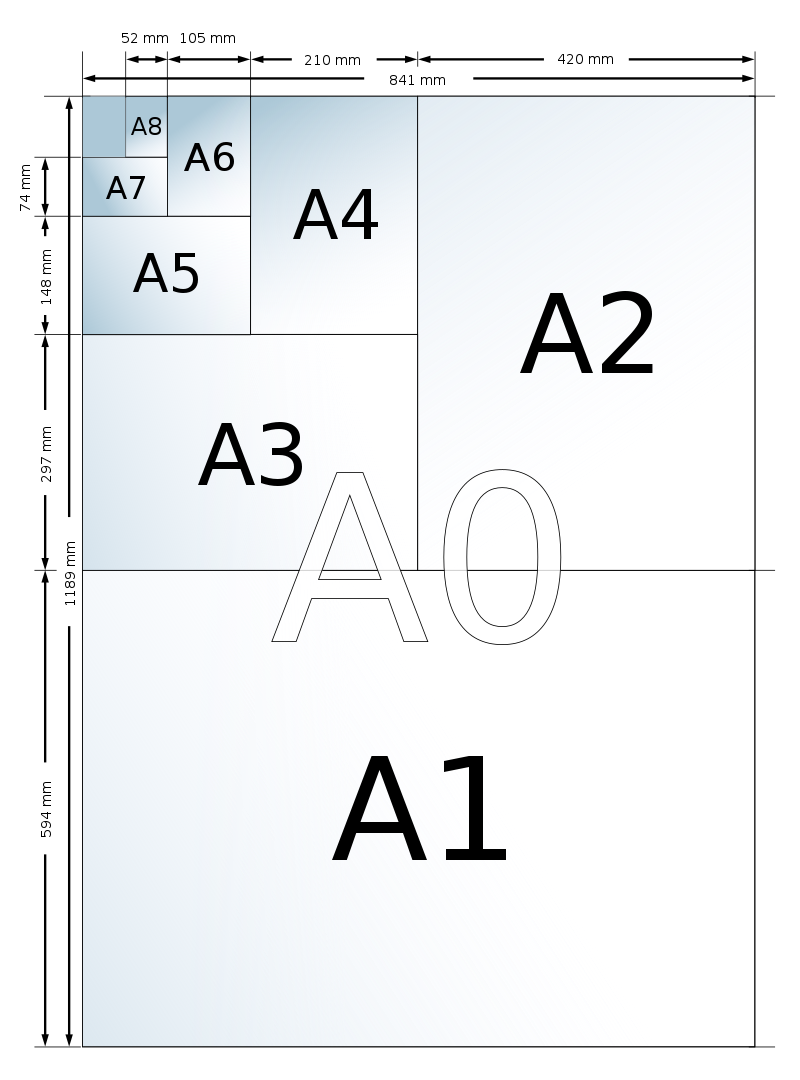
Comme nous l’avons vu ci-dessus, lorsqu’on plie en deux une feuille A4, le format reste identique : le rapport longueur sur largeur de la feuille reste constant. C’est très pratique. Ainsi nous passons du format A3 au format A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant également en deux une feuille A4.
Le format de départ A0 est défini comme ayant une surface mesurant 1 m². Quelles seront ces dimensions ?
| Format | Longueur en cm | largeur en cm | Rapport | Aire en m² | Poids en g |
| A0 | 118,9 | 84,1 | \frac{118,9}{84,1} =1,413794 | 1 | 80 |
| A1 | 84,1 | 59,5 | \frac{84,1}{59,5} =1,413445 | 1/2 | 40 |
| A2 | 59,5 | 42 | \frac{59,5}{42} =1,416667 | 1/4 | 20 |
| A3 | 42 | 29,7 | \frac{42}{29,7} =1,414141 | 1/8 | 10 |
| A4 | 29,7 | 21 | \frac{29,7}{21} =1,414286 | 1/16 | 5 |
| A5 | 21 | 14,8 | \frac{21}{14,8} =1,418919 | 1/32 | 2,5 |
Ainsi le rapport Longueur/Largeur est identique pour toutes les feuilles et chacune contient exactement deux feuilles du format immédiatement inférieur.
Notons qu’avec du papier 80g/m², une feuille A4 d’aire 1/16 m² pèse 5g. Nous pouvons donc placer 3 feuilles dans une enveloppe et mettre un timbre normal sur l’enveloppe (moins de 20g).