I°/ Utilisation :
A°/ En comptant les points :
B°/ En comptant les côtés des quadrillages :
C°/ En comptant les carrés des quadrillages :
II°/ Démonstration :
A°/ Démonstration dans un rectangle :
B°/ Démonstration dans un triangle rectangle :
C°/ Démonstration dans un triangle quelconque :
D°/ Démonstration dans un polygone quelconque :
III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky
IV°/ Le théorème de Wallace-Bolyai-Gerwien :
V°/ La formule de Euler : S – A + F = 2
Le théorème de Pick permet de calculer l’aire de n’importe quel polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.
I°/ Utilisation :
Dessinons un polygone sur une feuille quadrillée. Si les sommets du polygone sont sur les nœuds du quadrillage et si ce polygone n’est pas croisé, alors on peut calculer très simplement son aire, c’est à dire la mesure de sa surface.
A°/ En comptant les points : Aire = e/2 + i – 1
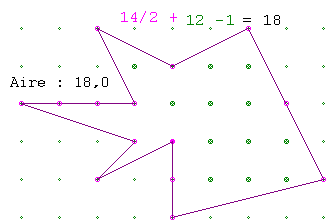 |
Soit e le nombre de points du réseau qui touchent les côtés, sommets compris (ici 14 points roses). Soit i le nombre de points qui sont à l’intérieur de la figure (ici 12 points verts). Aire = e/2 + i – 1 = 14/2 + 12 – 1 = 18 |
B°/ En comptant les côtés des quadrillages : Aire = i/2 + (c+t)/4
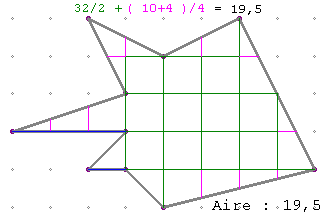 |
Soit i le nombre de côtés entièrement intérieurs à la figure (32 côtés verts). Soit c le nombre de côtés coupés intérieurs à la figure (10 côtés roses). Soit t le nombre de côtés de carrés sur la frontière de la figure (4 côtés bleus). Aire = i/2 + (c + t)/4= 32/2 + (10 + 4)/4 = 16 + 3,5 = 19,5 |
C°/ En comptant les carrés des quadrillages : Aire = e + c/2
 |
Soit e le nombre de mailles entièrement à l’intérieur de la figure (7 ronds verts). Soit c le nombre de mailles coupées par la frontière de la figure (11 ronds roses). Aire = e + c/2= 7 + 11/2 = 12,5 |
Entrainez-vous avec ce polygone :
Ou alors :
II°/ Démonstration :
Si : i = le nombre de points à l’intérieur du polygone.
b = le nombre de points sur les bords (côtés) du polygone.
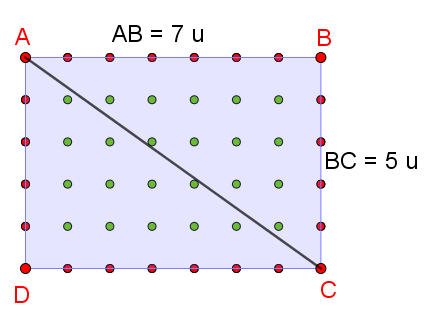
A°/ Démonstration dans un rectangle :
1°/ Par le calcul : Soit un rectangle ABCD de longueur AB et de largeur BC.
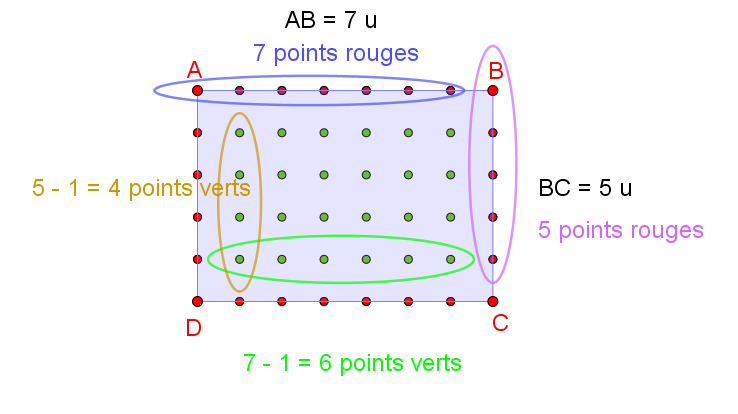 |
Points verts : i = (AB – 1)(BC – 1)
Points rouges : b = 2x(AB + BC) Donc : Aire_{polygone}=i+ \frac{b}{2}-1= ABxBC – AB – BC + 1 + AB + BC – 1 = ABxBC Donc la formule de Pick nous donne bien la formule générale de l’aire d’un rectangle : Longueur fois largeur. Dans l’exemple : Aire_{rectangle}=i+\frac{b}{2}-1=24+\frac{24}{2}-1=24+12-1=35 u^{2} Aire_{rectangle}=L \times l =7 \times 5=35 u2La formule de Pick est vérifiée pour les rectangles. |
2°/ Par la géométrie : Soit un rectangle ABCD de longueur AB et de largeur BC.
Décalons le quadrillage d’un demi carreau pour intégrer les points verts dans des carrés de même surface que les carrés représentés par 4 points de couleurs.
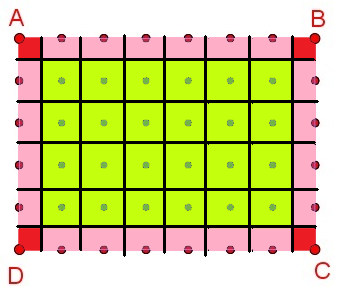 |
Nombre de carrés verts contenant les points verts : (AB – 1)(BC – 1) = ABxBC –AB – BC + 1
Nombre de rectangles roses contenant les points rouges : 2 x [(AB – 1) + (BC – 1)] = 2AB + 2BC – 4 Nombre de carrés rouges contenant les points rouges : 4 Donc : Points verts : i = (AB – 1)(BC – 1) = ABxBC –AB – BC + 1 Points rouges : b = 2AB + 2BC – 4 + 4 = 2AB + 2BC Aire_{rectangle}=i+ \frac{b}{2}-1 = ABxBC –AB – BC + 1 + AB + BC -1 = ABxBC = Longueur fois largeur. |
B°/ Démonstration dans un triangle rectangle :
Un triangle rectangle est la moitié d’un rectangle. Donc :
 |
Points verts du triangle : it
Points rouges des côtés perpendiculaires du triangle : bt Points rouges de l’hypoténuse du triangle sans les extrémités : h Points verts du rectangle (ceux des 2 triangles plus ceux présents sur l’hypoténuse) : ir = 2 it + h Points rouges du rectangle (ceux des 2 triangles, sans les 2 hypoténuses, moins 2 sommets comptés 2 fois) : br = 2 bt – 2h – 2 Aire_{rectangle}=i+ \frac{b}{2}-1= 2 it + h + bt – h – 1 – 1 = 2it + bt – 2 = 2\times (i_{t}+\frac{b_{t}}{2} -1) Aire_{rectangle}=2 \times Aire_{triangle} |
C°/ Démonstration dans un triangle quelconque :
On peut inscrire un triangle quelconque dans un rectangle. t1 = AED ; t2 = EBF; t3 = FCD et t = CDE
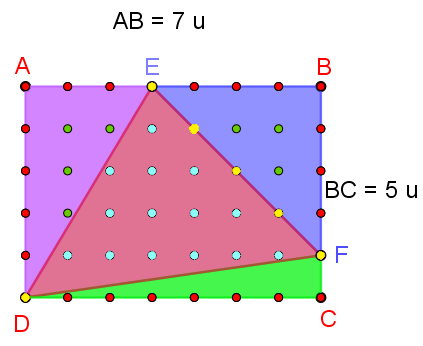 |
Points verts du rectangle ABCD (ceux des 4 triangles plus ceux présents sur les hypoténuses des 3 triangles rectangles) :
ir = it1 + h1 + it2 + h2 + it3 + h3 + it Points rouges du rectangle (ceux des 3 triangles t1, t2 et t3, sans leurs hypoténuses, moins 6 sommets comptés 2 fois pour chacun des 3 triangles) : br = bt1 – h1 + bt2 – h2 + bt3 – h3 – 6 De plus les points sur les bords du triangle CDE sont ceux présents sur les 3 hypoténuses : bt = h1 + h2 + h3 |
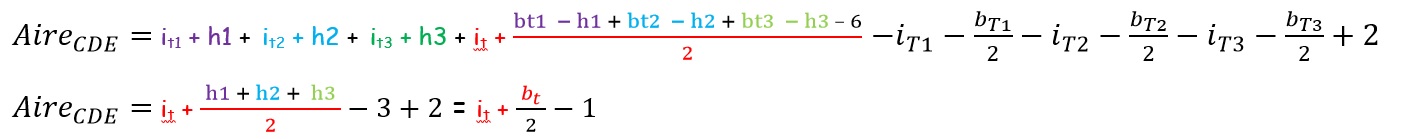
La formule de Pick est vérifiée pour les triangles quelconques.
Vérification sur l’exemple : Aire_{DEF}=i_{t}+ \frac{b_{t}}{2}-1 = 14 + \frac{6}{2}-1 = 16 unités d’aire
D°/ Démonstration dans un polygone quelconque :
Tout polygone peut être découpé en triangles, donc le théorème de Pick est à présent démontrer pour tout polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.
III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky
Ce théorème vaut par son titre amusant (à dire rapidement : mémère – pépère …), qui n’en est pas moins exact.
Il dit que si on peut découper un carré en triangles de même aires, alors il y a un nombre pair de triangle.
Autrement dit de façon Mathématiques mais mois rigolo, un carré n’admet pas d’équidissection impaire.
On peut généraliser ce théorème à tous les polygones.
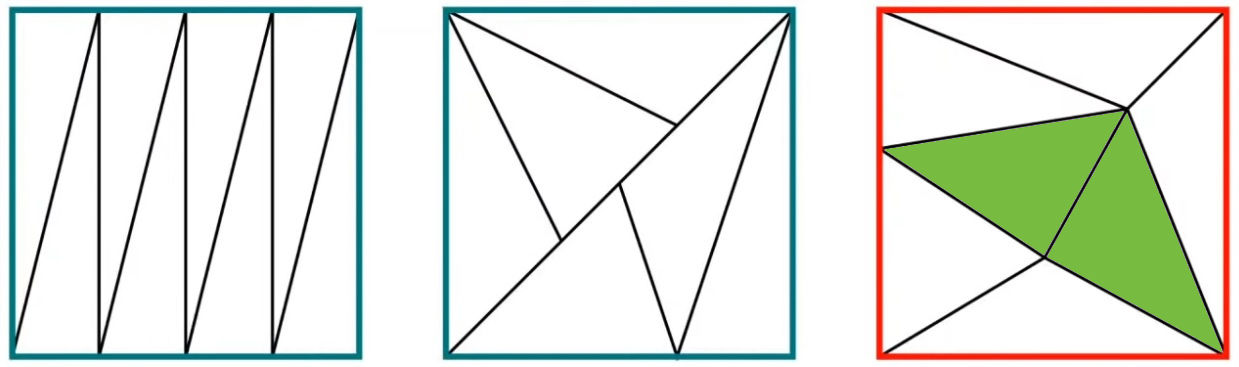
Il y a 8 triangles de même aire dans le premier carré et 6 de même aire dans le second. Par contre dans le troisième carré rouge, il y a 7 triangles dont les deux verts n’ont pas la même aire que les autres.
IV°/ Le théorème de Wallace-Bolyai-Gerwien : les formules des aires des polygones et des volumes des solides
Les matheux aiment le découpage : la preuve avec le théorème de Wallace-Bolyai-Gerwien et avec le théorème de Dehn !
Dans cette vidéo de El JJ nous verront comment retrouver les formules des aires des polygones et des volumes des solides par découpage, comment passer d’un polygone ou d’un polyèdre à un autre toujours par découpage et enfin nous découvrirons le 3ième problème de Hilbert.
V°/ La formule de Euler : S – A + F = 2
Pour les polygones, la formule d’Euler affirme que : S + R = A + 2 (S nombre de sommets, R nombre de régions délimitées par les arêtes et A nombre d’arêtes)
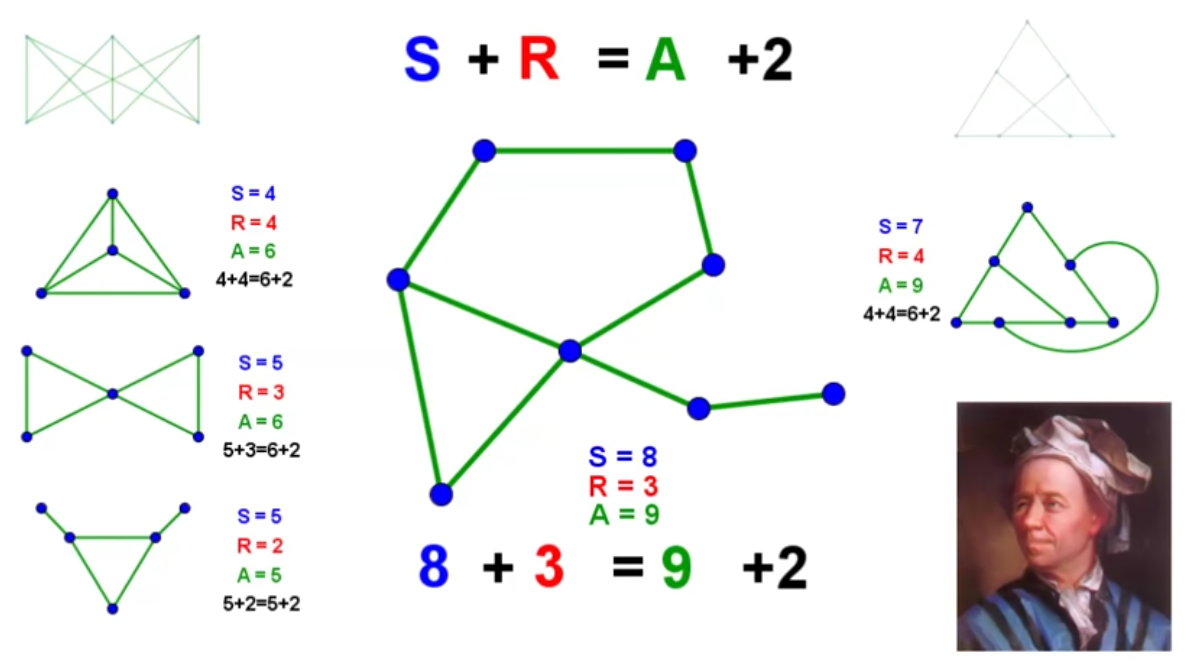
| 1 points | + 1 points = + 1 arêtes, donc pas de changement dans la formule. | + 1 région sans sommet = + 1 arête | ||
| Schéma | 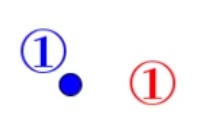 |
 |
 |
 |
| Sommet S | S = 1 | S + 1 = 1 + 1 = 2 | S + 4 = 5 | S = 5 |
| Régions R | R = 1 | R = 1 | R = 1 | R = 2 + 1 = 3 |
| Arêtes A | A = 0 | A + 1 = 0 + 1 = 1 | A + 4 | A = 5 + 1 = 6 |
| Formule d’Euler S + R = A + 2 |
1 + 1 = 0 + 2 = 2 | 2 + 1 = 1 + 2 = 3 S + 1 + R = A + 1 + 2 S + R = A + 2 |
5 + 1 = 4 + 2 = 6 S + 4 + R = A + 4 + 2 S + R = A + 2 |
5 + 3 = 6 + 2 = 8 S + R + 1 = A + 1 + 2 S + R = A + 2 |
Tour de magie :
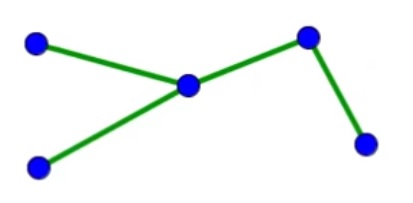
Cette formule permet de créer un petit tour de magie assez bluffant : gribouiller n’importe comment. La seule chose qui importe, c’est que le gribouillage soit en un seul morceau (connexe). Par exemple, vous pouvez faire un truc comme ça :
 |
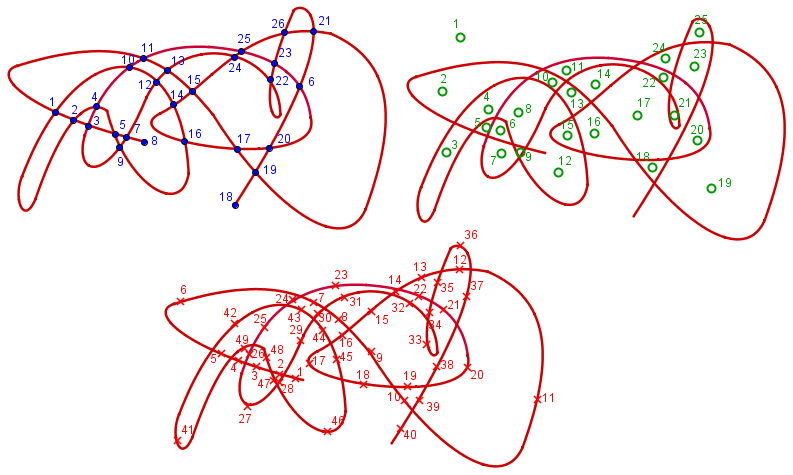 |
C’est maintenant qu’on va faire des maths ! Dans ce gribouillage, on peut repérer des « Sommets » S (les points d’intersection et les extrémités), des « Arrêtes » A (ce qui relie deux sommets) et des « Régions » R (les cellules, délimitées par des arrêtes. Au passage, l’extérieur de la figure est une face. On les appellent souvent Face F.). Comptez-les !
Moi, je compte S = 26 sommets (bleus), A = 49 arrêtes (rouges) et F = 25 faces (verts)
Attention, tour de magie qui n’impressionnera personne. Je suis sûr que si vous effectuez l’opération S – A + F = 26 – 49 + 25 = 2, vous trouverez toujours 2 !
La formule d’Euler pour les polyèdres convexes : S + F = A + 2 (S nombre de sommets, F nombre de faces et A nombre d’arêtes).

Une très belle vidéo :
| Vertices = sommets
Edges = arêtes Faces = faces Dans un polyèdre : Nombre de sommet – Nombre d’arêtes + Nombre de face = 2 S – A + F = 2 Ou en Anglais : V – E + F = 2 |