Un mathématicien ne croit pas se qu’il voit mais ce qu’il est capable de démontrer.
La démonstration mathématique est très rigoureuse mais vraiment basique. On part de certitudes et on fabrique des certitudes.
I°/ Les 5 postulats d’Euclide :
II°/ Ce qu’il est possible de construire :
III°/ Ce qu’il est impossible de construire :
1°/ La quadrature du cercle :
2°/ La trisection d’un angle :
3°/ Duplication du cube :
IV°/ La géométrie Shadok :
V°/ Des définitions originales :
I°/ Les 5 postulats d’Euclide :
La démonstration géométrique est issue de 5 principes de base que l’on doit au mathématicien Grec Euclide (-300 av JC) qui a rassemblé dans un ouvrage titanesque, les Éléments d’Euclide, l’ensemble des connaissances mathématiques de l’époque (consultable ici et téléchargeable).
 |
Chaque nouveau lemme ou théorème découle des précédents :
Liste de lemmes : En mathématiques, un lemme est un énoncé prouvé, mais jugé moins important qu’un théorème, qu’il sert généralement à établir une démonstration. Cette terminologie reste cependant subjective et relative à l’histoire d’une discipline. Liste de théorèmes : En mathématiques et en logique, un théorème (du grec théorêma, objet digne d’étude) est une assertion qui est démontrée, c’est-à-dire établie comme vraie à partir d’autres assertions déjà démontrées (théorèmes ou autres formes d’assertions) ou des assertions acceptées comme vraies, appelées axiomes. Un théorème se démontre dans un système déductif et est une conséquence logique d’un système d’axiomes. En ce sens, il se distingue d’une loi scientifique, obtenue par l’expérimentation. Liste des équations et formules : Ce sont les équations, formules, relations et autres identités, égalités ou inégalités. |
Le plus ancien extrait d’une copie des éléments d’Euclide
Voici les 5 postulats d’Euclide :
| 1- Un segment de droite peut être tracé en joignant deux points quelconques. |  |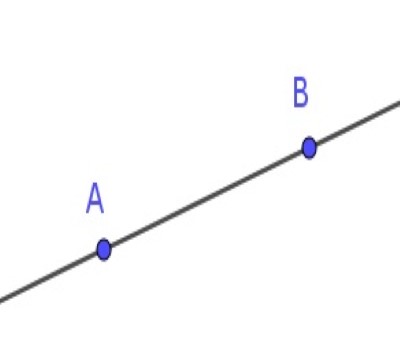
| 2- Un segment de droite peut être prolongé indéfiniment en une ligne droite. |  |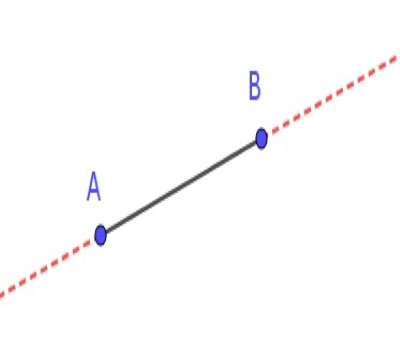
| 3- Étant donné un segment de droite quelconque, un cercle peut être tracé en prenant ce segment comme rayon et l’une de ses extrémités comme centre. |  |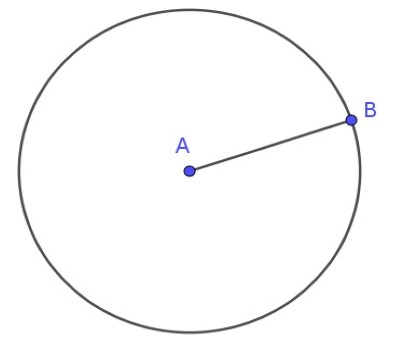
| 4- Tous les angles droits sont congruents c’est-à-dire qu’ils sont superposables. |  |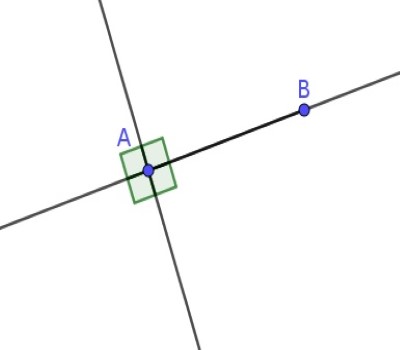
|
5- Si deux lignes droites sont sécantes avec une troisième de telle façon que la somme des angles intérieurs d’un côté est inférieure à deux angles droits, alors ces deux lignes sont forcément sécantes de ce côté (autrement dit : par un point extérieur à une droite donnée, ne passe qu’une unique droite qui lui est parallèle). C’est le plus contesté : on peut créer une géométrie non-euclidienne qui respecte les 4 premiers postulat sauf ce 5ième (Voir ici). |
 |
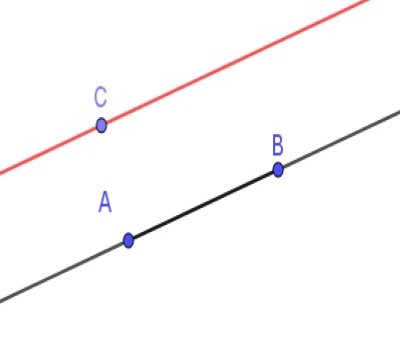Concrètement, on ne peut construire une figure qu’en utilisant une règle non graduée et un compas.
II°/ Ce qu’il est possible de construire :
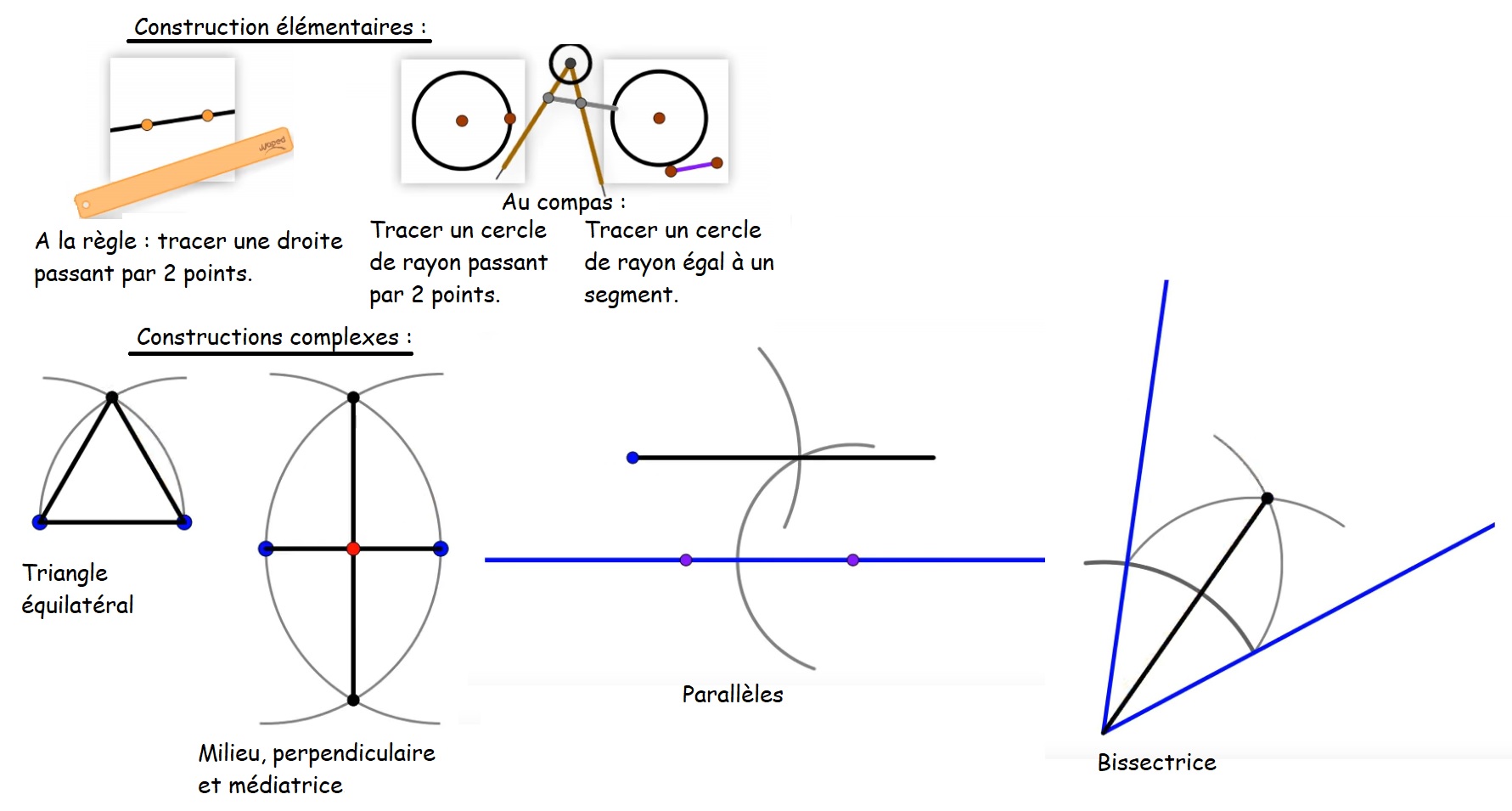Bien entendu la liste n’est pas exhaustive, et on peut construire beaucoup de figures à partir de ces éléments de base.
Il existe un excellent jeux qui permet de s’amuser avec les construction euclidienne : Euclidea.
Voici par exemple, 5 méthodes pour couper un segments en 5 parties égales.
Comment tracer un segment de \sqrt{3} ?
 |
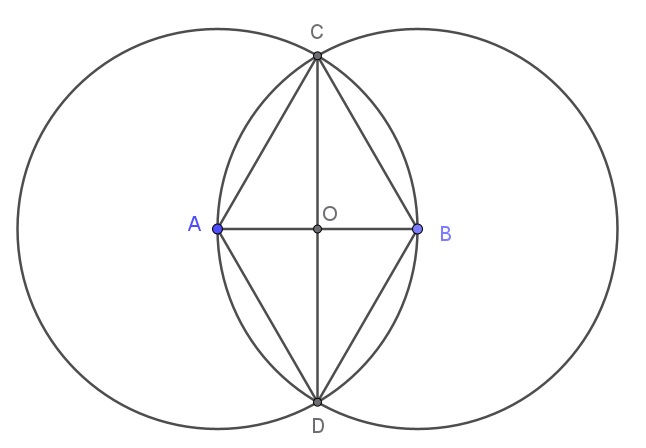Tracer 2 cercles de centre A et B, de même rayon et tels que chaque centre soit sur le cercle de l’autre. Prenons AB = 1 unité Dans le triangle AOC rectangle en O AC² = AO² + OC² donc : OC = \sqrt{AC^{2}-OC^{2}}=\sqrt{1^{2}-0,5^{2}}=\frac{\sqrt{3}}{2} Donc : CD = \sqrt{3} |
III°/ Ce qu’il est impossible de construire :
Pour résumer :
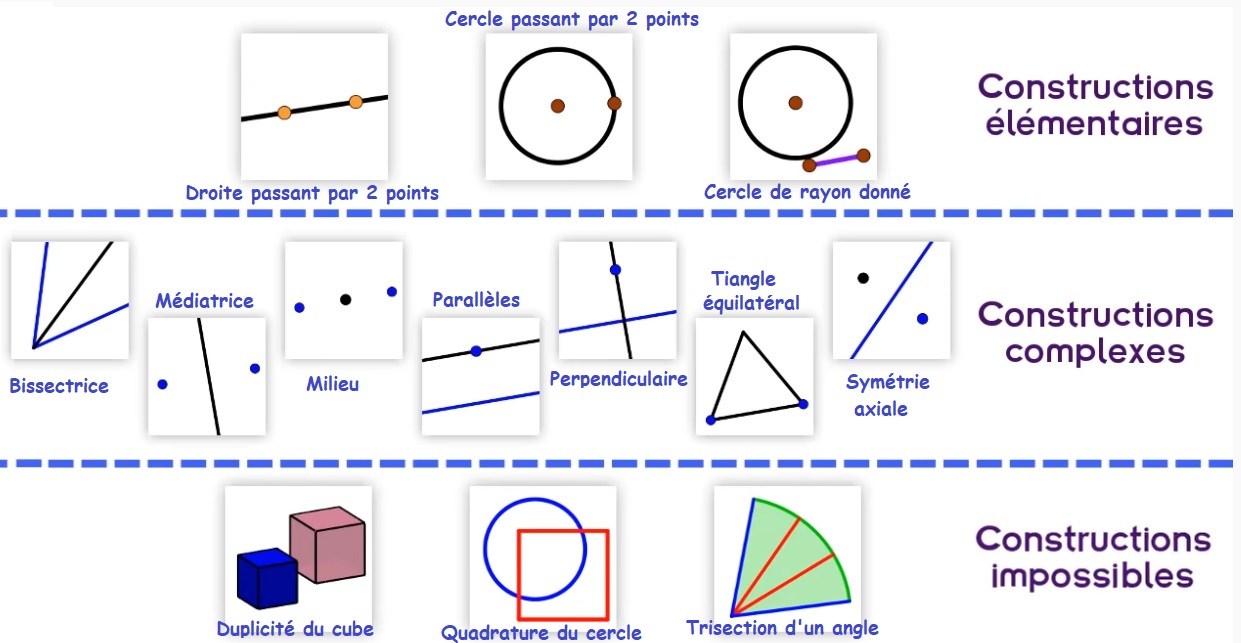
Pour savoir si une construction est possible, il suffit de savoir quelle est l’équation que l’on doit résoudre pour construire un point. A la règle et au compas, on ne peut fabriquer que les points d’intersections de 2 droites, d’une droite et d’un cercle et de 2 cercles.
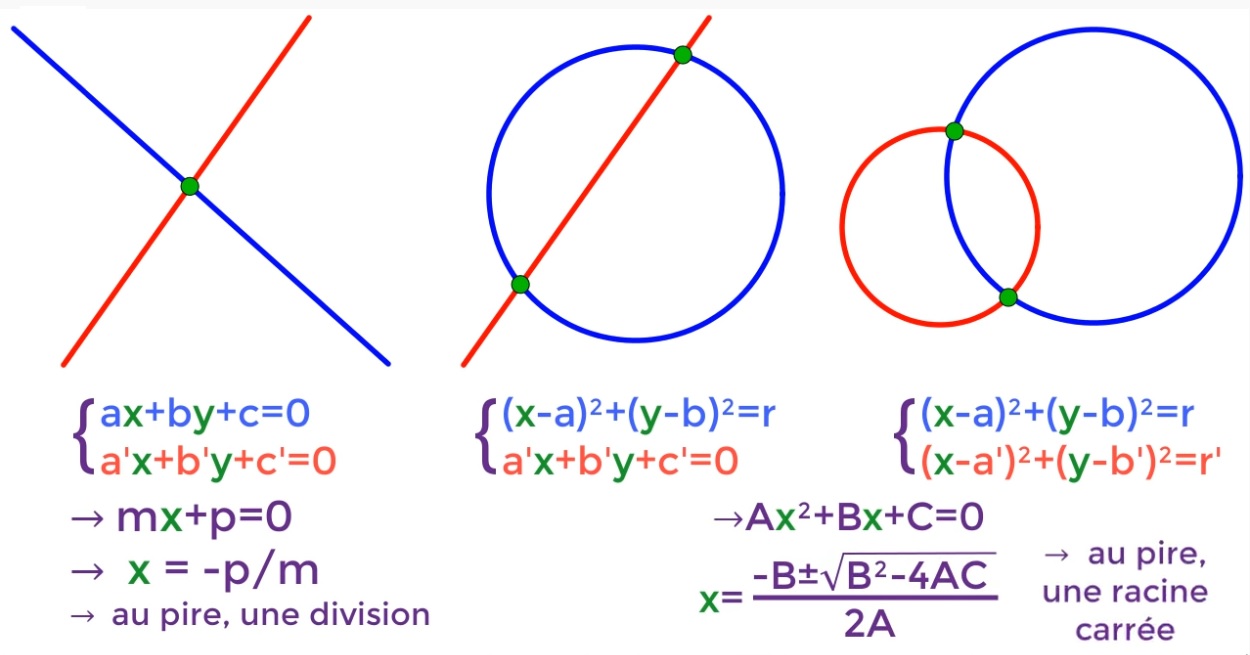
Pour cela, on devra résoudre des systèmes d’équations qui nous donnerons au pire une fraction ou une racine carrée. La racine carrée étant la racine d’une équation du second degrés, une figure est constructible si le polynôme minimal que l’on doit résoudre est de degrés deux. C’est le Théorème de Wantzel.
La vidéo suivante de la page Youtube de El Jj qui explique parfaitement tous cela :
1°/ La quadrature du cercle : Peut-on construire un carré de même aire qu’un cercle donné.
Il y a 4000 ans, en Égypte, il existait une méthode pour assimiler l’aire d’un disque à celle d’un carré.
Cette « recette » magique fut trouver sur le Papyrus Rhind écrit par le scribe Ahmès. Il s’agit d’une « recette » car, si elle permet de trouver une approximation au 100ième de \pi , il n’y a pas de démonstration et on ne parle pas encore du nombre \pi .
Voici ce quelle raconte : l’aire d’un disque de 9 unités de diamètre est égale à l’aire d’un carré de 8 unités de côté.
 |
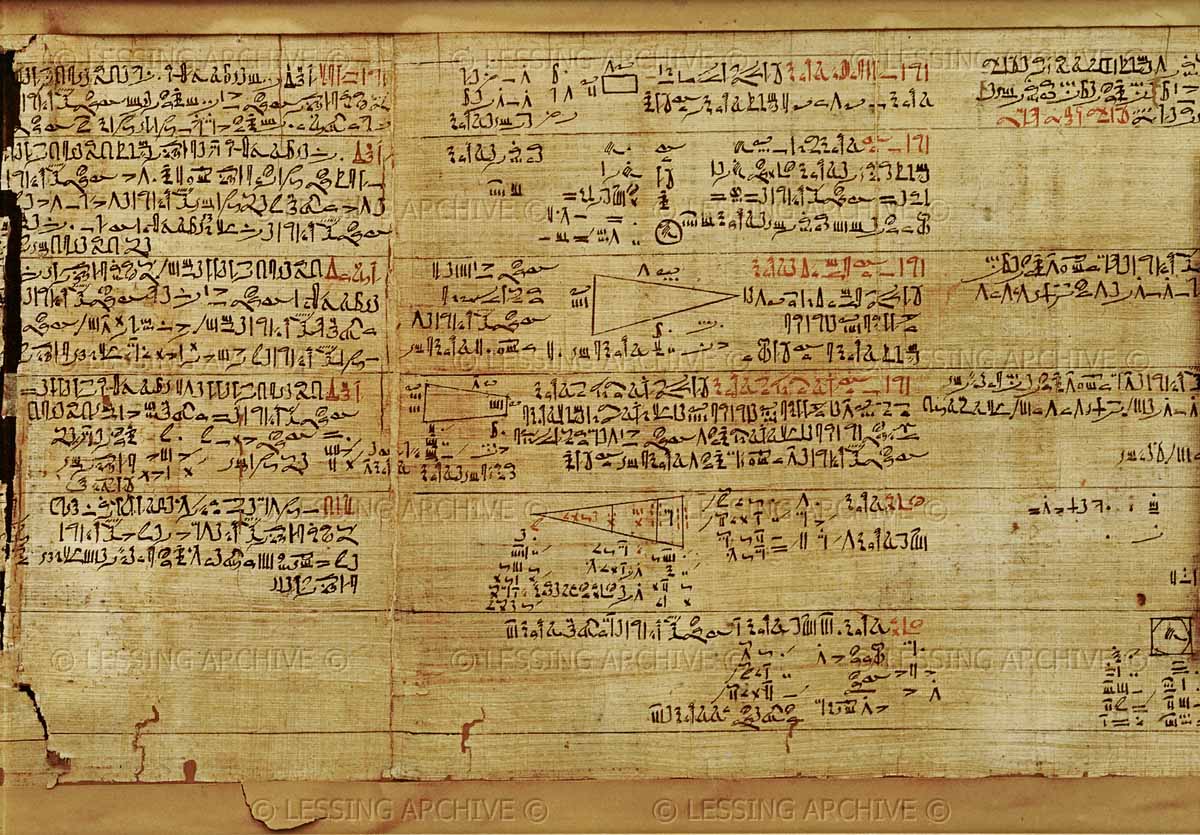Le Papyrus de Rhind est un papyrus de l’ancienne Égypte, datant de la XVème dynastie (vers 1680-1620 avant J.-C.), trouvé à Thèbes en 1858 dans les ruines d’un petit monument proche du Ramesseum par l’égyptologue écossais Alexander Henry Rhinds. |
 |
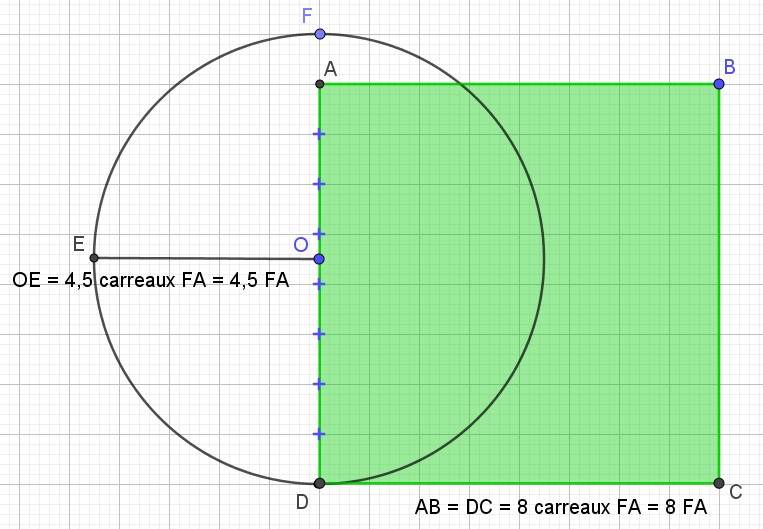Dans un cercle de centre O et de rayon OE = 1 unité, on découpe le diamètre DF en 9 morceaux FA.
Le carré ABCD de côté AB = 8FA aura la même aire que le cercle. Aire Disque = Aire Carré 3,16 au lieu de 3,14 cela fait une erreur de moins de 2 centièmes, ce qui est exceptionnel pour l’époque. |
Il existe une méthode très élégante et exacte mais qui ne respecte pas la géométrie Euclidienne, car elle nécessite de faire rouler un cercle ce qui n’est pas permit par la construction à la règle et au compas.
 |
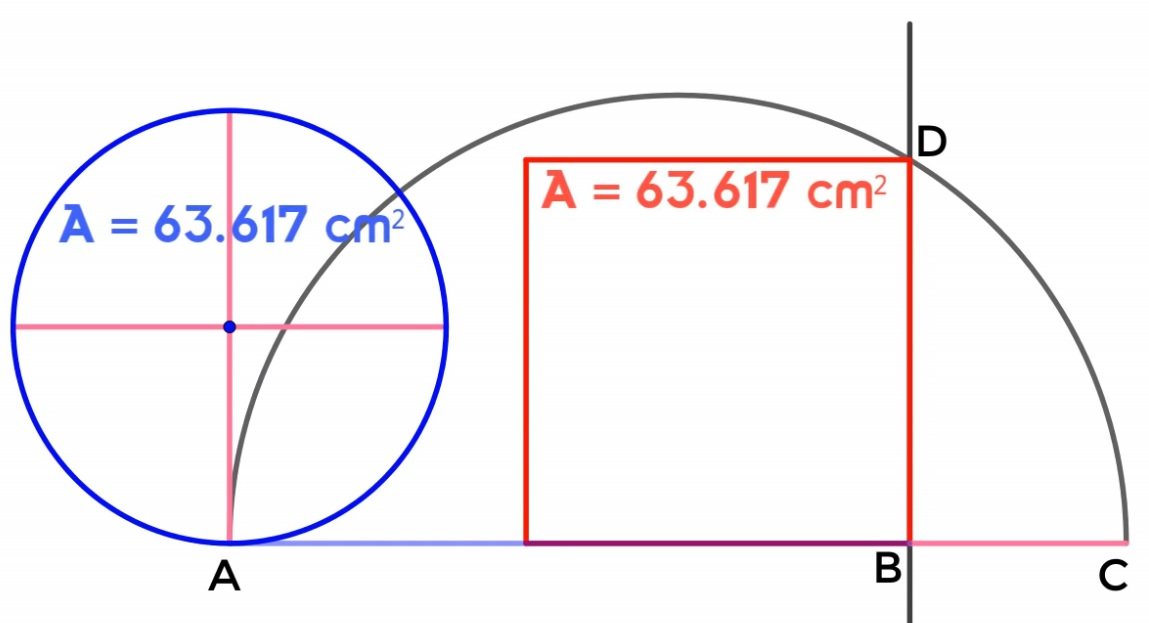– Prenons un cercle de rayon R égal à une unité et faisons-le rouler sur AB = 1/2 Périmètre du cercle. – Rajoutons le rayon du cercle à AB : BC = R – Traçons le cercle de diamètre AC. – Traçons la perpendiculaire à (AC) passant par B, elle coupe le cercle précédent en D. Le carré de côté BD a la même aire que le cercle de départ. |
 |
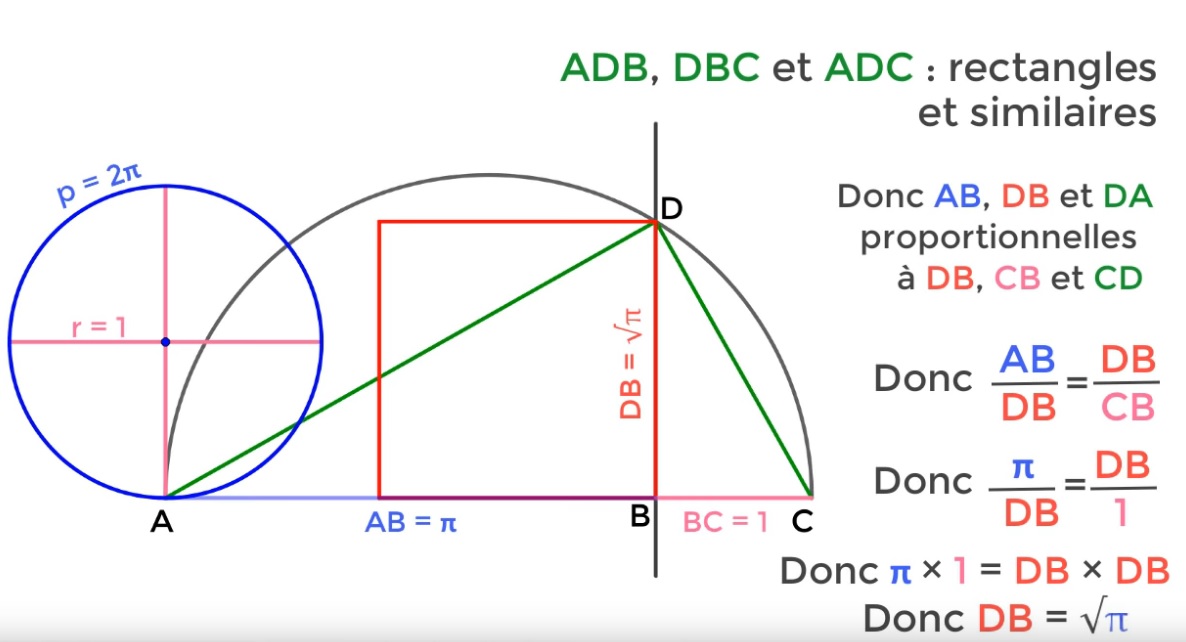Démonstration :
AB = \frac{2\pi R }{2} = \frac{2\pi \times 1 }{2} = \pi Le point D étant sur le cercle de diamètre AC, le triangle ADC est rectangle en D. Aire du cercle = \pi R² = \pi Aire du carré = DB² = \sqrt{\pi }^{2} =\pi |
Pour le fun :
 |
CIRCLE dessiné par Scott KIM (www.scottkim.com) : c’est la quadrature du cercle enfin prouvée.
Dans un carré, on trouve un cercle, enfin les lettres du mot ! |
2°/ La trisection d’un angle :
Est-il possible de couper un angle \alpha en trois angle égaux ?
Pour cela, faisons appel à la trigonométrie, qui nous donne une formule liant un angle à son tiers. On remarque une équation de degrés trois qui nous donnera donc une racine qui sera un nombre non constructible.
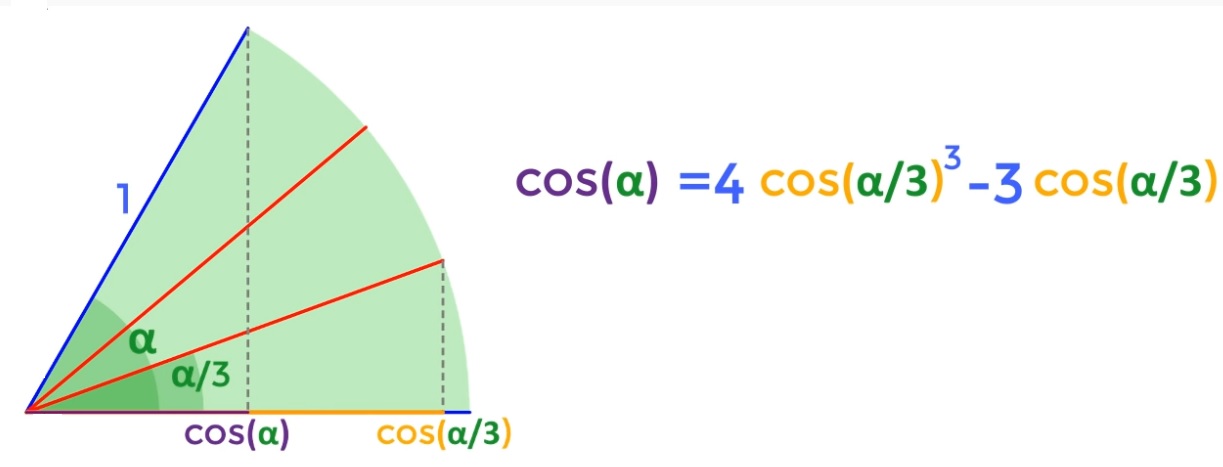
Prenons par exemple un angle \alpha = 60°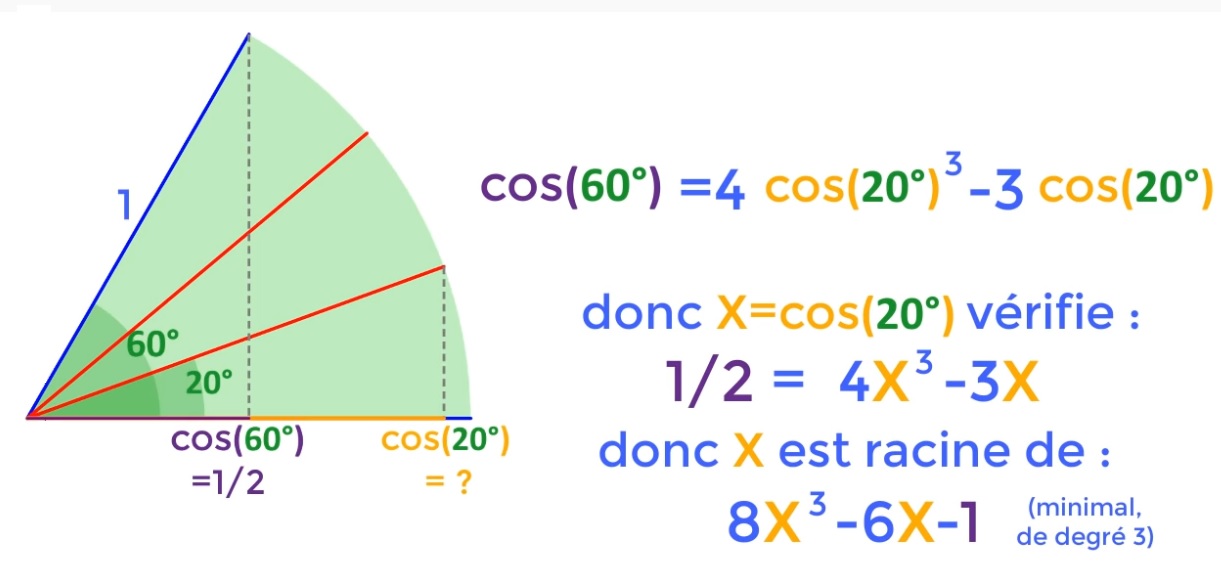
Le polynôme minimal est de degrés 3, donc la trisection d’un angle est impossible.
Cependant Euclide n’a pas précisé si on pouvait plier le support !!
 |
 |
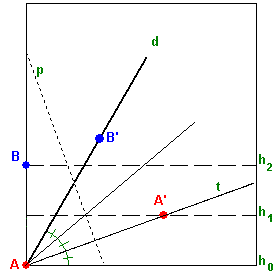| En supposant que l’angle est tracé sur le bord de la feuille (ici, on considère l’angle formé entre le bas de la feuille et la droite d). | – On commence par replier le bas de la feuille pour former les droites h0, h1 et h2. – On plie la feuille la feuille de manière à ce que le point A atteigne h1 et que B atteigne d – Il n’y a plus qu’à tracer AA’, qui trisecte l’angle, l’autre trisectrice n’est pas difficile à obtenir. |
3°/ Duplication du cube :
En 430 av. JC, la légende dit que Les habitants de Délos, en Grèce, furent victimes d’une épidémie de peste et demandèrent à l’oracle de Delphes comment faire cesser cette épidémie. La réponse de l’oracle fut qu’il fallait doubler l’autel consacré à Apollon. Cet autel étant de forme carré, il suffisait de construire un autel carré qui ait le double du volume précédent. Les architectes allèrent trouver Platon pour savoir comment faire. Ce dernier leur répondit que le dieu n’avait certainement pas besoin d’un autel double, mais qu’il leur faisait reproche, par l’intermédiaire de l’oracle, de négliger la géométrie.
En effet, il est impossible de construire un carré qui ait un volume double d’un carré donné, avec seulement une règle et un compas.
Soit C1 un cube de côté c = 1 et donc de volume V1 = c3 = 1
Si on veut construire un cube C2 de volume V2 = 2V1 = 2, alors son côté sera égal à \sqrt[3]{2}.
Le polynôme minimal qui est annulé par \sqrt[3]{2} est x3 – 2, donc \sqrt[3]{2} n’est pas constructible, car ce polynôme minimal est de degrés 3.
IV°/ La géométrie Shadok :
Voici pour s’amuser, un petit cours de géométrie Shadok.
V°/ Des définitions originales :
1°/ La droite : C’est un ensemble infini de points alignés, mais dans les années 1970, un ensemble de Mathématiciens Français a décidé de dépoussiérer les Mathématiques et ils ont tenter d’unifier Algèbre, Géométrie et tout le reste. Ils y sont parvenus, mais le résultat était tellement indigeste qu’il fut rapidement abandonné.
Voici par exemple, la définition de la droite, extraite des commentaires du programme de quatrième de décembre 1971 : version Maths moderne.
Une droite affine D est un ensemble \mathbb{R} muni d’une famille B de bijections de \mathbb{E} sur \mathbb{R} telles que, pour tout f élément de B et pour tout élément (a,b) de \mathbb{R}* ×\mathbb{R}, l’application définie par g(M) = a f(M) + b appartient aussi à B, et réciproquement. L’ensemble E est appelé « le support de la droite affine D », un élément M de E est appelé « un point de la droite affine D ».
2°/ Le centre d’une figure : Qu’est-ce que le centre d’une figure ? Cette question d’apparence anodine est en réalité bien plus riche qu’il n’y paraît. Évidemment, la réponse dépend de la figure.
– Le cercle : le centre d’un cercle est d’autant plus facilement identifiable qu’il intervient dans sa définition même : l’ensemble de tous les points situés à une même distance d’un point donné, et c’est ce point donné qu’on appelle centre. Le centre du cercle précède donc le cercle lui-même.
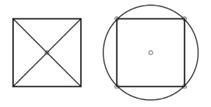
– Le carré : là encore c’est assez simple. Il s’agit par exemple de l’intersection de ses deux diagonales ou encore le centre du cercle qui passe par ses quatre sommets.
– Le triangle : cela devient plus compliqué, car il existe beaucoup de centre pour le triangle. Le centre du cercle inscrit qui est l’intersection des bissectrices, le centre de gravité qui est l’intersection des médianes, le centre du cercle circonscrit qui est l’intersection des médiatrices ou l’orthocentre qui est l’intersection des hauteur.
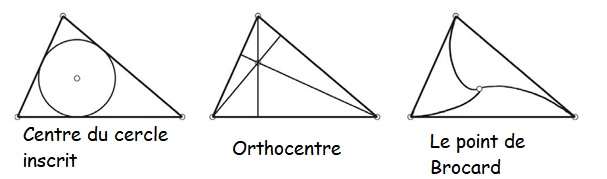
Ça commence à faire beaucoup, et c’est la raison pour laquelle le mathématicien états-unien Clark Kimberling s’est lancé en 1999 dans la rédaction d’une Encyclopédie des centres du triangle (ETC). Le centre du cercle inscrit, le centre de gravité, le centre du cercle circonscrit et l’orthocentre portent respectivement les numéros 1, 2, 3 et 4 dans la numérotation de Kimberling. Au début de l’année 2021, l’ETC répertorie 41 154 centres différents pour un triangle quelconque. Et Clark Kimberling continue régulièrement de la mettre à jour.