Le triangle de Sierpiński, aussi appelé par Mandelbrot le joint de culasse de Sierpiński, est une figure fractale, du nom de Wacław Sierpiński qui l’a décrit en 1915
I°/ La construction :
II°/ Le Théorème de Hutchinson :
III°/ Triangle de Sierpinski par la construction de milieux :
III°/ Particularités :
IV°/ Le triangle de Pascal :
I°/ La construction :
Etape n°1 : on part d’un triangle équilatéral.
Etape n°2 : on découpe ce triangle en 4 triangles équilatéraux, et on enlève celui du milieu.
Etape n°3 : on recommence cette opération dans chaque triangle restant.

II°/ Le Théorème de Hutchinson :
Si, à partir d’une figure finie et bornée, on effectue 3 homothéties de rapport inférieur à 1 et dont les centres sont les sommets d’un triangle équilatéral, et que l’on continue a effectuer ces 3 homothéties à partir des images obtenues, la figure limite obtenue sera TOUJOURS le triangle de Siperski !!!!
III°/ Triangle de Sierpinski par la construction de milieux :
Les 3 points de départs sont les 3 sommets d’un triangle équilatéral. Construire la figure points par points pour observer les milieux, puis par 1000 car le but est qu’il y ait le maximum de points construits.
IV°/ Particularités :
Le paradoxe avec le triangle de Sierpinski, c’est qu’il a un périmètre fini mais une aire nulle, car on enlève des triangles de façon infini.
Le triangle de Sierpiński a une dimension fractale ou une dimension de Hausdorff égale à log 3/log 2, soit environ 1,585. En effet, le triangle de Sierpiński est la réunion de trois copies de lui-même, chacune étant réduite d’un facteur 1/2.
V°/ Le triangle de Pascal :
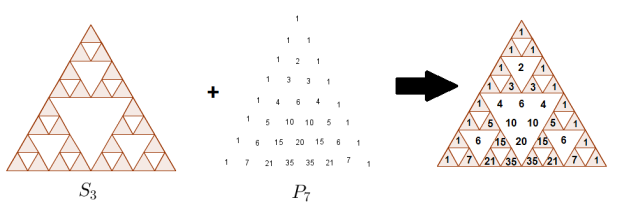
On peut aussi retrouver le triangle de Sierpinski dans le triangle de Pascal. Si on enlève les nombres pairs du triangle Pascal on obtient celui de Sierpinski.

 |
||
| Triangle de Sierpinski | Triangle de Pascal | Les deux |