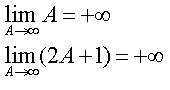A°/ 0,9999…. = 1 ?
B°/ 0,5 kg = 500 kg ?
C°/ 2 = 1 ?
D°/ + 8 = – 1 ?
E°/ 2 m = 2 000 m !
F°/ 4 = 5 !
G°/ Un demi euro est égal à 5 centimes :
H°/ Un euro est égal à 10 centimes :
I°/ 3 = 1 ?
J°/ Tout nombre vaut 1 ?
K°/ p = 2 :
L°/ Sept contre treize :
M°/ 2 = 1 (encore et toujours) :
N°/ 2 = 3 :
O°/ La preuve qu’un trapèze est toujours un parallélogramme :
P°/ La somme de tous les entiers positif est égal à -1/12 ?
Q°/ Le calcul le plus long du monde :
R°/ Des équations pour tout et n’importe quoi :
S°/ 7 = 13 ?
T°/ L’éléphant aussi lourd qu’un moustique :
A°/ 0,9999…. = 1 ?
| Posons : | X = 0,9999…… |
| multiplions X par 10 | 10X = 9,9999….. (1) |
| ajoutons 9 à X | 9 + X = 9,9999….. (2) |
| donc (1) = (2) | 10X = 9 + X |
| déplaçons X | 9X = 9 |
| déplaçons 9 | X = 1 !!!!!!!!!!!! |
Trouver l’erreur dans le raisonnement.
Solution de l’énigme :
- Si on considère que X a un nombre fini de décimales, en faisant 10X on « décale » la virgule d’un chiffre vers la droite. On perd donc une décimale.
Or en faisant 9 + X on « remplace » le 0 par un 9. On a donc le même nombre de décimales.
Conclusion: 10 × X est différent de 9 + X !!!!!!
- Si par contre on considère que X a vraiment un nombre infini de décimale, alors il faut admettre que 0,9999…. = 1. On dira plus exactement que la limite de 0,9999…. sera égale à 1.
En effet : \frac{1}{3} = 0,33333\overline{3}.... \\3 \times \frac{1}{3} = \frac{3}{3} = 1 = 3\times 0,33333\overline{3}.... = 0,99999\overline{9}....
B°/ 0,5 kg = 500 kg ?
A, B, C et D sont 4 nombres quelconques. Alors si A = B et C = D, on a donc A x C = B x D.
Pourtant A = 1 kg = 1000 g = B et C = 0,5 kg = 500 g = D
On en déduit que 1 x 0,5 kg = 1000 x 500 g et que donc 0,5 kg = 500000 g c’est à dire 0,5 kg = 500 kg !
Ou est l’erreur ??
Solution de l’énigme :
En fait, en multipliant des kg par des kg on invente une unité qui n’a aucun sens, les kg² !!!!!
Si quelqu’un est capable de m’expliquer à quoi correspondent des kg² ou des g², je lui offre des cacahuètes !!
Bonne chance
C°/ 2 = 1 ?
Soit X et Y, 2 nombres égaux : X = Y
On multiplie par X : X² = X × Y
On soustrait par Y2 : X² – Y² = (X × Y) – Y²
On factorise : (X + Y) × (X – Y) = Y × (X – Y)
On divise par (X- Y) : X + Y = Y
Or X = Y donc remplaçons Y par X : Y + Y = Y
Donc : 2 Y = Y
On simplifie par Y : 2 = 1 !!!
Où est l’erreur ?
Solution de l’énigme :
Pour passer de : (X + Y) × (X – Y) = Y × (X – Y) à : X + Y = Y
on divise les 2 côtés de l’égalité par (X – Y).
Or (X – Y) = 0.
Et on ne peut pas diviser par 0.
D°/ + 8 = – 1 ?
Soit
A= 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128…
Alors
2A = 2 + 4 + 8 + 16 + 32 + 64 + 128…
et
2A+1 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128…
On a donc : 2A+1 = A
D’où A = -1
Or A est une somme de termes positifs. Comment peut-il être alors négatif ?
De plus A est infini, comment peut-il être égal à -1 ?
Solution de l’énigme :
A ? 2A+1 car A est une somme infinie et que (2A+1) en est une autre mais plus grande.
Si 2A+1 = A alors (2A+1)-A = 0, mais :
E°/ 2 m = 2 000 m !
Prenez d’abord : 1 m = 1000 mm et 2 m = 2000 mm
Multiplions chaque longueur en m entre elles puis de même pour celles en mm. On a donc l’égalité :
1 m × 2 m = 1 000 mm × 2 000 mm
Ce qui fait donc : 2 m = 2 000 000 mm
Soit plus exactement en changeant d’unité : 2 m = 2 000 m
Où est donc l’erreur ?
Solution de l’énigme :
1 m² n’est pas égal 1000 mm². Exercice parfait pour maitriser les calculs avec unités.
F°/ 4 = 5 !
L’égalité suivante est vraie : 16 – 36 = 25 – 45
Soit : 42 – 9 x 4 = 52 – 9 x 5
Soit encore : 42 – 9 x 4 – 81/4 = 52 – 9 x 5 – 81/4
En appliquant une égalité remarquable, on a alors :
(4 – 9/2)2 = (5 – 9/2)2
Soit : 4 – 9/2 = 5 – 9/2
Soit encore : 4 = 5.
Et pourtant 4 n’est pas égal à 5, alors où est l’erreur ?
Solution de l’énigme :
(4 – 9/2)2 = (5 – 9/2)2
(- 4,5)² = (+ 4,5)² Jusque-là tout est vrai.
Mais si a² = b² alors a = ± b et donc a n’est pas obligatoirement égal à b.
G°/ Un demi euro est égal à 5 centimes :
| On sait que 25 centimes est égal à 1/4 d’euro. | 25 cts = 1/4 € |
| Or la racine carrée de 25 est égale à 5 et celle de 1/4 est égale à 1/2. | |
| On en déduit que : 1/2 euro = 5 centimes. | 5 cts = 1/2 € |
Et pourtant 1/2 euro n’est pas égal à 5 centimes, alors où est l’erreur ?
Solution de l’énigme :
Si on peut comparer des centimes avec des euros, on ne peut le faire avec leurs racines carrées qui n’existent pas.
H°/ Un euro est égal à 10 centimes :
| On sait que 100 centimes est égal à 1 euro. | 100 cts = 1 € |
| Or la racine carrée de 100 est égale à 10 et celle de 1 est égale à 1. | |
| On en déduit que : 1 euro = 10 centimes. | 10 cts = 1 € |
Et pourtant 1 euro n’est pas égal à 10 centimes, alors où est l’erreur ?
Solution de l’énigme :
Si on peut comparer des centimes avec des euros, on ne peut le faire avec leurs racines carrées qui n’existent pas.
I°/ 3 = 1 ?
Soient les trois nombres suivants : x = 3 ; y = 1 ; z = 2
donc : x = y + z
Je multiplie par x – y : x(x-y) = (y+z)(x-y)
Je développe : x² – xy = xy + zx – y² – yz
. x² – xy – zx = xy – y² – yz
Je factorise : x(x – y – z) = y(x – y – z)
Soit en simplifiant, x = y
C’est-à-dire : 3 = 1
Solution de l’énigme :
En simplifiant par (x – y – z) = 3 – 2 – 1 = 0, on divise par zéro, ce qui est impossible.
J°/ Tout nombre vaut 1 ?
Soit n un entier quelconque. La formule de la somme algébrique dit :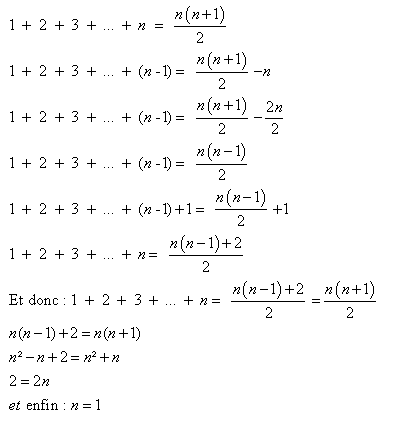
Conclusion : tout entier est égal à 1.
Solution de l’énigme :
L’erreur vient du passage :
1 + 2 + 3 + … + (n – 1) + 1 = 1 + ((n – 1)n)/2
1 + 2 + 3 + … + n = 1 + ((n – 1)n)/2
En effet, les écritures « 1 + 2 + 3 + … + (n – 1) + 1 » et « 1 + 2 + 3 + … + n » ne sont pas égales. Par exemple, si n = 6,
1 + 2 + 3 + … + (n – 1) + 1 = 1 + 2 + 3 + 4 + 5 + 1 = 16
1 + 2 + 3 + … + n = 1 + 2 + 3 + 4 + 5 + 6 = 21
Il faut être très attentif quand on utilise des points de suspension, et il vaut mieux utiliser le symbole Sigma (si on le connaît)
K°/ p = 2 :
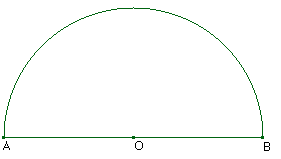 |
Soit AO = BO = 1
Périmètre du ½ cercle = p x R = p = 3.14… |
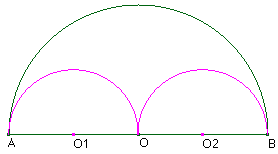 |
Le demi-cercle noir a même périmètre que les 2 demi-cercles roses de rayon 0,5.2 x p x 0.5 |
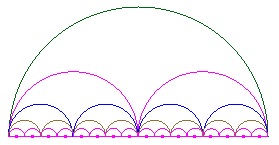 |
Le demi-cercle noir a même périmètre que les 2 demi-cercles roses de rayon 0,5 qui ont même périmètre que les 4 demi-cercles bleus de rayon 0,25 qui ont même périmètre que les 8 demi-cercles bruns de rayon 0,125 qui ont même périmètre que les 16 petits demi-cercles roses de rayon 0,0625. |
Et comme cela indéfiniment, donc le demi-cercle devient son diamètre, et p = 2
Quand on poursuit indéfiniment les constructions proposées, les longueurs des demi-cercles ont effectivement toutes la même longueur et à la fin, ces demi-cercles vont tendre à se confondre avec le diamètre initial.
Pourtant sous les apparences d’une logique inattaquable, il y a une faille dans le raisonnement. Pi est évidemment différent de 2.
La conclusion annoncée ci-dessus est basée sur une fausse interprétation de la « limite » dont la définition précise est la suivante: « Une grandeur variable L a pour limite une grandeur fixe A. Lorsque la différence entre L et A peut devenir et rester moindre que toute quantité donnée à l’avance, aussi petite qu’elle soit. »
Les grandeurs L et A sont ici respectivement le périmètre des demi-cercles et la longueur du diamètre. Mais A est constant et non variable, et la différence entre L et A est également constante.
On ne se trouve donc pas du tout dans les conditions de la définition précédente, et il n’est alors pas surprenant que nous soyons arrivés à un RESULTAT ABSURDE.
L°/ Sept contre treize :
Deux nombres mythiques Sept et Treize se querellaient :
Sept se prenait pour la merveille du monde,
Treize se prétendait le messager du bonheur.
Mais Vendredi les déclara égaux !
Voici comment :
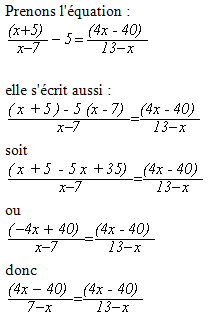
finalement nous avons deux fractions de même numérateur, les dénominateurs sont donc égaux et
7 – x = 13 – x
d’où
7 = 13
– Quoi ? s’écrie Treize consterné, c’est donc que l’équation de départ est fausse et impossible !
– Mais non ! répond Sept tout heureux au Treize devenu porte-malheur,
notre ami x = 1O, solutionne parfaitement cette équation !
En effet, si l’on remplace x par 10 dans l’équation initiale on trouve bien :
L’équation est donc juste.
Donc: 7 = 13
Solution de l’énigme :
Les fractions sont bien égales, leurs numérateurs aussi, mais pas les dénominateurs !
Affirmer cela, revient à simplifier par le numérateur.
Or celui-ci est nul puisque la seule valeur de x satisfaisant l’équation de départ est x = 10. L’équation n’existe que si x = 0.
Or on ne peut pas simplifier par zéro !
Imaginez donc si on pouvait le faire :
on aurait l’égalité de 6 et 458 et bien d’autres choses…
M°/ 2 = 1 (encore et toujours) :
Posons d’abord :
2 = 1 + 1
Multiplions chaque membre par (2 – 1) :
2x(2-1)=(1 + 1)(2 – 1)
Développons:
2×2 – 2×1 = 1×2 – 1×1 + 1×2 – 1×1
Passons 1×2 de droite à gauche :
2×2 – 2×1 – 1×2 = 1×2 – 1×1 – 1×1
Factorisons:
2x(2 – 1 – 1) = 1x(2 – 1 – 1)
En simplifiant les 2 membres par le facteur (2 – 1 – 1), il reste alors :
2 = 1
Il y a une erreur quelque par, mais où ?
Solution de l’énigme :
On ne peut pas diviser par (2 – 1 – 1), car 2 – 1 – 1 = 0 et la division par zéro est impossible.
N°/ 2 = 3 :
On part de l’égalité :
4 – 10 = 9 – 15 = -6
Ajoutons aux deux membres le même nombre : (5/2)² :
4 – 10 + (5/2)²= 9 – 15 + (5/2)²
On fait quelques transformations :
2² – 2x2x5/2 + (5/2)² = 3² -2x3x5/2 + (5/2)²
Par identité remarquable on a :
(2 – 5/2)² = (3 – 5/2)²
En extrayant la racine carrée des deux membres de l’égalité on obtient alors :
2 – 5/2 = 3 – 5/2
Ce qui donne alors : 2 = 3
Il y a une erreur quelque par, mais où ?
Solution de l’énigme :
Lorsque l’on extrait les racines, on oublie les valeurs négatives. En effet :
Si x² = y² alors x = +y ou –y
Dans le cas présent :
Si (2 – 5/2)² = (3 – 5/2)² alors 2 – 5/2 = – (3 – 5/2)
2 – 3 = 5/ 2 + 5/2
1 = 10/2 ce qui est exact !!!
O°/ La preuve qu’un trapèze est toujours un parallélogramme :
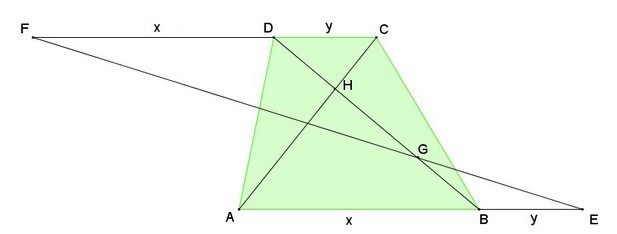
Sur la figure ci-dessus, ABCD est un trapèze quelconque de bases [AB] et [CD].
On pose : AB = x et CD = y.
Les points E et F sont respectivement placés sur les droites (AB) et (CD) tels que : BE = y et DF = x.
Les droites (BD) et (EF) se coupent en G.
Les droites (AC) et (DB) se coupent en H.
En appliquant le théorème de Thalès dans les triangles ABH et CDH, on a :
et donc
En appliquant le théorème de Thalès dans les triangles DFG et BEG, on a :
et donc
Ainsi :
On a ainsi :
Et donc :
C’est à dire que la partie numérique (la valeur absolue) de x est égale à celle de y car HD – GB = – (GB – HD)
Les côtés [AB] et [CD] sont donc parallèles et de même longueur.
On en déduit que le trapèze ABCD est un parallélogramme.
Et pourtant tout trapèze n’est pas un parallélogramme, alors où est l’erreur ?
Solution de l’énigme :
En fait les segments [HD] et [GB] sont égaux, et lorsque l’on divise par (BG – HD), on divise par zéro ce qui est impossible.
De plus, trouver des longueurs négatives est impossible.
P°/ La somme de tous les entiers positif est égal à -1/12 ?
| Posons | A = 1 – 1 + 1 – 1 + 1 – 1 … |
| alors | 1 – A = 1 – 1 + 1 – 1 + 1 – 1 + 1 … |
| donc | 1- A = A |
| cad | A = 1/2 = 0,5 |
| Posons | B = 1 – 2 + 3 – 4 + 5 – 6 … |
| additionnons membre à membre | A + B = 2 – 3 + 4 – 5 + 6 …. |
| donc | -1 + A + B = -1 + 2 – 3 + 4 – 5 + 6 …. |
| ainsi | -1 + A + B = -B |
| on sait que A = 0,5 | B = 0,5 / 2 = 1/4 = 0.25 |
| Somme de tous les entiers | C = 1 + 2 + 3 + 4 + 5 + 6 …. |
| on a | -B = -1 + 2 – 3 + 4 – 5 + 6 … |
| donc | C – B = 4 + 8 + 12 + … = 4 x ( 1 + 2 + 3 +4 +…) = 4 C |
| donc | C = -B/3 = – 0.25/3 = – 1/12 |
Solution de l’énigme :
L’algèbre des séries infinies est un peu particulière. En fait, comme pour l’énigme du A°/ , on compare des infinis qui ne sont pas les mêmes.
A n’est pas égal à 1 – A !!!
Selon comment on écrit A il sera égal à 0 ou 1 :
Dans la série A = 1 – 1 + 1 – 1 + 1 – 1 … , si on prend un nombre pair de termes : A = (1-1) + (1-1) + … = 0
. si on prend un nombre impair de termes : A = (1-1) + (1-1) + … + 1 = 1
Q°/ Le calcul le plus long du monde :
Attribuez un nombre aux 26 lettres de l’alphabet, puis calculer le produit des ces 26 facteurs : (x-a)(x-b)(x-c) … (x-y)(x-z) = ?
Solution de l’énigme :
Ce produit est très long à effectuer, sauf si on se rend compte que l’antépénultième facteur est (x-x) qui est égal à zéro !!
Donc ce calcul est égal à zéro.
R°/ Des équations pour tout et n’importe quoi :
On voit régulièrement des formules faussement scientifiques qui se targuent de mettre le mande en équation, et tant pis si la syntaxe mathématique y est martyrisée (de toutes façons, personne ne va lire la formule…).
La meilleure route du monde :

Variables :
R : Ratio de conduite (le ratio parfait étant de 10)
ab : Décélération lors des freinage (en m·s-2)
al : Accélération latérale durant les virages (en m·s-2)
af : Accélération durant les lignes droites (en m·s-2)
r : rayon des virages (en m)
l : longueur des lignes droites (en m)
v : vitesse(en m·s-1)
- Auteurs : Hermann Tilke, architecte de voiture automobile, Mark Hadley, physicien (Université de Warwick) et John Wardley, concepteur de montagnes russes – étude sponsorisée par Avis, entreprise de location de voitures, et Mercedes-Benz
- Méthodologie : expertise des experts
- Ce que l’on peut conclure de cette formule :
– la meilleure route du monde serait, d’après cette formule, au Portugal. La départementale sarthoise que j’emprunte régulièrement n’est apparemment pas dans le top 25, malgré ses belles lignes droites.
– cette formule peut être en fait simplifiée en R = (temps passé sur les lignes droites) / (temps passé dans les virages). Mais écrite comme ça, la formule aurait été trop simple à appliquer…
– Mark Hadley n’est pas à son coup d’essai en terme d’études un peu absurdes, puisqu’il a aussi étudié les pâtes (pour Giovanni Rana), le Curry (pour Tilda Rice, voir plus bas) ou les Sandwiches (pour Frank PR)
– Les traducteurs français de la page officielle de cette formule n’ont apparemment pas fait S…
Conclusion : cette formule est complètement inutile, et donc, parfaitement dispensable.
Durée d’une relation amoureuse :
Pour les couples hétérosexuels :
L = 8 + 0.5Y – 0.2P + 0.9Hm + 0.3Mf + J – 0.3G – 0.5(Sm – Sf)² + I + 1.5C
Pour les couples homosexuels :
L = 8 + 0.5Y – 0.2P + 2J – 0.3G – 0.5(S1 – S2)² – I + 1.5C
Variables :
L : Temps estimé de la durée de la relation amoureuse (en années)
Y : Temps depuis lequel chacun se connaît (en années)
P : Nombre cumulé d’ex de chacun
Hm : Importance accordée à l’honnêté par l’homme du couple (sur une échelle de 1 à 5)
Mf : Importance accordée à l’argent par la femme (sur une échelle de 1 à 5)
J : Importance accordée à l’humour par chacun, cumulé (sur une échelle de 1 à 5)
G : Importance accordée à la beauté par chacun, cumulé (sur une échelle de 1 à 5)
Sm et Sf / S1 et S2 : Importance accordée au sexe par chacun (sur une échelle de 1 à 5)
I : Importance accordée à la belle famille (sur une échelle de 1 à 5)
C : Importance accordée aux enfants (sur une échelle de 1 à 5)
- Auteur : Inconnu, étude commandée par MSN – 2014
- Méthodologie : sondage sur 2000 personnes
- Ce que l’on peut conclure de cette formule :
– Pour faire durer une relation de couple, il faut se connaître depuis longtemps mais ne pas avoir eu d’autres partenaires auparavant.
– Au maximum, une relation née d’un coup de foudre peut durer 31.2 ans.
– Une relation hétérosexuelle durera plus longtemps si chacun s’entend bien avec se belle famille, le contraire pour une relation homosexuelle.
– Un couple homosexuel qui accorde de l’importance à l’humour durera plus longtemps qu’un couple hétérosexuel qui y accorde la même importance.
– En ajoutant des grandeurs sans unités, on peut obtenir des durées
Conclusion : cette formule est complètement con.
Meilleures conditions pour boire une bière :
E = – (0,62 T² + 39,2W² + 62,4P²) + (21,8T + 184,4W + 395,4 P + 94,5 M – 90,25V) + 50 (S + F + 6,4)
Variables :
E : Plaisir ressenti lors de la dégustation d’une bière
T : Température, en °C
W : Temps avant de retourner travailler, en jours
P : Nombre de personne avec qui l’on partage cette bière
M : Humeur (sur une échelle de 1 à 5, 1 = sale journée)
V : Volume du fond sonore (sur une échelle de 1 à 5, 1 = très fort)
S : Qualité de la nourriture disponibles (sur une échelle de 1 à 5)
F : Qualité des snacks disponibles (sur une échelle de 1 à 5)
- Auteurs : mathématiciens du MindLab (Université du Sussex), étude commandée par Taylor-Walker, une chaîne de pubs britannique.
- Méthodologie : sondage sur 1000 personnes, questionnaire disponible en ligne
- Ce que l’on peut conclure de cette formule :
– La meilleure bière se déguste à 17.6 °C
– La meilleure bière se déguste le vendredi soir
– La meilleure bière se partage avec 3 personnes
La formule ne tient cependant pas compte de nombreux autres paramètres inclus dans l’étude : catégorie socio-économique, âge, sexe, région…
Conclusion : Cette formule inutilement compliquée ne mérite pas vraiment ses coefficients à 4 chiffres significatifs
Équation du curry parfait :
Ppar Mark Hadley, physicien à l’Université de Warwick (le même qui a pondu la formule de la meilleure route) (2013)
Étude commandée par la marque de riz Tilda

En fait, cette formule est une simple application de formules de volumes, mais elle s’accompagne d’une suggestion de présentation basée sur le nombre d’or. L’équation est donc incontournable !
Équation du sapin parfait :
Par Nicole Wrightham et Alex Craig, étudiants de l’Université de Sheffield (2012)
Étude commandée par la chaîne de magasins Debenhams

L’équation aurait demandé deux heures complètes de travail acharné…
Équation du parfait derrière :
Par David Holmes, psychologue à l’Université métropolitaine de Manchester (2006)
Étude sponsorisée par la marque de boisson Lambrini

Équation à prendre avec de très grosses pincettes, la plus fiable de mes sources est FoxNews. D’autant que, selon cette formule, si le rapport tour de hanche / tour de taille est égal à la texture de la peau, alors on serait en présence d’un fessier infiniment parfait…
Effet de la bière sur la vision (« beer google ») :
Par Nathan Efron, optométriste à l’Université de Manchester (2005)
Étude commandée par Bausch & Lomb, une marque de produits médicaux optique et par Speed dater, une entreprise de speed-dating

Équation de la plage parfaite :
Par Dimitrios Buhalis, professeur en Management et Marketing à Université de Surrey (2005)
Étude commandée par l’agence de voyage Opodo par faire un top 25 des meilleures plages
Encore une fois, débrouillez-vous pour mesurer objectivement toutes ces variables
Équation du film d’horreur parfait :
Par des scientifiques du King’s College de Londres (2004)
Étude commandée par la chaîne de télé Sky Movies
Faute de source fiables, je n’ai aucune idée de ce que la formule calcule, encore moins des unités, ni de ce que signifie vraiment ce sin x – 1. Cette formule n’est maintenant rien d’autre que des lettres posées aléatoirement les unes à côté des autres…

Équation du jour déprimant :
Signé par le psychologue (?) Cliff Arnall (mais qui aurait été écrite par une agence de pub) (2006)
Etude commandée par la chaîne de télé Sky Travel (chaine qui a fermé, contrairement à sa grande soeur Sky movies)
Cette formule, qui n’a pas le moindre sens mathématique, a donné naissance au blue monday, un marronier journaliste qui prétend que le troisième lundi de janvier serait le jour le plus déprimant de l’année. Même son auteur a reconnu quelmques années plus tard que c’était n’importe quoi.
S°/ 7 = 13 ?
| Voici une équation : | \frac{x+5}{x-7} - 5 = \frac{4x-40}{13-x} |
| Réduisons au même dénominateur | \frac{x+5 - 5(x-7)}{x-7} = \frac{4x-40}{13-x} |
| Effectuons |
\frac{4x - 40}{7-x} = \frac{4x-40}{13-x}
|
| Les numérateurs étant égaux, les dénominateurs le sont aussi |
7-x = 13 - x
|
| Et donc : | 7 = 13 |
7 est donc égal à 13 !!! Il y a un problème ou alors il va falloir reprendre les règles d’algèbre depuis le début.
Solution :
| Cherchons la solution de l’équation de départ | \frac{x+5}{x-7} - 5 = \frac{4x-40}{13-x} |
| Équation qui peut donc aussi s’écrire | \frac{4x - 40}{7-x} = \frac{4x-40}{13-x} |
| Effectuons le produit en croix | (4x - 40)(13-x) = (4x-40)(7-x) |
| Factorisons | (4x - 40)(13-x-7+x) = 0 |
| Effectuons | 6(4x - 40) = 0 |
| La solution de l’équation est donc : x = 10 | 4x - 40 = 0 \ donc : x = 10 |
Or on a affirmé que si les numérateurs sont égaux, les dénominateurs le sont aussi. Cela est parfaitement exact sauf si les numérateurs sont nuls car alors les fractions seraient égales à zéro et les dénominateurs pourraient être égaux à n’importe quel nombre. En effet : \frac{0}{7} = \frac{0}{13} = 0
La solution de l’équation étant x = 10 alors 4x - 40 = 0 et on ne peut donc pas affirmer que les dénominateurs x-7 et 13-x sont égaux.
T°/ L’éléphant aussi lourd qu’un moustique :
|
Posons : e = poids de l’éléphant , m = poids du moustique et 2p = poids des 2 animaux en imaginant que c’est un nombre pair.. e + m = 2p Donc : e = m L’éléphant pèse autan que le moustique !!!!!!!
|
 |
Solution :
Toutes les étapes sont correctes sauf à l’équa. 3. Il s’agit d’une équation du second degrés, donc il y a 2 solutions :
Par exemple si e = 5 kg (c’est vrai il est pas très gros) et m = 1 kg (bon lui il a bien profité) alors p = 3 kg
e + m = 5 + 1 = 6 = 2×3 = 2p
équa. 3 : (e – p)² = (5 – 3)² = 2² = 4 et (m – p)² = (1 – 3)² = (-2)² = 4
L’équation 3 est correcte car 4 = 4 mais 2 n’est pas égal à -2, ce sont leurs carrés qui sont égaux.
Si x² = y² alors x = y ou x = -y
| Soit : e – p = m – p Alors e = m mais ce sera faux. |
Soit : e – p = -m + p |