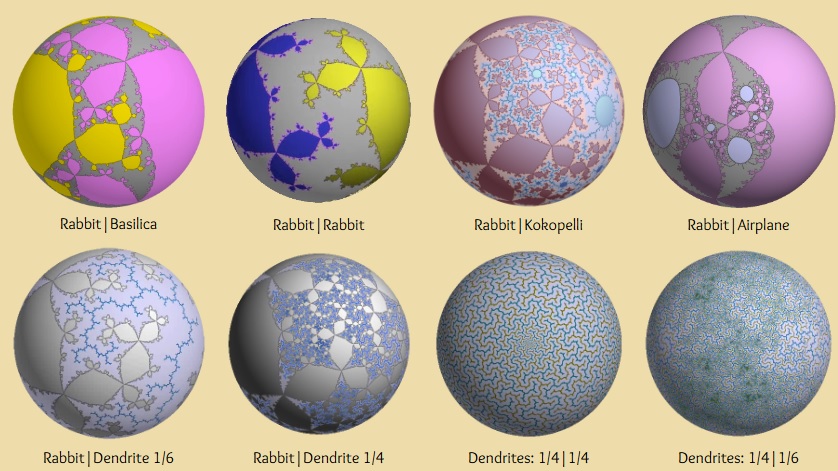
Une figure fractale est un objet mathématique qui présente une structure similaire quelque soit l’échelle à la quelle on la regarde.
I°/ Des vidéos :
II°/ C’est quoi une fractale ?
III°/ Dans la nature :
IV°/ Construction et dimensions particulières :
V°/ Le Paradoxe du littoral :
VI°/ Animations Géogébra :
I°/ Des vidéos :
Un artiste très imaginatif : Jos Leys |
Un artiste très imaginatif : Jos Leys |
Un site avec de très belles animations sur des sphères :
II°/ C’est quoi une fractale ?
Quelle est donc la particularité d’une figure fractale ?
| Si on zoome sur une figure classique (polygone ou cercle), on trouvera un segment comme élément de base. Le cas le plus particulier est celui du cercle. En effet si on choisi de zoomer sur un point de ce cercle, celui-ci va s’aplanir jusqu’à présenter un segment. Ce détail ne nous permet pas de reconstituer l’objet de départ. | Si on zoome sur une partie d’une figure fractale, et bien on retrouvera toujours un détail et ce, quelque soit la puissance du zoom. La figure fractale est donc de taille infinie. De plus, si la fractale est auto-similaire, ce détail sera identique à la figure fractale de départ. |
Cela donne des figures de toutes beautés : cliquez sur une image pour lancer le diaporama.
III°/ Dans la nature :
On en trouve aussi dans la nature :
 Le choux Romanesco avec ces mini choux à l’infini.. |
 Les fougères, qui sont des reproductions d’elles même, quelque soit le niveau où on les regarde. |
 Les branches des arbres sont elles aussi des ramifications. |
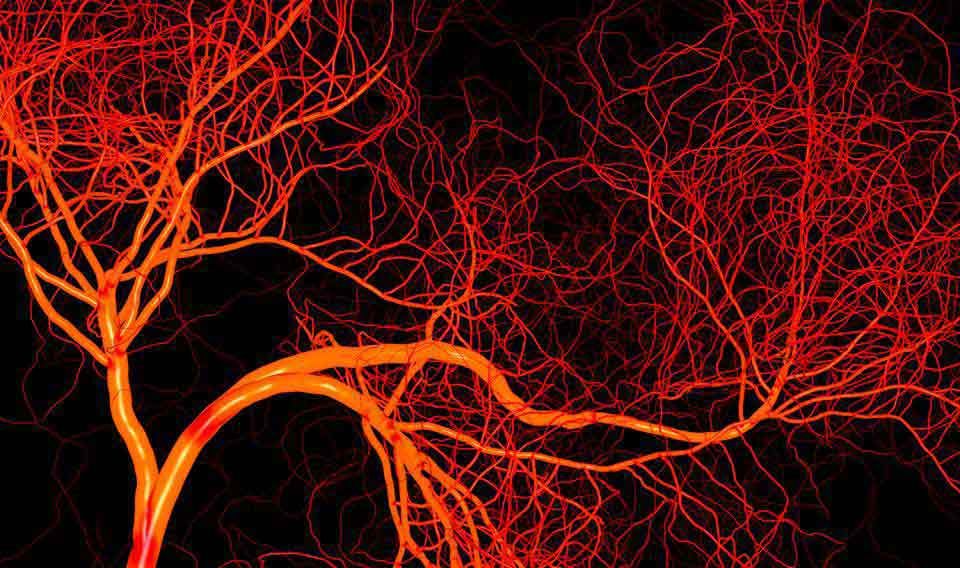 Les vaisseaux sanguins du corps humain sont des ramifications qui se répètent sans cesse. |
 Le magnifique tournesol |
 l’Aloès spirale (Aloe Polyphylla) |
 Kaori (Agathis Australis) |
 Crassula Capitella |
IV°/ Construction et dimensions particulières :
Mais cela ouvre aussi la porte à des abstractions mathématiques qui heurte notre logique. Une ligne est de dimension 1, une surface de dimension 2 et un volume de dimension 3. Mais de quelle dimension est une ligne fractale. Selon toute logique, si c’est une ligne alors sa dimension est de 1. Vérifions cette affirmation avec la célèbre courbe de Von Koch, découverte en 1904 par le mathématicien Suédois Elge Von Koch.
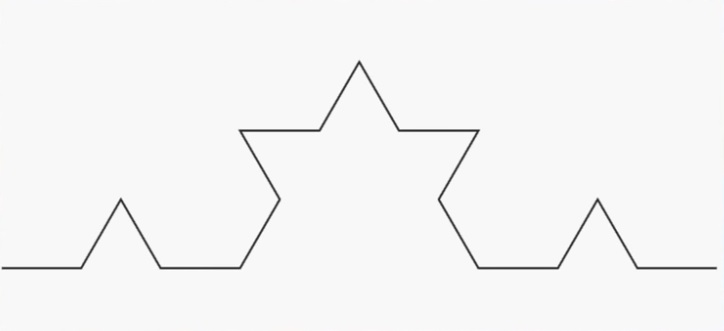
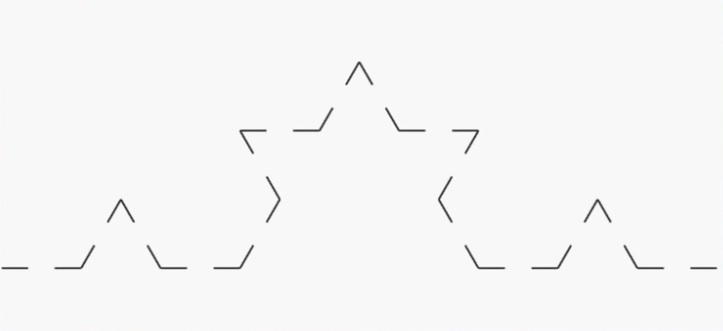
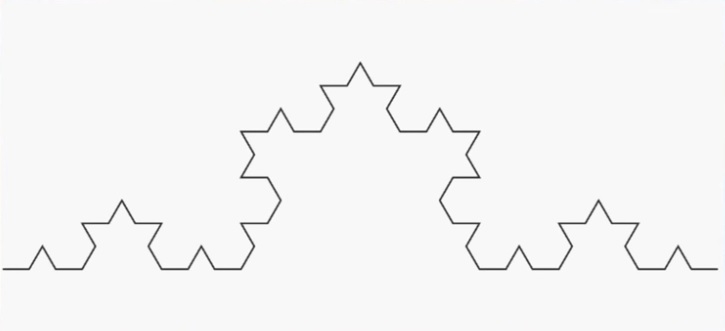
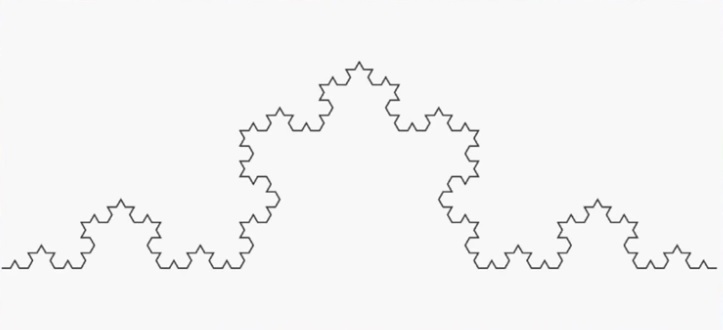
La construction de la courbe de Von Koch est simple :
 |
 |
 |
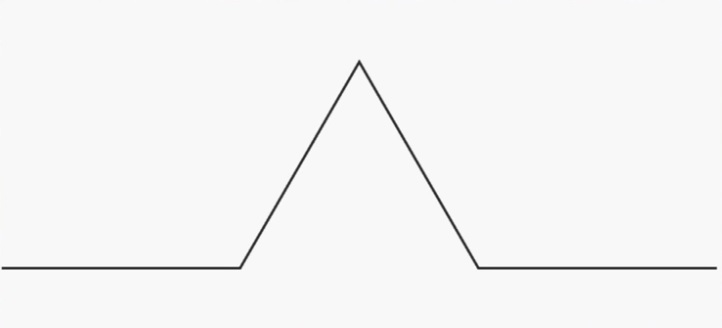| Prenons un segment de longueur L. Longueur = L |
Découpons-le en trois et enlevons le tiers du milieu. Longueur = 2L/3 |
Dans cet espace libre, plaçons deux segments de longueur L/3. Longueur = 2L/3 + 2L/3 = 4L/3 = L + L/3 |
 |
 |
 |
 |
 |
 |
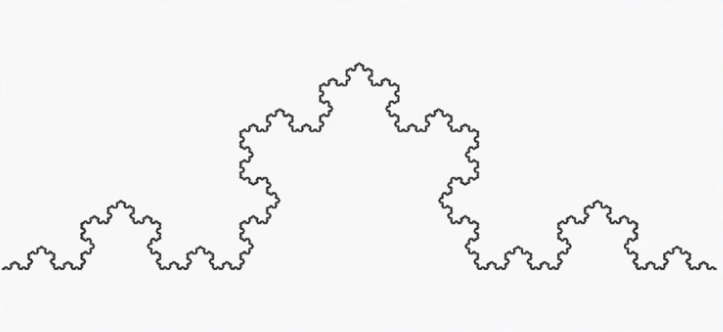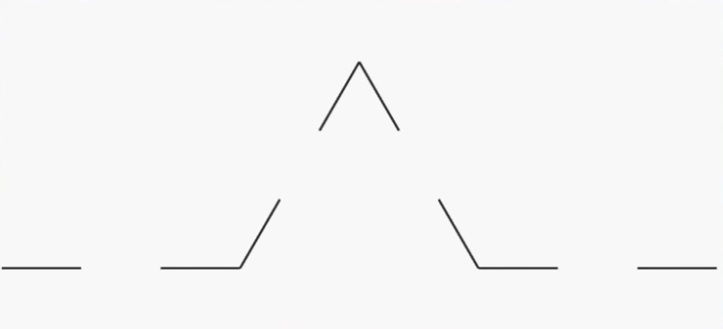
A chaque étape de la construction, la longueur de la ligne augmente de un tiers. Comme le nombre d’étape est infinie, la courbe de Von Koch est donc infinie, alors quelle tient parfaitement sur une feuille et que l’on voit bien où elle démarre et où elle finie.
Mais quelle est sa dimension ? Pour rappel, quand on multiplie les longueurs par k alors les surfaces sont multipliées par k² et les volumes par k3.
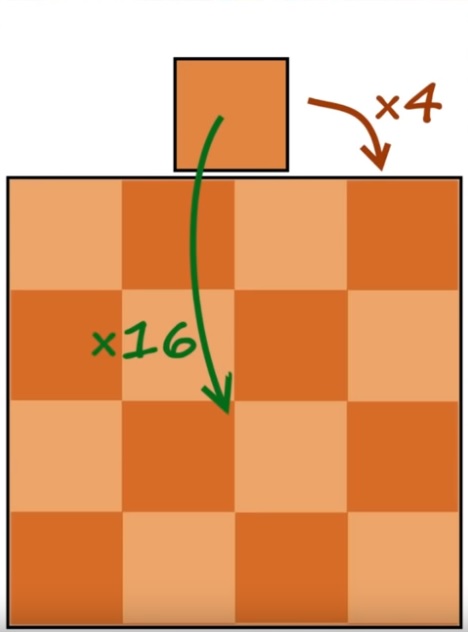
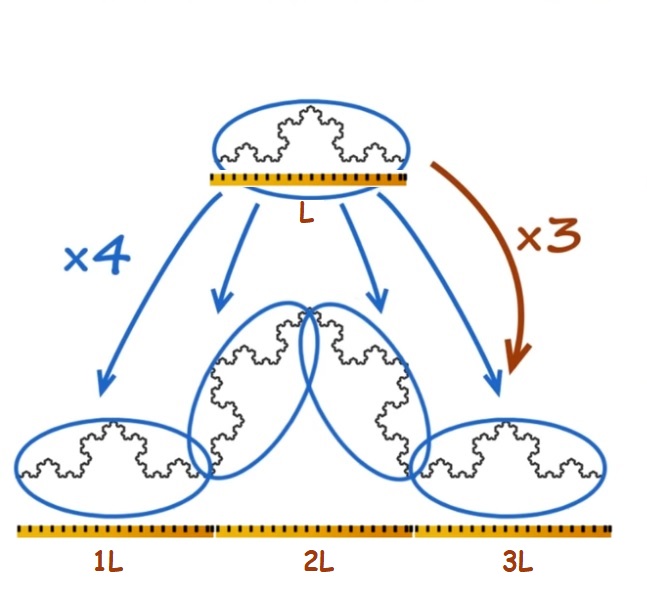
Et bien si on multiplie une courbe de Von Koch par 3 et bien on se rend compte que l’on a 4 exemplaires de la ligne de départ.
| Périmètre | Surface | Volume | Courbe de Von Koch | |
| Multiplier par | \times k | \times k² | \times k3 | \times kn |
| Multiplier par | \times 3 | \times 3² = 9 | \times 33 = 27 | \times 4 |
| Dimension | 1 | 2 | 3 | \approx 1,2618… |
Donc : 3n = 4
Passons par les logarithmes pour déterminer la valeur de n : Log 3n = Log4 et donc nLog 3 = Log 4 et enfin : n = \frac{Log 4}{Log 3}\approx 1,2618…
La dimension de la courbe de Von Koch est une valeur intermédiaire entre 1 et 2. Ces dimensions intermédiaire s’appellent des dimensions d’Hausdorff du nom du mathématicien Allemand Felix Hausdorff. On mesurera donc la courbe de Von Koch en mètre1,16. Liste de fractales par dimension de Hausdorff.
V°/ Le Paradoxe du littoral :
Une application aussi géniale que perturbante est le Paradoxe du littoral. Dans les années 1920, le mathématicien Anglais Levis Fry Richardson décide de mesurer la longueur des côtes Anglaises.
Il se rend compte que suivant l’unité de mesure que l’on choisit, cette longueur peut varier de façon considérable. En effet, si on les mesure avec des lignes de 100 km a long, les côtes Anglaises mesurent 2 800 km, mais elles passent à 3 400 km si on les mesure avec des lignes de 50 km. Avec des lignes de 100 km on néglige beaucoup de détail.
 |
 |
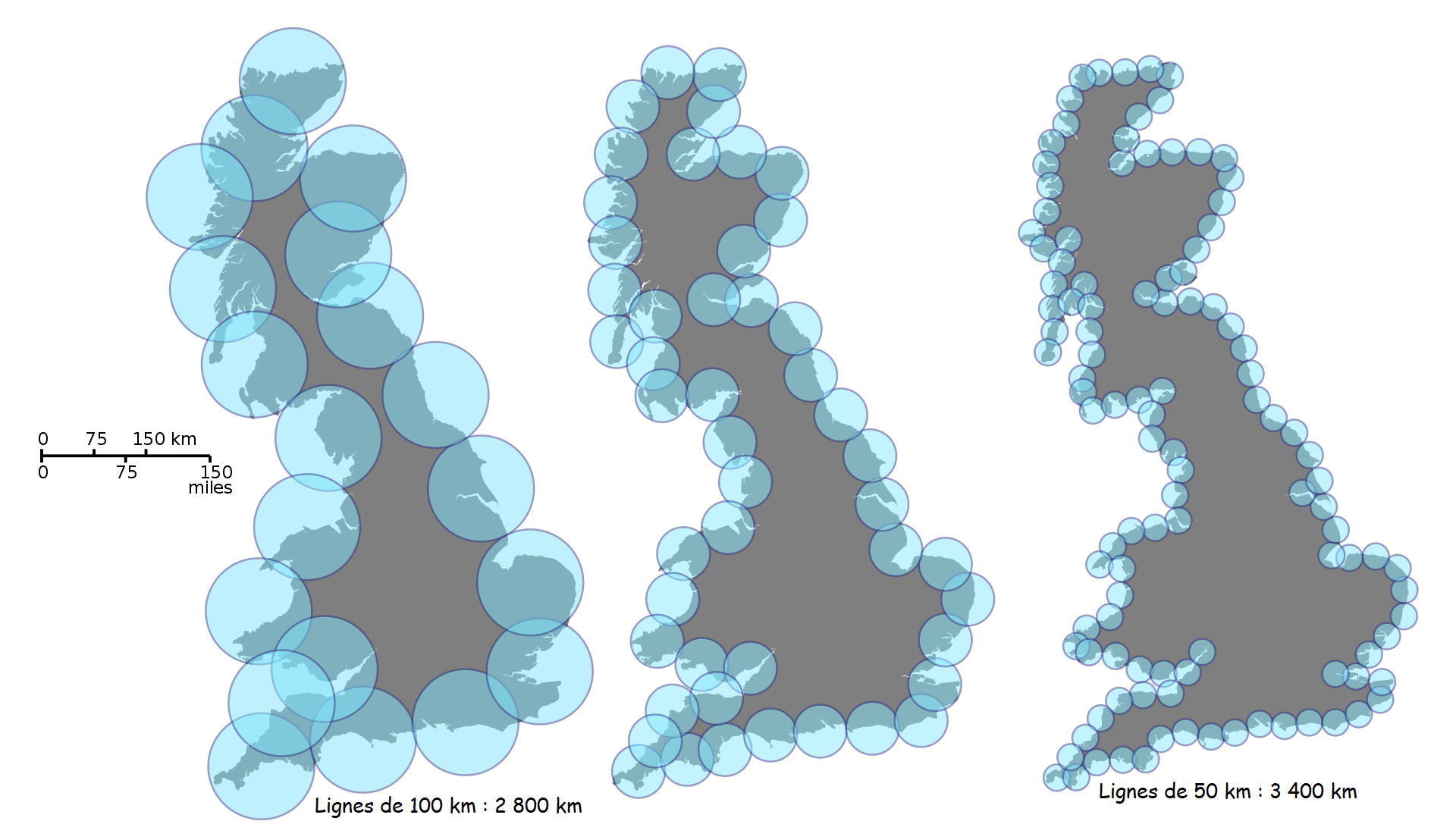
| On peut même imaginer que les traits de côtes sont infinis si on va jusqu’à l’atome de chaque grain de sable !!! | Pour des côtes très découpées, plus on s’approche du détail et plus la longueur augmente. Par exemple Les États fédérés de Micronésie, qui sont de petites îles perdues dans l’océan Pacifique, ont une surface de 702 km2 pour un périmètre de 6 112 km. C’est-à-dire que la longueur de côte est presque neuf fois plus grande que la surface, en valeur numérique. |
Plus fort encore, le Canada a un périmètre de 210 973 km c’est à dire plus de cinq fois la circonférence terre.
Il existe principalement deux ressources listant les longueurs des littoraux de la planète. La première est le World Factbook, un document conçu et publié par la CIA, l’agence de renseignements américaine ; la seconde vient de la World Ressources Institute (WRI), une organisation environnementale américaine. Ces deux structures disposent de moyens techniques d’une grande précision et le sérieux de leurs travaux est incontestable. Et pourtant, sur près de deux cents pays répertoriés, les deux organisations semblent dans l’incapacité la plus totale de trouver le même résultat en effectuant la même mesure. La différence à propos de Madagascar est particulière.
| World Factbook (WF) | World Ressources Institute(WRI) | Erreur WRI par rapport à WF | |
| Canada | 202 080 km | 265 523 km | 31 % |
| Japon | 29 751 km | 29 020 km | -2,5 % |
| Grèce | 13 676 km | 15 147 km | 10,8 % |
| Madagascar | 4 828 km | 9 935 km | 105,7 % |
| Nouvelle-Zélande | 15 134 km | 17 209 km | 13,7 % |
VI°/ Animations Géogébra :
Quelques exemples de figures fractales : une page avec des fractales en Géogébra.
| Le triangle de Sierpinski | Le carré de Sierpinski |
| Le flocon de Koch | Arbre de Pythagore |
| Arbre de Pythagore | L’éponge de Menger (cliquer sur l’image.) |
 |