La puissance des Mathématiques est prodigieuse. La preuve réside dans son utilisation durant l’Antiquité, car nos ancêtres ont réalisé des travaux exceptionnels à l’aide de moyens dérisoires et de raisonnements Mathématiques vraiment très simples.
Bien avant Jésus Christ, les Mathématiciens de l’Antiquité étaient capables de bien des performances :
≈ 580 Avt JC : Thalès généralise le théorème qui porte maintenant son nom. On peut mesurer des distances inaccessibles comme la hauteur d’une pyramide, d’une muraille protégée par des ennemis ou la largeur d’une rivière en crue.
≈ 550 Avt JC : Pythagore généralise le théorème qui porte maintenant son nom. Les angles droits sont désormais réalisables et les bâtiments prennent de la hauteur.
≈ 350 Avt JC : Aristote affirme que la Terre est ronde. Il faudra attendre le XVIIIème siècle et Galilée pour en être sûr et ne pas risquer le bucher de l’inquisition.
≈ 270 Avt JC : Aristarque mesure la taille de la Lune, du Soleil, les distances Terre-Lune et Terre–Soleil et cela en restant sur notre bonne terre et sans instruments modernes.
≈ 220 Avt JC : Ératosthène mesure la circonférence de la Terre et valide la rotondité de la terre.
≈ 150 Avt JC : Hipparque pose les premières bases de la trigonométrie et calcule avec précision la distance Terre – Lune. Les angles ne sont plus un problème.
Avec l’Almageste de Ptolémée, la théorie Géocentrique s’impose comme une évidence et est reprise ensuite par les religions. Nous avons donc une modélisation de référence, fausse, mais totalement ancrée. Le modèle étant faux, plus aucune avancée ne pouvait être faite car nous étions dans une impasse. S’en suivi près de 1500 ans où aucune découverte ne fut faite (ou du moins publiée)… Quel gâchis !
Ici un historique complet.
Ici un blog très détaillé mais un peu austère.
I°/ La terre est-elle ronde ? Pas de platiste dans l’Antiquité
II°/ Astronomie : c’est la terre ou le soleil qui est au centre de l’univers ?
III°/ Circonférence de la terre et distance terre – lune – soleil : Érathostène (-310 -230 avt. JC) et Aristarque de samos (-310 -230 avt. JC)
IV°/ Le tunnel de Samos : Creuser un tunnel de 1 km sous la montagne 550 ans avant J.C.
V°/ Poids des planètes : Kepler (VI°/ Vitesse de la lumière :
VII°/ Les instruments de mesure de l’antiquité :
VIII°/ L’équation d’Al-Khwarizmi : 780-850 après JC
I°/ La terre est-elle ronde ?
De nos jour il existe encore des platistes qui croient que notre bonne vielle terre est plate. Cependant, avec les satellites, le doute n’est plus permis. Mais dans l’antiquité, comment connaître la forme exacte de notre planète ? Et bien avec de l’observation et un minimum de réflexion, ce qui manque toujours aux platistes à l’encéphalogramme … plat. Une série de vidéos Youtube qui analyse les théories platistes.
1°/ Un bateau apparaît petit à petit à l’horizon :
 |
Lorsqu’un navire navigue vers l’horizon, il ne devient pas de plus en plus petit jusqu’à devenir invisible comme il le ferait si la Terre était plate. Sa coque semble d’abord disparaître puis son mât. Ceci est due à la courbure de la terre qui laisse apparaitre le mât plus longtemps que la coque. Il faut bien entendu se munir de jumelle pour observer ce phénomène car l’œil humain ne peut pas voir trop loin. Sur le bord d’un lac on dispose un laser qui pointe sur la cible d’un bateau qui navigue sur le grand lac. Si la terre est plate, alors le rayon laser restera parallèle à la surface du lac, sinon on observera un écart. Or c’est bien ce que l’on voie : à 5 km du laser l’écart est de 1,80 m et il est de 7,3 m à 10 km. |
2°/ Notre ombre sur la Lune :
 |
 |

Lors d’une éclipse lunaire, la Terre se trouve exactement entre le Soleil et notre satellite naturel. On peut alors apercevoir l’ombre de la planète bleue, qui est toujours un cercle, ou une partie de cercle selon le moment de l’éclipse. Or, on ne voit jamais une ligne qui serait l’ombre d’une planète plate vue par la tranche. Si la Terre était plate, pour expliquer l’ombre circulaire, il faudrait que le Soleil soit toujours à « minuit » lors d’une éclipse lunaire pour créer un cercle parfait, ce qui n’est pas le cas, car l’heure d’une éclipse varie selon notre localisation sur la planète. |
3°/ La voûte céleste diffère selon l’endroit :
 |
C’est à Aristote (384 à 322 avant notre ère) que l’on doit la première observation de la différence de position des constellations selon l’endroit où l’on se trouve (faite lors d’un périple en Égypte). Son observation est vraiment très simple : si deux personnes observe la voûte céleste dans deux endroits différents et bien ils n’observeront pas la même chose car ils ne regardent pas dans la même direction. |
4°/ L’existence des saisons :
 |
Le changement de saison – l’hiver en Australie et l’été au Canada en même temps, par exemple – s’explique par l’angle des rayons solaires sur la Terre. Si cette dernière était plate, nous aurions exactement les mêmes saisons en même temps, car l’angle serait toujours le même, peu importe où l’on se trouve. Ce qui n’est manifestement pas le cas. Dans l’antiquité on pouvait déjà voyager sur de longue distance pour observer ce changement de saison. |
5°/ Les levers et couchers de soleil :
 |
En observant un levé de soleil depuis le sommet d’une montagne, on peut aisément voir la course du soleil qui suit une trajectoire circulaire. Si la terre était plate, le jour apparaitrait de la même façon partout sur terre. |
6°/ On voit plus loin de plus haut :
 |
Plus vous êtes haut, plus vous voyez loin. Faites le test. Au sol, sans rien qui vous bloque la vue, regardez au loin à travers des longues-vues. Ensuite, grimpez dans un arbre, ou montez au sommet d’un édifice, et refaites l’expérience. Plus vous serez haut, plus vous verrez loin. Ce phénomène facilement observable est dû à la courbure terrestre. À titre d’exemple, si vous faites 1,80 m de haut, votre horizon sera situé à cinq kilomètres de vous. Si vous gravissez l’Everest, il sera à… 370 kilomètres. |
Un platiste marseillais pourrait vous faire remarquer que l’on peut voir le sommet du Canigou depuis Marseille, alors que la courbure de la terre devrait l’interdire. Ce phénomène optique existe bel et bien, et il est du à la réfraction atmosphérique. Il nécessite des conditions de pression, de température et d’humidité de l’atmosphère, bien particulières.
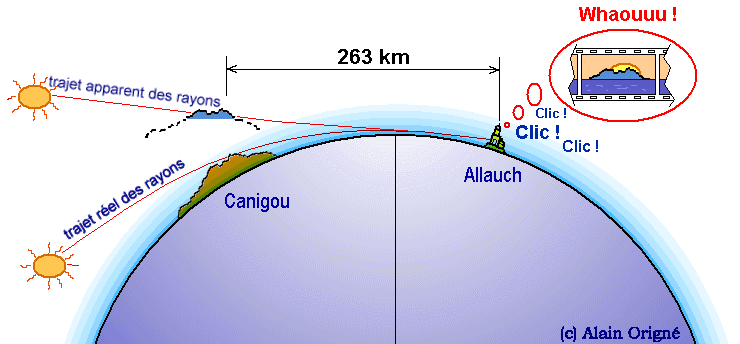
Cliquer sur l’image pour plus d’explications. |
7°/ La ligne s’enfonce sous l’horizon :
 |
Un exemple analogue à l’expérience avec les bateaux est à chercher du côté des infrastructures humaines longues installées sur de grandes surfaces d’eau. Un exemple très parlant est la ligne à haute tension située sur le lac Pontchatrain, près de la Nouvelle-Orléans. En se mettant dans son axe, on peut la voir clairement plonger sous l’horizon en suivant une courbure. Or, les pylônes sont tous à la même hauteur, plantés de façon rectiligne et de niveau. Dans le cas d’une terre plate, les plus lointains devraient sembler plus petits mais être visibles en entier. Or, seule leur partie supérieure est visible, le bas étant sous l’horizon. De même, la ligne qu’ils forment vers l’horizon devrait être droite et non incurvée. Cette courbure, c’est celle de notre planète ! Il serait compliqué de trouver de telle construction dans l’antiquité, mais le raisonnement est simple. |
II°/ Astronomie : c’est la terre ou le soleil qui est au centre de l’univers ?
L’astronomie, qui est l’observation du ciel, est considérée comme la plus ancienne des sciences.
a°/ La préhistoire : avant 4800 av. J.-C.
| Lever et coucher du Soleil, aspect du ciel différent en été et en hiver, position changeante du lever de Soleil par rapport aux étoiles… À sa naissance, l’astronomie sert principalement à mesurer le temps, définit les journées et marque les saisons.
Ci-contre : Représentation d’un aurochs, ancêtre bovin, avec six étoiles des Pléiades au-dessus de lui dans la grotte de Lascaux (entre 17500 et 13000 av. J.-C.). |
 |
b°/ Le Néolithique : entre 4800 av. J.-C. et 2100 av. J.-C.
| Les mégalithes du Néolithique sont constitués d’une ou plusieurs pierres de grande taille érigées sans mortier ni ciment. Ils auraient un rôle multiple : social et culturel, mais aussi astronomique.
Par exemple, sur le site de Nabta Playa en Égypte (4500 à 4000 av. J.-C.), on trouve un cercle de pierres de deux mètres de hauteur. Quatre couples de rocs plus grands forment comme des “portes” sur ce cercle. Deux d’entre elles sont alignées avec l’axe nord-sud, tandis que les deux autres forment une ligne à 70° avec l’est-nord-est… Cette dernière direction est alignée avec la position du lever du Soleil au solstice d’été il y a 6 000 ans, un événement qui marquait le début de la saison des pluies dans le désert. D’après les archéoastronomes, Nabta Playa serait donc, comme d’autres mégalithes du Néolithique, un “observatoire ancien”. |
 |
| Le monument préhistorique de Stonehenge a longtemps été étudié pour ses liens éventuels avec l’astronomie ancienne. Des archéoastronomes ont prétendu que Stonehenge représentait un « ancien observatoire », bien que son utilisation à cette fin soit contestée. Beaucoup pensent également que le site peut avoir eu une valeur astrologique ou spirituelle.
Ci-contre : Mégalithe de Stonehenge (3500 à 3000 av. J.-C.), “observatoire ancien” en Angleterre. |
 |
c°/ Mésopotamie : entre 5300 av. J.-C. et 539 av. J.-C.
| Les Sumériens, les Babyloniens (au sud) puis les Assyriens (au nord) ont peuplé la Mésopotamie (Irak actuel). Ils se distinguent par un développement très poussé des mathématiques.
Ils sont à l’origine des premiers modèles mathématiques de description et de prédiction des phénomènes célestes. Les astronomes connaissent notamment bien les mouvements des planètes visibles à l’œil nu : Mercure, Vénus, Mars, Jupiter et Saturne. Par ailleurs, les savants mésopotamiens inventent les constellations les plus anciennes comme le Lion, le Taureau, le Scorpion et le Capricorne. Ils divisent également la voûte céleste entre douze signes du Zodiaque. Ces premières constellations seront ensuite complétées par les Grecs, qui introduiront des références à leur propre mythologie. Ci-contre : Tablette relatant des observations de Vénus, Ninive (ville d’Assyrie), VIIe siècle av. J.-C. |
 |
d°/ Égypte : vers 2500 av. J.-C.
| Les Égyptiens sont eux à l’origine du calendrier solaire. Ils remarquent que l’apparition de l’étoile Sirius au-dessus de l’horizon terrestre à l’aube, après une période où elle était cachée, se produit approximativement tous les 365 jours, et divisent donc l’année de cette manière. Le cycle de la Lune durant environ 30 jours et nuits, ils divisent l’année en douze mois de 30 jours. Les Égyptiens sont aussi à l’origine du découpage de la journée en 24 heures.
Leurs pyramides sont orientés suivant les quatre points cardinaux, parfois avec une précision impressionnante comme les pyramides de Gizeh. Ci-contre : Une horloge stellaire égyptienne. |
 |
e°/ Grèce : VIIe siècle av. J.-C.
Les connaissances babyloniennes et égyptiennes sont transmises aux savants grecs. Et c’est en Grèce que tout change. Alors que les civilisations mésopotamienne et égyptienne se limitent à la description des phénomènes célestes, les Grecs s’intéressent au “pourquoi”. Ils vont plus loin dans l’analyse en cherchant à déterminer les lois physiques à l’origine du mouvement des astres et à trouver une explication rationnelle à la création du monde.
Deux visions de notre galaxie s’affrontent alors au cours des âges. Le géocentrisme qui place la terre au centre de l’univers et l’héliocentrisme pour qui c’est le soleil.
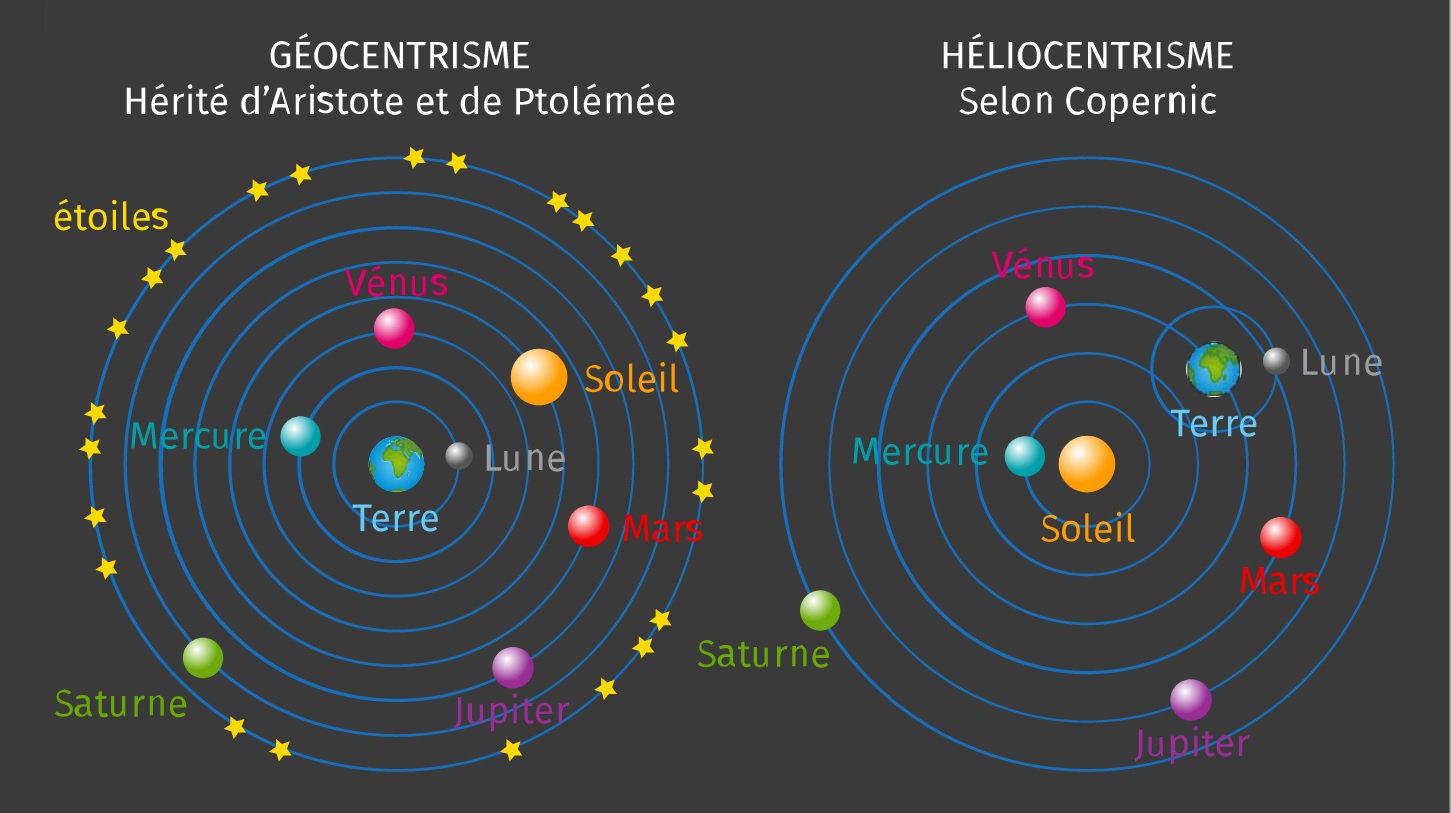
Aristote : Géocentriste. Philosophe grec né en 384 avant JC et mort en 322 avant JC. Il avait une vision géocentrique de l’Univers. Il considérait que la Terre est fixe au centre de l’univers et que tous les astres tournent autour d’elle selon des trajectoires circulaires.
| Cette idée permettait d’expliquer grossièrement les mouvements apparents de la Lune et du Soleil, qui sont à peu près réguliers, mais elle ne pouvait pas justifier la complexité du mouvement des planètes qui parcourent la voûte céleste en effectuant des boucles. Par exemple, voici la trajectoire de Mars (la courbe blanche). On observe que Mars semble revenir en arrière et forme une boucle. Cette hypothèse n’expliquait pas non plus les grandes variations de l’éclat lumineux des planètes. | 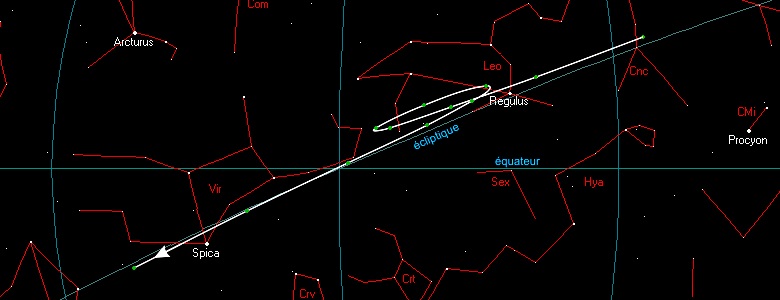 |
|
Position et phases changeantes de la Lune au-dessus des sommets du Groupe de Cridola, dans les Alpes italiennes, au cours d’un mois lunaire, appelé mois synodique. |
Il est à noter que la forme des galaxie varie au cours du temps. |
Ptolémée : Géocentriste. Claude Ptolémée, communément appelé Ptolémée, était un astronome (et astrologue), probablement d’origine grecque, qui vivait à Alexandrie en Égypte au 2ième siècle.
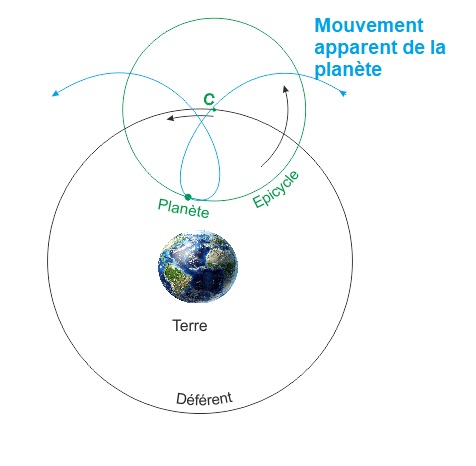
| Pour rendre compte de ces aspects, Ptolémée a proposé une modification au modèle d’Aristote.
Il a conservé la position centrale et fixe de la Terre mais chaque planète tournait cette fois autour d’un point qui suit la trajectoire circulaire d’Aristote. Ainsi chaque planète effectuait un petit cercle nommé épicycle dont le centre se déplaçait sur le déférent. Cette disposition décrivait mieux les trajets des planètes et elle expliquait aussi les variations d’éclats par des variations de distances. |
 |
f°/ Europe : XVIe siècle.
C’est le système de Ptolémée qui restera en vigueur jusqu’au XVIe siècle.
Copernic : Héliocentriste. Nicolas Copernic était un chanoine, médecin et astronome polonais né à Thorn en 1473 et mort à Frauenburg en 1543.
| Copernic était conscient des insuffisances du système de Ptolémée et il l’a reconsidéré en mettant le Soleil au centre de l’Univers.
Il n’était certainement pas le premier à y avoir pensé mais, à cette époque on craignait la censure (et la répression) des autorités religieuses. Or l’idée de chasser la Terre (et l’homme) du centre de l’Univers était mal perçue par la communauté religieuse. Copernic a exposé son système planétaire dans son ouvrage « De Revolutionibus Orbium Coelestium » qui a été imprimé juste avant sa mort en 1543. Cependant, son système il n’explique pas mieux les irrégularités de la marche des planètes dans le ciel, et lui aussi fait appel à des épicycles et des excentriques. |
 |
Tycho Brahé : Géocentriste. Astronome Danois né à Knudstrup en 1546 et mort à Prague en 1601.
| Il était opposé aux thèses héliocentriques de Copernic et préférait considérer la Terre fixe au centre de l’Univers. En fait, il croyait que les planètes tournaient autour du Soleil et que celui-ci tournait autour de nous avec tout ce cortège. C’était une sorte de compromis entre le système d’Aristote et celui de Copernic.
Cependant, Tycho Brahé était un observateur et il avait besoin d’un mathématicien pour exploiter ses mesures. Ceci le conduisit à rechercher la participation de Kepler. C’est en 1600, que l’astronome et mathématicien Kepler rencontra Brahé et devint son collaborateur. Quelques mois plus tard, la mort emporta Tycho Brahé et Kepler récupéra une partie de ses observations. |
 |
Kepler : Héliocentriste. Johannes Kepler (1571 – 1630) a alors étudié les mesures de Tycho Brahé dans le but de comprendre les mouvements des planètes.
| C’est de l’étude des positions de la planète Mars que la solution a commencé à germer dans l’esprit de Kepler.
En 1609, Kepler publia un livre intitulé « Astronomia nova » (Astronomie nouvelle) dans lequel il exposait les deux premières lois que l’histoire des sciences a attachées à son nom. Neuf années plus tard, en 1618, il énonça sa troisième loi. |
 |
Newton : Isaac Newton (
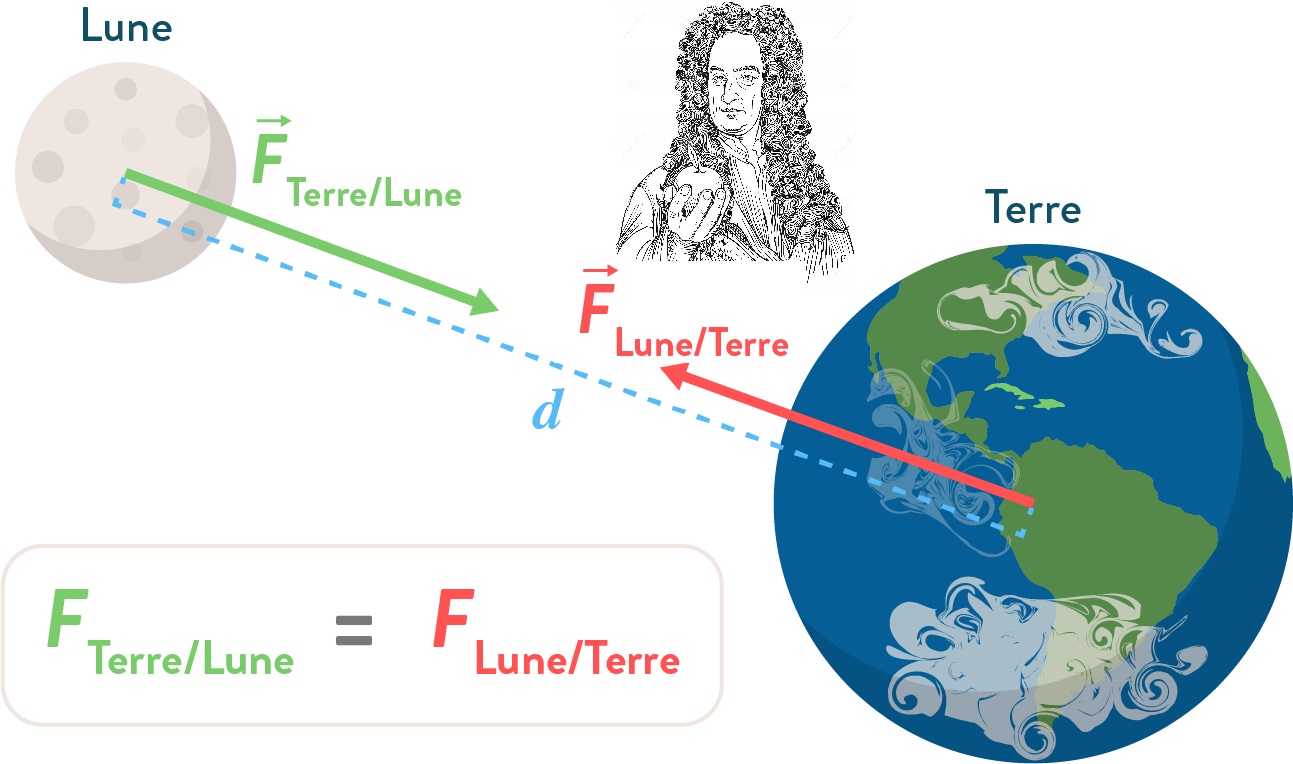
| Les lois de Kepler étaient déduites des observations, celles Newton sont des hypothèses sur la réalité physique des relations entre matière, forces et mouvements.
Premier principe de Newton :Tout corps persiste dans son état de repos, ou de mouvement uniforme en ligne droite, à moins que des forces exercées sur lui ne l’obligent à changer cet état. |
 |
III°/ Circonférence de la terre et distance terre – lune – soleil :
Comment mesurer des distances inaccessibles, qui plus est sans avoir une idée précise de notre galaxie ? Et bien les savant Grecs de l’antiquité l’on fait …
La chronologie :
| Date | Savant | Distances calculées | Distances réelles | Erreurs |
| -280 ans av. J.C. | Aristarque de Samos | Terre-lune = 495 338 km | Terre-lune = 384 400 km | + 28,86 % |
| -200 ans av. J.C. | Ératosthène | Terre-soleil = 7 344 854 km | Terre-soleil = 149 597 870 km | – 49 % |
| -200 ans av. J.C. | Ératosthène | Rayon terre = 6 484 km | Rayon terre = 6 371 km | + 1,74 % |
| -167 ans av J.C. | Hipparque de Nicée | Terre-lune = 424 309 km | Terre-lune = 384 400 km | + 10,4 % |
| 1751 | Le Monnier | Terre-lune = 382 542 km | Terre-lune = 384 400 km | – 0,48 % |
| 1969 | Saturne 5 | Terre-lune = 384 400 km | Terre-lune = 384 400 km | 0 % |
a°/ Ératosthène et la circonférence de la terre :
Nous connaissons la circonférence de la terre, qui est de 40 075 Km grâce aux satellites qui gravitent autour de nous.
Mais le plus extraordinaire, est que 3 siècles avant J.C. Ératosthène, sans satellite ni aucun instruments modernes, a été capable d’en donner une valeur incroyablement précise.
Ses calculs lui on permis de donner une circonférence 39 438,20 km soit une erreur de moins de 2%.
3 siècles avant J.C., Ératosthène se promenait à la fin du mois de juin à Syène au sud de l’Égypte, sous le tropique du Cancer. Le jour du solstice d’été, à midi (les rayons du soleil sont alors parallèles à l’équateur), il regarde au fond d’un puits. Il constate qu’il n’y a pas d’ombre à l’intérieur, et note ce phénomène. L’année suivante, à la même date et à la même heure, il est à Alexandrie au nord de l’Égypte qui se trouve à 780 km (les distance étaient mesurer en stade à l’époque). Il regarde dans un puits et constate, avec surprise, qu’il y a de l’ombre. Les rayons du soleil ne serait-il pas parallèles au nord et au sud ?
Cette hypothèse est peu probable, compte tenu de la distance terre-soleil. Faisons plutôt, pense-t-il, l’hypothèse que ce sont les puits qui ne sont pas parallèles.
Donc, si les puits sont bien fait et qu’ils sont perpendiculaires au sol, c’est la terre qui est ronde et l’axe des puits forment entre eux un angle a° de 7,12°.
Ératosthène était un astronome et mathématicien grec qui a vécu environ 200 ans avant Jésus Christ. Il a réussi à calculer le périmètre de la terre, avec une belle précision, ce qui est une sacrée performance pour l’époque.
Il constata qu’au solstice d’été à midi (les rayons du soleil sont alors parallèles à l’équateur), le soleil éclairait le fond d’un puits de la ville de SYENE (S) au sud de l’Égypte, sous le tropique du Cancer. En même temps à ALEXANDRIE (A), située à 800 km plus au nord de SYENE et sur le même méridien, un obélisque projetait une ombre qui faisait un angle de 7,12°.
Les rayons du soleil ne serait-il pas parallèles au nord et au sud ? Cette hypothèse est peu probable, compte tenu de la distance terre-soleil. Faisons plutôt, pense-t-il, l’hypothèse que ce sont les puits qui ne sont pas parallèles.
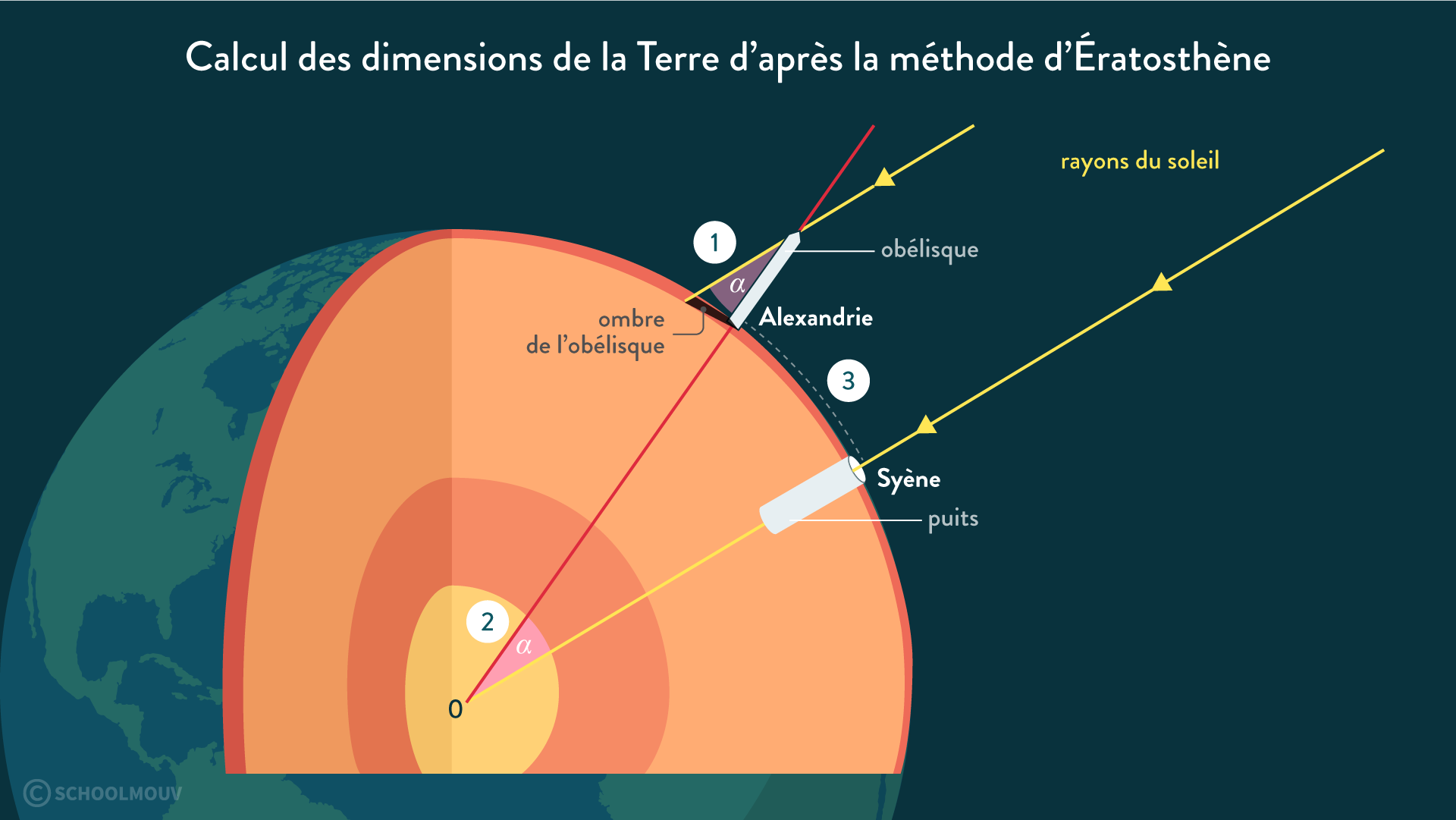 |
Distance ALEXANDRIE-SYENE AS = 780 km et a° = 7,12° :
360° ? Circonférence de la terre Ct a° ? AS Donc : Ct = (360 x AS)/ a Ct = (360 x 780) / 7,12 Ct = 39 438,20 km La circonférence réelle de la terre est de 40 075 km. Ératosthène a donc commis une erreur de 1,6%, ce qui est une immense performance. |
b°/ Calcul de la distance terre-lune : Par Aristarque de samos (-310 -230 avt. JC)
La distance terre-lune est de 384 400 km. Nous avons des outils moderne et précis pour effectuer cette mesure, mais les Grecs, deux siècles avant Jésus Christ ont été capables d’obtenir de très belles approximations.
 |
 |
|
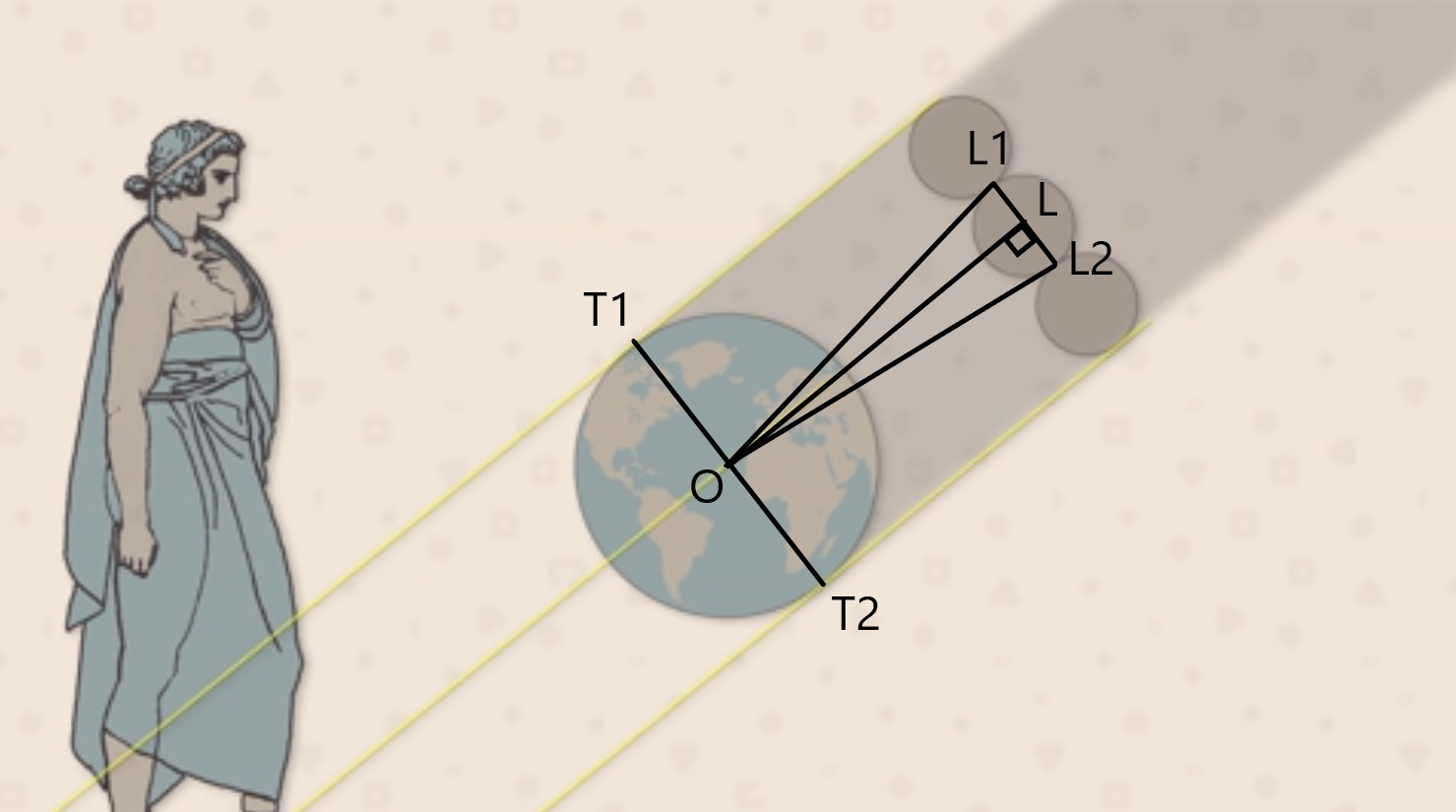
Lors d’une éclipse de Lune (passage de la Lune dans l’ombre de la Terre), Aristarque de samos (-310 -230 avt. JC) remarqua que l’éclipse avait durée 4 heures et que l’on pouvait mettre 3 lunes dans l’ombre de la terre. Rayon_{Lune} = \frac{2\times Rayon_{Terre} }{6} = \frac{6484}{3} = 2161 \ km Le rayon réel de la lune étant de 1737,4 km l’erreur est seulement de 24%. Aristarque a considéré que le soleil était à l’infini et que l’ombre faite par la terre était un cylindre, alors que c’est un cône. Malgré tout, il a été capable de mesurer des distances inatteignables. |
Il détermine que \widehat{L_{1}OL_{2}} mesure un demi degrés. Sachant que le rayon terre d’après Ératosthène fait 6 484 km.
tan \widehat{LOL_{2}}=\frac{opp \widehat{LOL_{2}}}{adj \widehat{LOL_{2}}}=\frac{LL_{2}}{OL} \ donc \ OL = \frac{LL_{2}}{tan \widehat{LOL_{2}} } = \frac{T_{1}T_{2}}{6 \times tan 0,25} \\ OL = 38,2 \times T_{1}T_{2}= 495 378 \ km La distance réelle terre-lune étant de 384 400 km, l’erreur est de 28,87 %, ce qui est très correct car la mesure de 0,5° durant l’antiquité s’avère difficile (certain ont suggéré que Aristarque aurait plutôt mesuré 2°. L’erreur serait alors de 84% !!!). |
|
Périmètre Révolution lune = 2 \pi R donc : Distanceterre-lune = \frac{2 \ 334\ 240}{2\pi }= 371 \ 505,8\ km
Soit une erreur de seulement 3,35 %, ce qui est très superbe comme précision. Bien que les Grecs utilisaient le cadran solaire ou la clepsydre, leur mesure du temps était tout à fait correcte. |
Remarque : comment mesurer l’angle \widehat{L_{1}OL_{2}} ?
 |
Il suffit de viser l’objet inatteignable avec une pièce de monnaie par exemple dont on connait le diamètre. L’angle de visée est alors facilement mesurable. Bien entendu l’erreur de mesure n’est pas négligeable. |
c°/ Calcul de la distance terre-soleil :
Aristarque c’est aussi essayé au calcul de la distance terre-soleil. Mais sa mesure d’angle c’est révélé bien trop inexacte.
 |
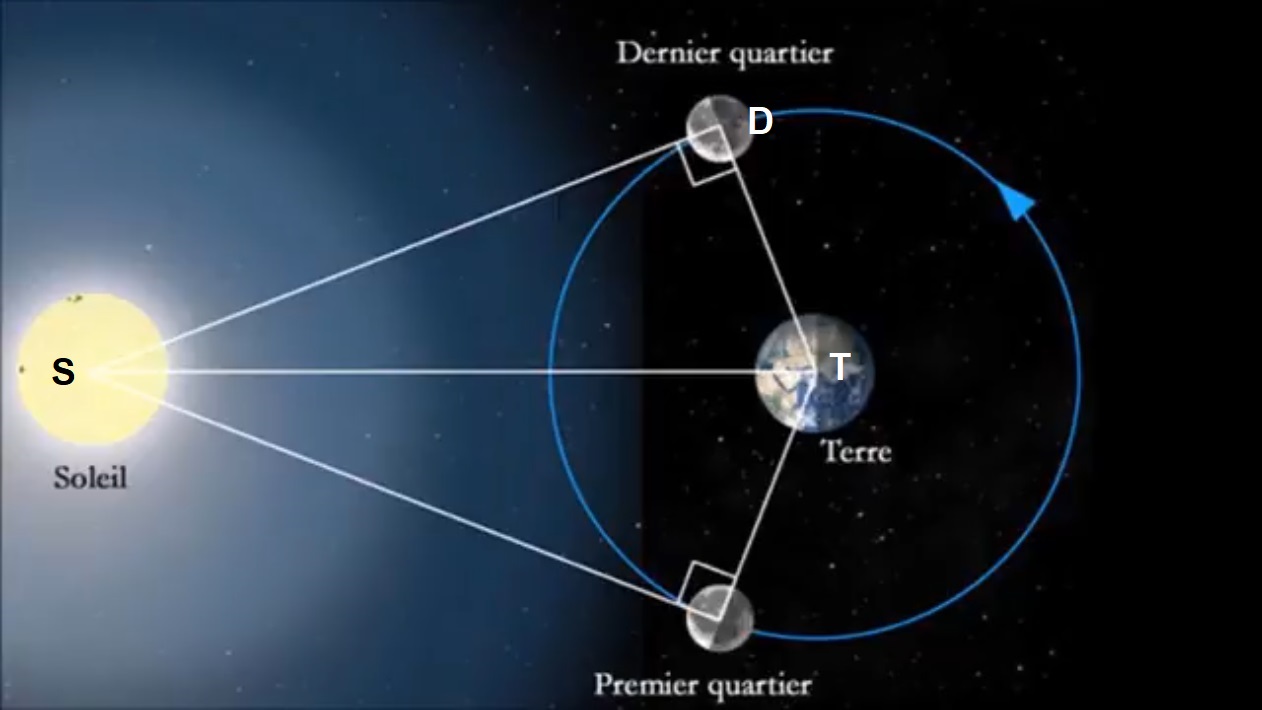 |
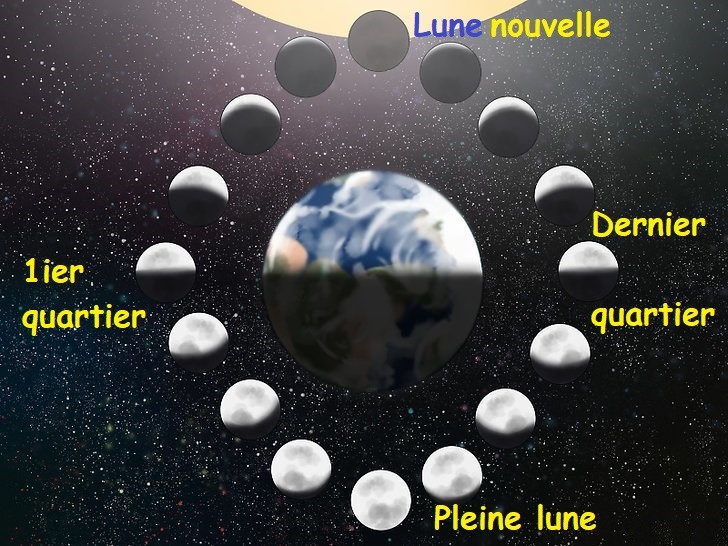
| Lorsque la lune se présente sous différents aspects car elle réfléchit la lumière du soleil.
Au premier et au dernier quart, la lune présente une ombre qui la coupe exactement en deux. Soleil, terre et lune s’inscrivent alors dans un triangle rectangle. Aristarque avait mesurer un angle \widehat{DST} de 3°. La mesure du temps était moins facile et précise que maintenant. |
Dans le triangle DST rectangle en D
sin \widehat{DST}=\frac{opp \widehat{DST}}{hypo} = \frac{DT}{ST} \ donc \ : \ ST = \frac{DT}{sin \widehat{DST}}= \frac{371 \ 505,8}{sin \ 3} = 7 \ 098\ 481,17 \ km La distance terre-soleil est de 149 597 870,7 km, l’erreur est donc considérable mais le raisonnement est correct. En fait l’angle est de 0,15° : ST = \frac{DT}{sin \widehat{DST}}= \frac{371 \ 505,8}{sin \ 0.15} = 141 \ 904\ 619 \ km |
IV°/ Le tunnel de Samos :
550 ans avant Jésus Christ, sur l’île grecque de Samos (là où serait né Pythagore), Polycrate (un tyran de l’île) décida de faire creuser un tunnel qui aurait pour but de ravitailler sa ville en eau sans que cet approvisionnement ne puisse être facilement coupé en cas de siège. Ce tunnel se présenterait alors sous la forme d’un aqueduc souterrain et devrait traverser un petit mont (le Mont Kastro) sous l’Acropole de Samos sur une longueur d’environ 1km. L’aqueduc puiserait sa source de l’autre côté de la montagne. De plus, il devrait être quasi-horizontal afin de permettre l’écoulement naturel des eaux jusqu’à la ville.
C’est Eupalinos de Mégare (fils de Naustrophus et élève de Pythagore) qui fut désigné comme architecte-ingénieur de l’ouvrage. Celui-ci, afin de gagner du temps, demanda à deux équipes de creuser simultanément des deux côtés de la montagne. Il ne lui fallut tout de même pas moins de 10 ans pour parvenir à ses fins.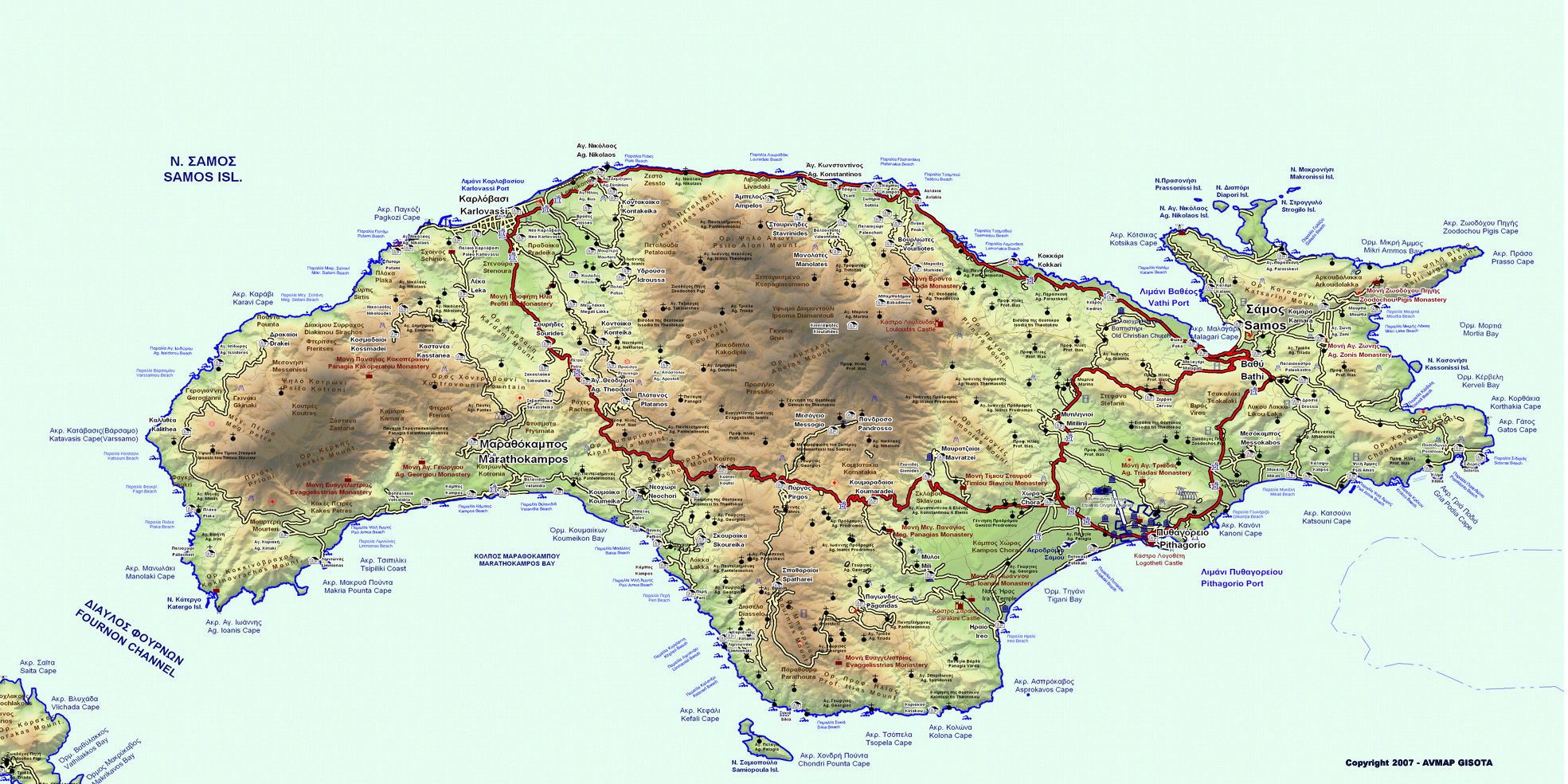
| Visiter le tunnel | Visiter le tunnel |
Aujourd’hui, même si on ne sait toujours pas exactement comment Eupalinos réalisa ses plans et que bon nombre d’hypothèses circulent, on peut être sûr qu’il fut confronté à 3 problèmes :
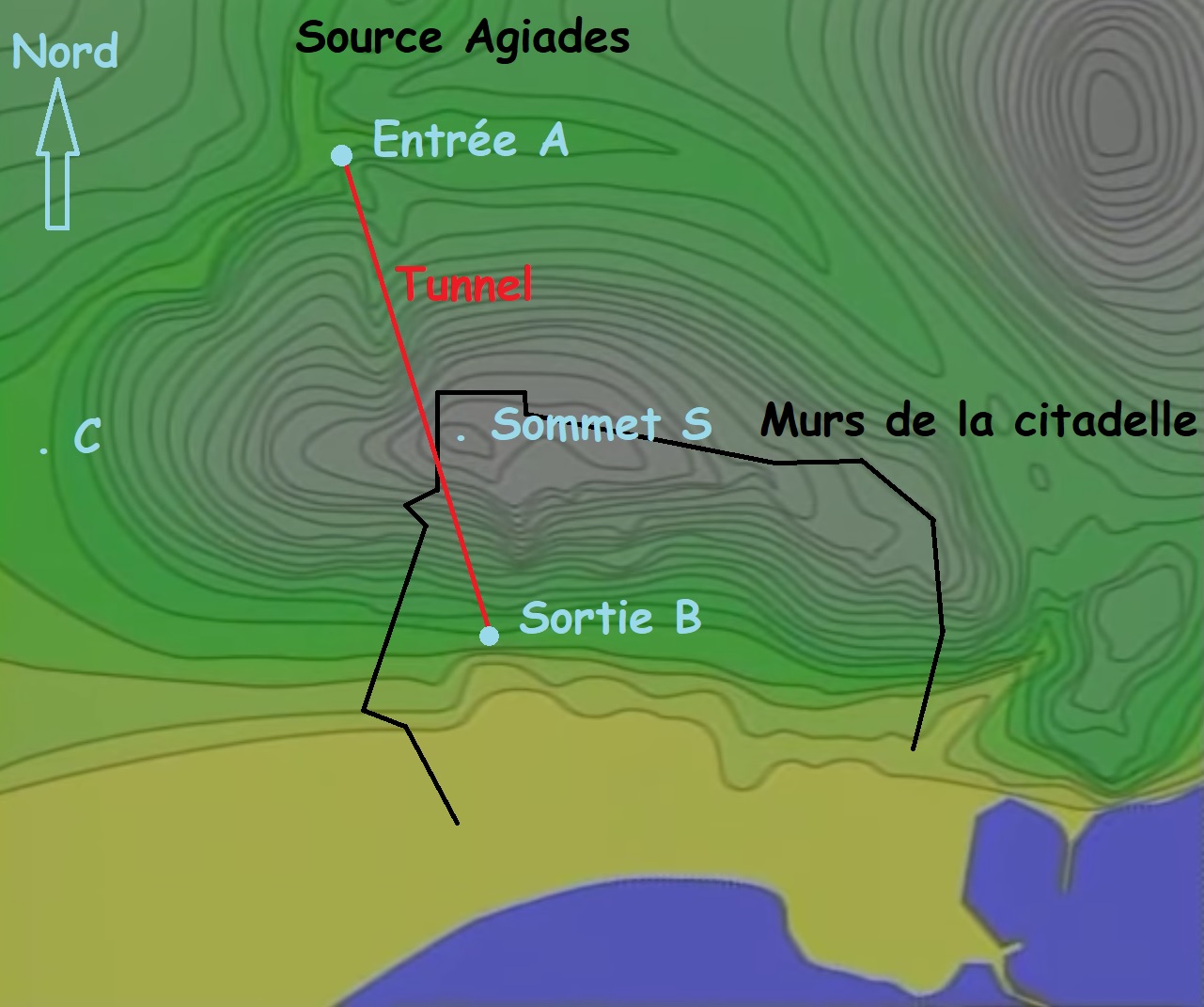
1/ Garder l’aqueduc horizontal, avec une légère pente entre l’entrée et la sortie pour permettre l’écoulement de l’eau.
 |
 |
C’est le problème le plus important. Déterminer l’entrée A et la sortie B du tunnel. Pour cela il suffit de choisir l’endroit de la sortie B pour qu’elle surplombe la ville et de contourner la montagne par l’ouest en suivant la même courbe de niveau, en passant par le point C et rejoindre l’entrée A.
Des preuves archéologiques nous montrent que les Samiens disposaient d’instruments pour déterminer l’horizontale : des sortes de gouttières en terre cuite, posées sur des pieux, dans lesquelles on versait de l’eau. L’horizontale était obtenue quand celle-ci ne s’écoulait pas. Cependant, si les gouttières mesuraient 2 m de long, il en aurait fallu environ 1100, car la distance séparant l’entrée A de la sortie B, en passant par l’ouest, est de 2200 mètres.
Les Samiens utilisèrent alors une petite astuce, leur permettant de réduire considérablement le nombre de pieux à planter. En effet, ils commencèrent par planter deux pieux A et B distants l’un de l’autre d’environ 10 mètres, dont les sommets étaient à même niveau en utilisant la méthode des gouttières. Ils alignaient ensuite un pieu C à environ 100 mètres, en utilisant des visées oculaires et grâce aux deux autres pieux préalablement mis en place.
 |
 |
2/ Les 2 équipes ne doivent pas se rater, car partant de chaque côté, le risque de ne pas se rencontrer était grand. Il faut bien déterminer l’orientation dans laquelle le tunnel doit être percé.
Deux méthodes furent imaginées, car nous n’avons aucun indice sur la façon exacte qui fut utilisée.
La première méthode : celle des pieux
Comme l’entrée A est invisible de la sortie B du tunnel à cause de la montagne, il suffirait de construire une tour au sommet S, visible de A et de B. En disposant des pieux intermédiaires entre les extrémités A et B et le sommet S, il est possible de réaliser un alignement de pieux entre A et B. On vérifie cet alignement comme précédemment, de proche en proche.
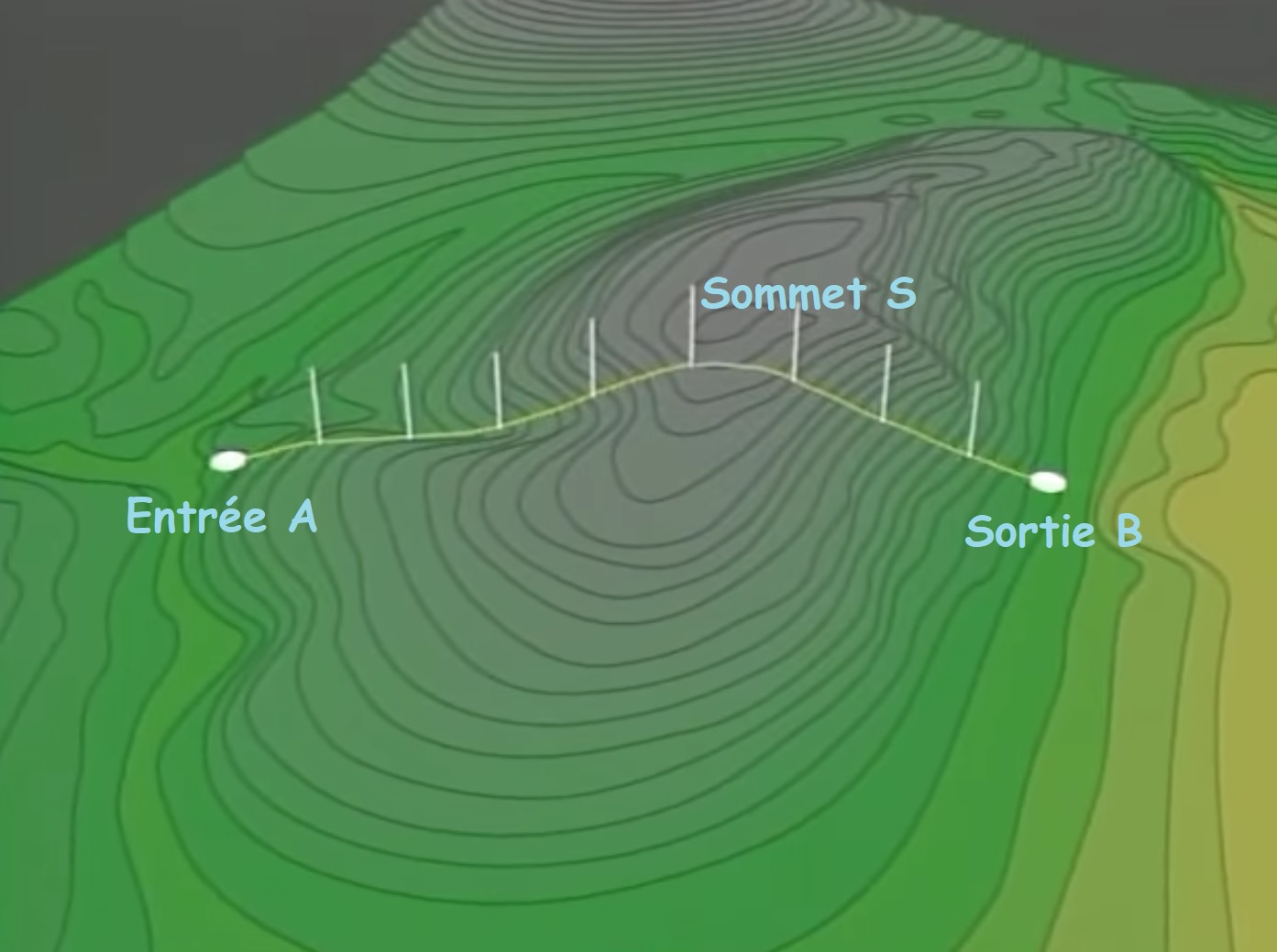
Une autre méthode a été proposée, celle de Héron d’Alexandrie.
Elle consiste à rester sur le même niveau et à relier l’entrée A et la sortie B du tunnel à l’aide de planche que l’on dispose toujours en ligne droite ou à angle droit. Ainsi il suffit de compter le nombre de planches disposées vers l’ouest (de B vers 6, de 5 vers 4 …) et vers le nord (de 6 vers 5, de 4 vers 3 …). On détermine ainsi un triangle ABC rectangle en C dont on connait AC (la longueur des planches dirigées vers le nord) et BC (la longueur des planches dirigées vers le l’ouest entre B et C). On peut ainsi calculer la longueur AB du tunnel, mais surtout fabriquer deux autres triangles rectangles AFG et BED, semblables à ABC.
Pour cela il suffit de faire en sorte que (BD) soit perpendiculaire à (BC) ainsi que (AG) et (FG), et que les longueurs des triangles AFG et BED soient des réductions de ABC, d’un rapport que l’on pourra choisir à notre convenance. L’axe (EB) sera ainsi orienté de la même façon que l’axe (AF) et surtout que l’axe (AB) du tunnel.
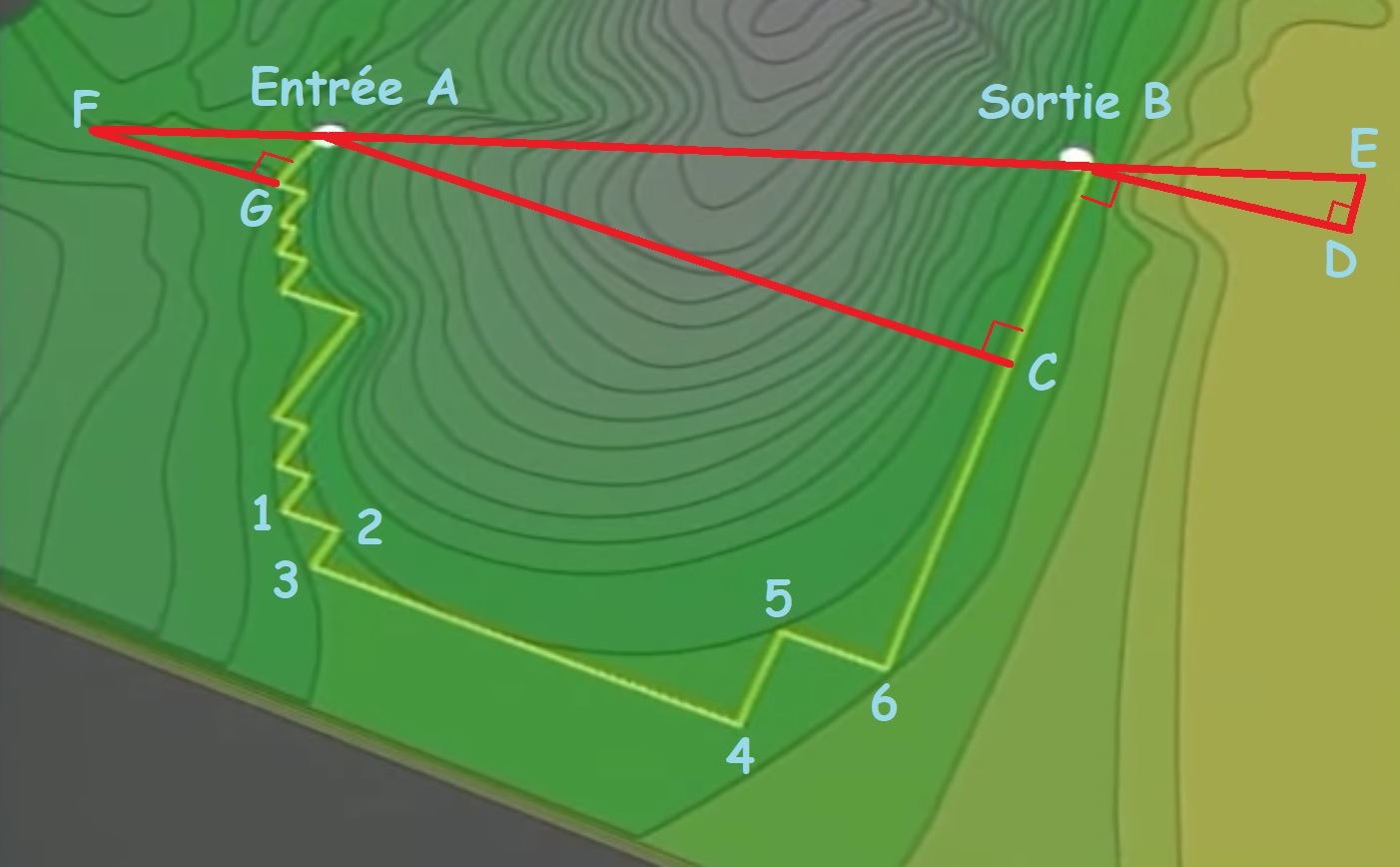
Les deux équipes connaissent à présent l’endroit où commencer à creuser et la direction à suivre.
3/ La longueur du tunnel. Estimer la longueur du tunnel. Peut important sauf pour prévoir le temps et le coût financier du chantier.
La longueur de l’hypoténuse AB du triangle rectangle ABC précédent.
Pour conclure, il est intéressant de noter que le tracé réel du tunnel n’est pas parfaitement rectiligne. Il présente quelques zigzags au milieu du parcours. Il faut tenir compte des erreurs de précision des mesures, du manque d’outils et des erreurs humaines.
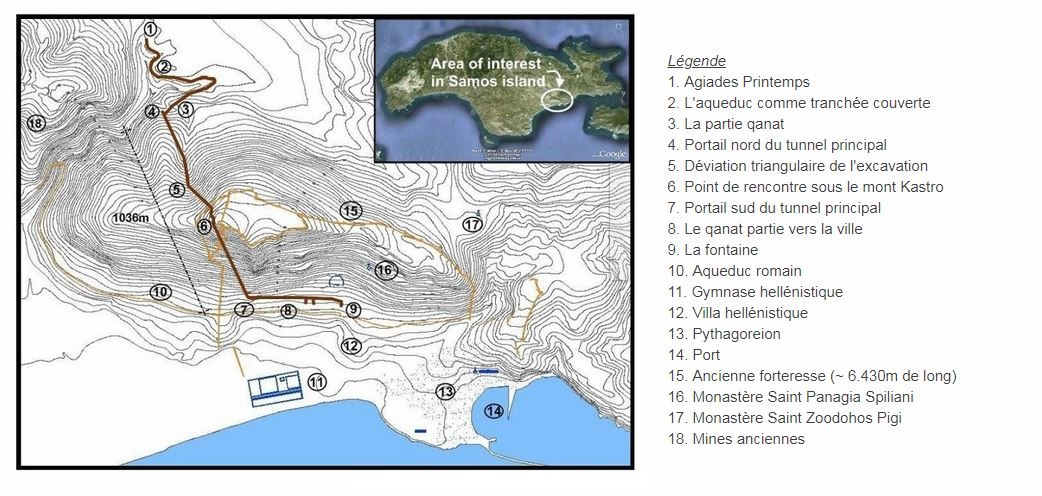 |
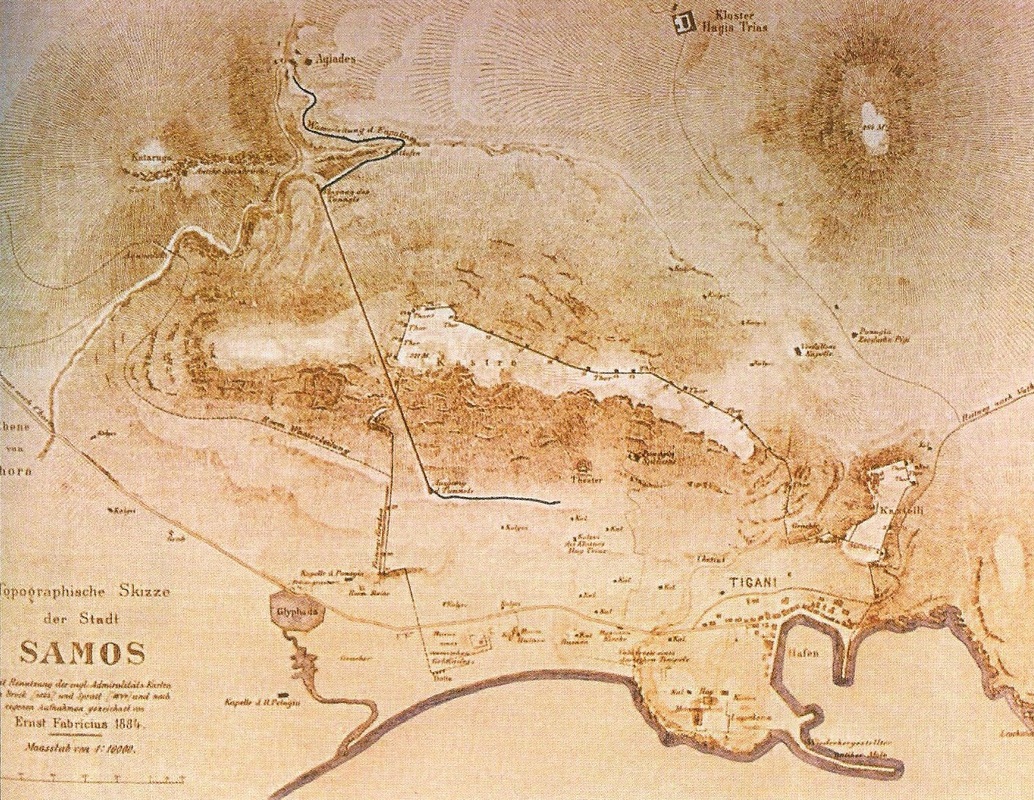
Carte de Ernst Fabricius (1884) |
Victor Guerin, archéologue français à la recherche de la « grande source » d’Hérodote, fut le premier à découvrir les 400 premiers mètres de l’aqueduc, à partir de la source des Agiades, en 1853. Cependant, ce fut le moine Kyrillos Moninas, en 1882, du monastère voisin d’Agia Triada, qui a réussi à découvrir les entrées sud et nord du tunnel principal. En 1884, E. Fabricius, archéologue de l’Institut archéologique allemand d’Athènes (DAI), visita l’île et inspecta le tunnel jusqu’au point qui pouvait être visité à l’époque. En 1971, U. Jantzen, directeur du DAI, réussit après de longs préparatifs, à dégager complètement le tunnel (1971-1973).
V°/ Poids des planètes :
a°/ La constante gravitationnelle G : Newton et l’expérience de Henry Cavendish au XVIIIième siècle
En physique, la constante gravitationnelle, aussi connue comme la constante universelle de gravitation, notée G, est la constante de proportionnalité de la loi universelle de la gravitation d’Isaac Newton. Cette constante physique fondamentale apparaît dans des lois de l’astronomie classique qui en découlent (gravité à la surface d’un corps céleste, troisième loi de Kepler, etc.), ainsi que dans la théorie de la relativité générale d’Albert Einstein.
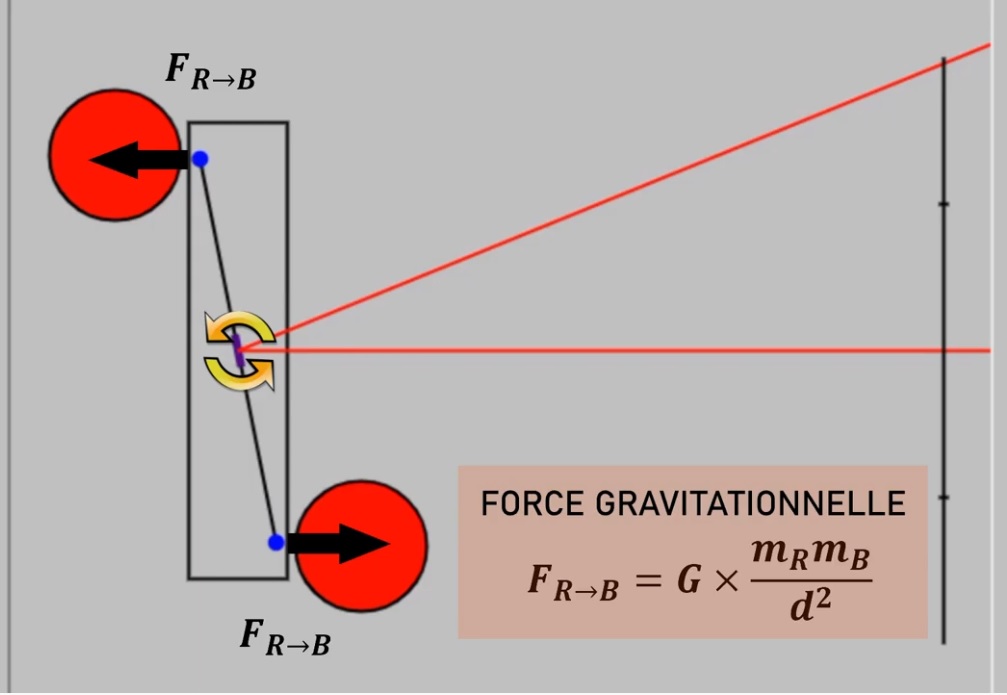
Newton a établit une loi qui explique que 2 corps s’attirent mutuellement, proportionnellement au produit des deux masses m1 et m2, et inversement proportionnellement au carré de la distance d qui les sépare. F_{1\to 2}=F_{2\to 1}= G \times \frac{m_{1}m_{2}}{d^{2}}.
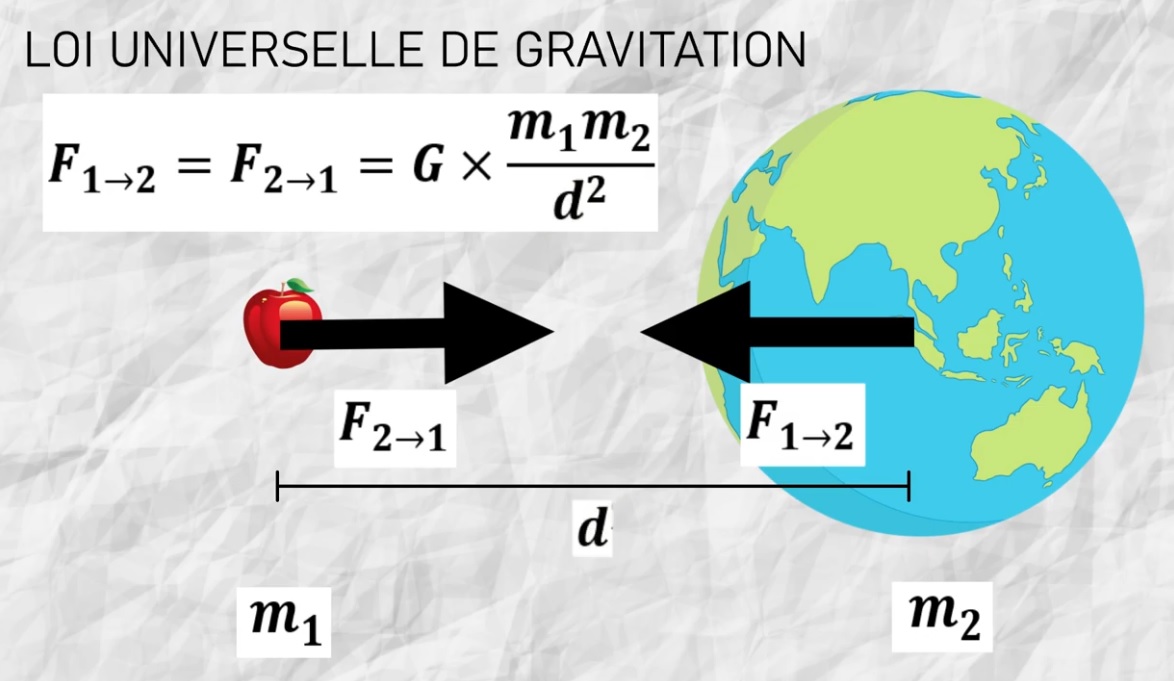 |
 |
|
Loi universelle de la gravitation selon Newton. |
Expérience de Cavendish. On connait les masse mB des boules bleues et mR des boules rouges, la distance d entre les boules et la force de traction F_{R\to B} des boules rouges sur les bleues. On peut donc calculer la constante G.
G = 6,674184 10–11 m3 kg–1 s–2 |
b°/ Les 3 lois de Kepler :
Kepler (
Les 3 lois de Kepler :
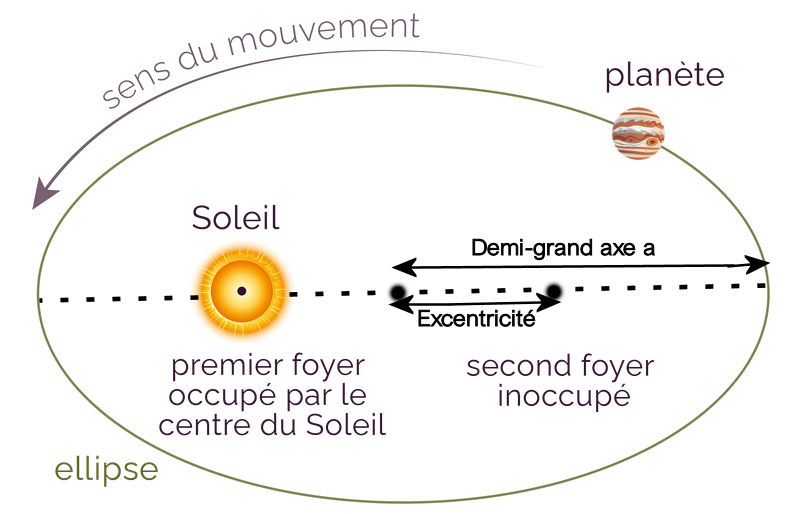
| 1ière loi : Loi des orbites
Les planètes tournent autour du Soleil en décrivant des ellipses dont le soleil occupe un des foyers. On appellera a le demi grand axe de cette ellipse et T la période orbitale de cette planète autour du soleil. Les planètes de notre système solaire ont une trajectoire presque circulaire car leur excentricité (distance centre – 2ième foyer) est très faible. |
 |
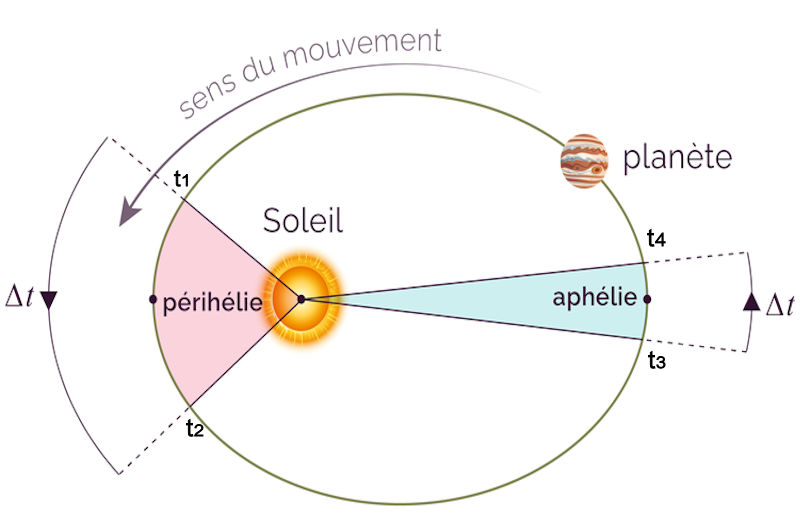
| 2ième loi : La loi des aires
Durant un temps donné, la surface balayée par la planète et la même. Donc, plus une planète est proche du soleil plus sa vitesse augmente. Entre t1 et t2 la surface bleue de l’ellipse et la même que entre t3 et t4. |
 |
| 3ième loi : Loi des périodes
Les carrés des périodes de révolution des planètes sont proportionnels aux cubes des grands axes de leurs orbites. |
\huge \frac{a^{3}}{T^{2}} = k |
Démonstration de la 3ième loi de Kepler :
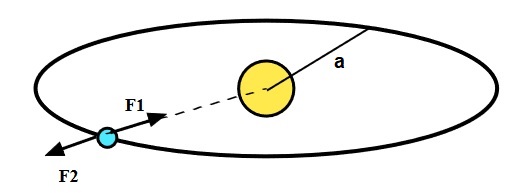
Si un objet de masse m tourne autour d’un autre de masse M infiniment plus grand (les planètes autour du soleil, la lune autour de la terre ou un satellite autour d’un planète) alors il subit deux forces opposées qui se compensent :
| – Une force d’attraction : Force de gravitation universelle \huge F_{1} = \frac{GmM}{a^{2}}
– Force centrifuge due à la rotation de la terre autour du soleil \huge F_{2} = \frac{mV^{2}}{a} |
 |
G = constante gravitationnelle = 6,674×10-11 Nm2kg-2
M = masse de l’objet massif = Constante m = masse de l’objet en mouvement autour de M a = longueur du demi-grand axe de la trajectoire elliptique de l’objet m autour de M V = vitesse de la rotation de m autour de M T = période de révolution sidérale en seconde |
c°/ Cas de la terre :
G = constante gravitationnelle = 6,674×10-11 Nm2kg-2
m = masse de la terre
M= masse du soleil
a = distance terre soleil = 150×106 km
V = vitesse de la rotation de la terre autour du soleil. V= \frac{2\pi a}{T} = \frac{2\pi \times 1,5 \times10^{11}}{365\times24\times3600} =29 886 \ m/s \simeq 3 \times10^{4} \ m/s
| Puisque les forces F1 t F2 sont égales : \huge F_{1} = F_{2} \\\frac{GmM}{a^{2}} = \frac{mV^{2}}{a} \\M =\frac{aV^{2}}{G} \\M =\frac{1,5 \times 10^{11}\times (3\times10^{4})^{2}}{6,674\times10^{-11}} = 2,02\times 10^{30} kg | G = constante gravitationnelle = 6,674×10-11 Nm2kg-2
m = masse de la terre M= masse du soleil a = distance terre soleil = 150×106 km V = vitesse de la rotation de la terre autour du soleil. V= \frac{2\pi a}{T} = \frac{2\pi \times 1,5 \times10^{11}}{365\times24\times3600} =29 886 \ m/s \simeq 3 \times10^{4} \ m/s |
d°/ Cas des autres planètes :
On peut procéder de la même manière avec les satellites des planètes Jupiter, Mars et Saturne.
VI°/ Vitesse de la lumière :
La vitesse de la lumière est la vitesse maximale que l’on peut atteindre (enfin, jusqu’à preuve du contraire). Elle est de 299 792 458 m/s. Mais très tôt on a su la calculer avec des moyens dérisoires.
L’histoire de la mesure de la vitesse.
Les dates clefs :
| Année | Savants | Technique | Valeur | Erreur | Conclusions |
| (en km/s) | (en %) | ||||
| < 1000 | Alhazen (965–1039) | Réfraction de la lumière dans l’eau : Lorsque l’on plante un bâton dans l’eau on a l’impression qu’il est brisé. Alhazen comprend que cela est due à la vitesse de la lumière qui est différente dans l’air et dans l’eau. | Non concluant |
La lumière a une vitesse mais elle est incalculable pour le moment. |
|
| < 1638 | Galilée (1564–1642) | Lanternes masquées : deux hommes munis d’une lanterne et placés à une distance de 1800 m, font l’expérience suivante : le premier découvre sa lanterne en déclenchant une clepsydre (horloge), le second découvre la sienne dès qu’il aperçoit le signal lumineux et le premier arrête son horloge dès qu’il voit le signal lumineux. Le temps d’aller et retour du signal lumineux peut être ainsi en théorie apprécié. | Non concluant | La lumière paraît être instantanée car la distance est trop courte et il lui faut quelques millionièmes de seconde pour faire les 3,6 kilomètres. Galilée en déduit que la vitesse de la lumière est trop élevée pour être mesurée | |
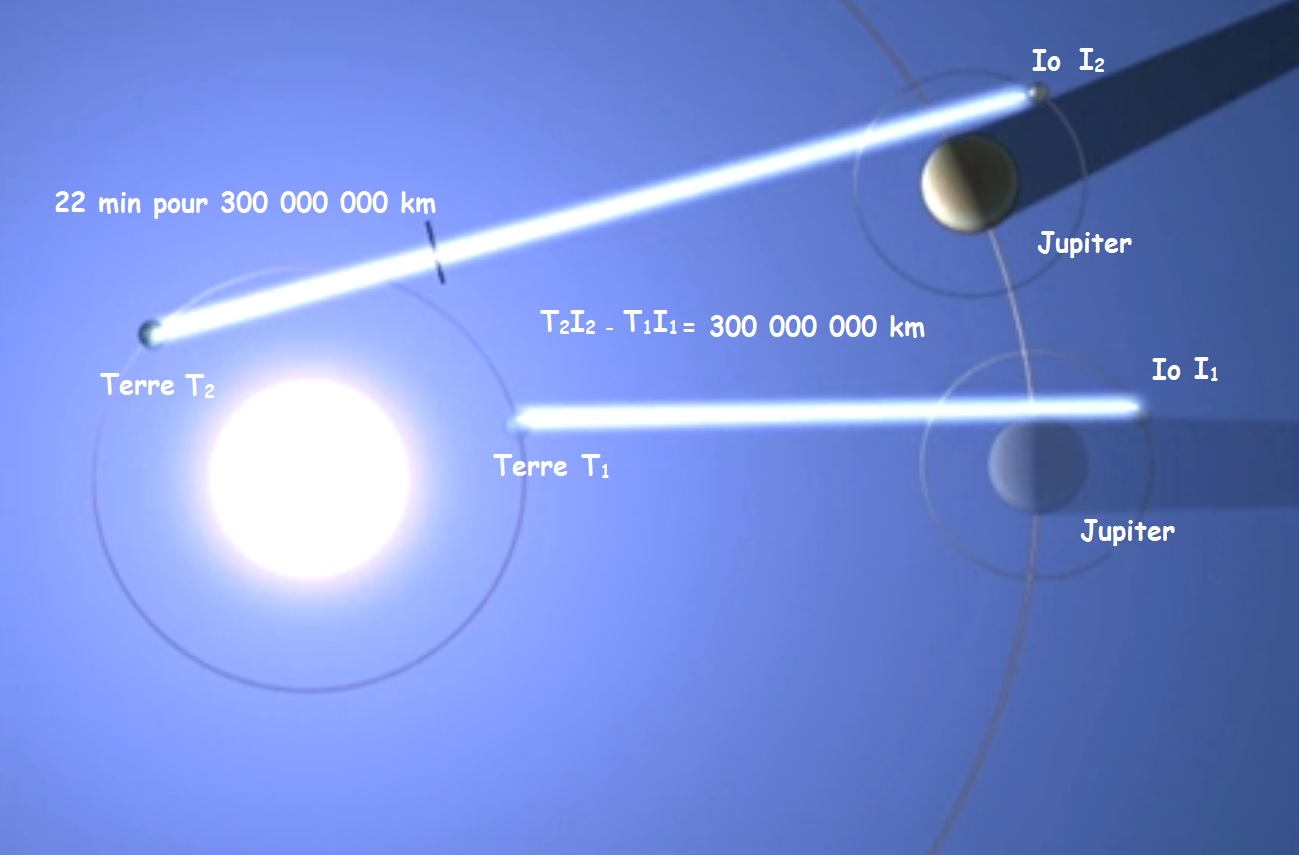
| 1676 | Ole Rømer (1644–1710) et Christiaan Huygens | Observation des lunes de Jupiter : En 1676, Ole Rømer étudie les éclipses d’Io. Ce satellite de Jupiter n’est plus visible lorsqu’il traverse la zone d’ombre de Jupiter. Ces éclipses sont bien connues mais ne respectent bizarrement pas toujours les horaires prévus par les calculs établis par les tables de Cassini. Römer prouve que ces variations ne peuvent correspondre qu’au temps supplémentaire que met la lumière d’Io pour nous parvenir quand Jupiter et elle sont plus éloignées de la Terre : la lumière a donc une très grande vitesse. Il observe qu’il y a 22 min pour pour traverser l’équivalent du diamètre de l’orbite terrestre. | 227 272 | -24,2 % | La distance terre-soleil et le mouvement des astres n’étaient pas très précis à l’époque, mais le raisonnement était exact.
|
| 1729 | James Bradley (1693-1762) | Aberration de la lumière : L’aberration est le fait qu’en raison du mouvement de la Terre autour du Soleil toutes les étoiles effectuent un mouvement annuel apparent, selon une ellipse plus ou moins aplatie selon leur position, dont le demi grand axe est de 20,4 secondes de degré. Si on l’exprime en radians, la moitié de cette amplitude est le rapport entre la vitesse de la Terre sur son orbite et la vitesse de la lumière. Bradley a ainsi estimé que la lumière allait 10 210 fois plus vite que la Terre.
C’était bien mieux que Cassini, mais il restait à estimer avec précision la distance Terre-Soleil pour obtenir une bonne valeur de la vitesse de la lumière. |
301 000 | 0,40 % | V_{Lux}= 10 \ 210 \times V_{Terre} \\ \\ \frac{Distance_{Terre-Soleil}}{T_{Terre-Soleil}}=10 \ 210 \times \frac{2\pi Distance_{Terre-Soleil} }{1 \ an} \\ \\ T_{Terre-Soleil} = \frac{365 \times 24 \times 3600}{10 \ 210 \times 2\pi } = 492 \ secondes = 8 \ min \ 12 s |
| 1849 | Hippolyte Fizeau |
Roue dentée : En 1849, il fabrique un ingénieux système comportant une roue dentée et deux miroirs , dont un semi-réfléchissant. Sur la figure ci-contre on devine le principe : la roue est mise en rotation , une source de lumière est réfléchie par le premier miroir , franchit une échancrure de la roue , se réfléchit sur le second miroir et parvient à l’observateur après un parcours correspondant à (2d) à la vitesse (c) qui est l’inconnue. Fizeau fait son expérience entre Montmartre et le Mont Valérien à Suresnes distants de 8633 m. La roue dentée comporte 720 dents et 720 échancrures. Fizeau détermine alors la vitesse de rotation de la roue qui permet à la lumière de traverser le bord d’un « creux » et de revenir au bord du même creux. Le faisceau est donc juste occulté et ne parvient plus à l’observateur. Cette vitesse de rotation est de 12,67 tours par seconde. |
315 000 | 5,07 % |
Temps tAR de la lumière à la vitesse de la lumière CAR durant l’aller-retour Montmartre-Suresnes : t_{AR}=\frac{D}{C_{AR}}=\frac{2 \times 8633}{C_{AR}} Vitesse angulaire V de la roue crantée : V = 12,67 tours/s = 12,67 \times 2 \pi \ rad/s La roue est composée de 720 dents et 720 échancrures, dont un secteur angulaire \alpha = \frac{2\pi }{2 \times 720} Temps tα mit par la roue pour tourner d’un angle α : t_{\alpha } = \frac{\alpha }{V}=\frac{2\pi }{2 \times 720 }\times\frac{1}{12,67 \times 2\pi }=\frac{1}{2 \times 720 \times 12,67 }Ainsi : Donc : C_{AR} = 2 \times 8633 \times 2 \times 720 \times 12,67 = 315 \ 760 \ 608 \ m/s \approx 3 \times 10^{8} \ m/s |
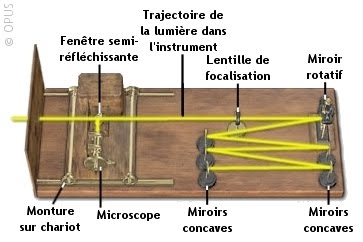
| 1862 | Léon Foucault | Miroir en rotation : C’est aussi en 1850 que Léon Foucault détermine la vitesse de la lumière, au moyen d’un miroir tournant fabriqué par Louis Breguet. Le faisceau lumineux est réfléchi par un miroir tournant à 400 tours/s, qui l’envoie sur une suite de miroirs, dont le dernier renvoie la lumière sur le trajet inverse jusqu’à une fenêtre semi-réfléchissante et un microscope qui permet de mesurer une variation d’angle de 0,0195° pour un parcours de la lumière de 40,4 m. | 298 000 | -0,60 % |
Vitesse du miroir tournant : 400 tours/s = 400 x 360° = 144 000° par seconde Donc pour un angle de 0,0195° : \frac{0,0195 \times 1}{144 \ 000}=1,354 \times 10^{-7} \ secondeVitesse de la lumière : C = \frac{D}{T} = \frac{40,4}{1,354 \times 10^{-7}}= 298\ 375 \ 184 \ m/s |
| 1878 | Albert A. Michelson | Miroir en rotation : Même procédé que Léon Foucault mais sur une distance 70,8 km et un temps de 327 x 10-6 secondes. | 299 796 | 0% | |
| 1907 | Bennett Rosa et Noah Dorsey | Constantes électromagnétiques | 299 710 | -0,03 % | |
| 1950 | Louis Essen et Albert Gordon-Smith | Cavité résonnante | 299 792,5 | 0% | |
| 1958 | K. D. Froome | Interférométrie radio | 299 792,50 | 0% | |
| 1972 | Evenson et al. | Interférométrie laser | 299 792,456 2 | 0% | |
| 1978 | Woods, Shotton et Rowley | Interférométrie laser | 299 792,458 8 | 0% | |
| 1983 | Conférence générale des poids et mesures (définition du mètre) |
Avant 1960, le mètre était la dix-millionième partie du quart du méridien terrestre passant par Paris. Une barre de platine mesurant 1 m se trouvée au Bureau international des poids et mesures à Sévre, et servait de référence. Cependant la précision n’était pas parfaite, puisque sujette aux condition de mesure. En 1983 la définition du mètre évolue. Ce sera la distance parcourue par la lumière en 1/299 792 458 seconde. Ce n’est plus la lumière que l’on mesure à partir d’une distance, mais le mètre que l’on définie à partir de la vitesse de la lumière. |
299 792,458 | 0% |
Mètre étalon en platine.
Mètre étalon 36 rue de Vaugirard 75006 |
VII°/ Les instruments de mesure de l’antiquité :
VIII°/ L’équation d’Al-Khwarizmi : 780-850 après JC
 |
 |
| Muḥammad ibn Mūsā al-Khwārizmī (en arabe : محمد بن موسى الخوارزمي), généralement appelé Al-Khwârizmî (latinisé en Algoritmi ou Algorizmi), né dans les années 780, probablement à Khiva dans la région du Khwarezm (d’où il prend son nom), dans l’actuel Ouzbékistan, mort vers 850 à Bagdad, est un mathématicien, géographe, astrologue et astronome persan. Ses écrits, rédigés en langue arabe, puis traduits en latin à partir du XIIe siècle, ont permis l’introduction de l’algèbre en Europe. Sa vie s’est déroulée en totalité à l’époque de la dynastie abbasside. | Son nom latinisé est à l’origine du mot algorithme et le titre de l’un de ses ouvrages Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (Abrégé du calcul par la restauration et la comparaison) est à l’origine du mot algèbre (al-jabr), discipline mathématique connue depuis l’antiquité. |
Voici sans doute l’exercice fondateur de l’algèbre et de la résolution des équations : Le carré d’un nombre et 10 fois ce nombre valent 39.
Si on pose x le nombre inconnu, il faut résoudre l’équation suivante en langage moderne : x² + 10x = 39
 |
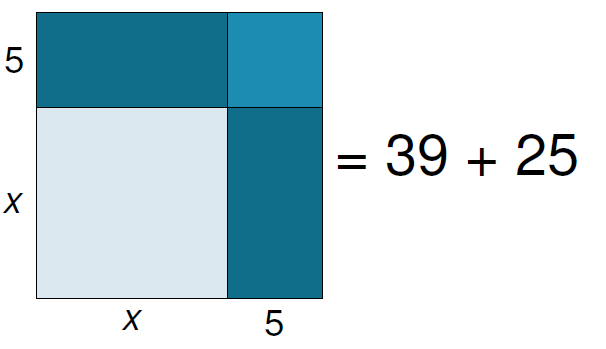 |
|
Al-Khwarizmi a utilisé une représentation géométrique pour visualiser le problème : 39 = x² + 5x + 5x = x² + 10x |
Si on rajoute un carré de 5×5 = 25 on fabrique ainsi un nouveau carré de côté x+5. On a alors : (x+5)² = 39 + 25 = 64 Il faut trouver un nombre dont le carré est égal à 64. Ce sera 8, car le nombre négatif -8 n’a pas encore beaucoup de signification à l’époque. x + 5 = 8 donc x = 8 – 5 = 3 Vérification : x² + 10x = 3² + 10×3 = 9 + 30 = 39 |