Il permet de calculer l’aire d’un triangle quand on connait seulement la longueur des 3 côtés.
En posant s = ½ Périmètre de ABC : Aire_{ABC}=\sqrt{s (s - AC)(s - BC) (s - AB)}
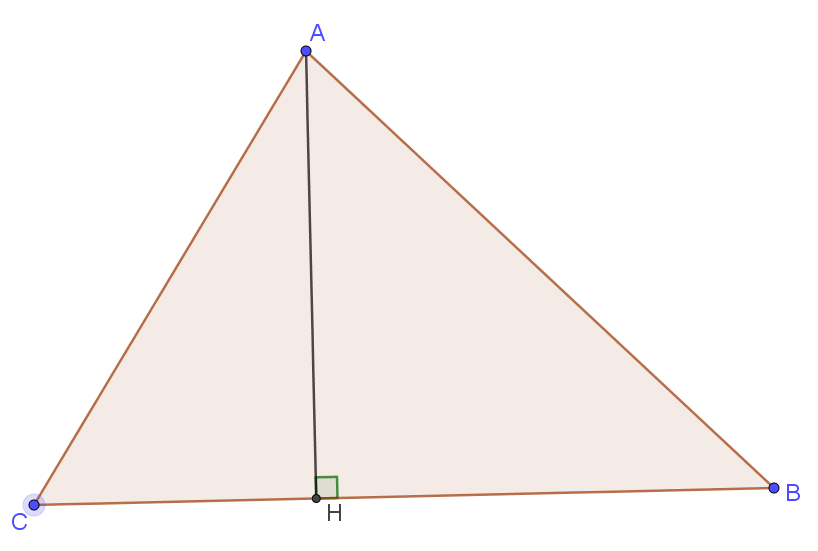
Démonstration :
| Dans le triangle ABH rectangle en H
D’après le théorème de Pythagore AB² = AH²+ HB² donc AH² = AB² – HB²
|
Dans le triangle ACH rectangle en H
D’après le théorème de Pythagore AC² = AH²+ HC² donc AH² = AC² – HC² = AC² – (BC – HB)² = AC² – BC² + 2 BCxHB – HB² |
| Donc : AB² – HB² = AC² – BC² + 2 BCxHB – HB²
AB² = AC² – BC² + 2 BCxHB HB = \frac{AB^{2}-AC^{2}+BC^{2}}{2BC}
|
Ainsi : AH² = AB² – HB² = AH² = AB² – ( \frac{AB^{2}-AC^{2}+BC^{2}}{2BC})^{2}
4AH²BC² = 4AB²BC² – (AB² – AC² + BC²)² 4AH²BC² = (2ABxBC)² – (AB² – AC² + BC²)² 4AH²BC² = (2ABxBC + AB² – AC² + BC²) (2ABxBC – AB² + AC² – BC²) 4AH²BC² = ((AB + BC)² – AC²) (AC²- (AB – BC)²) 4AH²BC² = (AB + BC + AC)( AB + BC – AC) (AC + AB – BC) (AC – AB + BC) Posons : s = ½ périmètre de ABC donc : 2s = périmètre de ABC = AB + BC + AC 2s – 2AC = AB + BC + AC – 2AC = AB + BC – AC 2s – 2BC = AB + BC + AC – 2BC = AB – BC + AC 2s – 2AB = AB + BC + AC – 2AB = -AB + BC + AC 4AH²BC² = 2s (2s – 2AC) (2s – 2BC) (2s – 2AB) 4AH²BC² = 16s (s – AC) (s – BC) (s – AB) \frac{AH^{2}BC^{2}}{4} = s (s – AC) (s – BC) (s – AB) (\frac{AH\times BC}{2})^{2} = s (s – AC) (s – BC) (s – AB) (Aire_{ABC})^{2} = s (s – AC) (s – BC) (s – AB) Aire_{ABC}=\sqrt{s (s - AC)(s - BC) (s - AB)} |