Ce n’est pas Blaise Pascal (1623 – 1662) qui l’a trouvé mais il fut nommé ainsi en son l’honneur. Il est connu sous l’appellation « triangle de Pascal » en Occident, bien qu’il fût étudié par d’autres mathématiciens, parfois plusieurs siècles avant lui, en Inde, en Perse, au Maghreb, en Chine (où il est appelé « triangle de Yang Hui »), en Allemagne et en Italie.
I°/ Construction :
II°/ Coefficients des égalités remarques : coefficients binomiaux
III°/ La combinatoire : C’est l’art de compter les objets, actions ou autre.
IV°/ Trouver les puissances de 2 :
V°/ Trouver les puissances de 11 :
VI°/ La suite Fibonacci :
VII°/ La règle de la crosse de hockey :
VIII°/ Le triangle de Sierpinski :
IX°/ Les nombres premiers :
Sa construction est simple, mais ses applications sont multiples.
I°/ Construction :
On part du nombre 1 et à chaque ligne on rajoute un nombre qui est la somme des 2 nombres qui sont au-dessus de lui. Chaque case est donc la somme des 2 cases qui sont au-dessus, s’il n’y a pas de case on prend le nombre 0. Donc dans chaque ligne, le premier et le dernier nombre est 1.
| 1 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 2 = 1 + 1 | 1 | 2 | 1 | ||||||||||||||||||||||||||||||||||||||||||||
| 4 | 1 | 3 | 3 | 1 | ||||||||||||||||||||||||||||||||||||||||||||
| 5 | 4 = 1 + 3 | 1 | 4 | 6 | 4 | 1 | ||||||||||||||||||||||||||||||||||||||||||
| 6 | 1 | 5 | 10 | 10 | 5 | 1 | ||||||||||||||||||||||||||||||||||||||||||
| 7 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||||||||||||||||||||||||||||||||||||||
| 8 | 35 = 15 + 20 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||||||||||||||||||||||||||||||
| 9 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||||||||||||||||||||||||||||||||||||||
| 10 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | ||||||||||||||||||||||||||||||||||||||
| 11 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | |||||||||||||||||||||||||||||||||||||
| 12 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | ||||||||||||||||||||||||||||||||||||
| 13 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 | |||||||||||||||||||||||||||||||||||
| 14 | 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 | ||||||||||||||||||||||||||||||||||
| 15 | 3003 = 1287 + 1716 | 1 | 14 | 91 | 364 | 1001 | 2002 | 3003 | 3432 | 3003 | 2002 | 1001 | 364 | 91 | 14 | 1 | ||||||||||||||||||||||||||||||||
| 16 | 1 | 15 | 105 | 455 | 1365 | 3003 | 5005 | 6435 | 6435 | 5005 | 3003 | 1365 | 455 | 105 | 15 | 1 | ||||||||||||||||||||||||||||||||
| 17 | 1 | 16 | 120 | 560 | 1820 | 4368 | 8008 | 11440 | 12870 | 11440 | 8008 | 4368 | 1820 | 560 | 120 | 16 | 1 | |||||||||||||||||||||||||||||||
| 18 | 1 | 17 | 136 | 680 | 2380 | 6188 | 12376 | 19448 | 24310 | 24310 | 19448 | 12376 | 6188 | 2380 | 680 | 136 | 17 | 1 | ||||||||||||||||||||||||||||||
| 19 | 1 | 18 | 153 | 816 | 3060 | 8568 | 18564 | 31824 | 43758 | 48620 | 43758 | 31824 | 18564 | 8568 | 3060 | 816 | 153 | 18 | 1 | |||||||||||||||||||||||||||||
| 20 | 1 | 19 | 171 | 969 | 3876 | 11628 | 27132 | 50388 | 75582 | 92378 | 92378 | 75582 | 50388 | 27132 | 11628 | 3876 | 969 | 171 | 19 | 1 | ||||||||||||||||||||||||||||
| 21 | 1 | 20 | 190 | 1140 | 4845 | 15504 | 38760 | 77520 | 125970 | 167960 | 184756 | 167960 | 125970 | 77520 | 38760 | 15504 | 4845 | 1140 | 190 | 20 | 1 | |||||||||||||||||||||||||||
| 22 | 1 | 21 | 210 | 1330 | 5985 | 20349 | 54264 | 116280 | 203490 | 293930 | 352716 | 352716 | 293930 | 203490 | 116280 | 54264 | 20349 | 5985 | 1330 | 210 | 21 | 1 | ||||||||||||||||||||||||||
| 23 | 1 | 22 | 231 | 1540 | 7315 | 26334 | 74613 | 170544 | 319770 | 497420 | 646646 | 705432 | 646646 | 497420 | 319770 | 170544 | 74613 | 26334 | 7315 | 1540 | 231 | 22 | 1 | |||||||||||||||||||||||||
| 24 | 1 | 23 | 253 | 1771 | 8855 | 33649 | 100947 | 245157 | 490314 | 817190 | 1144066 | 1352078 | 1352078 | 1144066 | 817190 | 490314 | 245157 | 100947 | 33649 | 8855 | 1771 | 253 | 23 | 1 | ||||||||||||||||||||||||
Chaque case est la somme des 2 cases qui sont au-dessus. C’est-à-dire que le kième terme de la nième ligne est égal au (k-1)ième terme de la (n-1)ième ligne plus le kième terme de la (n-1)ième ligne
Voilà comment on l’écrit plus simplement.
C_{n}^{k}=C_{n-1}^{k-1}+C_{n-1}^{k} ou avec l’écriture Française \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k}
remarque :
C_{n}^{k}=\frac{n!}{k!(n - k)!}
n! = 1 x 2 x 3 x 4 x…x (n – 1) x n
(n + 1)! = (n + 1) x n!
(n - 1)! = \frac{n!}{n}
Démonstration :
(n-1)!= \frac{n!}{n} \frac{n!}{k!\times (n-k)!}=\frac{(n-1)!}{(k-1)!\times(n-1-k+1)!}+\frac{(n-1)!}{k!\times(n-1-k)!} \frac{n!}{k!\times (n-k)!}=\frac{\frac{n!}{n}}{\frac{k!}{k}\times(n-k)!}+\frac{\frac{n!}{n}}{k!\times \frac{(n-k)!}{(n-k)}} \frac{n!}{k!\times (n-k)!}=\frac{\frac{n!}{n}\times k}{k!\times(n-k)!}+\frac{\frac{n!}{n}\times (n-k)}{k!\times (n-k)!} \frac{n!}{k!\times(n-k)!}=\frac{n!(\frac{k}{n}+\frac{n-k}{n})}{k!\times (n-k)!} \frac{n!}{k!\times (n-k)!}=\frac{n!(\frac{k+n-k}{n})}{k!\times (n-k)!} \frac{n!}{k!\times (n-k)!}=\frac{n!}{k!\times (n-k)!}donc : C_{n}^{k}=C_{n-1}^{k-1}+C_{n-1}^{k}
On peut aussi dire que, la somme des 2 cases est égale à celle qui est en dessous de celle de droite. C’est-à-dire que le kième terme de la nième ligne plus le (k+1)ième terme de la nième ligne et égal au le (k+1)ième terme de la (n+1)ième ligne
C_{n}^{k}+ C_{n}^{k+1}= C_{n+1}^{k+1} ou avec l’écriture Française \binom{n}{k}+\binom{n}{k+1}=\binom{n+1}{k+1}
\frac{n!}{k!\times (n-k)!}+\frac{n!}{(k+1)!\times (n-k-1)!}=\frac{(n+1)!}{(k+1)!\times (n+1-k-1)!} \frac{n!}{k!\times (n-k)!}+\frac{n!}{(k+1)\times k! \times \frac{(n-k)!}{(n-k)}}=\frac{(n+1)!}{(k+1)!\times (n-k)!} \frac{n!}{k!\times (n-k)!}+\frac{n!\times (n-k)}{(k+1) \times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1) \times k! \times (n-k)!} \frac{n!(k+1)+n!(n-k)}{(k+1)\times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1)\times k!\times (n-k)!} \frac{n!(k+1+n-k)}{(k+1)\times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1)\times k!\times (n-k)!} \frac{n!(1+n)}{(k+1)k!(n-k)!}=\frac{(n+1)n!}{(k+1)k!(n-k)!}.
II°/ Coefficients des égalités remarques : les coefficients binomiaux.
Il s’agit de développer l’expression (a+b) à l’exposant n, ou n est un entier naturel.
Par exemple : (a+b)² = a² + 2ab + b²
Et bien le triangle de Pascal permet de déterminer les coefficients de chaque membre de l’égalité. Pour cela il faut prendre les coefficients de la ligne (n-1) et élever a et b aux puissances successives.
| (a + b)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k} \ b^{k}
Formule du binôme de Newton |
\binom{n}{k} = C_{n}^{k}=\frac{n!}{k! (n - k)!)}
Coefficients de la (n-1)ième ligne du triangle de Pascal. |
| 1 | (a + b) 0 = 1 |
| 1 1 | (a + b) 1 = 1a + 1b |
| 1 2 1 | (a + b) 2 = 1a² +2ab + 1b² |
| 1 3 3 1 | (a + b) 3 = 1a3 + 3a²b + 3ab² + 1b3 |
| 1 4 6 4 1 | (a + b) 4 = 1a4 + 4a3b + 6a²b² + 4ab3 + 1b4 |
| 1 5 10 10 5 1 | (a + b) 5 = 1a5 + 5a4b + 10a3b² + 10a²b3 + 5ab4 + 1b5 |
| 1 6 15 20 15 6 1 | (a + b) 6 = 1a6 + 6a5b + 15a4b² + 20a3b3 + 15a²b4 + 6ab5 + 1b6 |
III°/ La combinatoire : C’est l’art de compter les objets, actions ou autre.
Par exemple, combien y-a-t ’il de façon de choisir k objets parmi n. Et bien ce nombre sera égal au (k+1)ième coefficient de la (n-1)ième ligne du triangle de Pascal
|
Combien y-a-t ‘il de façon de choisir 2 objets parmi 4 objets a, b, c et d : le (2 + 1) = 3ième nombre de la (4 + 1) = 5ième ligne, c’est-à-dire 6.
Voici les 6 couples que l’on peut faire : a-b ; a-c ; a-d ; b-c ; b-d ; c-d |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Combien y-a-t ‘il de façon de choisir 3 objets parmi 6 objets : le (3 + 1) = 4ième nombre de la (6 + 1) = 7ième ligne, c’est-à-dire 20.
C_{3}^{6} = \frac{6!}{3!(6 - 3)!)}= \frac{6 \times 5\times4\times3\times2}{3\times2\times3\times2}= 5 \times4 =20 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bien entendu il existe une formule qui permet de trouver ce résultat sans avoir à fabriquer le triangle de Pascal :
Le nombre de choix possible pour choisir k éléments parmi n est égal à : C_{n}^{k} = \frac{n!}{k!(n - k)!)}
donc :
Choix de 2 éléments parmi 4 (le (2 + 1) = 3ième nombre de la (4 + 1) = 5ième ligne) = C_{4}^{2} = \frac{4!}{2!(4 - 2)!)}= \frac{4\times3\times2}{2\times2}= 3 \times 2= 6
Choix de 3 éléments parmi 6 (le (3 + 1) = 4ième nombre de la (6 + 1) = 7ième ligne) = C_{6}^{3} = \frac{6!}{3!(6 - 3)!)}= \frac{6 \times 5\times4\times3\times2}{3\times2\times3\times2}= 5 \times4 =20
IV°/ Trouver les puissances de 2 :
Si on additionne tous les nombres de la ligne n on obtient 2n-1.
| n | Somme | 2n-1 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1 | 2^0 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 2 | 2 | 2^1 | |||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2 | 1 | 3 | 4 | 2^2 | ||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 3 | 3 | 1 | 4 | 8 | 2^3 | |||||||||||||||||||||||||||||||||||||||||||||
| 1 | 4 | 6 | 4 | 1 | 5 | 16 | 2^4 | ||||||||||||||||||||||||||||||||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | 6 | 32 | 2^5 | |||||||||||||||||||||||||||||||||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | 7 | 64 | 2^6 | ||||||||||||||||||||||||||||||||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | 8 | 128 | 2^7 | |||||||||||||||||||||||||||||||||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | 9 | 256 | 2^8 | ||||||||||||||||||||||||||||||||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | 10 | 512 | 2^9 | |||||||||||||||||||||||||||||||||||||||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | 11 | 1024 | 2^10 | ||||||||||||||||||||||||||||||||||||||
| 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | 12 | 2048 | 2^11 | |||||||||||||||||||||||||||||||||||||
| 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 | 13 | 4096 | 2^12 | ||||||||||||||||||||||||||||||||||||
| 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 | 14 | 8192 | 2^13 | |||||||||||||||||||||||||||||||||||
| 1 | 14 | 91 | 364 | 1001 | 2002 | 3003 | 3432 | 3003 | 2002 | 1001 | 364 | 91 | 14 | 1 | 15 | 16384 | 2^14 | ||||||||||||||||||||||||||||||||||
| 1 | 15 | 105 | 455 | 1365 | 3003 | 5005 | 6435 | 6435 | 5005 | 3003 | 1365 | 455 | 105 | 15 | 1 | 16 | 32768 | 2^15 | |||||||||||||||||||||||||||||||||
| 1 | 16 | 120 | 560 | 1820 | 4368 | 8008 | 11440 | 12870 | 11440 | 8008 | 4368 | 1820 | 560 | 120 | 16 | 1 | 17 | 65536 | 2^16 | ||||||||||||||||||||||||||||||||
| 1 | 17 | 136 | 680 | 2380 | 6188 | 12376 | 19448 | 24310 | 24310 | 19448 | 12376 | 6188 | 2380 | 680 | 136 | 17 | 1 | 18 | 131072 | 2^17 | |||||||||||||||||||||||||||||||
| 1 | 18 | 153 | 816 | 3060 | 8568 | 18564 | 31824 | 43758 | 48620 | 43758 | 31824 | 18564 | 8568 | 3060 | 816 | 153 | 18 | 1 | 19 | 262144 | 2^18 | ||||||||||||||||||||||||||||||
| 1 | 19 | 171 | 969 | 3876 | 11628 | 27132 | 50388 | 75582 | 92378 | 92378 | 75582 | 50388 | 27132 | 11628 | 3876 | 969 | 171 | 19 | 1 | 20 | 524288 | 2^19 | |||||||||||||||||||||||||||||
| 1 | 20 | 190 | 1140 | 4845 | 15504 | 38760 | 77520 | 125970 | 167960 | 184756 | 167960 | 125970 | 77520 | 38760 | 15504 | 4845 | 1140 | 190 | 20 | 1 | 21 | 1048576 | 2^20 | ||||||||||||||||||||||||||||
| 1 | 21 | 210 | 1330 | 5985 | 20349 | 54264 | 116280 | 203490 | 293930 | 352716 | 352716 | 293930 | 203490 | 116280 | 54264 | 20349 | 5985 | 1330 | 210 | 21 | 1 | 22 | 2097152 | 2^21 | |||||||||||||||||||||||||||
| 1 | 22 | 231 | 1540 | 7315 | 26334 | 74613 | 170544 | 319770 | 497420 | 646646 | 705432 | 646646 | 497420 | 319770 | 170544 | 74613 | 26334 | 7315 | 1540 | 231 | 22 | 1 | 23 | 4194304 | 2^22 | ||||||||||||||||||||||||||
| 1 | 23 | 253 | 1771 | 8855 | 33649 | 100947 | 245157 | 490314 | 817190 | 1144066 | 1352078 | 1352078 | 1144066 | 817190 | 490314 | 245157 | 100947 | 33649 | 8855 | 1771 | 253 | 23 | 1 | 24 | 8388608 | 2^23 | |||||||||||||||||||||||||
Démonstration : d’après la formule du binôme de Newton
(a + b)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}\ b^{k}Si on prend a = b = 1 on a :
(1 + 1)^{n}=2^{n}= \sum_{k=0}^{n}\binom{n}{k}\times 1^{n-k} \times 1^{k}= \sum_{k=0}^{n}\binom{n}{k}Donc 2n est égal à la somme des termes d’une ligne du triangle de Pascal.
V°/ Trouver les puissances de 11 :
C’est un peu plus compliqué et fastidieux. Les nombres du triangle de Pascal représentent les coefficients des puissances de 10 successives.
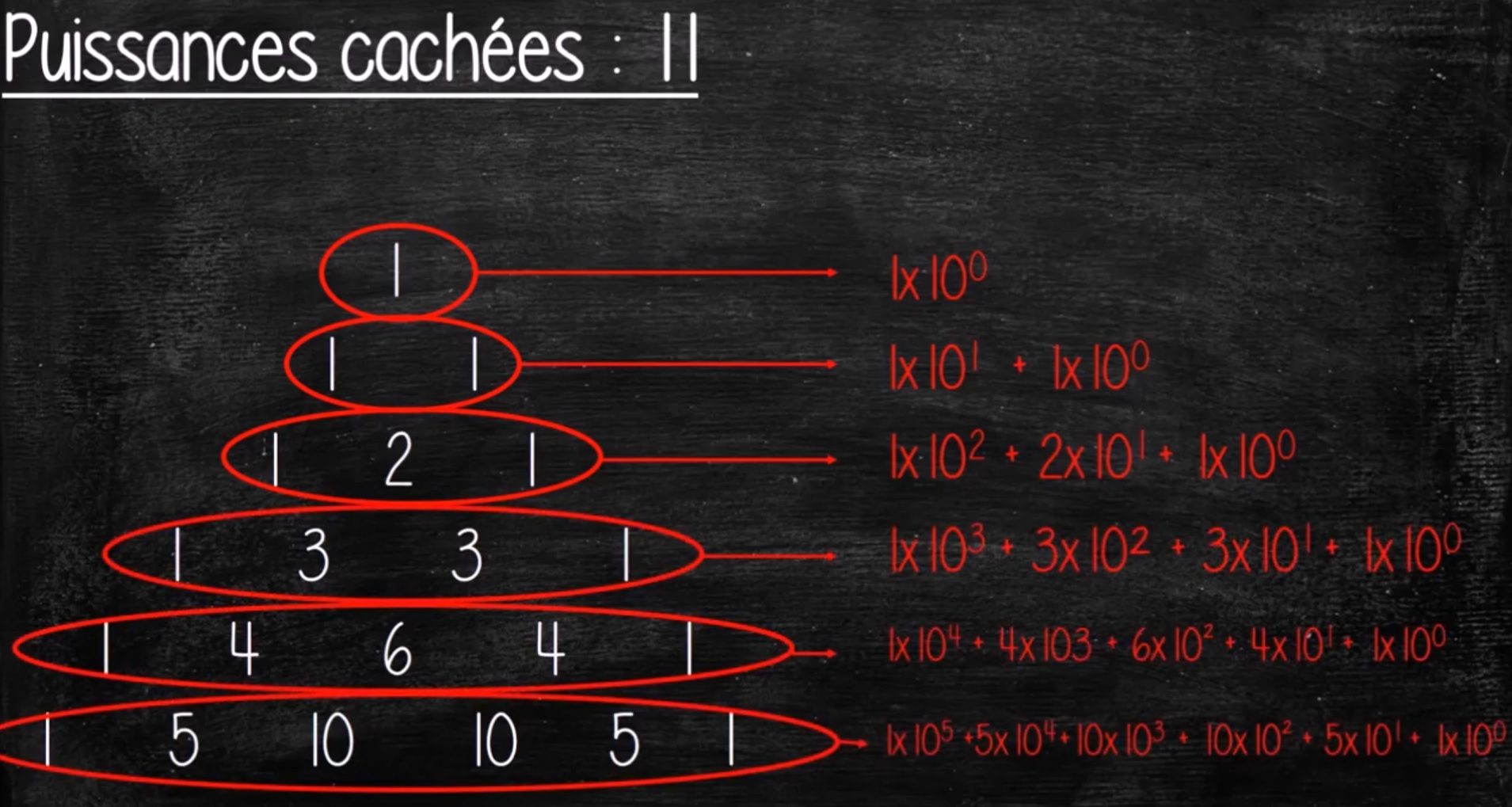 |
 |
VI°/ La suite Fibonacci :
Cette suite célèbre est constituée en partant de 0 puis 1. On obtient les nombres suivants en additionnant les deux nombres précédents.
0 ; 1 ; 1 = 0 + 1 ; 2 = 1 + 1; 3 = 2 + 1 ; 5 = 3 + 2 ….
Et bien en additionnant les diagonales ascendantes comme sur la figure ci-dessous, on obtient la suite Fibonacci.
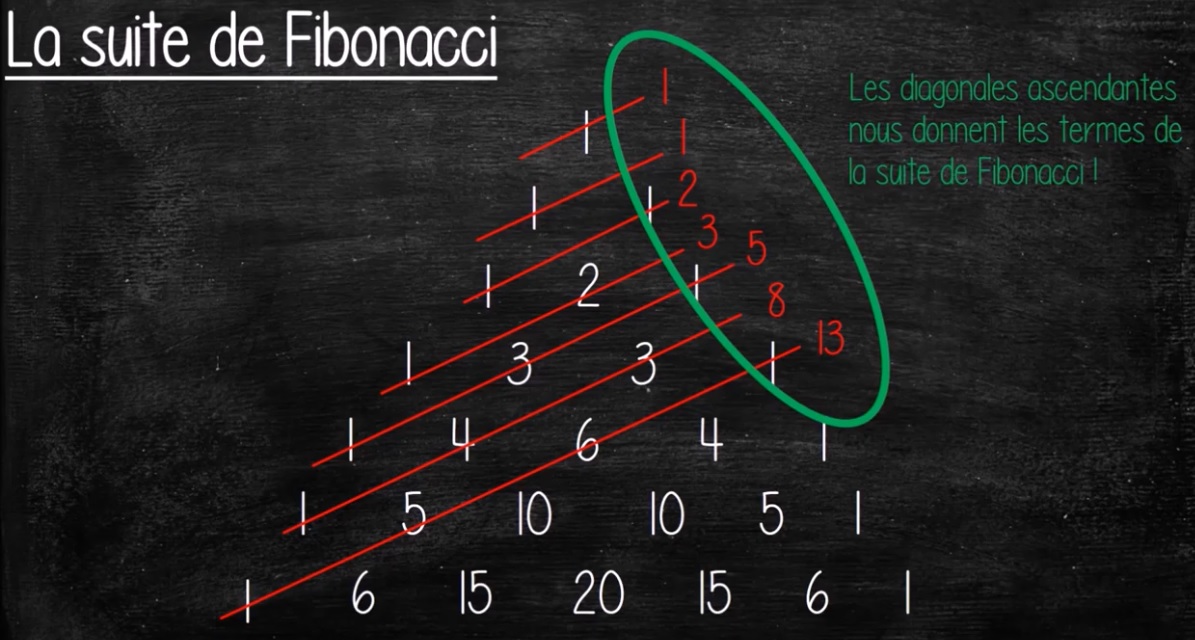
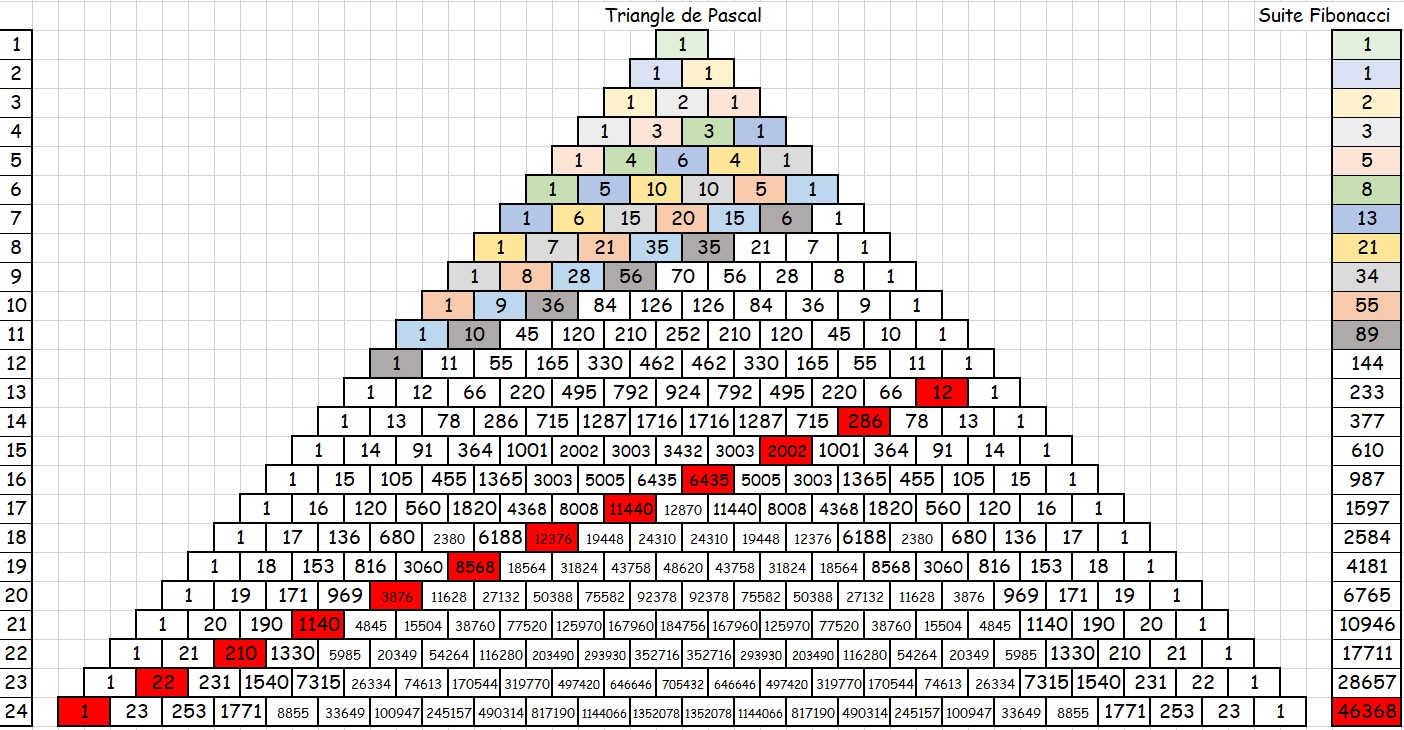
Vous aurez ici une merveilleuse horloge de Fibonacci.
|
Une autre merveille : et si on attribuait une note pour chaque chiffre et que l’on jouait la suite de Fibonacci, cela donnerait quoi ? |
John Edmark s’amuse avec Fibonacci dans des constructions de toutes beautés. Lorsqu’elle est filmée à 24 images par seconde et tournée à 550 tours par minute, chaque image représente une rotation de 137,5 degrés, ce qui équivaut à l’angle d’or. |
VII°/ La règle de la crosse de hockey :
Si on ajoute les nombres qui se suivent dans une diagonale, on obtient cette somme en bas à droite de la diagonale.
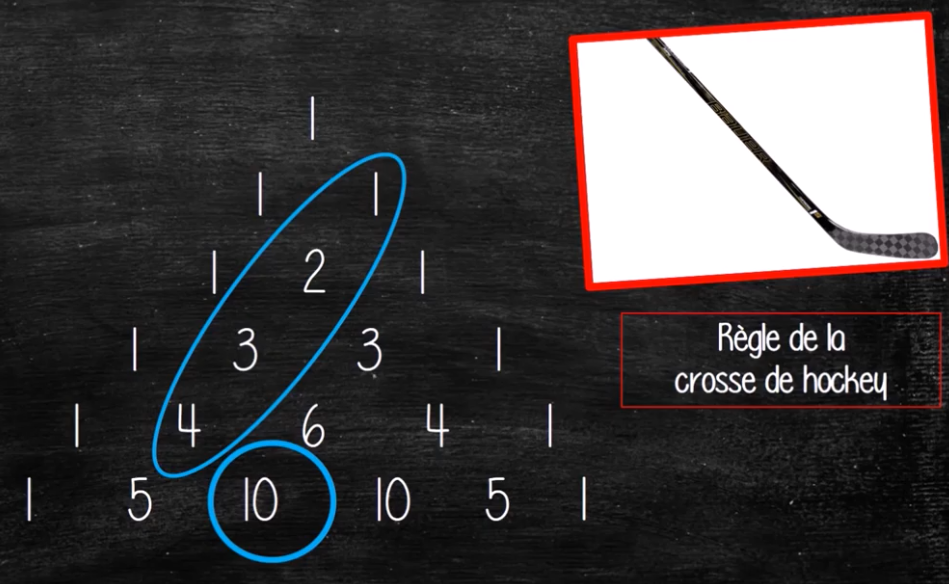
VIII°/ Le triangle de Sierpinski :
Si on enlève les nombres pairs du triangle Pascal on obtient celui de Sierpinski.

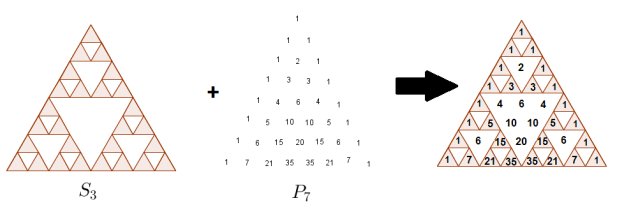 |
||
| Triangle de Sierpinski | Triangle de Pascal | Les deux |
IX°/ Les nombres premiers :
Le triangle de Pascal peut nous donner certains nombres premiers, avec une manipulation un peu fastidieuse, mais qui démontre qu’il y a une infinité de nombres premiers.
 |
 |
 |
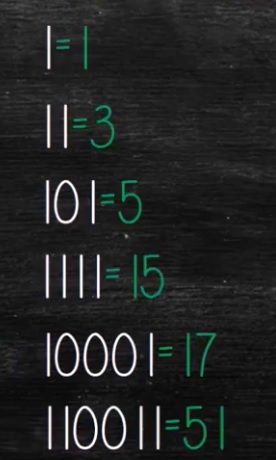 |
 |
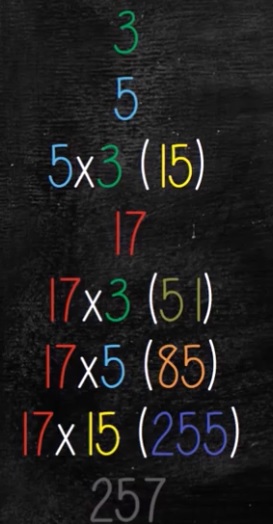 |
| Voici le début du triangle de Pascal. | Remplaçons les nombres pairs par 0 et les impairs par 1. | Rapprochons les nombres. On obtient des nombres binaires. | Traduisons les nombres binaires en nombres décimaux. | Dès que l’on a un nombre premier, il faut le multiplier successivement à tous les résultats précédents avant de retrouver un nouveau nombre premier. | |
X°/ Multiple de n de la nième ligne :
Une propriété assez étrange est que si pour la nième ligne, n est un nombre premier, alors cette ligne ne contient que des multiples de n, en enlevant les deux 1.
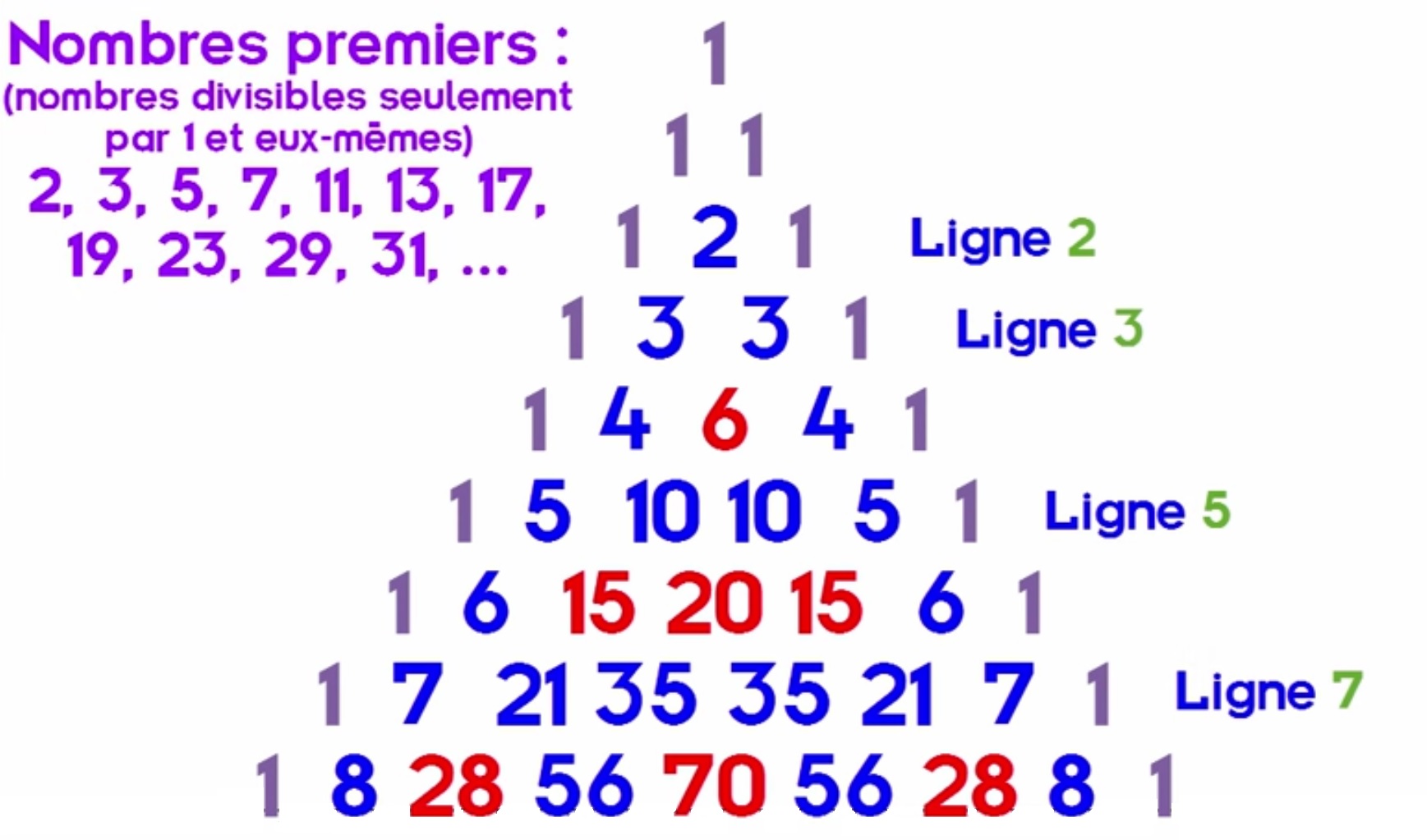
Par exemple, à la 7ième ligne, il n’y a que des multiples de 7 : 7, 21 et 35.