XVIII°/ Les graphes :

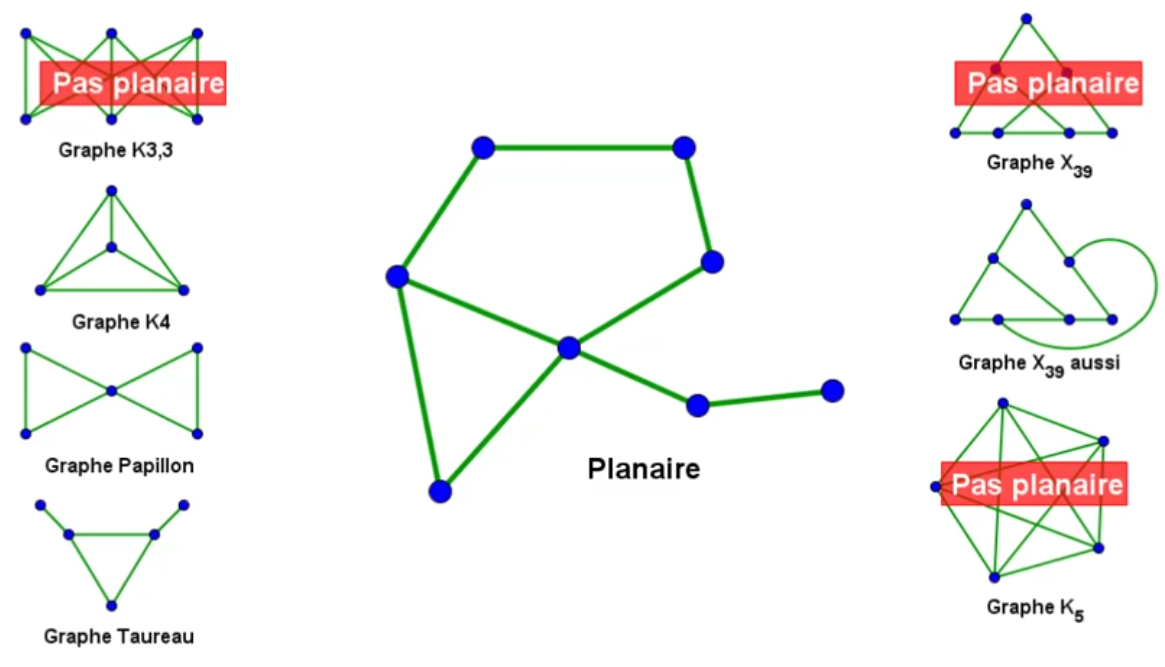
Un graphe est un ensemble points reliés par des arêtes qui peuvent être droites ou pas. Si les arêtes ne se croisent pas on dit que le graphe est planaire.

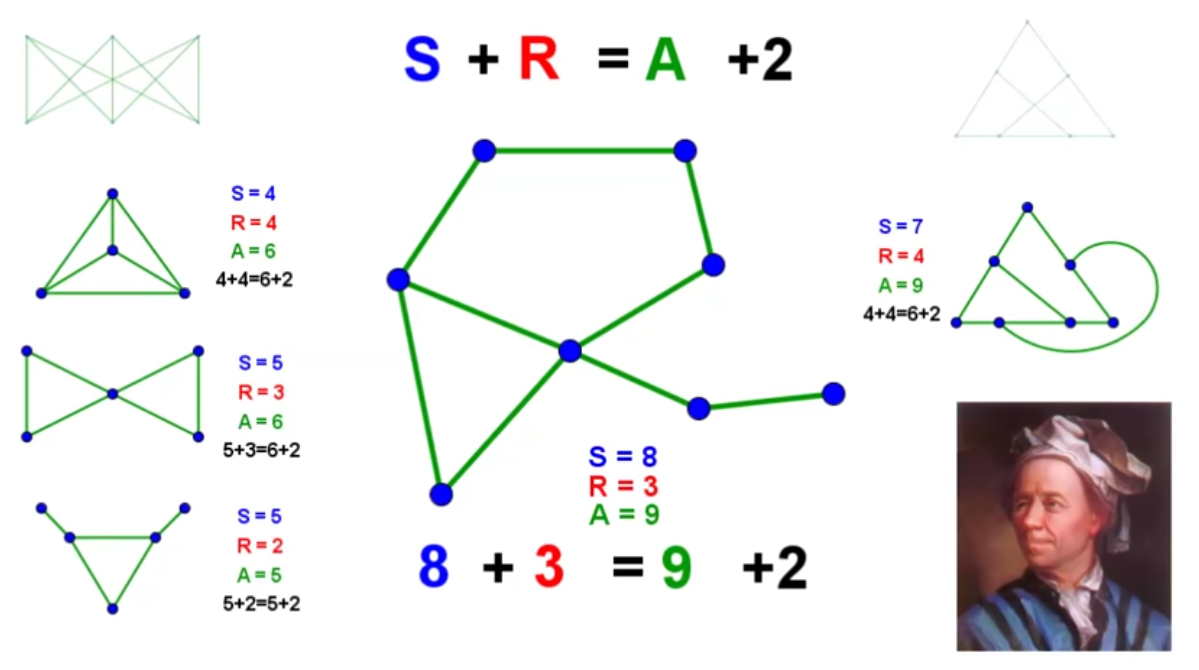
La formule d’Euler pour les graphes convexes : S + R = A + 2 (S nombre de sommets, R nombre de régions délimitées par les arêtes et A nombre d’arêtes)

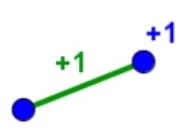
	1 points	+ 1 points = + 1 arêtes, donc pas de changement dans la formule.		+ 1 région sans sommet = + 1 arête
Schéma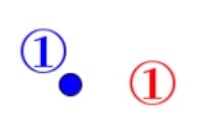
Sommet S	S = 1	S + 1 = 1 + 1 = 2	S + 4 = 5	S = 5
Régions R	R = 1	R = 1	R = 1	R = 2 + 1 = 3
Arêtes A	A = 0	A + 1 = 0 + 1 = 1	A + 4	A = 5 + 1 = 6
Formule d’Euler S + R = A + 2	1 + 1 = 0 + 2 = 2	2 + 1 = 1 + 2 = 3 S + 1 + R = A + 1 + 2 S + R = A + 2	5 + 1 = 4 + 2 = 6 S + 4 + R = A + 4 + 2 S + R = A + 2	5 + 3 = 6 + 2 = 8 S + R + 1 = A + 1 + 2 S + R = A + 2

Tour de magie :

Cette formule permet de créer un petit tour de magie assez bluffant : gribouiller n’importe comment. La seule chose qui importe, c’est que le gribouillage soit en un seul morceau (connexe). Par exemple, vous pouvez faire un truc comme ça :

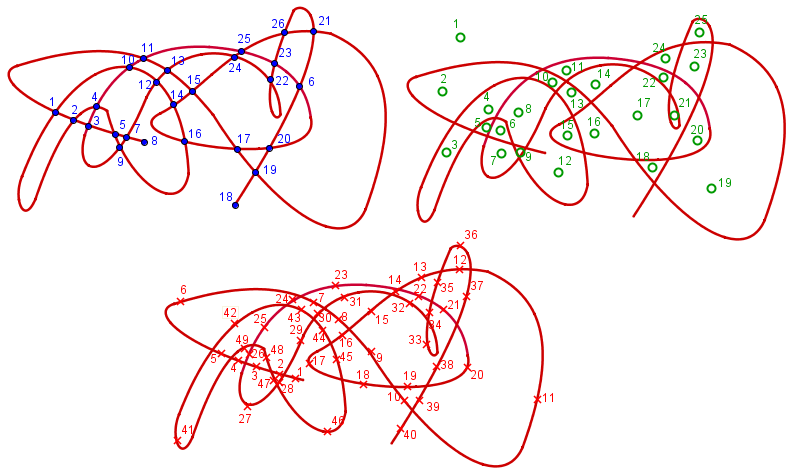C’est maintenant qu’on va faire des maths ! Dans ce gribouillage, on peut repérer des « Sommets » S (les points d’intersection et les extrémités), des « Arrêtes » A (ce qui relie deux sommets) et des « Régions » R (les cellules, délimitées par des arrêtes. Au passage, l’extérieur de la figure est une face. On les appellent souvent Face F.). Comptez-les !

Moi, je compte S = 26 sommets (bleus), A = 49 arrêtes (rouges) et F = 25 faces (verts)

Attention, tour de magie qui n’impressionnera personne. Je suis sûr que si vous effectuez l’opération S – A + F = 26 – 49 + 25 = 2, vous trouverez toujours 2 !

La formule d’Euler pour les polyèdres convexes : S + F = A + 2 (S nombre de sommets, F nombre de faces et A nombre d’arêtes).

Une très belle vidéo :