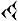A°/ Multiplication de carrés :
B°/ Nombres automorphes et miroirs :
C°/ Des carrés bizarres :
D°/ Trouver de tête des carrés et des racines carrées :
E°/ Trouver de tête des cubes et des racines cubiques :
F°/ Trouver une racine cinquième :
G°/ Bonjour les racines carrées :
H°/ Les nombres p-adiques :
I°/ \sqrt{2} est irrationnel :
J°/ Racines continues : Racines (ou radicaux) emboîtées ou imbriqués
K°/ Le carré et le cube de 69 :
L°/ Cercle « carré » parfait :
A° / Multiplication de carrés :
1 × 2 × 3 × 4 = 24 = (5² – 1)
de même: 2 × 3 × 4 × 5 = 120 = (11² – 1)
Est-il toujours vrai qu’en multipliant 4 nombres successifs on obtienne un carré moins 1 ?
Solution de l’énigme:
La réponse est OUI !!
(y – 1 ) × y × (y + 1) × (y + 2) + 1 = (y² + y – 1)²
Démonstration : (y – 1) × y × (y + 1) × (y + 2) = (y2 + y)(y2 + y – 2)
. = [(y2 + y – 1) + 1][(y2 + y – 1) – 1]
. = (y2 + y – 1)2 – 1
B°/ Nombres automorphes et miroirs :
Nombres automorphes : nombre qui apparaît à la fin de son carré.
exemple:
5² = 25
6² = 36
25² = 625
76² = 5776
Il n’existe que 2 nombres automorphes à 3 chiffres.
Quels sont-ils ?
Solution de l’énigme : 376² = 141376 et 625²=390625
Carrés miroirs : si on inverses les chiffres d’un carré ou retrouve un autre carré.
10² = 100 <-> 001 = 01²
11² = 121 <-> 121 = 11²
12² = 144 <-> 441 = 21²
13² = 169 <-> 961 = 31²
C°/ Des carrés bizarres :
. 1 / Une somme bizarre :
Il existe des nombres qui ont la particularité suivante:
Le nombre additionné du même nombre écrit dans l’ordre inverse donne un carré parfait.
Exemple : 440 + 044 = 22²
Il en existe 3 autres de 3 chiffres. Quels sont-ils ?
De Même il en existe 2 de 5 chiffres. Quels sont-ils ?
Solution de l’énigme:
990 + 099 = 33²
198 + 891 = 33²
396 + 693 = 33²
65340 + 04356 = 264²
53361 + 16335 = 264²
. 2 / Une division infaisable :
Voici une fraction proposée par S. Ratchinski, professeur de sciences naturelles, qui avait renoncé à sa chaire à l’Université de Moscou en 1895, pour de venir un simple maître d’école.
Que vaut :
Cette fraction est vraiment difficile à faire de tête, mais les nombres 10, 11, 12, 13 et 14, ont une propriété intéressante :
10² + 11² + 12² = 13² + 14² = 100 + 121 + 144 = 365
ainsi :
. 3 / Cercle « carré » parfait :
 |
Les nombres 1 à 32 sont placés le long d’un cercle sans répéter aucun nombre et pourtant la somme de deux nombres adjacents dans ce cercle est un carré parfait ! |
D°/ Trouver de tête des carrés et des racines carrées :
. 1 / Trouver un carré connaissant le précédent : la méthode de Zorro
 |
Pour connaître le carré d’un nombre (n + 1), il suffit de connaître le carré du nombre n précédent. Pour cela, il suffit d’additionner le carré n² au nombre n et à son suivant ( n + 1) : ( n + 1 )² = n² + 2n + 1 = n² + n + ( n + 1)En effet :3² = 2 + 2² + (2+1) = 2 + 4 + 3 = 910² = 9 + 9² + (9+1) = 9 + 81 + 10 = 100Sur le tableau des carrés on remarque que cette addition forme le Z de Zorro !!! |
. 2 / Trouver le carré d’un nombre dont le chiffre des unités est 5 :
Pour trouver le carré d’un nombre n dont le chiffre des unités est 5, il suffit de multiplier le nombre de dizaines de n par le nombre suivant et d’ajouter 25.
Exemple :
| n | 45 | 85 | 205 |
| Produit | 4 x 5 = 20 | 8 x 9 = 72 | 20 x 21 = 420 |
| n² | 2 025 | 7 225 | 42 025 |
Si on a : n = 10d + 5 alors : (10d + 5)² = (10d)² + 2x10dx5 + 5² = 100d² + 100d + 25 = 100d(d+1) + 25
Le résultat a pour nombre de centaines le produit d(d+1) c‘est à dire le nombre de dizaines de n par le nombre suivant, et on écrit 25 à droite du produit d(d+1).
. 3 / Trouver un carré par la méthode du rectangle :
Allez voir ici : chapitre c/
. 4 / Trouver mentalement une racine carrée :
Connaissant le carré n² d’un nombre n ( si n2< 1 000 000 ), on peut retrouver le nombre n, c’est-à-dire la racine carrée de n².
– Après avoir enlever les 2 derniers chiffres de n², chercher le carré parfait juste inférieur au nombre obtenu. La racine carrée de ce carré donne le chiffre des dizaines de n.
– Le dernier chiffre de n² ne peut correspondre qu’à deux chiffres maximums donnant le dernier chiffre de n :
| Le dernier chiffre de n² | 0 | 1 (1 ou 81 ) | 4 (4 ou 64) | 5 ( 25 ) | 6 (16 ou 36) | 9 (9 ou 49) |
| Le dernier chiffre de n | 0 | 1 ou 9 | 2 ou 8 | 5 | 4 ou 6 | 3 ou 7 |
Exemple : n² = 6 561 → 6 400 > 6 561 > 8 100 ( ou 64 > 65 > 81 )
. → 8² > 65 > 9²
9² étant trop grand, le chiffre des dizaines de n est 8.
Le dernier chiffre de n² étant 1, le dernier chiffre de n ne peut être que 1 ou 9. Or 85² = 7 225 (Allez voir ici : chapitre c/ ), donc trop grand pour n², ainsi que 89².
Ainsi n est égal à 81.
. 5 / L’extraction d’une racine carrée à la main : A la manière de nos grand parents.
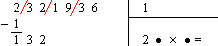
| La présentation ressemble à celle de la division : le nombre dont on recherche la racine est écrit à la place du dividende, la racine elle-même sera à la place du diviseur. | |
| 1. On partage le nombre dont on recherche la racine par paquets de 2 chiffres en partant de la droite (le dernier paquet possède donc 1 ou 2 chiffres) |
|
| 2. On cherche le plus grand carré inférieur à la première tranche (celle de gauche) et on inscrit sa racine à la place du ‘diviseur’. |
|
| 3. On retranche ce carré de la première tranche et on abaisse la tranche suivante. |
On obtient alors ici 132 |
| 4. On double la racine obtenue et on l’inscrit à la place du quotient. |
|
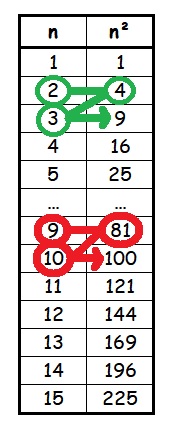
| 5. Il faut maintenant écrire à la droite de ce nombre (ici c’est 1) le plus grand chiffre x de sorte que le produit par x ne dépasse pas le nombre obtenu au dividende. |
On cherche donc un nombre pour que 2 • × • ≤ 132. On a 25 × 5 = 125 et 26 ´ 6 = 156. Le chiffre x cherché est donc 5.( x = • ) |
| 6. On inscrit x à gauche du diviseur et on soustrait le produit obtenu dans la partie dividende. |
|
| 7. On recommence ensuite en abaissant la tranche suivante et en continuant à l’étape 4. |
|
| La dernière étape (avec un chiffre après la virgule) est :
(On peut bien sûr continuer tant que le reste est non nul…) |
|
. 6 / L’extraction d’une racine carrée à la main par soustractions : La méthode du compte-goutte
Pour avoir la racine carrée d’un nombre qui est un carré parfait, on soustrait la suite des nombres impairs à partir de 1, jusqu’à l’obtention d’un résultat nul. En effet, pour passer d’un carré au suivant il suffit d’ajouter un impair :
1² = 1 = 0 + 1
2² = 4 = 1 + 3
3² = 9 = 4 + 5
4² = 16 = 9 + 7
On compte alors le nombre d’entiers enlevés. Le résultat donne la racine carrée.
16 – 1 = 15
15 – 3 = 12 Il y a 4 soustractions
12 – 5 = 7 Donc la racine carrée de 16 est 4.
7 – 7 = 0
Pour avoir la racine carrée d’un nombre quelconque, on procède de même jusqu’à ce qu’on ne puisse plus obtenir un nombre positif. On compte le nombre d’entiers enlevés et l’on a une valeur approchée à une unité près par défaut, du résultat.
106 – 1 = 105
105 – 3 = 102
102 – 5 = 97
97 – 7 = 90 Il y a 10 soustractions
90 – 9 = 81 Donc la racine carrée de 106 est 10 à 1 près par défaut.
81 – 11 = 70
70 – 13 = 57
57 – 15 = 42
Évidemment nos calculettes sont plus rapides et efficaces, mais ce procédé très ancien reste très simple.
42 – 17 = 25
25 – 19 = 6
Une variante : La méthode du compte-goutte :
| Cherchons la racine carrée de 2 137 | |
| 1. On partage le nombre dont on recherche la racine par paquets de 2 chiffres en partant de la droite (le dernier paquet possède donc 1 ou 2 chiffres) en partant de la virgule : 21 37, 00 00 | |
| 2. Du premier groupe 21, on ôte les premiers nombres impairs. Nous avons effectués quatre soustractions, le premier chiffre de la racine est donc un 4. |
21 – 1 – 3 – 5 – 7 = 5 |
| 3. On prend le dernier résultat 5 et on lui « colle » la suite 37 du nombre de départ. |
5 × 100 + 37 = 537 |
| 4. On multiplie le dernier impair 7 de la soustraction précédente par 10 et on ajoute 11. |
7 × 10 + 11 = 81 |
| 5. On soustrait à 537 les impairs à partir de 81. Nous avons effectués 6 soustractions, le deuxième chiffre de la racine est donc 6. |
537 – 81 – 83 – 85 – 87 – 89 – 91 = 21 |
| 6. On peut continuer. On multiplie le dernier impair 91 de la soustraction précédente par 10 et on ajoute 11. |
91 × 10 + 11 = 921 |
| 7. On prend le dernier résultat 21 et on lui « colle » la suite 00 du nombre de départ. On soustrait les impairs à partir de 921. Nous avons effectués 2 soustractions, la 1ière décimale de la racine est donc 2. |
2100 – 921 – 923 = 256 |
| 8. On continue. Nous avons effectués 2 soustractions, la 2ième décimale de la racine est donc 2. |
923 × 10 + 11 = 9241 25600 – 9241 – 9243 = 7116 |
Voici un fichier Excel pour vérifier : Racine carrée compte goutte (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)
. 7 / L’extraction d’une racine carrée : Algorithme de Héron d’Alexandrie
L’algorithme de héron d’Alexandrie est un algorithme très ancien (premier siècle) qui permet de calculer avec une très grande précision (convergente quadratique) une racine carrée.
Voici un fichier Excel pour manipuler : Algorithme de Heron d’Alexandrie (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)
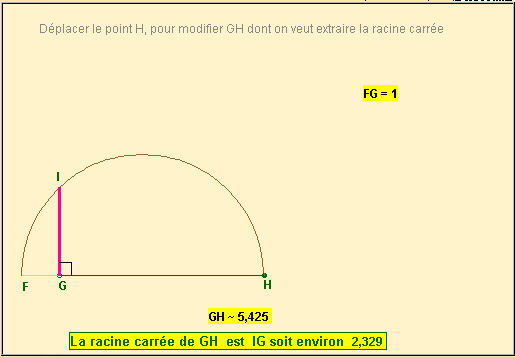
. 8/ L’extraction d’une racine carrée à la règle et au compas :
Cette méthode très simple est attribuée à Descartes. Elle nécessite seulement une règle et un compas.
Si on cherche la racine carrée d’un nombre n, il suffit :
– de tracer un demi-cercle de diamètre 1+n, donc de rayon (1+n)/2
– tracer un diamètre [FH] de ce cercle
– marquer sur le diamètre le point G tel que GF = 1
– tracer la perpendiculaire en G au diamètre [FH].
Cette perpendiculaire coupe le cercle en I. IG a pour mesure la racine carrée de n.
|
. 9/ L’escargot de Pythagore :
 |
En généralisant ce principe, un triangle avec les côtés adjacents à l’angle droit de longueur \sqrt{n} et 1 a une hypoténuse de longueur \sqrt{n+1}. |
. 10/ Les dents de requin :
 |
Dans un repère orthonormé on trace les droites y = 0 et y = 1, puis :
|
E°/ Trouver de tête des cubes et des racines cubiques :
. 1 / Trouver mentalement une racine cubique :
Connaissant le cube n3 d’un nombre n ( si n3< 1 000 000 ), on peut retrouver le nombre n, c’est-à-dire la racine cubique de n3.
– Après avoir enlevé les 3 derniers chiffres de n3, chercher le cube parfait juste inférieur au nombre obtenu. La racine cubique de ce cube donne le chiffre des dizaines de n. Il faut bien sur connaître les cubes de 0 à 9.
– Le dernier chiffre de n3 ne peut correspondre qu’à un seul chiffre inférieur à 10, donnant le dernier chiffre de n. Pour 0, 1, 4, 5, 6 et 9 le dernier chiffre de n3 est le même que pour n. Pour 2, 3, 7 et 8 il faut faire la soustraction de 10 et de ce chiffre :
| Le dernier chiffre de n3 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Le dernier chiffre de n |
0 03=0 |
1 13=1 |
8 83=512 |
7 73=343 |
4 43=64 |
5 53=125 |
6 63=216 |
3 33=27 |
2 23=8 |
9 93=729 |
|
a |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
a3 |
03=0 |
13=1 |
23=8 |
33=27 |
43=64 |
53=125 |
63=216 |
73=343 |
83=512 |
93=729 |
Exemple : n3 = 636 056 → 512 > 636 > 729
. → 83 > 636 > 93
93 étant trop grand, le chiffre des dizaines de n est 8.
Le dernier chiffre de n3 étant 6, le dernier chiffre de n ne peut être que 6.
Ainsi n est égal à 86.
. 2/ L’extraction d’une racine cubique : A la manière de nos grand pères.
Le principe ressemble à celui de l’extraction de la racine carrée.
Exemple : Extrayons la racine cubique de 97 652 328
| On découpe le nombre de 3 en 3 en partant de la droite 97 652 328. Puis on cherche le nombre dont le cube est le plus proche par défaut de 97. C’est 4 dont le cube est 64. On soustrait 64. |
 |
| On cherche alors le plus grand nombre a tel que ( 30 x 4a x 4 + a2 ) x a <= 33 652 Rem : 4a est le nombre constitué de 4 dizaines et de a unités. |
 |
| On cherche alors le plus grand nombre a tel que
( 30 x 46a x 46 + a2 ) x a <= 33 652 Rem : 46a est le nombre constitué de 46 dizaines et de a unités. |
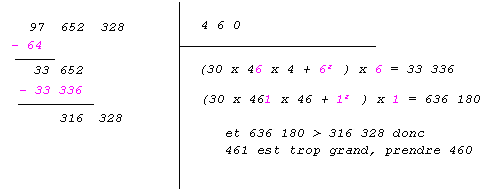 |
Finalement la racine cubique de 97 652 328 est 460 à 1 unité près par défaut.
On peut vérifier le résultat en l’élevant à la puissance 3 ou sur calculette en calculant 97 652 328 à la puissance (1/3)
. 3/ L’extraction d’une racine cubique avec 2 équerres :
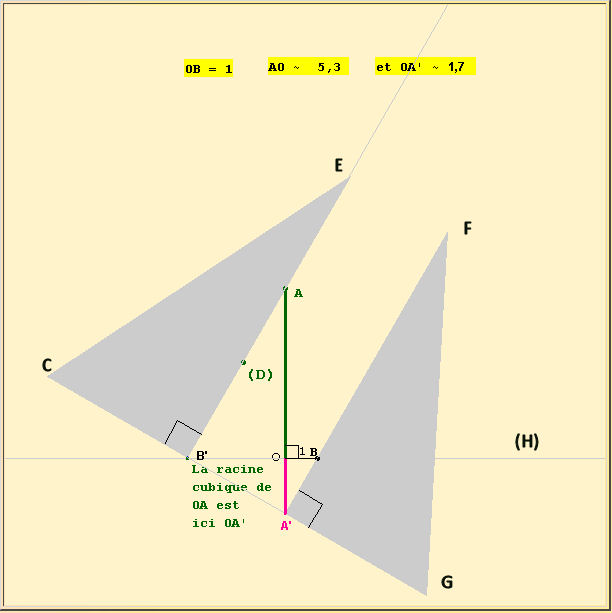 |
Le principe repose sur les propriétés de la hauteur du triangle rectangle.
Dans le triangle rectangle AB’A’ : OB’² = OA × OA’ (1) Dans le triangle rectangle BA’B’ : OA’² = OB × OB’ et comme OB=1, on a : OA’² = OB’ Donc : OA’ 4 = OB’² (2) En utilisant (1) et (2) on obtient : OA’ 4 = OB’² = OA × OA’ Donc : OA’ 3 = OA Et OA’ est bien la racine cubique de OA. |
Pour construire un tel appareil :
– AA’ doit être gradué.
– Points fixes : OB = 1cm et les équerres
– Points mobiles : A et A’- Points reliés et alignés mais articulés : C, B’, A’ et G.
– Une baguette fixe (H) sur (OB)
Si OB = 1cm est trop petit, prendre : OB = 8cm et les graduations sur OA 4 fois plus petites que sur OA’.
OA’² = OB × OB’ = 8OB → OA’ 4 = 64OB’² = 64 OA × OA’
. → OA’ 3 = 64OA = 43OA
. ![]()
. 4/ L’extraction d’une racine cubique par une abaque :
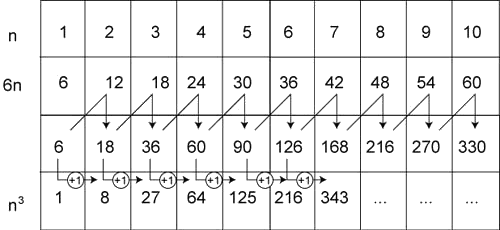
L’abaque suivant permet de calculer facilement les cubes des nombres entiers par des additions. Les flèches sont des additions.
F°/ Trouver une racine cinquième :
Connaissant la puissance cinquième n5 d’un nombre n de deux chiffres, il est possible de retrouver la racine cinquième de ce nombre n5 sans machines à calculer.
– La puissance cinquième n5 et n ont exactement le même chiffre des unités.
– Pour trouver le chiffre des dizaines de n, il suffit de connaître par cœur le tableau ci-dessous : supprimer les cinq derniers chiffres de la puissance cinquième n5, et regarder où se place le nombre alors obtenu dans le tableau (on peut apprendre par cœur l’ordre de grandeur). La borne inférieure de a donne alors le chiffre des dizaines de n.
|
a |
a5 |
Ordre de grandeur de a5 |
|
|
1 |
1 | 1 | Exemple : n5 = 6 436 343 → 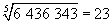
32 > 64 > 243 → 32 nous donne 2 comme chiffre des dizaines |
|
2 |
32 | 30 | |
|
3 |
243 | 250 | |
|
4 |
1 024 | 1 000 | |
|
5 |
3 125 | 3 000 | |
|
6 |
7 776 | 8 000 | |
|
7 |
16 806 | 17 000 | |
|
8 |
32 768 | 33 000 | |
|
9 |
59 049 | 60 000 |
G°/ Bonjour les racines carrées :
1/ La formule du bicentenaire :

2/ Quel calcul !
Combien fait ce calcul démentiel ?
\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+...+\frac{1}{\sqrt{288}+\sqrt{289}} = \\L’astuce consiste a utiliser la forme conjuguée du dénominateur :
\frac{1}{\sqrt{m}+\sqrt{n}} = \frac{\sqrt{n}-\sqrt{m}}{(\sqrt{m}+\sqrt{n})\times (\sqrt{n}-\sqrt{m})}=\frac{\sqrt{n}-\sqrt{m}}{\sqrt{n}^{2}-\sqrt{m}^{2}}=\frac{\sqrt{n}-\sqrt{m}}{n - m}= \sqrt{n}-\sqrt{m}Ainsi en simplifiant :
\frac{1}{{\color{Red} \textbf{1}}+\sqrt{\color{Blue} \textbf{2}}}+\frac{1}{\sqrt{\color{Blue} \textbf{2}}+\sqrt{\color{green} \textbf{3}}}+\frac{1}{\sqrt{\color{green} \textbf{3}}+\sqrt{4}}+...+\frac{1}{\sqrt{288}+\sqrt{289}} = \\ \\ \sqrt{\color{Blue} {\cancel 2}}-\sqrt{\color{Red} {1}}+\sqrt{\color{green} {\cancel 3}}-\sqrt{\color{Blue} {\cancel 2}}+\sqrt{\cancel 4}-\sqrt{\color{green} {\cancel 3}}+ ... +\sqrt{289}-\sqrt{2\cancel88} = \\ \\ \sqrt{289}-\sqrt{\color{Red} {1}}= 17 - 1 = {16}
H°/ Les nombres p-adiques :
Les nombres p-adiques sont des nombres qui, contrairement aux nombres usuels, possèdent une infinité de chiffres avant la virgule et éventuellement un nombre fini après.
Prenons le nombre 5 et élevons-le au carré. Puis recommençons à l’élever au carré un nombre infini de fois. Et bien nous obtenons un nombre p-adique qui a la particularité de ce terminer par les mêmes chiffres.
| 50 | 5 |
| 52 | 25 |
| 54 | 625 |
| 58 | 390625 |
| 516 | 152587890625 |
| 532 | 23283064365386962890625 |
| 564 | 542101086242752217003726400434970855712890625 |
| 52n | …890625 |
De même, si on prend 2 comme nombre de départ et qu’on l’élève à la puissance 5 de façon successive, on observe le même phénomène.
| 20 | 2 |
| 25 | 32 |
| 225 | 33554432 |
| 2125 | 42535295865117307932921825928971026432 |
| 2625 | …7963704661873320009853338386432 |
| 25n | …86432 |
Un outil pour calculer les très grandes puissances qui sont inaccessibles aux calculatrices : https://www.dcode.fr/calcul-exponentiation
I°/ \sqrt{2} est irrationnel :
|
La première évocation de la \sqrt{2} remonte aux Babyloniens (entre 1900 et 1600 avant notre ère). On en trouve la trace sur une tablette d’argile qui répond au doux nom de YBC_7289 (Yale Babylonian Collection aux USA) et qui fut trouvée en 1612 lors de fouille à Babylone en Irak. Il s’agirait d’un exercice permettant de calculer la diagonale d’un carré de côté 30 unités. |

YBC_7289 |
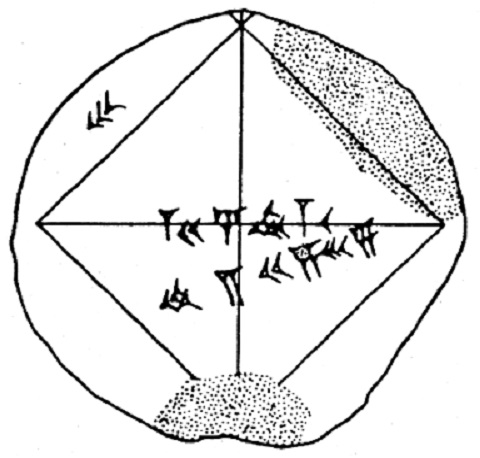 |
Rien n’indique que les scribes Babyloniens avaient une idée du caractère irrationnel de ce nombre. Cette tablette reste remarquable quand on pense qu’il faudra attendre encore plus de 12 siècles avant de voir réapparaître \sqrt{2} chez les Grecs. Pour rappel les Babyloniens compter en base 60, donc :
|
Démontrons à présent que \sqrt{2} est irrationnel.
a/ 1ière méthode :
Si \sqrt{2} était rationnel il s’écrirait sous la forme d’une fraction irréductible de 2 nombres entiers :
| \sqrt{2}=\frac{a}{b} et donc : 2=\frac{a^{2}}{b^{2}} | \Rightarrow 2b^{2} =a^{2} donc a² est pair ainsi que a qui pourrait s’écrire a = 2n. |
| \Rightarrow 2b^{2} =(2n)^{2}=4n^{2} | |
| \Rightarrow b^{2} =2n^{2} donc b² est lui aussi pair ainsi que b |
Cependant si a et b sont pairs on peut les simplifier, ce qui contredit la proposition initiale qui stipulait que \frac{a}{b} était une fraction irréductible.
b/ 2ième méthode :
Si \sqrt{2} était rationnel il s’écrirait sous la forme d’une fraction irréductible de 2 nombres entiers :
\sqrt{2}=\frac{a}{b} et comme \sqrt{2}\approx 1,41... on sait que : 1 < \sqrt{2}<2
\frac{a}{b} > 1 donc a > b et \frac{a}{b} < 2 donc a < 2b en faisant passer b de l’autre côté de l’inéquation.
Donc : b < a < 2b
Posons : c = 2b – a c’est-à-dire les écarts de a avec b et 2b
. d = a – b
\frac{c}{d}=\frac{2b-a}{a-b}=\frac{2-\frac{a}{b}}{\frac{a}{b}-1}=\frac{2- \sqrt{2}}{\sqrt{2}-1}=\frac{(2- \sqrt{2})(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}=\frac{2\sqrt{2}+2-2-\sqrt{2}}{2-1}= \sqrt{2}On peut aussi faire autrement :
Calculons : c² – 2d² = (2b – a)² – 2(a – b)² = 4b² – 4ab + a² – 2a² + 4ab – 2b² = -a² + 2b² = b^{2}(\frac{-a^{2}}{b^{2}}+2)=b^{2}(- \sqrt{2}^{2}+2)=b^{2}\times 0=0
Donc : c² – 2d² = 0 donc : \frac{c^{2}}{d^{2}}=2 et alors : \frac{c}{d}=\sqrt{2}
Comparons b et d : on sait que a < 2b donc a – b < 2b – b et enfin :
d < b
Donc : \sqrt{2} = \frac{a}{b}=\frac{c}{d}=\frac{e}{f}=...
avec : b > d > f
On vient d’écrire \sqrt{2} comme une suite de fraction dont le
dénominateur est de plus en plus petit, ce qui est impossible
J°/ Racines itératives de Ramanujan : Racines emboîtées ou imbriqués
Il existe des racines continues, suite de radicaux emboîtés, qui finissent par donner des valeurs très particulières.
Par exemple avec la \sqrt{2} :
{\color{Red} \sqrt{2 + 2}} = \sqrt{4}=2 \\ \sqrt{2 + {\color{Red} \sqrt{2 + 2}}} = \sqrt{4}=2 \\ \sqrt{2 + \sqrt{2 + {\color{Red} \sqrt{2 + 2}}}} = \sqrt{4}=2 \\ \sqrt{2 + \sqrt{2 + \sqrt{2 + {\color{Red} \sqrt{2 + ...}}}}} = \sqrt{4}=2 \\Ainsi on obtient toujours le nombre 2, quelque soit la longueur du calcul.
On peut généraliser cet exploit avec n’importe quel nombre entier n, en utilisant la formule suivante : posons r = n( n – 1)
n = {\color{Red} \sqrt{r + n}} \\ n = \sqrt{r + {\color{Red} \sqrt{r + n}}} \\ n = \sqrt{r + \sqrt{r + {\color{Red} \sqrt{r + ...}}}}Ainsi :
| n | r = n( n – 1) | n = \sqrt{r + \sqrt{r + {\color{Red} \sqrt{r + ...}}}} |
| 3 | 3 x 2 = 6 | 3 = \sqrt{6 + \sqrt{6 + {\color{Red} \sqrt{6 + 3}}}} |
| 4 | 4 x 3 = 12 | 4 = \sqrt{12 + \sqrt{12 + {\color{Red} \sqrt{12 + 4}}}} |
| 5 | 5 x 4 = 20 | 5 = \sqrt{20 + \sqrt{20 + {\color{Red} \sqrt{20 + 5}}}} |
| 6 | 6 x 5 = 30 | 6 = \sqrt{30 + \sqrt{30 + {\color{Red} \sqrt{30 + 6}}}} |
Mais on peut trouver des racines imbriquées encore plus terrifiantes qui donnent pourtant des résultats tout à fait simples :
\sqrt{1+1\sqrt{1+1\sqrt{1+1\sqrt{1+1\sqrt{1+...}}}}} = \frac{1+\sqrt{5}}{2} = \varphi = Le \ nombre\ d'or \\ \sqrt{2+1\sqrt{2+1\sqrt{2+1\sqrt{2+1\sqrt{2+...}}}}} = 2 \\ \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+5\sqrt{1+...}}}}} = 3 \\ \sqrt{6+2\sqrt{7+3\sqrt{8+4\sqrt{9+5\sqrt{10+...}}}}} = 4Ce sont des formules découvertes par le génial Mathématicien Indien Ramanujan :
n\sqrt{1 + (n+1)\sqrt{1+(n+2)\sqrt{1+(n+3)\sqrt{1+(n+4)\sqrt{1+...}}}}} = n( n+ 2))\\ n\sqrt{(n+5) + (n+1)\sqrt{(n+6)+(n+2)\sqrt{(n+7)+(n+3)\sqrt{(n+8)+(n+4)\sqrt{(n+9)+...}}}}} = n( n+ 3))Il suffit de remplacer n par 1 et on retrouve les deux dernières formules précédentes.
Quelques remarquables racines carrées imbriquées infinies de 2remarquables carrés imbriqués de 2 :
K°/ Le carré et le cube de 69 :
69 est le seul nombre naturel dont le carré 69² = 4 761 et le cube 693 = 328 509 utilisent chaque chiffre décimal de 0 à 9 exactement une fois.
L°/ Cercle « carré » parfait :
Les nombres 1 à 32 sont placés le long de la circonférence d’un cercle sans répéter aucun nombre et pourtant la somme de deux nombres adjacents dans ce cercle est un carré parfait !

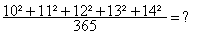
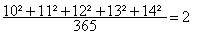
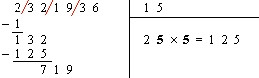
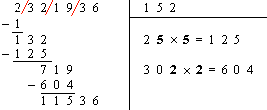
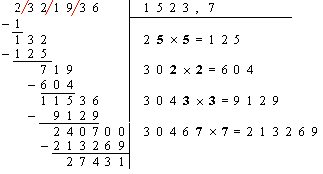
 c’est à dire 30.
c’est à dire 30.


 c’est à dire
c’est à dire