Pour effectuer de très grosses multiplications vous utilisez une machine à calculer, mais elle va très vite être limitée. Voici une calculatrice qui ne vous laissera pas en plan !!
En ligne, voici une autre calculatrice : https://www.dcode.fr/multiplication-grands-nombres
A°/ Les très grosses multiplications : La multiplication Grecque ou Italienne :
B°/ Les très grosses divisions :
C°/ La méthode mentale du rectangle : calcul mental
D°/ Trouver le dernier chiffre d’un quotient :
E°/ Méthode manuelle pour effectuer les multiplications :
F°/ Différentes méthodes de multiplication :
1°/ Multiplication babylonienne (Somme de carrés en Mésopotamie)
2°/ Multiplication égyptienne :
3°/ Multiplication Russe :
4°/ La multiplication per Gelosia Grecque ou Italienne :
5°/ Méthode des lignes : multiplication Japonaise
6°/ Méthode des cercles :
7°/ Méthode des bâtons de Neper dit aussi de Napier :
G°/ Multiplication de 2 nombres proches de 100 :
H°/ Tables de multiplication façon modulo :
I°/ Des simplifications bizarres :
J°/ Décomposition en facteur premiers :
K°/ La notation Polonaise :
A°/ Les très grosses multiplications : La multiplication Grecque ou Italienne
A l’aide d’une machine à calculer, si l’on effectue la multiplication de 987 654 × 745 321, la machine à calculer nous donnera le résultat suivant : 7,361 192 669 × 1011, c’est-à-dire approximativement 736 119 000 000. En effet son écran est limité à certain nombre de caractères, en général 17 chiffres, et elle préfère donner la réponse sous forme scientifique.
Comment trouver les six derniers chiffres exactement ?
Bien sûr, si on utilise la calculatrice de Windows, on obtiendra la valeur exacte car elle n’est ps limiter par le nombre de caractères : 987 654 × 745 321 = 736 119 266 934
Pour comprendre comment utiliser une calculatrice, qui ne sait multiplier que des nombres de trois chiffres (par exemple), pour faire des multiplications de nombres composés de nombreux chiffres, il suffit de se rappeler comment on fait soi-même des multiplications de plusieurs chiffres alors qu’on ne sait que la table des produits de un chiffre. Ainsi, pour effectuer la multiplication de 57 × 46, on utilise la technique écrite suivante :

Cette merveilleuse technique nommée aussi italienne ou grecque qui nous vient d’Orient est utilisée au XVème siècle par le mathématicien arabe Al kasi, . Mais on la trouve beaucoup plus tôt chez les arabes aux alentours du XIIIe siècle (multiplication par le quadrillage ou par le tableau). Elle serait aussi dans un ouvrage de Fibonacci de 1202.
A la fin du Moyen-Age la technique fut surnommée « per gelosia ».
Ce nom fait allusion à la pièce en bois qui équipait certaines « fenêtres à jalousie » en Italie chez les maris jaloux. Ils voulaient bien que leur femme regarde ce qui se passe dans la rue, sans que les hommes qui s’y trouvaient puissent les voir.
Cette technique a fini par donner notre algorithme de multiplication.
Il faut écrire le multiplicande en haut et horizontalement, et le multiplicateur à droite et verticalement.
Pour les petites multiplications, on multiplie les chiffres des unités que l’on note dans la case supérieure à droite, la dizaine dans la partie supérieure de cette case, les unités dans la partie inférieure (la case est divisée en 2 par la diagonale). Et ainsi de suite.
| |
Pour les grosses multiplications, le principe est le même, mais on multiplie par classe de 3 chiffres. Voir le tableau Excel ci-contre.
Pour le résultat final, on ajoute en DIAGONALE en tenant compte des retenues additives, les résultats obtenus dans les cases et ceci de droite à gauche. |
B°/ Les très grosses divisions :
| |
Fichier Excel : grosses divisions. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online) |
C°/ La méthode mentale du rectangle : calcul mental
Voici une méthode qui va nous permettre de simplifier la plupart des multiplications de 2 nombres.
Soit la multiplication de A par B. Le but du jeu est de trouver un nombre R, proche de A et B, et qui de plus soit simple a multiplier comme un multiple de 10 par exemple.
Ainsi : A × B = ( R + a ) × ( R + b ) = R² + Rb + aR + ab = R × ( R + a + b ) + ab
L’astuce est de placer les 4 nombres sur un rectangle. Le produit de A par B devient donc la somme du produit de R ( qui est simple à multiplier ), par R + a + b ( qui l’est un peu moins s’est vrai ) et de ab.

On peut fabriquer un tour de magie assez impressionnant en améliorant cette méthode. Affirmer que vous êtes capable de multiplier très rapidement 2 nombres de 2 chiffres.
Demandez à quelqu’un de choisir un nombre à deux chiffres et proposez le deuxième. L’astuce consiste à choisir un nombre de la même dizaine et dont l’unité est le complément à 10.
Par exemple 52 et 58 car 8 = 10 – 2.
Le produit de 2 nombres sera un nombre de 4 chiffres dont les 2 premiers seront le produit du chiffre des dizaines fois son suivant, et les 2 derniers chiffres seront le produit des unités des 2 chiffres : (10d + u) x (10d + (10-u)) = d(d + 1)100 + u(10 – u).
52 x 58 = 3016 en effet : 5×6 = 30 et 2×8 = 16
La démonstration de ce prodige est assez simple : Soit (10d + u) le premier nombre alors le second sera 10d + (10-u)
(10d + u) x (10d + (10-u)) = 100d² + 100d – 10du + 10ud + 10u – u² = 100d² + 100d + 10u – u² = 100(d² + d) + u(10 – u)
= d(d + 1)100 + u(10 – u)
Avec : d = chifre des dizaines
d+1 = chiffre des dizaines suivantes
u = chiffre des unités
10 – u = complément à 10 du chiffre des unités
Exemples :
| 34 x 36 = 1224 | 3×4 = 12 | 4×6 = 24 |
| 73 x 77 = 5621 | 7×8 = 56 | 3×7 = 21 |
| 29 x 21 = 609 | 2×3 = 06 | 9×1 = 09 |
| 92 x 98 = 9016 | 9×10 = 90 | 2×8 = 16 |
Cependant votre interlocuteur peut se rendre compte de votre manipulation, alors voici une variante : il faudra prendre le second nombre pour qu’il soit le complément du premier par rapport à la dizaine la plus proche. Par exemple 52 et 48 : 52 est à 2 unités de 50 ainsi que 48 mais dans l’autre sens.
Le produit de 2 nombres dont R est la dizaine la plus proche et k les unités d’écart, sera le R² – k².
La démonstration : Soit A le premier nombre qui est au-dessus du nombre R de k unités, alors le second sera B qui est au-dessous du nombre R de k unités. On aura :
A = R + k ainsi : A x B = (R + k) x (R – k) = R² – k²
B = R – k
Exemples :
| Produit | Dizaine la plus proche R | k les unités d’écart | Détail |
| 34×26 = 884 | 30 | 4 | 30² – 4² = 900 – 16 |
| 92×88 = 8096 | 90 | 2 | 90² – 2² = 8100 – 4 |
| 56×64 = 3584 | 60 | 4 | 60² – 4² = 3600 – 16 |
D°/ Trouver le dernier chiffre d’un quotient :
Si le diviseur d’une division se termine par 1, 3, 7 ou 9, on peut trouver facilement le dernier chiffre du quotient.
| Le diviseur se termine par | Le quotient se termine par | Exemple |
|
1 |
L’unité du dividende. | 1054/31 =34 |
|
3 |
Un multiple de 3 qui se termine par l’unité du dividende. | 782/23 = 34
le seul multiple de 3 se terminant par 2 est 12 = 3 × 4 |
|
7 |
Un multiple de 7 qui se termine par l’unité du dividende. | 901/17 = 53
le seul multiple de 7 se terminant par 1 est 21 = 7 × 3 |
|
9 |
Le nombre 10 ôté de l’unité du dividende. | 986/29 = 34
10 – 6 = 4 |
E°/ Méthode manuelle pour effectuer les multiplications :
Il existe un truc infaillible pour trouver les produits de nombres strictement plus grands que 5, quand on connaît ses tables jusqu’à 5.
Il suffit de jouer avec ses doigts.
Les doigts sont numérotés de 6 à 10 à partir du pouce sur chaque main.
On fait se toucher les deux doigts correspondant aux nombres désirés.
Le nombre de doigts qui se touchent ajouté à ceux qui sont en-dessous donne des dizaines.
Le nombre de doigts du dessus à gauche multiplié par le nombre de doigts du dessus à droite, donne des unités.On ajoute alors toutes les unités obtenues.
Compliqué ? Non, regardons bien ci-dessous.



F°/ Différentes méthodes de multiplication :
F-1°/ Multiplication babylonienne (Somme de carrés en Mésopotamie):
| Près de l’Euphrate, sur le site de Nippour, proche de l’ancienne Babylone on a trouvé un grand nombre de temples datant d’environ 3000 ans avant notre ère. Sur des tablettes d’environ 1000 ans avant notre ère, on a observé une curieuse procédure pour effectuer des multiplications.
Cette technique de multiplication des entiers nécessitait uniquement de savoir faire des additions et peut-être des soustractions. Le scribe calculateur devait aussi disposer d’une table de carrés. La multiplication se ramenait à une addition de carrés. Pas très rapide ni très pratique… ce procédé repose sur le fait que tout nombre entier peut se décomposer en somme de carrés. |
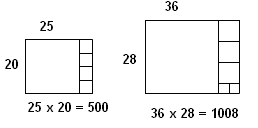
Par exemple :
25 x 20 = (20 + 5) x 20 = 20 x 20 + 5 x 20 = 20² + 5 x 5 x 4 = 20² + 4 x 5² = 400 + 4 x 25 = 500
36 x 28 = (28 + 8) x 28 = 28² + 8 x (3 x 8 + 4) = 28² + 3 x 8² + 2 x 4² = 844 + 3 x 64 + 2 x 16 = 1 008
F-2°/ Multiplication égyptienne :
Bien sûr cette multiplication des commerçants du Nil marche toujours ! Elle a l’énorme avantage de n’utiliser que la table de deux.
Pour faire 458 × 25, on effectue toutes les multiplications du multiplicande M = 458 par tous les multiples m de 2, de 20 à 2n. Il suffit de doubler les résultats à partir de la multiplication par 1, ce qui est simple.
Ensuite on cherche une somme qui donne le multiplicateur m = 25 en additionnant les multiplicateurs p de 458. En lisant Mod(M/2) en partant d’en bas, on obtient l’écriture binaire de m (25 s’écrit 11001 en binaire).
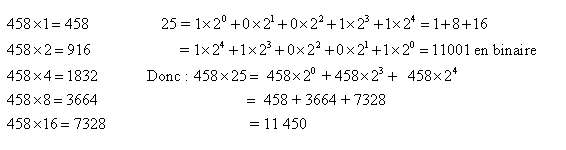
C’est long mais il ne faut maitriser que la table de 2 et l’addition. L’explication tient dans la possibilité de décomposer un nombre en somme de puissances de 2.
F-3°/ Multiplication Russe :
Cette multiplication a l’énorme avantage de n’utiliser que la table de deux. Elle très semblable à la Multiplication égyptienne.
Pour passer d’une ligne à la suivante on double le multiplicande M et divise le multiplicateur m par 2 en arrondissant à l’entier inférieur jusqu’à 1.
Tout irait parfaitement bien si les nombres étaient tous pairs…
On ajoute donc les produits de M qui sont multipliés par un m impair pour rattraper les pertes dues aux multiplications par des nombres impairs.
Plaçons 1 en face des lignes correspondant à une multiplication par un nombre impair et 0 devant les autres. Si maintenant nous relisons de bas en haut les chiffres 1 et 0, nous obtenons l’écriture binaire du nombre 25 par lequel nous avons multiplié 458. En effet 25 s’écrit 111 en binaire.

C’est long mais il ne faut maitriser que la table de 2 et l’addition. L’explication tient dans la possibilité de décomposer un nombre en somme de puissances de 2.
| |
Voici un fichier Excel pour manipuler : Multiplication Russe. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online) |
F-4°/ La multiplication per Gelosia Grecque ou Italienne :
| Cette merveilleuse technique nommée aussi italienne ou grecque qui nous vient d’Orient est utilisée au XVème siècle par le mathématicien arabe Al kasi, . Mais on la trouve beaucoup plus tôt chez les arabes aux alentours du XIIIe siècle (multiplication par le quadrillage ou par le tableau). Elle serait aussi dans un ouvrage de Fibonacci de 1202.
A la fin du Moyen-Age la technique fut surnommée « per gelosia ». Ce nom fait allusion à la pièce en bois qui équipait certaines « fenêtres à jalousie » en Italie chez les maris jaloux. Ils voulaient bien que leur femme regarde ce qui se passe dans la rue, sans que les hommes qui s’y trouvaient puissent les voir. Cette technique a fini par donner notre algorithme de multiplication. Il faut écrire le multiplicande en haut et horizontalement, et le multiplicateur à droite et verticalement. Pour les petites multiplications, on multiplie les chiffres des unités que l’on note dans la case supérieure à droite, la dizaine dans la partie supérieure de cette case, les unités dans la partie inférieure (la case est divisée en 2 par la diagonale). Et ainsi de suite. Voir l’animation « Multiplication Grecque ». Pour les grosses multiplications, le principe est le même, mais on multiplie par classe de 3 chiffres. Voir le tableau excel ci-dessous. Pour le résultat final, on ajoute en DIAGONALE en tenant compte des retenues additives, les résultats obtenus dans les cases et ceci de droite à gauche. |
F-5°/ Méthode des lignes : multiplication Japonaise
Cette technique amusante ne fait apparemment intervenir aucune table de multiplication.
On trace horizontalement et verticalement le nombre de lignes ou de colonnes correspondant au chiffre indiqué en haut ou à droite. Ensuite comme pour la technique à la grecque, il suffit de compter les points en diagonale. Les retenues éventuelles sont reportées sur la diagonale de gauche. En comptant le nombre de croix d’un rectangle de n lignes sur m colonnes, on redéfinit tout simplement la multiplication n x m.
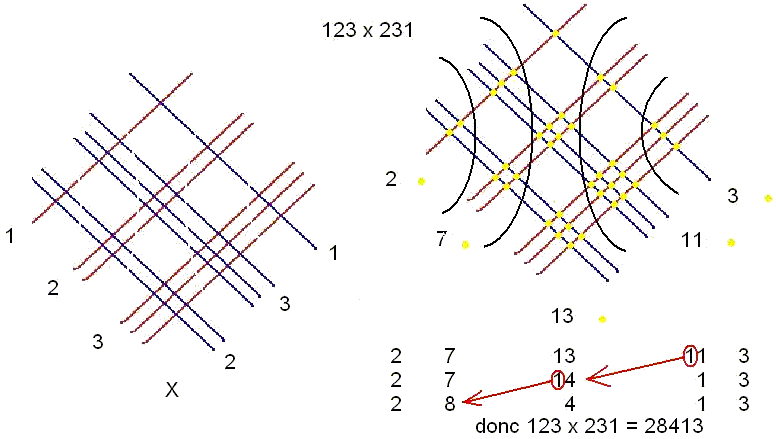
F-6°/ Méthode des cercles :
Même méthode que celle avec les traits, mais avec des cercles !!
F-7°/ Méthode des bâtons de Neper dit aussi de Napier :
John Napier, parfois francisé en Jean Neper, né le et mort le , est un théologien, physicien, astronome et mathématicien écossais.
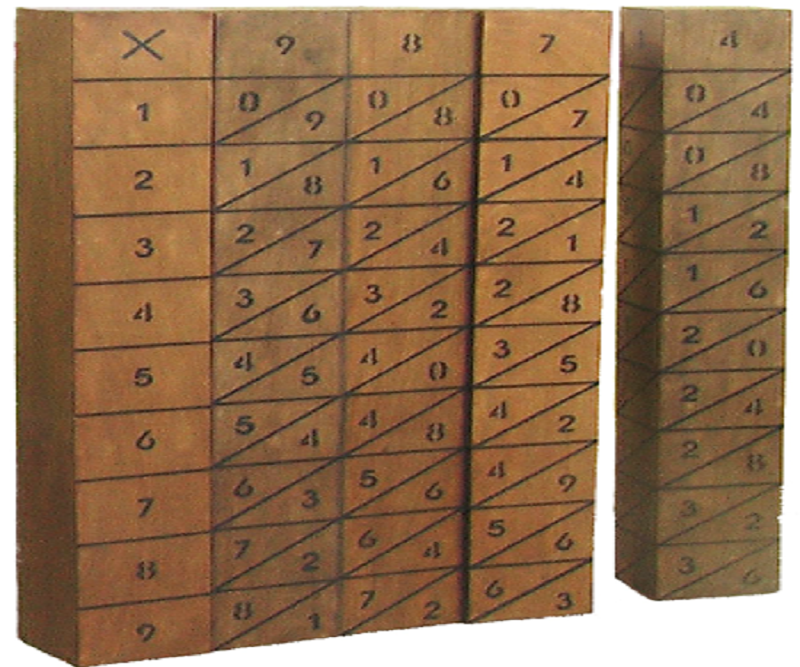
Il a inventé les bâtons de Napier, ou réglettes de Neper est un abaque facilitant le calcul des produits, quotients, puissances et racines.
 |
 |
 |
Pour la multiplication, la règle est simple :
 |
Les réglettes de Napier sont constituées d’une série de barres verticales numérotées qui représente chacune une table de multiplication; ainsi nous avons 9 réglettes déclinant les tables de 1 jusqu’à la table de 9. Ces résultats sont affichés sur des cases séparées par des diagonales, et de part et d’autre de ces diagonales, sont représentés les chiffres des dizaines et des unités. |
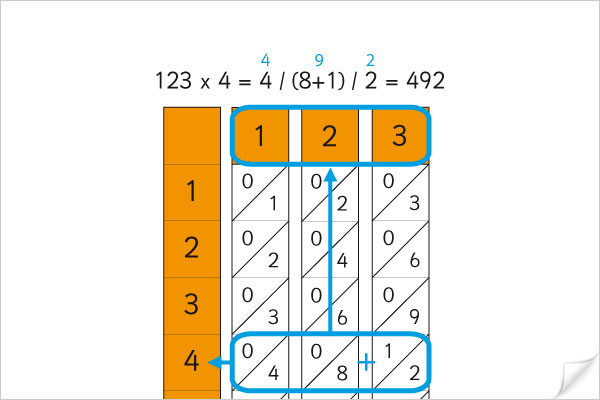 |
Ces réglettes mobiles, permettent de poser des opérations de multiplication en alignant une successions de réglettes pour composer le nombre souhaité : en alignant les réglettes 1, 2 et 3, nous considérons le nombre 123. Nous pouvons ainsi librement aligner les réglettes de notre choix pour former un nombre dans les dizaines, centaines, milliers etc…
Pour lire le résultats, il faut additionner, sur la ligne souhaitée, les chiffres en diagonale, en tenant compte des retenues , ce qui revient à des additions de chiffres simples pour obtenir le résultat.. Pour le produit 123 x 4, nous regardons la ligne 4 : nous avons ainsi (centaines = 4+0 = 4), (dizaines 8+1 = 9), (unités = 2), résultat 492 |
Voici deux petites animations qui vous permettront de vous entrainer :
G°/ Multiplication de 2 nombres proches de 100 :
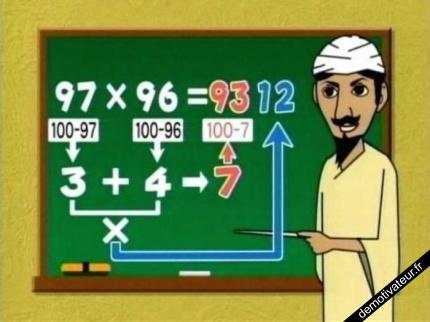
Explications :
1ier nombre = 100 – a
2ième nombre = 100 – b
(100 – a) × (100 – b) = 10 000 – 100b – 100a + ab
= 10 000 – 100(a + b) + ab
= 100[100 – (a + b)] +ab
Vérification :
97 × 96 = 9 312
(100 – 3) × (100 – 4) = 100[100 – (3+4)] + 3 × 4
= 100 × 93 + 12
= 9 312
H°/ Tables de multiplication façon modulo :
Je vais vous expliquer les tables de multiplication d’une façon tout à fait différente.
Il s’agit de visualiser les tables à l’aide de segments dans un cercle.
L’idée de base de l’arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par un nombre.
Par exemple, s’il est 16h52 et que j’attends 15 minutes, il sera 17h07, autrement dit 52+15=7 dans l’arithmétique à base 60 des minutes.
Ce que nous en écrivons, en mathématiques : 52 + 15 ≡ 7 (mod. 60) autrement dit dans 67/60 il reste 7. En effet : 67/60 = 1 et il reste bien 7.
et que nous lisons : « 52 plus 15 est congru à 7 modulo 60 ».
Pourquoi congru ? En latin, congruens signifie « qui s’accorde ».
Pourquoi modulo ? Il s’agit de l’ablatif du nom latin modulus, qui signifie « mesure ».
On peut visualiser les tables de multiplication en utilisant le modulo des nombres.
Voici une explication détaillée : Cliquez sur l’image pour lancer la vidéo ou le programme.
| Superbe vidéo de Mickaël Launay de sa chaine Youtube. | Programme Scratch qui explique tout. |
 |
|
|
|
I°/ Des simplifications bizarres :
Pour simplifier des fractions la règle est simple. Il faut diviser le numérateur et le dénominateur par le même nombre.
\frac{15}{21} = \frac{\cancel{3}\times 5}{\cancel{3}\times 7}=\frac{5}{7}Il y a bien quelques élèves qui comprennent que l’on peut éliminer le même chiffre en « haut » et en « bas » et qui se permettent d’écrire :
\frac{15}{21} = \frac{\cancel{1}5}{2 \cancel{1}}=\frac{5}{2} Mais c’est totalement faux.
Quoiqu’il existe des cas où cela fonctionne :
| Simplifications correctes | Simplifications alternatives (mais toujours illégales !!) |
| \frac{16}{64} = \frac{\cancel{16}\times 1}{\cancel{16}\times 4}=\frac{1}{4} | \frac{16}{64} = \frac{1 \cancel{6}}{ \cancel{6} 4}=\frac{1}{4} |
| \frac{26}{65} = \frac{\cancel{13}\times 2}{\cancel{13}\times 5}=\frac{2}{5} | \frac{26}{65} = \frac{2 \cancel{6}}{ \cancel{6} 5}=\frac{2}{5} |
| \frac{19}{95} = \frac{\cancel{19}\times 1}{\cancel{19}\times 5}=\frac{1}{5} | \frac{19}{95} = \frac{1 \cancel{9}}{ \cancel{9} 5}=\frac{1}{5} |
Pourvu que mes élèves ne tombent pas sur cet article, ce sera la révolution dans la classe !!!
J°/ Décomposition en facteur premiers :
Voici une très belle animation qui montre visuellement la décomposition des nombres en facteurs premier.
K°/ La notation Polonaise :
Nous sommes parfois si habitués à certaines conventions humaines que nous finissons par en oublier que nous aurions pu faire autrement. Ainsi, notre façon d’écrire un calcul aussi simple que 1 + 1 n’a rien d’obligatoire.
L’une des plus fameuses alternatives se nomme « la notation polonaise » et fut inventée en 1924 par le mathématicien (polonais) Jan Łukasiewicz. Dans ce système, l’addition précédente se note « + 1 1 ». Autrement dit, le symbole d’opération ne vient pas se placer entre les deux nombres, mais avant eux. De la même façon, le calcul que nous notons « 2 × (3 + 4) » se notera « × 2 + 3 4 » en notation polonaise.
L’intérêt principal de cette méthode est lever toute ambiguïté sur l’ordre dans lequel effectuer les opérations et de rendre obsolète l’usage des parenthèses.
Mais avec l’apparition des ordinateurs, une variante de la notation Polonaise a vu le jour : la notation Polonaise inversée ou NPI. Les opérations seront à présent écrites après les nombres. Pour ne pas confondre 3 + 4 avec 34 il faudra laisser un espace entre les deux chiffres ou faire « Enter » sur une machine à calculer (symboliser par ↑ ).
| Calculs conventionnels | Notation Polonaise | Notation Polonaise inversée |
| 1 + 1 = 2 | + 1 ↑ 1 | 1 ↑ 1 + |
| 2 × (3 + 4) = 14 | × 2 + 3 ↑ 4 | 2 ↑ 3 ↑ 4 x + |
| (2 + 1) × (6 – (4 × 2)) = -6 | × + 2 ↑ 1 − 6 × 4 ↑ 2 | 2 ↑ 1 + 6 ↑ 4 ↑ 2 x – x |
Voici un site pour expérimenter cette NPI ou alors une calculatrice NPI.