X°/ Des bouliers à l’informatique :

Visiteurs : 209

I°/ Les bouliers :
II°/ L’Algorithmique :
III°/ L’informatique :
IV°/ Le Binaire :
     1°/ Histoire :
     2°/ Utilisation du binaire : 2 chiffres suffisent à coder
     3°/ Les unités :
     4°/ Tables de code :
     5°/ L’algèbre de Boole :

I°/ Les bouliers :

L’histoire du boulier remonte à 2500 ou 3000 ans. Les savants chinois effectuaient les 4 opérations arithmétiques grâce à un abaque nommé Chou suan, ancêtre de l’actuel boulier nommé Suan pan. Ce fut sans doute l’un des premiers systèmes de calcul inventé. Le Chouan suan représentait les nombres grâce à la numération de position qui nous est si familière aujourd’hui.

Il existe actuellement trois types de bouliers, le boulier chinois, le boulier japonais et le boulier russe.

Une vidéo qui explique bien le fonctionnement des bouliers : ICI

Une autre sur les machines à calculer du siècle dernier, tout à fait prodigieuses et qui fonctionnaient sans piles : ICI

Le boulier chinois :		Le boulier chinois est formé de tiges séparées en deux par une barre transversale : la partie inférieure compte 5 boules d’une unité, la partie supérieure 2 boules de 5 unités. Chaque tige correspond, de droite à gauche, respectivement aux unités, dizaines, centaines, milliers etc.. Lorsque ce boulier est passé au Japon, les Japonais ont réalisé que la 5ème boule du bas et la 2ème boule du haut étaient inutiles. Ils l’ont donc simplifié vers 1945.
Le boulier japonais :		Le boulier japonais (*Soroban*) ne compte qu’une rangée de boules à section hexagonale en haut et 4 en bas. Il tend à se répandre partout dans le monde, même en Chine. La partie inférieure compte 4 boules d’une unité, la partie supérieure 1 boule de 5 unités.
Le boulier russe :		Le boulier russe comporte 10 boules enfilées sur des tiges.

Le boulier de 10 boules a été employé dans les écoles communales françaises au XIXe siècle pour apprendre à calculer. Pour les opérations sur le boulier, il suffit de connaître par cœur les tables d’addition et des multiplication des nombres de 1 à 9 .
La numération de position permet d’écrire de façon simple de grands nombres avec peu de symboles. Elle est très efficace. Avec la numération de position, on a convenu d’écrire les nombres en commençant par le chiffre de rang le plus élevé. Mais pour lire un nombre on doit donc noter ce rang immédiatement. Il faut donc repérer, plus à droite, la position du chiffre des unités ! C’est pour cela que nous faisons des paquets de trois chiffres à partir des unités. Cet inconvénient disparaît sur le boulier.
Le boulier s’utilise à plat sur un plan horizontal. On ne prend en compte que les boules qui sont près de la barre centrale. Le nombre de chiffres d’un nombre correspond au nombre de tiges : de droite à gauche on a les unités puis les dizaines, puis les centaines etc.. Si l’on doit calculer avec une virgule, on repousse la rangée des unités aussi loin que l’inscription des chiffres après la virgule le nécessite.

Les boules du haut valent 5 unités et celles du bas 1 unité (comme pour le chinois). Seules les boules près de la barre centrale sont prises en compte. Les nombres se lisent de gauche à droite. Pour additionner, on procèdera de gauche à droite.

Choisir l’écriture d’un nombre ou l’addition pas à pas de deux nombres. L’inscription ou l’opération se fera, pas à pas, en cliquant sur le bouton fléché.	Exercez-vous à écrire avec le boulier. Un nombre est proposé il faut le composer sur le boulier en cliquant les boules adéquates. On peut les monter ou les descendre une par une ou bien plusieurs à la fois. Quand c’est fait cliquer sur OK. Quand l’aide est activée, le nombre construit sur le boulier s’affiche au fur et à mesure des clics sur les boules.

Voici une d’autres animations pour utiliser des bouliers :

Sur le plan pratique on ne travaille qu’avec 3 doigts.

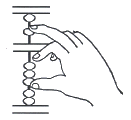L’addition et la soustraction s’effectuent de gauche à droite.
Ainsi pour ajouter 56 à 140, on ajoutera d’abord les dizaines (5 dizaines) puis les 6 unités.
L’addition est un problème de positionnement et de gymnastique mentale.

On peut faire un nombre de différente façon. Par exemple, pour ajouter 4 :

– on le fait directement si les boules sont disponibles.

– on abaisse une du haut (+5) et on abaisse une du bas (-1) : 5 – 1 = 4

– on soulève en même temps une du haut (-5) et une boule de la tige suivante (+10) et on abaisse une boule du bas (-1) d’où 10 – 5 – 1 = 10 – 6 = 4

La soustraction : Opération inverse de l’addition, la soustraction à l’aide du boulier consiste à poser le premier membre de la soustraction et à retirer les boules correspondant au second membre de l’opération. La soustraction s’effectue en partant de la gauche du boulier, sur le plus grand des deux nombres.

La multiplication : La multiplication est l’opération qui consiste à additionner le multiplicande autant de fois que l’indique le multiplicateur afin d’obtenir le résultat appelé produit. Pour faire une multiplication avec un boulier, on écrit le multiplicateur à gauche et le multiplicande à droite laissant autant de colonnes libres que le multiplicateur comprend de chiffres.

exemple : 123 X 4

1) 4 X 3 = 12

2) 4 X 20 = 80 que l’on ajoute à 12

3) 4 X 100 = 400 que l’on ajoute à 92

La division : La division est l’opération inverse de la multiplication, qui consiste à soustraire le diviseur du dividende autant de fois qu’on le pourra. Le résultat de l’opération ou quotient représente le nombre de fois que l’on a le diviseur dans le dividende. C’est un exercice très délicat sur le boulier, qui demande une parfaite maîtrise des trois autres opérations.

D’abord on place le diviseur à gauche et le dividende à droite et l’opération terminée, le quotient prend la place du dividende et le reste la dernière colonne à droite.

Prenons la division, 186 / 6 = 31

1) 1 / 6 => 10 / 6 = 1 reste 4 à ajouter au chiffre suivant 8

2) 12 / 6 = 2 que l’on ajoute à la colonne précédente

3) 6 / 6 = 1 que l’on ajoute à la colonne précédente

II°/ L’Algorithmique :

L’algorithmique c’est l’art de découper un problème complexe en tâches élémentaires.

En effet, pour faire accomplir quelque chose d’à peu près utile au tas de ferraille que vous appelez un robot sophistiqué, il est inutile de compter sur son esprit d’initiative. Au contraire, il faut tout lui expliquer correctement. Et en détail. Patiemment. Car, malgré les apparences, l’ordinateur le plus sophistiqué n’a pas beaucoup plus d’intelligence qu’une ancienne machine à coudre. Et à pédales encore !

Le mot « algorithme » vient du nom du mathématicien Al-Khwârizmî (latinisé au Moyen Âge en Algoritmi), qui, au IX^e siècle écrivit le premier ouvrage systématique donnant des solutions aux équations linéaires et quadratiques.

Voici 2 vidéos très instructives :

Un jeune chasseur du néolithique apprend avec son père à fabriquer une hache à partir de bois, de silex et d’os. Tout doit être exécuté à la perfection, dans un ordre précis. Mais aujourd’hui, nous utilisons des machines qui travaillent à notre place en obéissant à un programme spécifique. Cet épisode revient sur les étapes qui ont permis à l’être humain de découvrir et maîtriser les algorithmes.

En 1843, sur la machine à calculer de Charles Babbage, Ada Lovelace fabrique ce qui est considéré comme le tout premier programme informatique au temps où les ordinateurs n’existaient pas.
En utilisant des fiches perforées à la manière d’un orgue de barbarie, cette machine était capable d’effectuer des calculs élémentaires mais aussi et surtout des boucles de calcul à l’instar de nos ordinateurs. Ada Lovelace pu ainsi calculer les nombres de Bernoulli à partir du nombre B₃.

III°/ L’informatique :

L’homme a toujours chercher à automatiser les tâches du quotidien, quelles soient physiques ou intellectuelles.

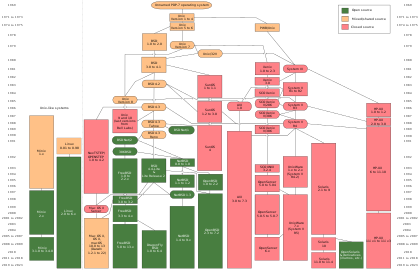
Il a inventé la parole puis l’écriture, le calcul puis les algorithmiques, les machines à calculer puis les ordinateurs. Voici une chronologie de ces inventions.

Date	Nom	Visuel	Inventeur	Principe	Principes et Stockage
-2000	Le boulier		Mésopotamie	Billes qui permettent de compter.	Principe : billes Stockage : Aucun
IX^ième siècle	Algorithmique		Al-Khwârizmî	Un algorithme est une suite finie et non ambiguë d’instructions et d’opérations permettant d’effectuer une action.	Principe : billes Stockage : Parchemin
1642	La Pascaline		Blaise Pascal	Machine capable d’additionner et de soustraire. Elle est créée spécifiquement pour le père de Blaise Pascal, qui était percepteur d’impôts.	Principe : Engrenage Stockage : Aucun
1673	La machine à calculer REPLICA de Leibniz		Gottfried Wilhelm Leibniz	Leibniz qui s’est inspiré de la Pascaline invente une machine capable de multiplier et de diviser.	Principe : Engrenage Stockage : Aucun
1800	Le métier à tisser Jacquard		Joseph Marie Jacquard	Un métier à tisser qui utilise des cartons perforés pour commander les mouvements des aiguilles. C’est la première machine programmée.	Principe : Les cartes perforée Stockage : Les cartes perforées
1834	La machine à calculer de Charles Babbage		Charles Babbage	S’inspire du métier à tisser de Jacquard, pour élaborer une machine qui, à l’aide de cartes perforées, évalue les différentes fonctions (addition, soustraction, multiplication, et division).	Principe : Les cartes perforée Stockage : Les cartes perforées
1843	Le premier programme informatique d’Ada Lovelace		Ada Lovelace	Fille du célèbre Lord Byron, un des plus grands poètes anglais de son temps, elle développe les principes de base de la programmation en travaillant avec Charles Babbage sur sa machine.	Principe : Les cartes perforée Stockage : Les cartes perforées
1936	La Bombe d’Alan Turing		Alan Turing	Il publie en 1936 un article “On Computable Numbers” définissant les bases théoriques de la programmation sur des machines capables d’effectuer des calculs. Il parvient en 1940 à “cracker” la machine de cryptage nazi appelée Enigma.	Principe : Engrenage et tube à vide Stockage : Aucun
1938-1941	Les Z1, Z2 et Z3 de Konrad Zuse		Konrad Zuse	Premier ordinateur programmable qui utilise le binaire : le Z1. C’est le premier calculateur programmable fonctionnel. Le Z3 achevé en 1941 est plus fiable que les précédentes versions.	Principe : Les cartes perforée Stockage : Les cartes perforées
1943	Le MARK 1		Howard Aiken	Créé en collaboration avec IBM c’est le premier calculateur électromécanique ASCC (Automatic Sequence Controlled Calculator). Installé à d’Harvard, il pèse 5 tonnes et 17 m de long pour 2,5 m de hauteur. Il calcule 5 fois plus vite que l’Homme de façon entièrement automatisée.	Principe : tube de Williams Stockage : Programme
1945	L’ENIAC		John William Mauchly et J. Presper Eckert	Premier ordinateur ne comportant plus aucune pièce mécanique. Il est composé de 18 000 tubes à vide, s’étend sur plus 160 m² et opère en décimal. Il est surtout utilisé pour effectuer des calculs balistiques.	Principe : Tubes à vide Stockage : Programme
1946	L’EDVAC		John von Neumann	L’EDVAC (Electronic Discrete Variable Automatic Computer) est une évolution de l’ENIAC. Il permet la mémorisation de 5,5 kilo octets et opère en binaire. Il est composé de 6 000 tubes à vide, 12 000 diodes et s’étend sur plus 45 m².	Principe : Tubes à vide et diodes Stockage : Programme
1948	Le transistor		John Bardeen, William Shockley et Walter Brattain	Il révolutionne l’informatique, permettant ainsi de fabriquer des ordinateurs moins encombrants en consommant moins d’électricité. Il s’agit d’une sorte d’interrupteur électronique automatique qui remplace les tubes à vide.
1951	Création du langage informatique par Grace hopper		Grace hopper	Après avoir travaillé sur le Mark 1, elle développe le premier compilateur sur une évolution de l’EDVAC : l’UNIVAC. Un compilateur est un système qui traduit automatiquement le langage des informaticiens en langage machine.
1962	Apparition du mot “informatique”		Philippe Dreyfus	Bien qu’étymologiquement le mot « informatik » fût créé par l’ingénieur allemand Karl Steinbuch en 1957, il est le premier à utiliser sa traduction française « informatique » dès 1962, par la fondation de la Société d’informatique appliquée (SIA). Le mot informatique désigne alors la contraction des mots information et automatique.
1963	La première souris par Doug-Engelbart		Doug-Engelbart	Mise au point au Stanford Research Institute. Elle est équipée de deux roues fixées sur deux capteurs et d’un bouton poussoir. La souris est améliorée par Jean-Daniel Nicoud dès 1979 avec une boule et deux capteurs internes ainsi que deux boutons poussoirs.
1965	Programma 101, premier ordinateur personnel d’Olivetti		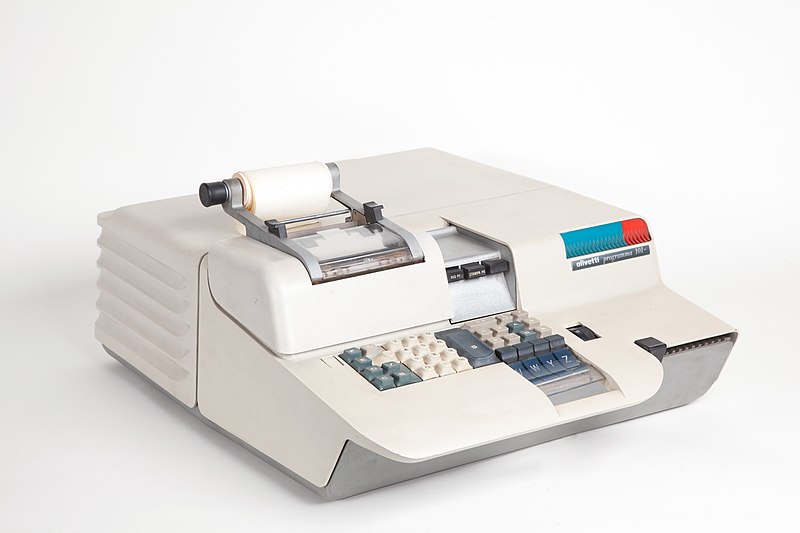Pier Giorgio Perotto	le Programma 101 de la société italienne Olivetti est le premier ordinateur personnel numérique et programmable.	Principe : Le transistor Stockage : Programme
1969	UNIX		Ken Thompson	Ken Thompson développe la première version d’un système d’exploitation en ligne de commande (UNIX).	Principe : Le transistor Stockage : Programme
1971	Premier microprocesseur		Intel	La société Intel commercialise son premier microprocesseur, le 4004.	Principe : Le transistor Stockage : Programme
1973	Premier système d’exploitation graphique		XEROX	La société XEROX sort en 1973 sa station de travail Alto équipée d’un système d’exploitation appelé Alto OS. Il possède la première barre d’outils.	Principe : Le transistor Stockage : Programme
1976	Premier ordinateur Apple		Steve Jobs, Steve Wozniak et Ronald Wayne	Premier ordinateur Apple.	Principe : Le transistor Stockage : Programme
1981	Premier PC		IBM	IBM lance le PC (Personal Computer). Son succès repose sur sa compatibilité logicielle. Quelle que soit la marque de l’ordinateur, les logiciels pour PC sont compatibles. La société Microsoft de Bill Gates, fondée en 1975 distribue rapidement des logiciels d’application (traitement de texte, gestion de base de données, etc.)	Principe : Le transistor Stockage : Programme
1984	Premier GUI sur Macintosh		Apple	les systèmes Macintosh d’Apple Computer sont les premiers à être dotés d’une interface graphique : Lisa OS. Au lieu d’avoir à taper des lignes de commandes au clavier, l’utilisateur peut maintenant se servir d’une souris et cliquer sur des icones. Le contenu est présenté sous la forme WYSIWYG “What You See Is What You Get”.	Principe : Le transistor Stockage : Programme
1985	Microsoft Windows 1.0		Microsoft	Après le succès de ses logiciels sur PC et de son système d’exploitation MS-DOS, Microsoft lance Microsoft Windows 1.0	Principe : Le transistor Stockage : Programme
1991	Linux		Linus Torvalds et Richard Stallman	Le concept consiste à développer un système d’exploitation libre et open source. Plusieurs distributions apparaissent comme Debian ou Ubuntu.	Principe : Le transistor Stockage : Programme

Liste des systèmes d’exploitation : de la naissance de l’écriture au langage informatique.

IV°/ Le Binaire :

     1°/ Histoire :
     2°/ Utilisation du binaire : 2 chiffres suffisent à coder
     3°/ Les unités :
     4°/ Tables de code :
     5°/ L’algèbre de Boole :

1°/ Histoire :

IX^e siècle av. J.-C. en Chine : Le système binaire du Yi Jing , un texte dédié à la divination, est basé sur la dualité du yin et du yang.
Environ V^e – II^e siècles av. J.-C. : Le savant indien Pingala a développé un système binaire pour décrire la prosodie dans son Chandashutram.
Les tambours à fente avec sons binaires étaient utilisés pour coder les messages en Afrique et en Asie
avant 1450 : Les habitants de l’île de Mangareva en Polynésie française utilisaient un système hybride décimal-binaire.
1605 : Francis Bacon discuta d’un système selon lequel les lettres de l’alphabet pourraient être réduites à des séquences de chiffres binaires.
1847, George Boole publia un article intitulé « L’analyse mathématique de la logique » qui décrit un système algébrique de la logique, désormais appelé algèbre de Boole. Le système de Boole était basé sur une approche binaire, un oui-non, on-off qui comprenait les trois opérations les plus élémentaires: ET, OU et NON. Ce système ne fut pas utilisé et fut oublié.
1689 : Le système de numération binaire moderne, base du code binaire, a été inventé par Gottfried Leibniz en 1689 et apparaît dans son article Explication de l’Arithmétique Binaire en 1703.
1937 : Claude Shannon se rend compte que l’algèbre booléenne qu’il avait apprise était semblable à un circuit électrique. La thèse de Shannon devint un point de départ pour l’utilisation du code binaire dans des applications pratiques telles que les ordinateurs, les circuits électriques, etc.

2°/ Utilisation du binaire : 2 chiffres suffisent à coder

Système	Système	Non	Oui
Binaire	Le bit	0	1
Métier à tisser	Une carte perforée	Trou	Plein
Informatique	Transistor	Le courant ne passe pas	Le courant passe

Le bit porte ce nom car il signifie en anglais « binary digit », ce que l’on pourrait traduire par unité binaire. Autrement dit, un chiffre ou un symbole qui représente un des deux états du code binaire. Un bit = 2 possibilités (0 ou 1). Deux bits = 4 états ou possibilités (00 / 11 / 01 / 10). Et ainsi de suite.

Plus les séries de bits (octets) sont longues, plus le nombre de combinaisons possibles augmente :
[1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1]₍₂₎= 1×2¹⁰+ 1×2⁹+ 1×2⁸ + 1×2⁷+ 1×2⁶ + 0×2⁵ + 0×2⁴ + 1×2³ + 0×2²+ 0×2¹+ 1 ×2⁰= 11111001001

3°/ Les unités :

Unités	Valeurs	Unités	Valeurs
bit	0 ou 1	Mega-octet (Mo)	10⁶ octets
byte	de 6 à 9 bit	Giga-octet (Go)	10⁹ octets
Octet (o)	8 bits = 2⁸ nombres = 256	Tera-octet (To)	10¹² octets
Kilo-octet (ko)	1000 octets

4°/ Tables de code :

Les 128 premiers caractères (de 0 à 127) représentent le code ASCII sur 7 bits = 2⁷= 128, les 128 autres le code ASCII étendu sur 8 bits = 2⁸ = 256.

code ASCII :

Déc	Oct	Héx	Binaire	Carac	Signification
0	0	00	00000000	NUL	Caractère Null
1	1	01	00000001	SOH	Début d’en-tête (Start of header)
2	2	02	00000010	STX	Début du texte (Start of Text)
3	3	03	00000011	ETX	Fin du texte (End of Text)
4	4	04	00000100	EOT	Fin de transmission (End of Transmission)
5	5	05	00000101	ENQ	Demande, fin de ligne (Enquiry, End of Line)
6	6	06	00000110	ACK	Accusé de réception (Acknowledge)
7	7	07	00000111	BEL	Caractère d’appel (Bell)
8	10	08	00001000	BS	Espacement arrière (Backspace)
9	11	09	00001001	HT	Tabulation horizontale (Horizontal Tab)
10	12	0A	00001010	LF	Saut de ligne (Line Feed)
11	13	0B	00001011	VT	Tabulation verticale (Vertical Tab)
12	14	0C	00001100	FF	Saut de page (Form Feed)
13	15	0D	00001101	CR	Retour chariot (Carriage Return)
14	16	0E	00001110	SO	Fin d’extension (Shift Out)
15	17	0F	00001111	SI	Démarrage d’extension (Shift In)
16	20	10	00010000	DLE	Échappement de lien de donnée (Data Link Escape)
17	21	11	00010001	DC1	Contrôle de périphérique de 1 à 4 (Device Control)
18	22	12	00010010	DC2
19	23	13	00010011	DC3
20	24	14	00010100	DC4
21	25	15	00010101	NAK	Accusé de réception négatif (Negative Acknowledge)
22	26	16	00010110	SYN	Attente synchronisée(Synchronous Idle)
23	27	17	00010111	ETB	Fin du bloc de transmission (End of Transmission Block)
24	30	18	00011000	CAN	Annulation (Cancel)
25	31	19	00011001	EM	Fin de support (End of Medium)
26	32	1A	00011010	SUB	Substitution (Substitute)
27	33	1B	00011011	ESC	Échappement (Escape)
28	34	1C	00011100	FS	Séparateur de fichier (File Separator)
29	35	1D	00011101	GS	Séparateur de groupe (Group Separator)
30	36	1E	00011110	RS	Séparateur d’enregistrement (Record Separator)
31	37	1F	00011111	US	Séparateur d’unité (Unit Separator)
32	40	20	00100000	SP	Espace
33	41	21	00100001	!
34	42	22	00100010	«
35	43	23	00100011	#
36	44	24	00100100	$
37	45	25	00100101	%
38	46	26	00100110	&
39	47	27	00100111	‘
40	50	28	00101000	(
41	51	29	00101001	)
42	52	2A	00101010	*
43	53	2B	00101011	+
44	54	2C	00101100	,
45	55	2D	00101101	–
46	56	2E	00101110	.
47	57	2F	00101111	/
48	60	30	00110000	0
49	61	31	00110001	1
50	62	32	00110010	2
51	63	33	00110011	3
52	64	34	00110100	4
53	65	35	00110101	5
54	66	36	00110110	6
55	67	37	00110111	7
56	70	38	00111000	8
57	71	39	00111001	9
58	72	3A	00111010	:
59	73	3B	00111011	;
60	74	3C	00111100	<
61	75	3D	00111101	=
62	76	3E	00111110	>
63	77	3F	00111111	?
64	100	40	01000000	@
65	101	41	01000001	A
66	102	42	01000010	B
67	103	43	01000011	C
68	104	44	01000100	D
69	105	45	01000101	E
70	106	46	01000110	F
71	107	47	01000111	G
72	110	48	01001000	H
73	111	49	01001001	I
74	112	4A	01001010	J
75	113	4B	01001011	K
76	114	4C	01001100	L
77	115	4D	01001101	M
78	116	4E	01001110	N
79	117	4F	01001111	O
80	120	50	01010000	P
81	121	51	01010001	Q
82	122	52	01010010	R
83	123	53	01010011	S
84	124	54	01010100	T
85	125	55	01010101	U
86	126	56	01010110	V
87	127	57	01010111	W
88	130	58	01011000	X
89	131	59	01011001	Y
90	132	5A	01011010	Z
91	133	5B	01011011	[
92	134	5C	01011100	\
93	135	5D	01011101	]
94	136	5E	01011110	^
95	137	5F	01011111	_
96	140	60	01100000	`
97	141	61	01100001	a
98	142	62	01100010	b
99	143	63	01100011	c
100	144	64	01100100	d
101	145	65	01100101	e
102	146	66	01100110	f
103	147	67	01100111	g
104	150	68	01101000	h
105	151	69	01101001	i
106	152	6A	01101010	j
107	153	6B	01101011	k
108	154	6C	01101100	l
109	155	6D	01101101	m
110	156	6E	01101110	n
111	157	6F	01101111	o
112	160	70	01110000	p
113	161	71	01110001	q
114	162	72	01110010	r
115	163	73	01110011	s
116	164	74	01110100	t
117	165	75	01110101	u
118	166	76	01110110	v
119	167	77	01110111	w
120	170	78	01111000	x
121	171	79	01111001	y
122	172	7A	01111010	z
123	173	7B	01111011	{
124	174	7C	01111100	\|
125	175	7D	01111101	}
126	176	7E	01111110	~
127	177	7F	01111111	DEL	Supprimer

code ASCII étendu :

ASCII	Octal	Hexadécimal	Binaire	Caractère (ANSI)
128	200	80	10000000	€
129	201	81	10000001
130	202	82	10000010	‚
131	203	83	10000011	ƒ
132	204	84	10000100	„
133	205	85	10000101	…
134	206	86	10000110	†
135	207	87	10000111	‡
136	210	88	10001000	ˆ
137	211	89	10001001	‰
138	212	8A	10001010	Š
139	213	8B	10001011	‹
140	214	8C	10001100	Œ
141	215	8D	10001101
142	216	8E	10001110	Ž
143	217	8F	10001111
144	220	90	10010000
145	221	91	10010001	‘
146	222	92	10010010	’
147	223	93	10010011	“
148	224	94	10010100	”
149	225	95	10010101	•
150	226	96	10010110	–
151	227	97	10010111	—
152	230	98	10011000
153	231	99	10011001	™
154	232	9A	10011010	š
155	233	9B	10011011	›
156	234	9C	10011100	œ
157	235	9D	10011101
158	236	9E	10011110	ž
159	237	9F	10011111	Ÿ
160	240	A0	10100000
161	241	A1	10100001	¡
162	242	A2	10100010	¢
163	243	A3	10100011	£
164	244	A4	10100100	¤
165	245	A5	10100101	¥
166	246	A6	10100110	¦
167	247	A7	10100111	§
168	250	A8	10101000	¨
169	251	A9	10101001	©
170	252	AA	10101010	ª
171	253	AB	10101011	«
172	254	AC	10101100	¬
173	255	AD	10101101
174	256	AE	10101110	®
175	257	AF	10101111	¯
176	260	B0	10110000	°
177	261	B1	10110001	±
178	262	B2	10110010	²
179	263	B3	10110011	³
180	264	B4	10110100	´
181	265	B5	10110101	µ
182	266	B6	10110110	¶
183	267	B7	10110111	·
184	270	B8	10111000	¸
185	271	B9	10111001	¹
186	272	BA	10111010	º
187	273	BB	10111011	»
188	274	BC	10111100	¼
189	275	BD	10111101	½
190	276	BE	10111110	¾
191	277	BF	10111111	¿
192	300	C0	11000000	À
193	301	C1	11000001	Á
194	302	C2	11000010	Â
195	303	C3	11000011	Ã
196	304	C4	11000100	Ä
197	305	C5	11000101	Å
198	306	C6	11000110	Æ
199	307	C7	11000111	Ç
200	310	C8	11001000	È
201	311	C9	11001001	É
202	312	CA	11001010	Ê
203	313	CB	11001011	Ë
204	314	CC	11001100	Ì
205	315	CD	11001101	Í
206	316	CE	11001110	Î
207	317	CF	11001111	Ï
208	320	D0	11010000	Ð
209	321	D1	11010001	Ñ
210	322	D2	11010010	Ò
211	323	D3	11010011	Ó
212	324	D4	11010100	Ô
213	325	D5	11010101	Õ
214	326	D6	11010110	Ö
215	327	D7	11010111	×
216	330	D8	11011000	Ø
217	331	D9	11011001	Ù
218	332	DA	11011010	Ú
219	333	DB	11011011	Û
220	334	DC	11011100	Ü
221	335	DD	11011101	Ý
222	336	DE	11011110	Þ
223	337	DF	11011111	ß
224	340	E0	11100000	à
225	341	E1	11100001	á
226	342	E2	11100010	â
227	343	E3	11100011	ã
228	344	E4	11100100	ä
229	345	E5	11100101	å
230	346	E6	11100110	æ
231	347	E7	11100111	ç
232	350	E8	11101000	è
233	351	E9	11101001	é
234	352	EA	11101010	ê
235	353	EB	11101011	ë
236	354	EC	11101100	ì
237	355	ED	11101101	í
238	356	EE	11101110	î
239	357	EF	11101111	ï
240	360	F0	11110000	ð
241	361	F1	11110001	ñ
242	362	F2	11110010	ò
243	363	F3	11110011	ó
244	364	F4	11110100	ô
245	365	F5	11110101	õ
246	366	F6	11110110	ö
247	367	F7	11110111	÷
248	370	F8	11111000	ø
249	371	F9	11111001	ù
250	372	FA	11111010	ú
251	373	FB	11111011	û
252	374	FC	11111100	ü
253	375	FD	11111101	ý
254	376	FE	11111110	þ
255	377	FF	11111111	ÿ

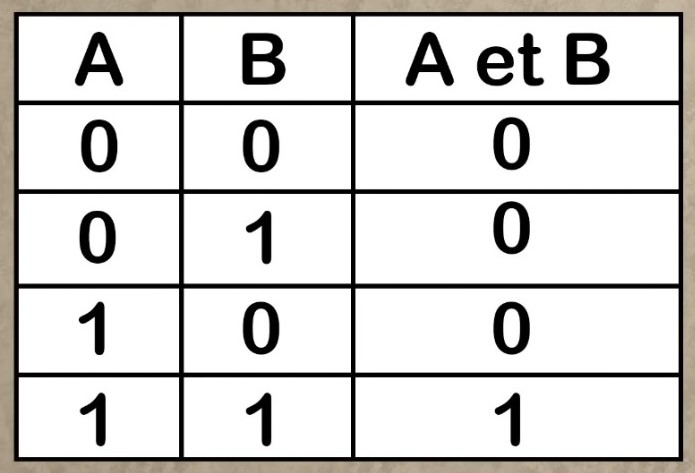
5°/ L’algèbre de Boole :

Posséder des caractères c’est bien pour créer un vocabulaire mais c’est insuffisant pour effectuer des opérations et des commandes logiques. Il faut bien se rappeler que l’on n’a que 2 actions possibles. George Boole développe une nouvelle forme de logique, à la fois symbolique et mathématique. Le but : traduire des idées et des concepts en équations, leur appliquer certaines lois et retraduire le résultat en termes logiques. Pour cela, il crée une algèbre binaire, dite booléenne, n’acceptant que deux valeurs numériques : 0 et 1. Cette algèbre est définie par la donnée d’un ensemble E (non vide) muni de deux lois de composition interne (le ET et le OU) satisfaisant à un certain nombre de propriétés (commutativité, distributivité…).


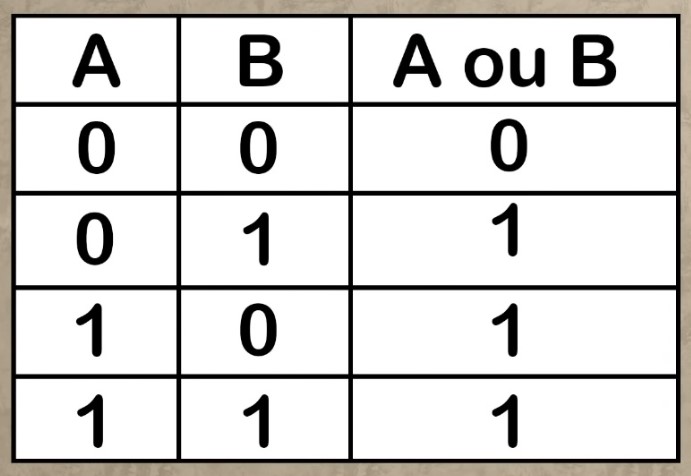Voici comment traduire une commande ET entre 2 action A et B.	Voici comment traduire une commande OU entre 2 action A et B.

Un site pour comprendre toute l’algèbre de Boole.