I°/ Solide 3D :
II°/ La Géométrie non Euclidienne :
III°/ La cartographie :
1°/ Les cartes de la terre au fil des âges :
2°/ Longitude et latitude :
3°/ Représentations des cartes modernes :
IV°/ L’Everest est-il le plus haut sommet ?
I°/ Solide 3D :
Des sites pour visualiser les solides en 3D.
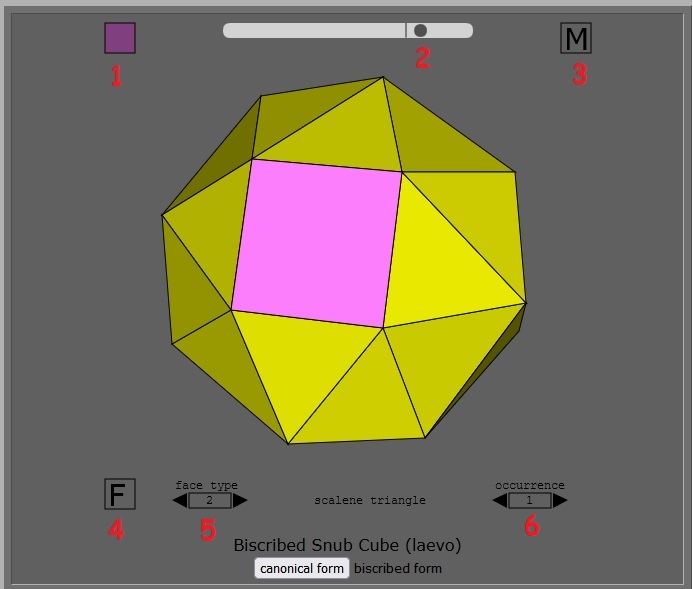 |
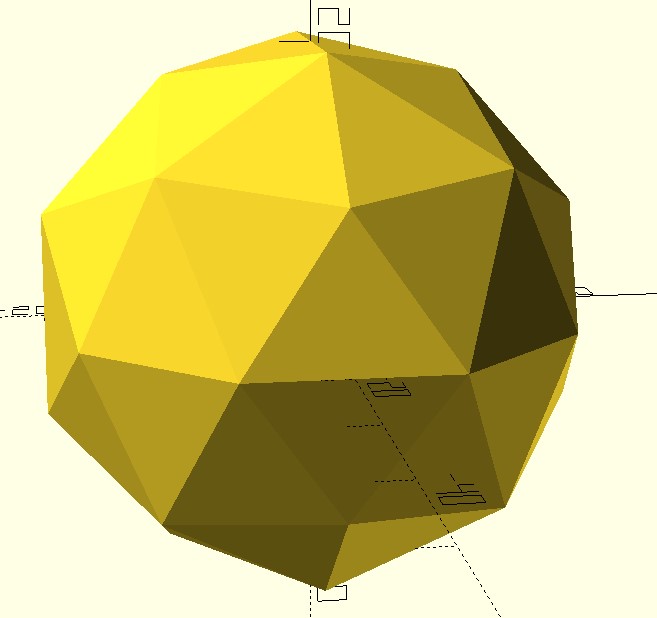
Un site pour voir des figures en 3D et les faire bouger : http://dmccooey.com/polyhedra/ Bartholomew’s Regional Projection la souris et en la déplaçant, on peut faire bouger le solide. |
 |
|
II°/ La Géométrie non Euclidienne :
La géométrie Euclidienne est basée sur les axiomes et postulats posés par Euclide dans les Éléments. Un axiome est une proposition non démontrée considérée comme évidente et qui sert de fondement à un raisonnement.
Dans la géométrie non euclidienne on écarte le postulat des parallèles. Ce postulat des parallèles dit que si deux lignes droites sont sécantes avec une troisième de telle façon que la somme des angles intérieurs d’un côté est inférieure à deux angles droits, alors ces deux lignes sont forcément sécantes de ce côté (autrement dit : par un point extérieur à une droite donnée, ne passe qu’une unique droite qui lui est parallèle).
Cela produit des raisonnements et des conclusions assez perturbantes. Voir certains paradoxes ici.
| Géométrie Euclidienne | Géométrie non Euclidienne |
|
|
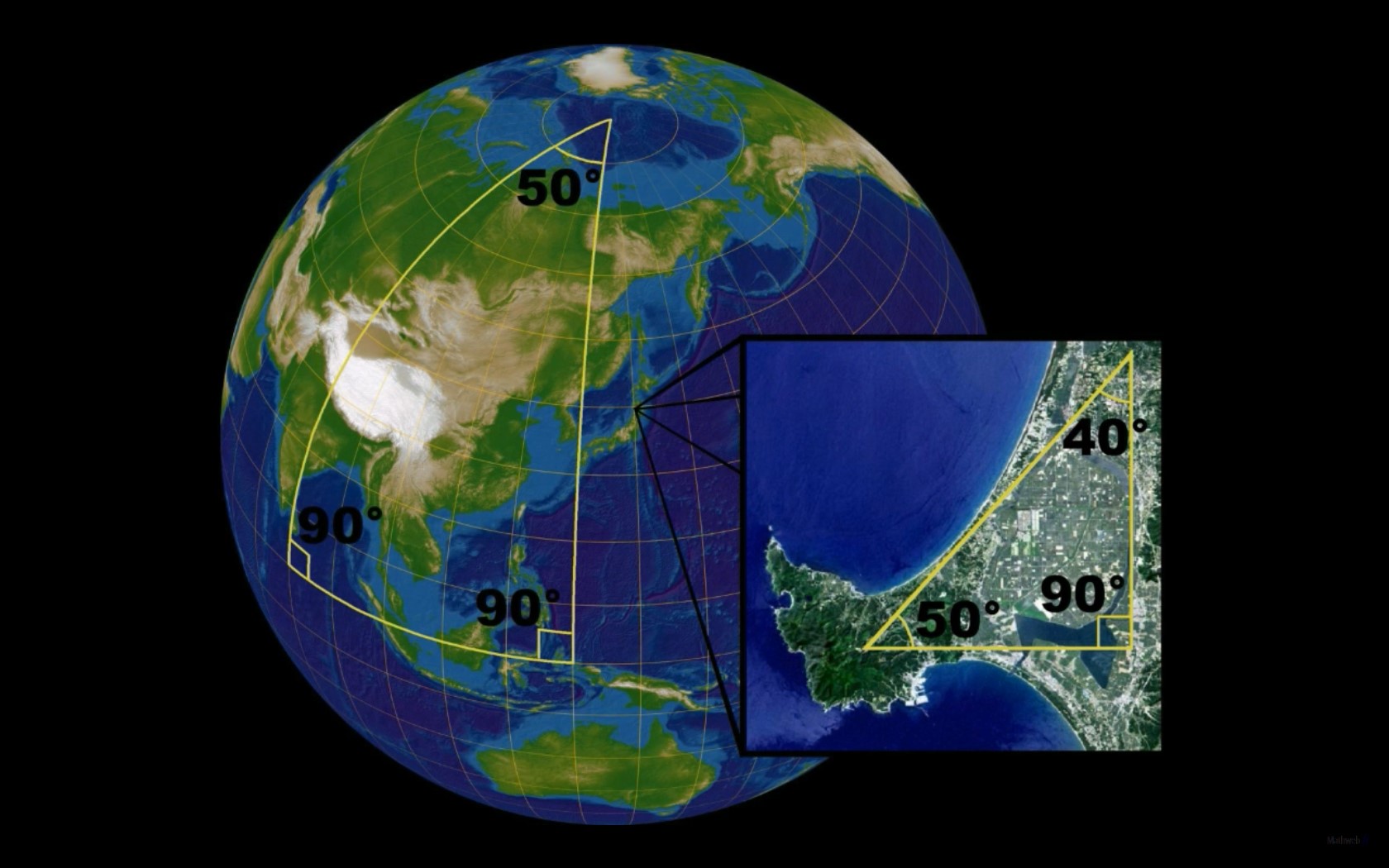 2 droites parallèles peuvent se croiser. Par exemple les longitudes de la terre. |
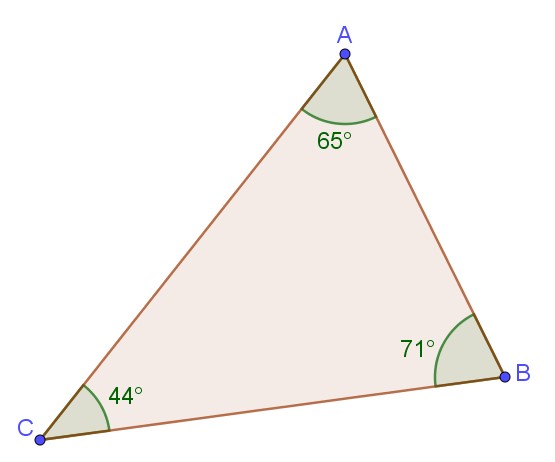 Dans un triangle la somme des 3 angles fait 180°. |
Prenez un ballon de baudruche ou de foot, et tracer un triangle à sa surface : la somme de ses 3 angles sera supérieure à 180°. Et si la courbure du volume est négative, alors cette somme sera inférieure à 180°. |
Il existe deux grandes géométries non Euclidienne :
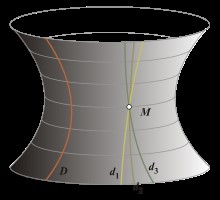
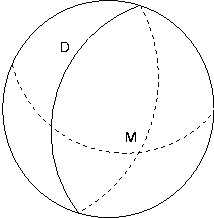
| 1°/ La Géométrie hyperbolique : | 2°/ La Géométrie elliptique : |
|
|
Le modèle est très simple : |
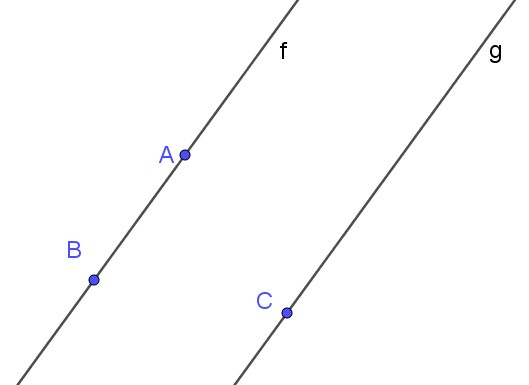
Selon le référentiel dans lequel ou se trouve, les droites ne se comportent pas de la même façon :
 |
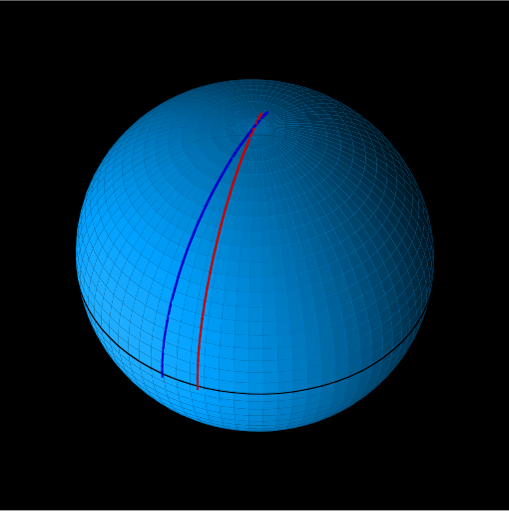 |
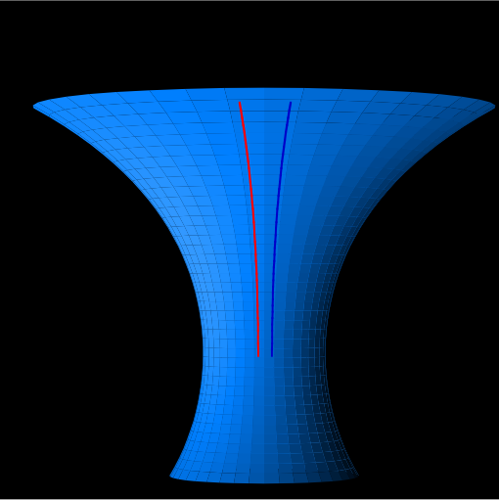 |
| Sur un plan 2 droites parallèles ne se croisent pas. | Sur une sphère 2 droites parallèles se rejoignent aux pôles. | Sur une hyperbole 2 droites parallèles s’éloignent. |
III°/ La cartographie :
1°/ Les cartes de la terre au fil des âges :
Voici quelques cartes caractéristiques. Cliquez sur certaines carte pour l’agrandir.
|
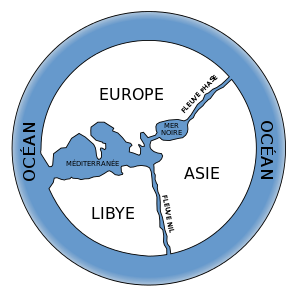
Le philosophe grec Anaximandre (mort vers -546) aurait été le premier à proposer une carte du monde. Elle ne nous est pas parvenue, mais peut être reconstituée grâce à des descriptions ultérieures. Anaximandre considère le monde comme circulaire, avec la mer Égée pour centre. Il est divisé en trois continents : l’Europe, la Libye (l’Afrique) et l’Asie. L’Europe est séparée de la Libye par la mer Méditerranée et de l’Asie par le Pont-Euxin et le Phase. Le Nil sépare l’Asie de la Libye. Les continents sont entourés par un océan extérieur. |
Hécatée de Milet : Hécatée de Milet (mort vers -480) se serait inspiré d’Anaximandre pour proposer sa propre carte du monde, qui accompagne sa Périégèse (uniquement connue à travers des citations).
|
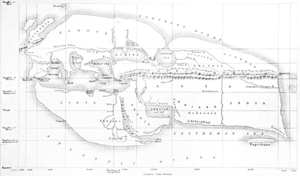
Ératosthène : La carte d’Ératosthène (mort vers -194) incorpore des découvertes faites lors des conquêtes d’Alexandre le Grand et ses successeurs. Cliquez sur la carte pour l’agrandir.
|
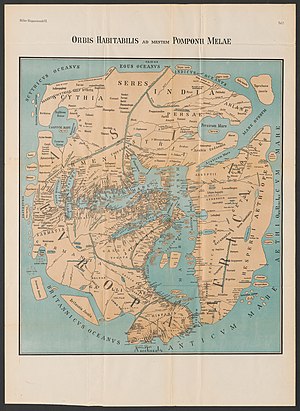
Pomponius Mela : Pomponius Mela est le plus ancien géographe romain connu. Cliquez sur la carte pour l’agrandir. |
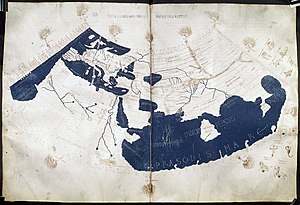
Ptolémée : Basée sur la description du monde contenue dans l’ouvrage de Ptolémée Geographia, écrit vers 150 de notre ère. Cliquez sur la carte pour l’agrandir. |
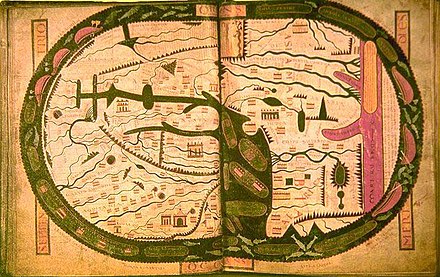
Mappa Mundi de Beatus (vers 1050) : Beatus de Liébana (v. 730 – 798) était moine au monastère Saint-Martin de Liébana, en Espagne. Dans cette mappemonde, on trouve la carte en T, qui sera progressivement abandonnée à partir du XIIe siècle. |
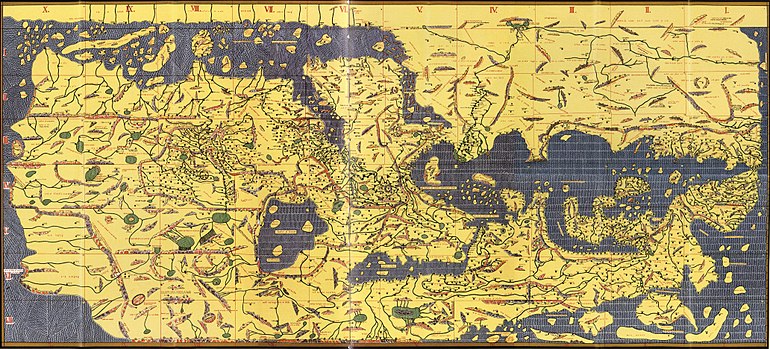
Carte d’Al Idrissi (vers 1154) : Le géographe arabe Al Idrissi a inclus, avec les informations héritées de l’Antiquité classique, les connaissances sur l’Afrique et l’océan Indien que les marchands arabes et les explorateurs avaient glanées depuis. Il réalisa ainsi les cartes les plus précises et les plus complètes de son temps. Dans cette carte, le nord est en bas, et le sud en haut. Cliquez sur la carte pour l’agrandir. |
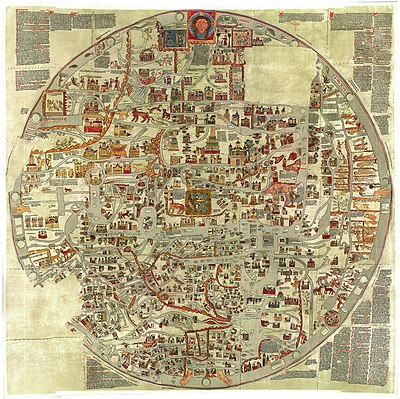
Mappa Mundi d’Ebstorf (vers 1300) : Elle mesure 3,6 sur 3 mètres, et contient plus de 2300 données sous forme de textes ou d’images, ce qui en fait la plus grande et la plus complexe des cartes médiévales connues. Elle était composée de 30 feuilles de parchemin cousues ensemble. Cliquez sur la carte pour l’agrandir. |

Mappa Mundi d’Hereford (vers 1300) : C’est une carte T dans l’O, présentant une manière de perfectionnement du genre. Elle est signée par un certain « Richard de Haldingham ou de Lafford ». |
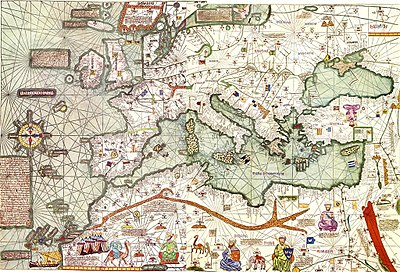
Atlas catalan (1375) : attribuée à Abraham Cresques, cartographe de l’école majorquine. L’« atlas » se compose de six feuilles de vélin. Elle s’appuie sur les récits de Marco Polo pour sa partie orientale. Cliquez sur la carte pour l’agrandir. |

La carte Kangnido (1402) : Réalisée en Corée en 1402, à partir de sources chinoises, par Gim Sa-hyeong Li Mu et Li Hoi . Elle décrit la totalité du monde connu à l’époque par les Coréens : la Corée et le Japon à l’est; la Chine surdimensionnée au centre. |

Planisphère de Virga (1411-1415) : Carte réalisée par Albertin de Virga. Ce planisphère est circulaire.
|
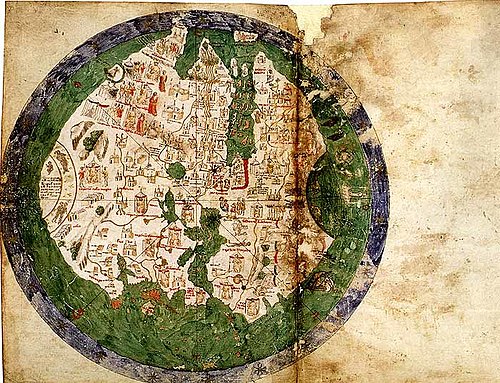
Atlas d’Andrea Bianco (1436) : Andrea Bianco fut un collaborateur d’un autre cartographe vénitien Fra Mauro.
|

Planisphère de Fra Mauro (1459) : Carte a été dessiné par Fra Mauro et son assistant Andrea Bianco. La carte représente de manière étonnante l’océan Indien et surtout la partie australe de l’Afrique, à une époque où aucun Européen ne s’y était encore aventuré. Il est plausible que ces renseignements soient parvenus de Chine en Italie par l’intermédiaire de marchands. Cliquez sur la carte pour l’agrandir. |
Seule carte attribuée à Christophe Colomb. Cette carte nous fournit un état des lieux des connaissances géographiques juste avant la découverte des Amériques. Cliquez sur la carte pour l’agrandir. |
|
Donnée par Alberto Cantino à S. duc Hercule ») appelée le planisphère de Cantino, datée de 1502. Cliquez sur la carte pour l’agrandir.
|
Il est imprimé sur douze planches, le tout faisant 2,32 mètres de long. Le nom « America » se trouve en bas à gauche ; la projection du planisphère est cordiforme (en forme de cœur) ; au-dessus, de part et d’autre d’une mappemonde (représentation des deux hémisphères) se trouvent les portraits de Ptolémée et de Vespucci. Cliquez sur la carte pour l’agrandir. |
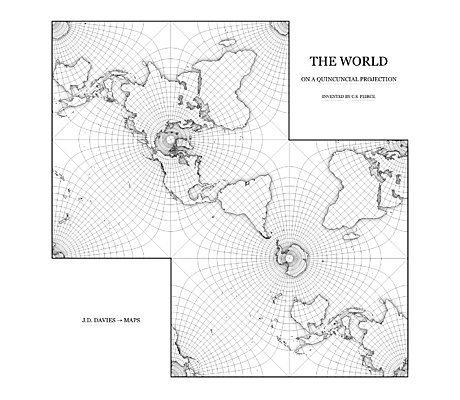
Les parallèles et méridiens dessinent un quadrillage orthogonal. Cette projection cartographique préserve les angles (essentiels pour la navigation) en déformant les surfaces et les distances au fur-et-à-mesure qu’on s’éloigne de l’équateur. L’impression sur papier permit une large diffusion de ces cartes, d’où la monochromie. Cliquez sur la carte pour l’agrandir. |
|
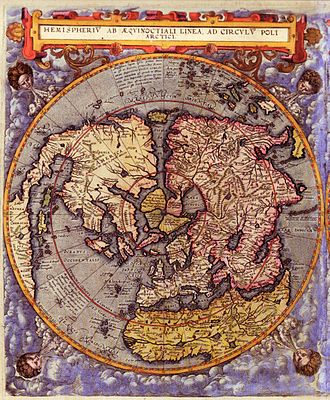
Imprimée à Anvers en 1593, elle représente l’hémisphère nord du globe terrestre. Cliquez sur la carte pour l’agrandir. |
L’âge d’or des cartes marines : XVe – XVIe siècle
|
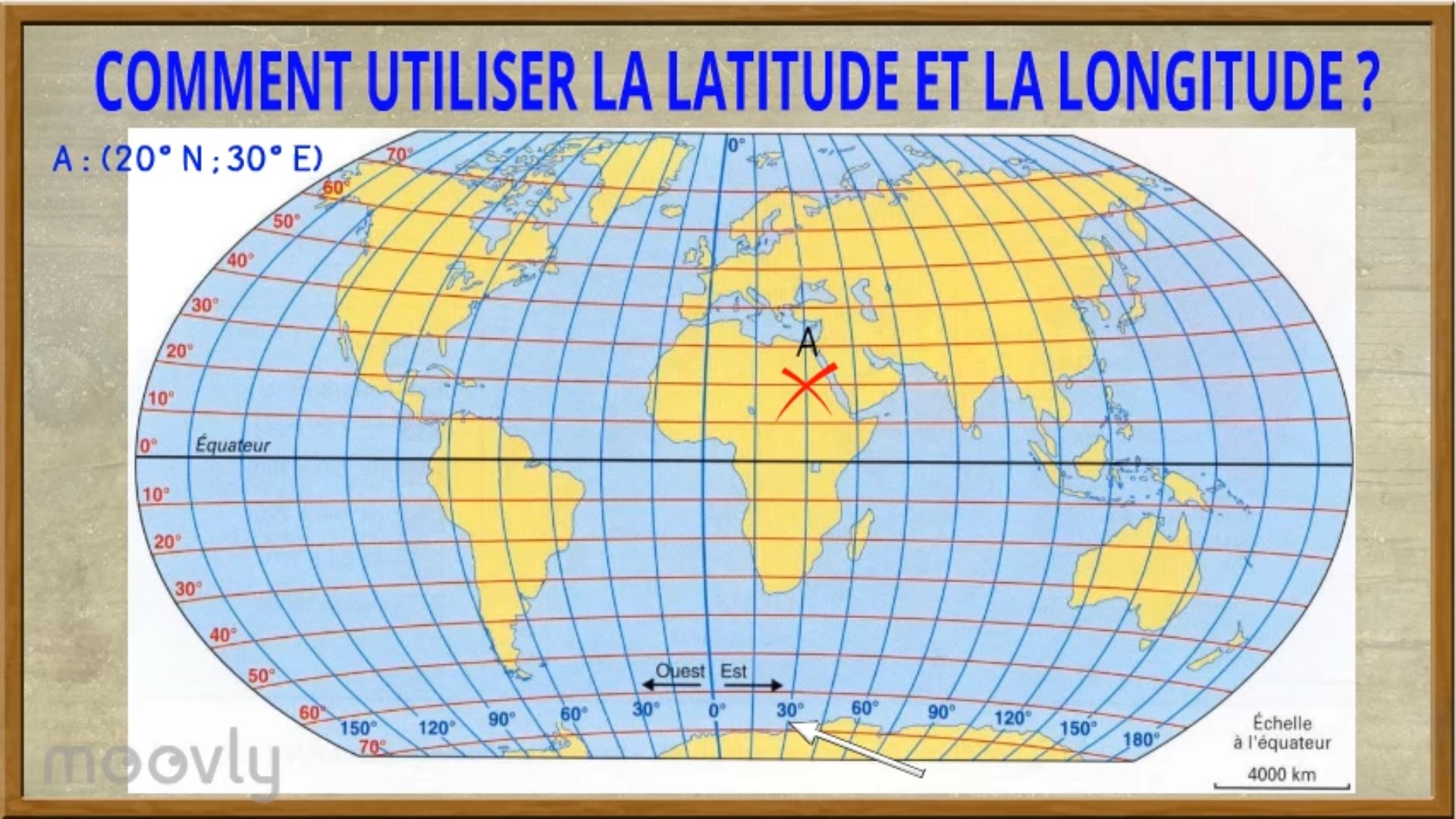 |
Un méridien est une ligne verticale imaginaire, qui relie les deux pôles. La longitude d’un méridien représente la valeur angulaire (de 0° à 180°) d’un point du globe par rapport au méridien de Greenwich, qui est la longitude de référence sur Terre. Un parallèle est une ligne horizontale imaginaire, qui est parallèle à l’équateur. La latitude d’un parallèle représente la valeur angulaire (de 0° à 90°) d’un point du globe par rapport à l’équateur. La croix rouge ci-contre a comme coordonnées : 20° Nord et 30° Est. Cliquer sur la carte pour accéder à un GPS. |
|
|
|
Comment mesurer sa latitude sur terre ?
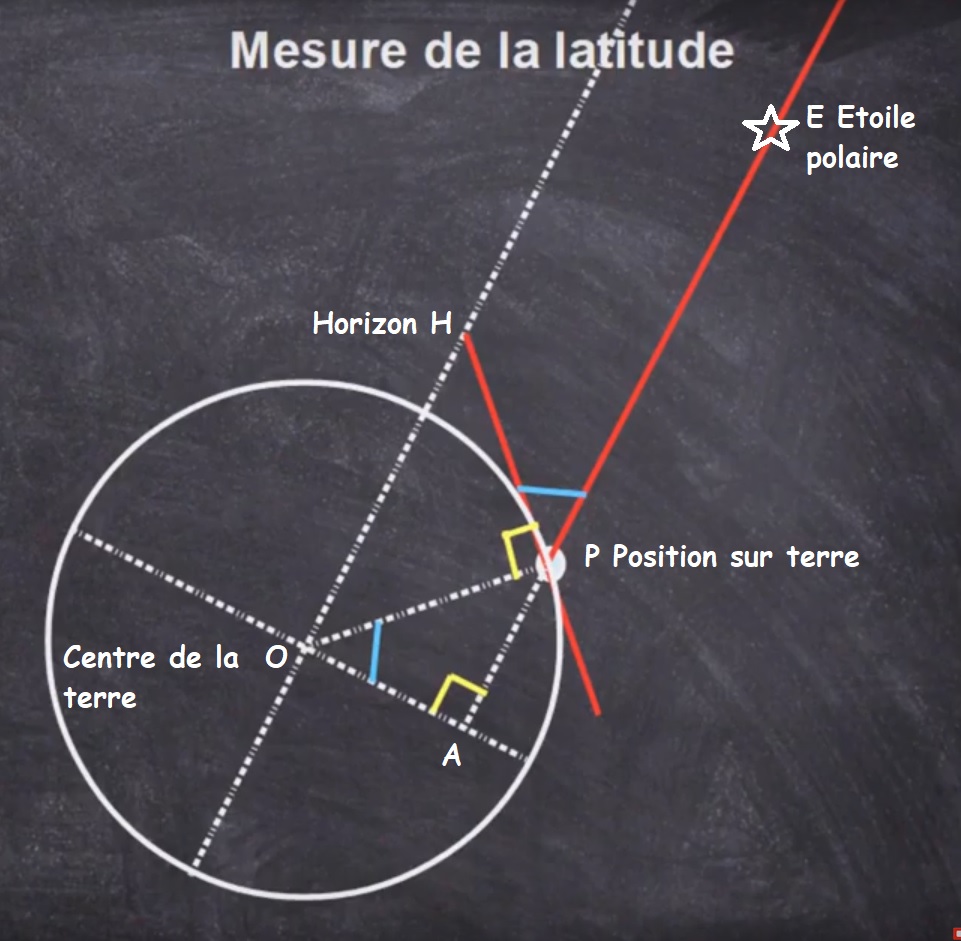 |
De sa position P il faut viser l’horizon H avec un sextant ainsi que l’étoile polaire E. Cette étoile étant très loin, on peut considérer que (EP) // (HO). Ainsi : \widehat{EPH} = \widehat{POA} qui nous donne notre latitude. |
3°/ Représentations des cartes modernes :
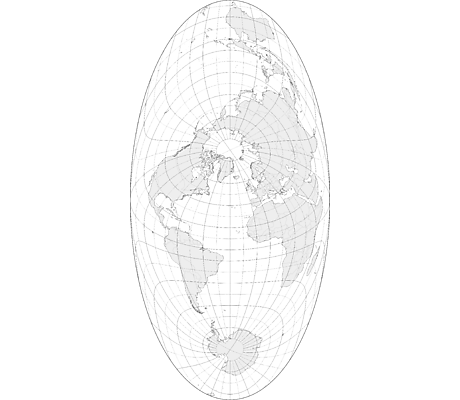
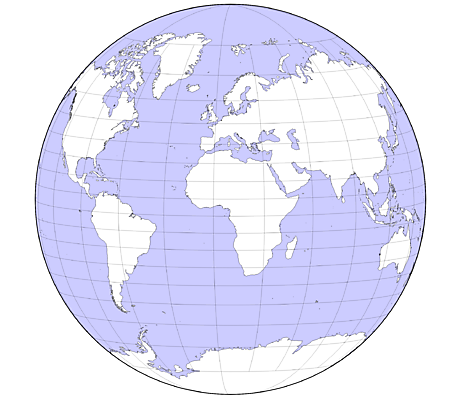
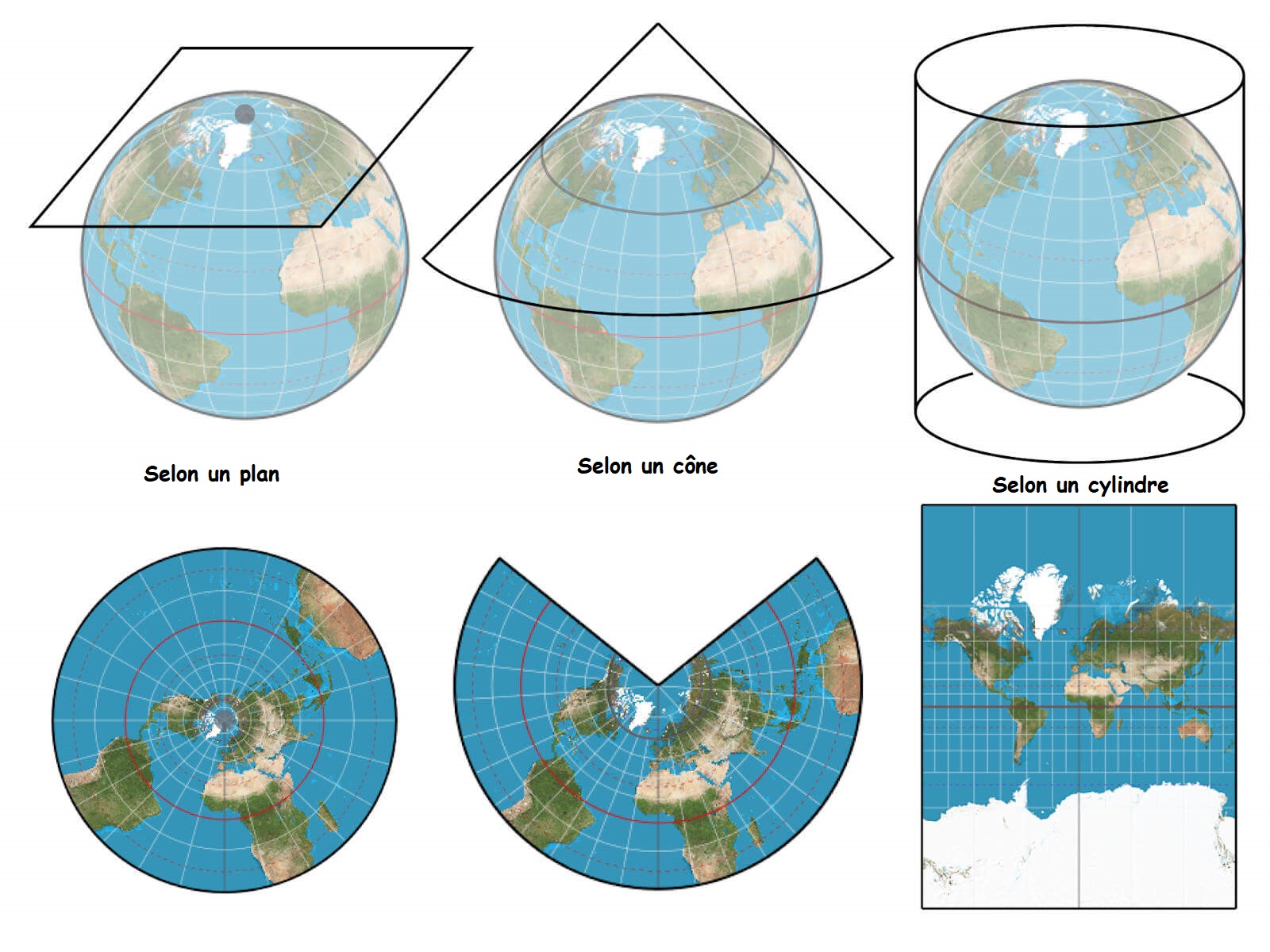
Pour représenter la terre, qui est une boule en 3D, sur une surface plane en 2D, il faut effectuer une projection. Cependant, quand on veut représenter un objet sphérique tridimensionnel sur une surface plane en 2D, on ne peut pas éviter les déformations de certaines régions, qui sont étirées ou aplaties.
|
|
|
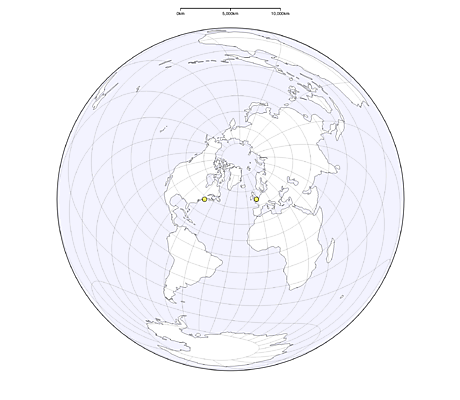
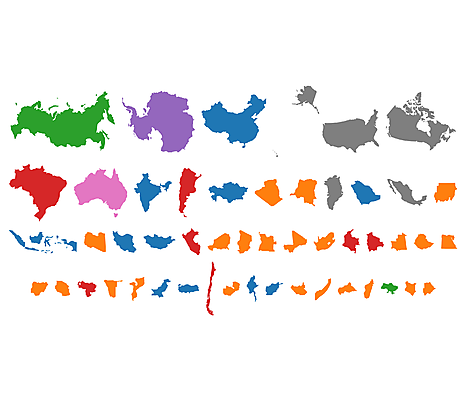
En 1859, Nicolas Auguste Tissot, un géographe français, inventa une méthode qui permet de visualiser les déformations des cartes suivant leur modèle. Avec l’outil ci-dessous, déplacez la souris sur la carte. Plus on s’écarte de l’équateur et plus le cercle s’étire ainsi que les pays.
Encore plus fort, avec ce site vous choisissez votre pays et vous pouvez alors comparer sa taille avec le reste du monde.
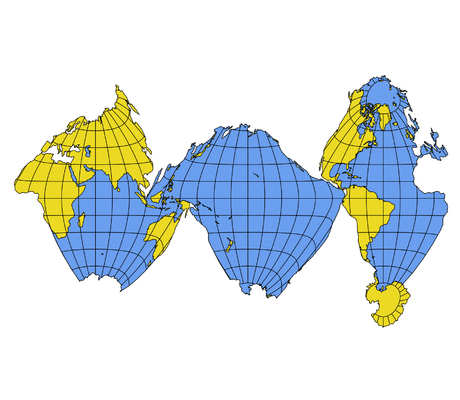
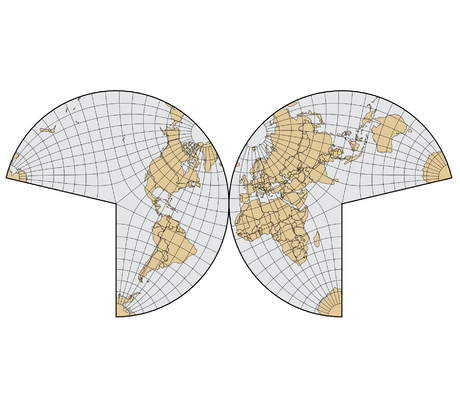
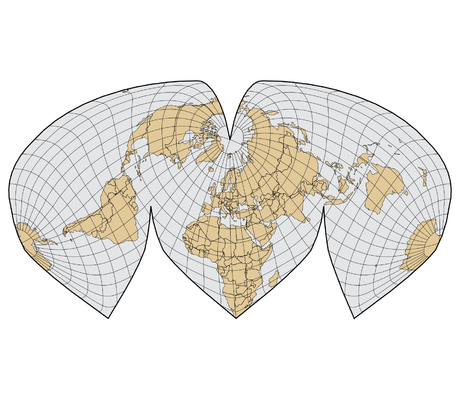
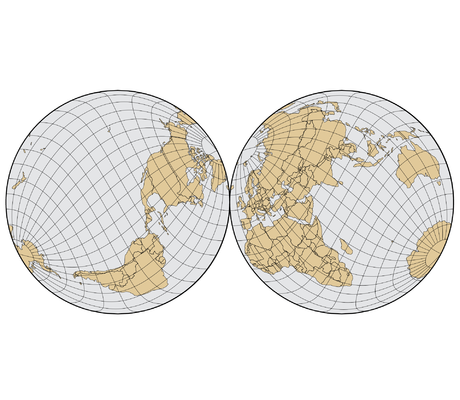
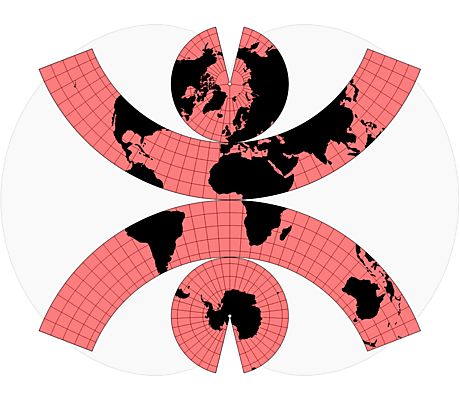
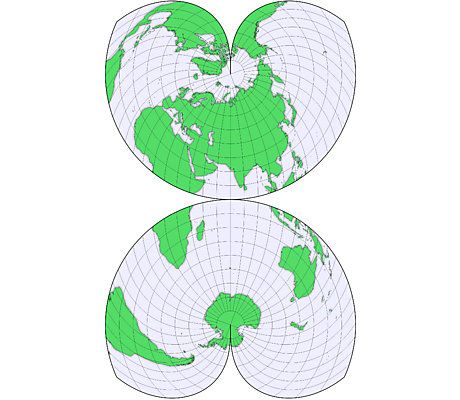
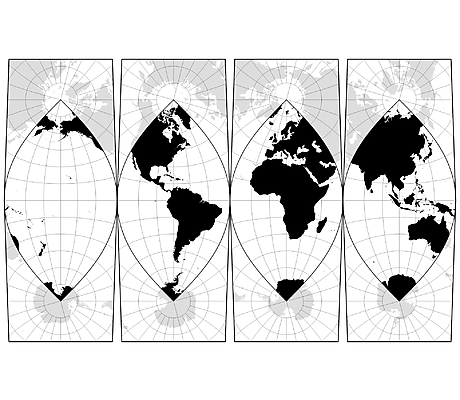
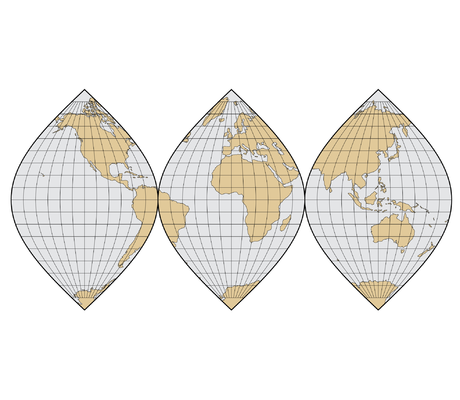
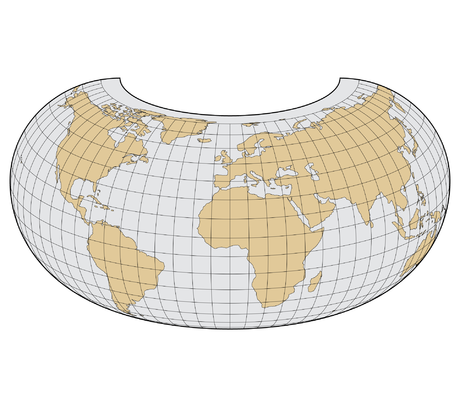
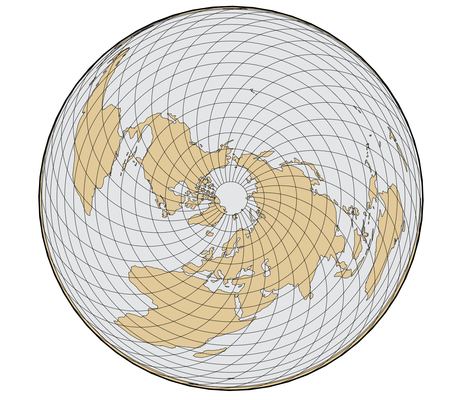
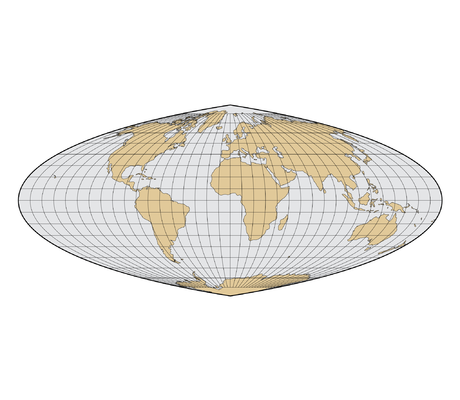
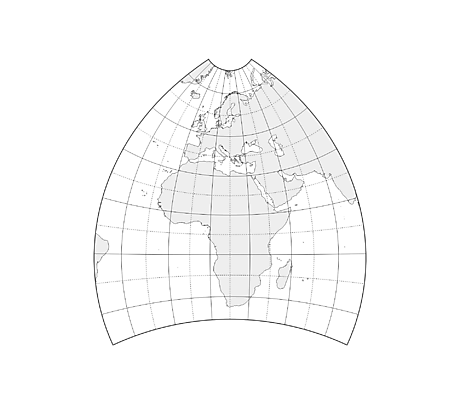
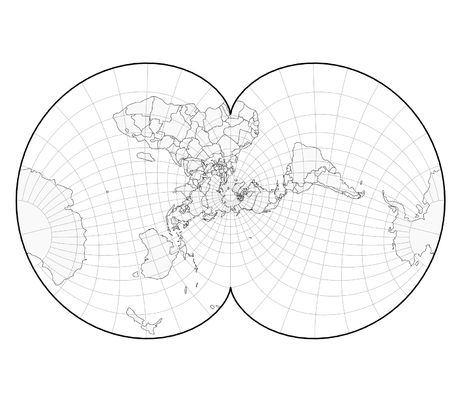
Voici différentes projections, qui ont toutes des avantages et des inconvénients :
 |
|
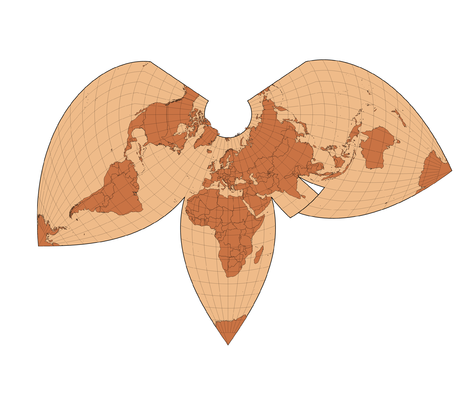
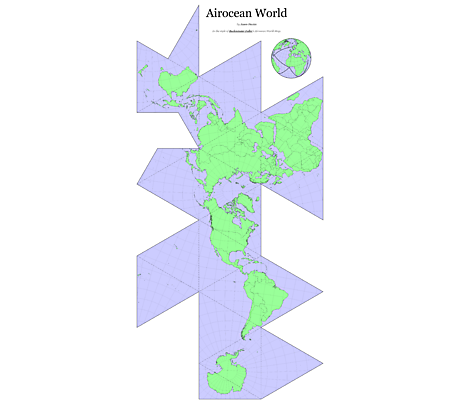
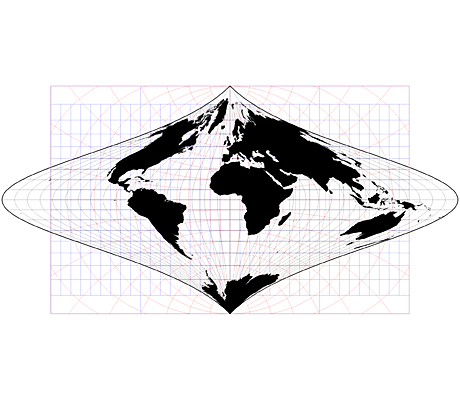
La carte la plus réaliste date de 1999 et elle est l’œuvre de Hajime Narukawa, un architecte japonais. Il a remporté plusieurs prix et sa carte est en passe d’être considérée comme la plus fidèle. Ce n’est évidemment pas parfait mais c’est ce qui s’en approche le plus pour le moment. En fait, il a repris la projection de Fuller (de 1946).
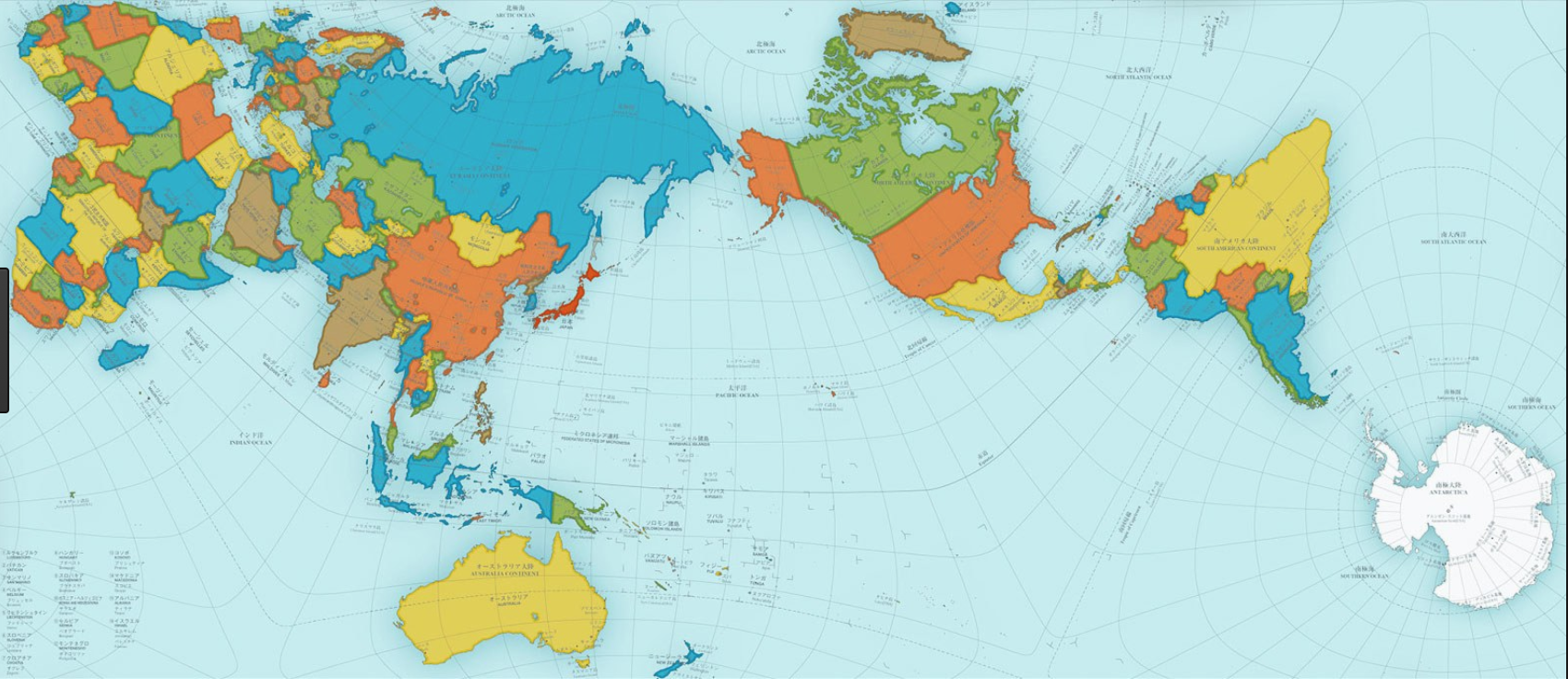 Carte de Hajime Narukawa. Carte de Hajime Narukawa. |
|
Certaines sont très originales :
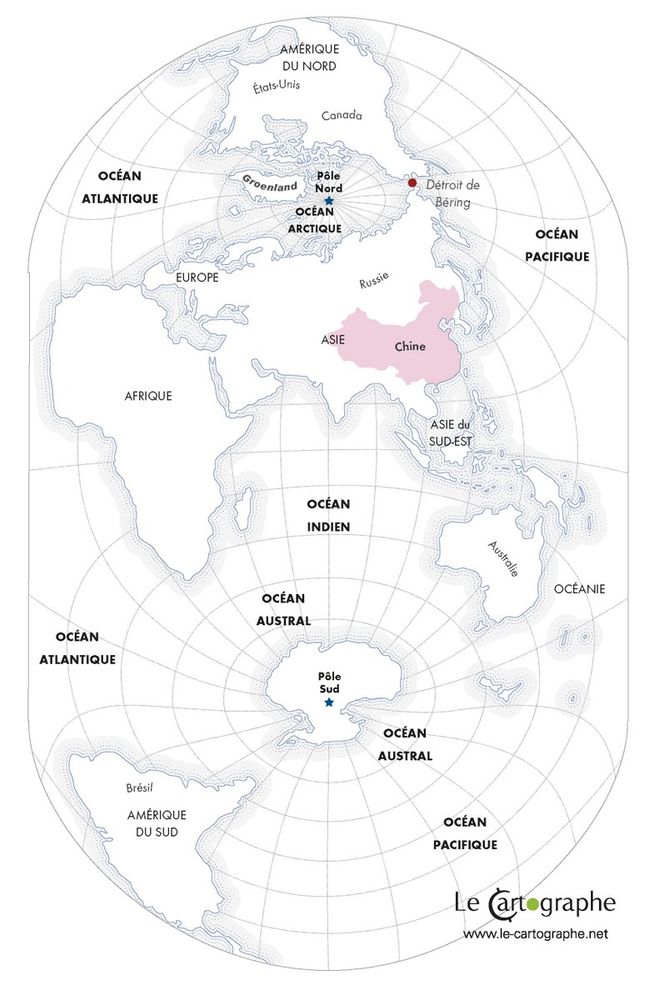 |
Une carte de Hao Xiaoguang, centrée sur la chine. Remarquez la place des USA et surtout sa taille. |
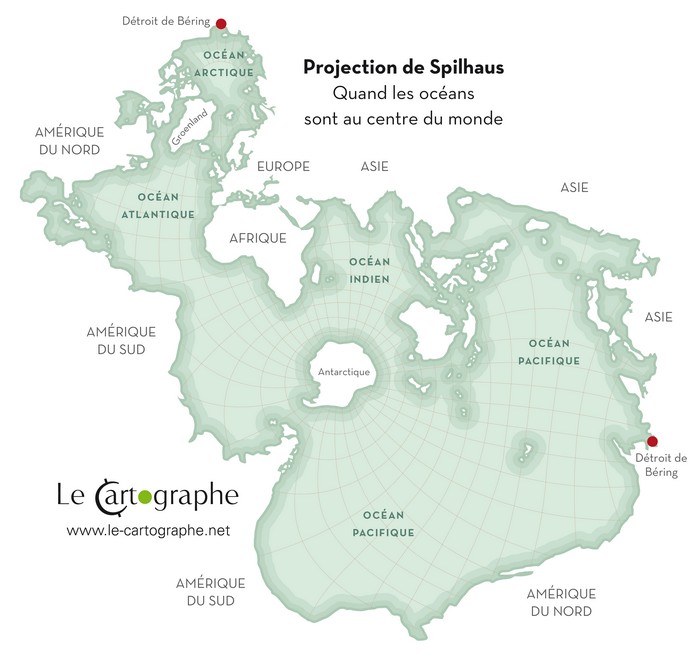 |
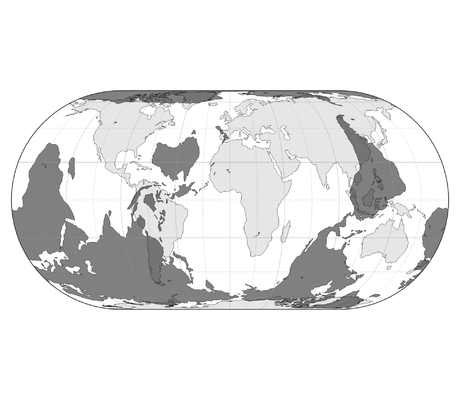
La carte de Spilhaus : C’est la carte de la terre vue par un poisson où les océans sont mis en avant. En 1942, l’océanographe et géophysicien Athelstan Frederick Spilhaus d’origine sud-africaine, réalise une carte fascinante. Les régions marines sont représentées au centre du monde. Une immense mer intérieure (un peu plus de 70% de la surface de la Terre) apparait sous nos yeux. Rappelons tout de même que l’Océan mondial génère plus de 60% des services écosystémiques qui nous permettent de vivre, à commencer par la production de la majeure partie de l’oxygène que nous respirons. Cette carte est ainsi toute symbolique de l’importance des mers. Afin de réaliser celle-ci l’auteur utilise les principes des deux projections suivantes. La projection de Ernst Hammer et celle d’August Heinrich Petermann (co-auteur avec Hermann Berghaus et Carl Vogel de l’Atlas Stieler). Le résultat est une projection interrompue dans laquelle les océans forment une unité. C’est à la fois génial et totalement déroutant. La déformation est telle que le continent américain et asiatique sont complétement écartelés. L’Europe, l’Afrique et l’Asie du Sud-Est conservent en revanche une forme cohérente. Cette projection est rarement utilisée et c’est bien dommage ! |
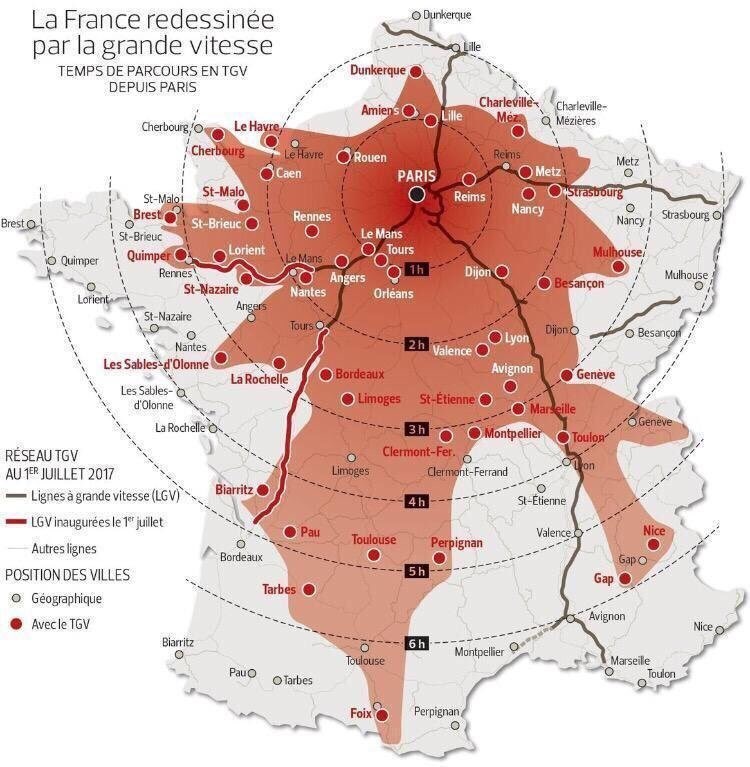 |
La France redessiné par le TGV : Regardons la France autrement. A quoi ressemblerait-elle si on la dessinait non plus en respectant les distances kilométriques, mais en tenant compte du temps qu’il faut en TGV pour relier Paris aux métropoles régionales? Le résultat, vous l’avez sous les yeux. Le nord du pays se trouve ramassé, tandis que le sud, plus « lent », s’étale sur une large surface. C’est le principe des cartes, dites « isochrone ». |
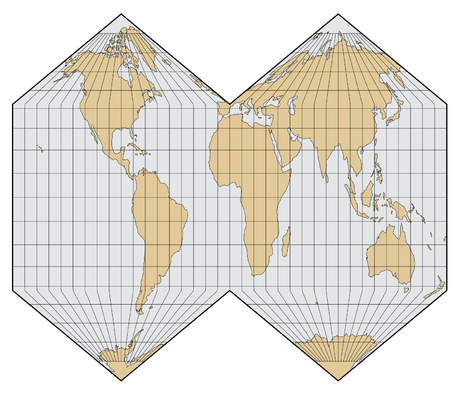
– Les projections interrompues : Il faut bien décider où découper le globe pour fabriquer la carte plane. Ces interruptions se produisent souvent dans des zones de moindre intérêt, par ex. océans pour une carte terrestre. Plus classiquement le long d’un méridien.
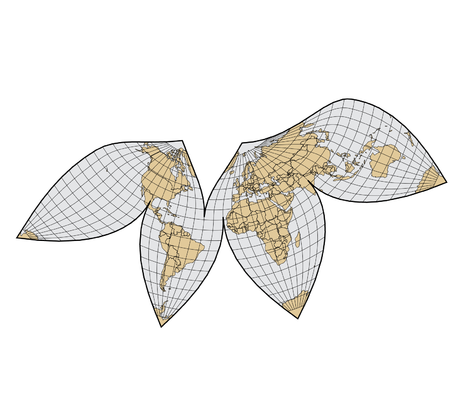
– Cartes papillons : La manière la plus courante de disposer un octaèdre de huitièmes triangles équilatéraux est connue sous le nom de «carte papillon».
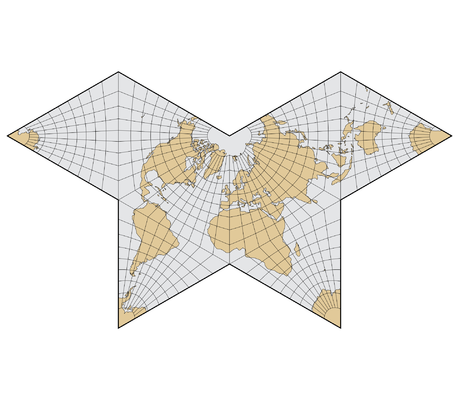 Gnomonic Butterfly Map Gnomonic Butterfly Map |
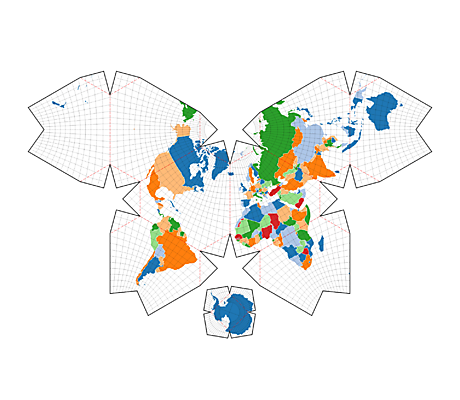 Waterman Butterfly Map Waterman Butterfly Map |
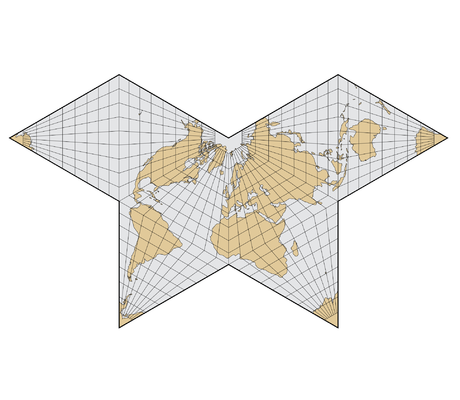 Collignon Butterfly Map Collignon Butterfly Map |
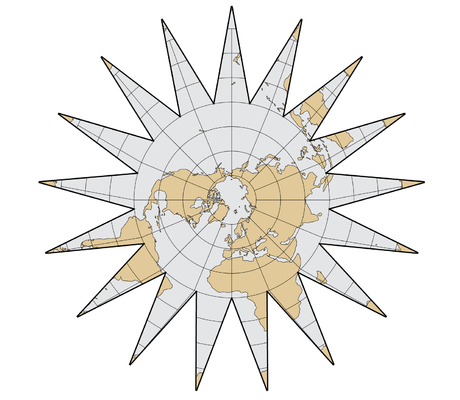
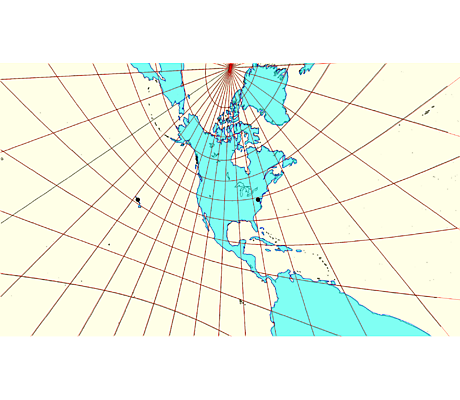
– Projections rétroazimutales : Une projection rétroazimutale montre le véritable azimut du centre à partir de tous les autres points. Les cartes sont interactives.
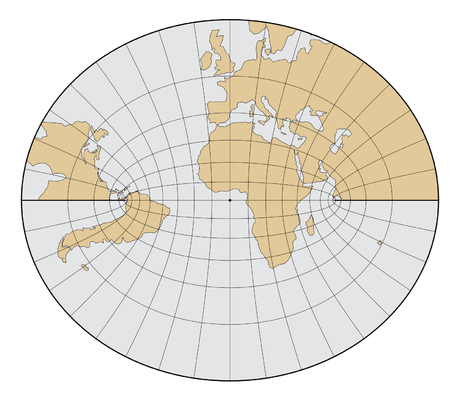 Littrow Projection Littrow Projection |
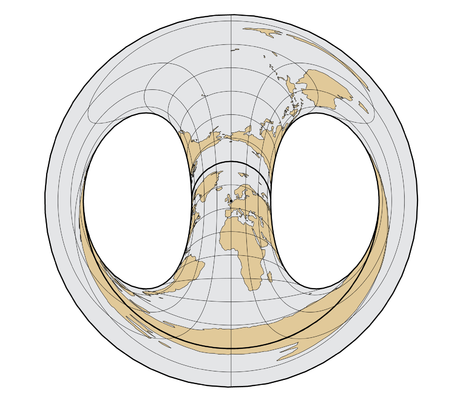 Hammer Retroazimuthal Projection Hammer Retroazimuthal Projection |
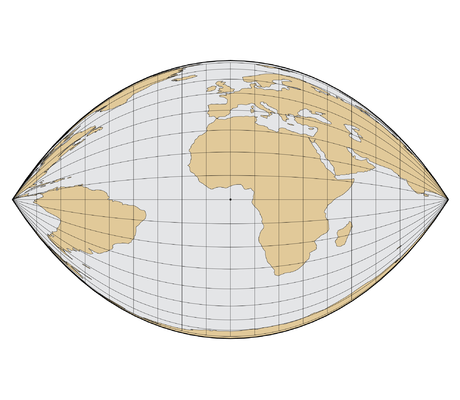 Craig Retroazimuthal Projection Craig Retroazimuthal Projection |
– Projections diverses : certaines cartes sont interactives.
Références : https://www.jasondavies.com/maps/
IV°/ L’Everest est-il le plus haut sommet ?
La question est originale, car tout le monde sait que L’Everest culmine à 8 849 m et que c’est le plus haut sommet sur la terre.
Oui, mais en prenant comme référence le niveau de la mer, ce qui est tout à fait commun. Cependant, en prenant le centre de la terre comme référentiel, L’Everest est détrôné par le Chimborazo qui est un volcan d’Équateur. En effet la Terre n’est pas tout à fait ronde. Elle est légèrement aplatie aux pôles et gonflée au niveau de l’équateur.
| Par rapport au niveau de la mer | Par rapport au centre de la terre | |
| Everest | 8 849 m | 6 382,6 m |
| Chimborazo | 6 236 m | 6 384,4 m |
Le fleuve Mississippi, aux États-Unis, possède une étrange propriété. Sa source, située dans le Parc Itasca du Minnesota, est plus proche de 5 km du centre de notre planète que son embouchure dans le golfe du Mexique. Le fleuve américain semble couler vers le haut ! Mais ce n’est qu’une illusion et si on se réfère au niveau de la mer, les choses reviennent dans l’ordre : le Mississippi prend sa source à 450 mètres d’altitude pour la terminer à 0 mètre. L’eau du fleuve coule bien vers le bas, mais en se dirigeant vers le sud, elle se rapproche de l’équateur gonflé et s’éloigne donc du centre.

 Anaximandre :
Anaximandre :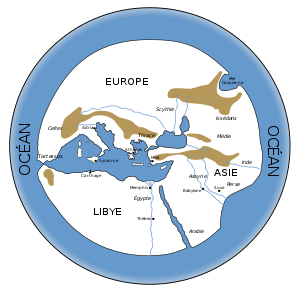

.jpg)


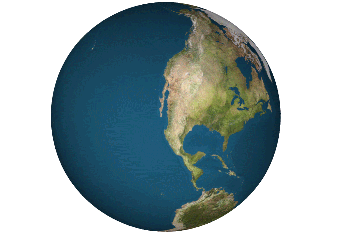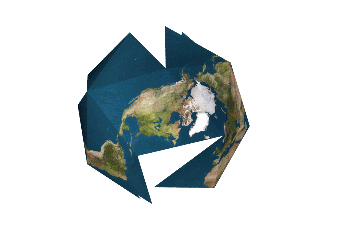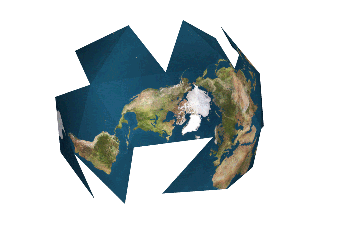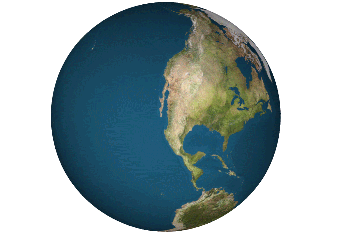 Projection de Fuller.
Projection de Fuller.