Ceux qui ont fait un peu de solfège connaissent la suite de notes, dans laquelle chaque note est à la quinte de la suivante : SI, MI, LA, RE, SOL, DO, FA (les Anglo-Saxons utilisent plutôt les lettres A, B, C, D, E, F et G).
 |
C’est au XI siècle que le moine Guido d’Arezzo (991-1050) a l’idée de donner un nom aux notes. Il utilise la première syllabe des hémistiches (la moitié d’un vers) des 6 vers de l’hymne de Saint Jean-Batiste, attribué à Paul Diacre (730-799).
On obtient 6 notes : Ut, Ré, Mi, Fa, Sol, La. Au XVI siècle, Anselme de Flandres rajoutera la 7ième note Si. La dernière modification concernera la note Ut, qui étant difficile à prononcer, sera transformé en Do. On obtient alors nos 7 notes : Do, Ré, Mi, Fa, Sol, La, Si. |
Mais d’où vient cette suite ? Et que vient faire le nombre 5 (quinte) dans cette affaire ? Et pourquoi y a-t-il 7 notes principales si curieusement liées entre elles ?
On perçoit une petite lueur de compréhension en plaçant les notes sur les bords d’une horloge ou chaque heures représentent un demi-ton. Ainsi on se rend compte que chaque note est séparée de sa voisine pas un ton, sauf MI et FA d’une part ainsi que SI et DO d’autre part, qui sont séparées par un 1/2 ton. De plus on verra se tracer 7 cordes joignant les notes de cinq en cinq.
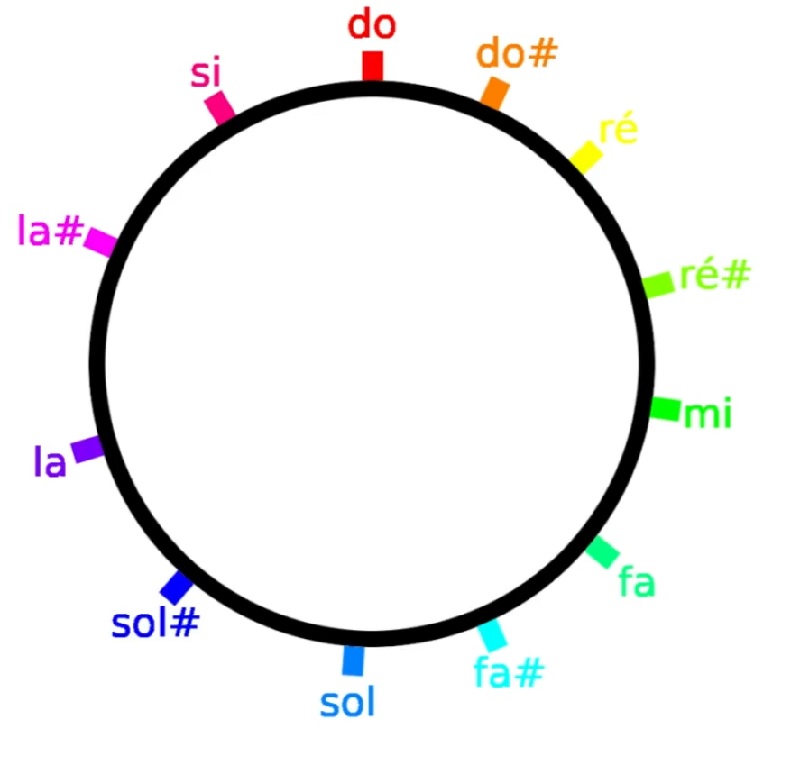 |
 |
| On voit que les notes ne sont pas uniformément réparties dans cette gamme dite Pythagoricienne. Mathématiquement parfaite. | Simon Stevin (Pays Bas 1548-1620) harmonise les notes. Gamme dite de tempérament égal. Auditivement parfaite. |
En fait les rapports entre les nombres et la musique étaient bien connus des chinois, vers 20 siècles avant J-C et du monde grec, 6 siècles avant J-C. En effet, on attribue à Pythagore la découverte de l’explication physique de ces rapports.
Tout vient des impressions que produisent à nos oreilles les cordes que l’on fait vibrer. Ainsi si l’on pince trois cordes de métal (comme une corde de guitare) de longueur L, 2L et 3L, et qu’on les fait vibrer, les vibrations transmises par l’air à notre oreille donnent à un musicien l’impression d’entendre un FA (par exemple) pour la première corde, un son plus grave mais qui représentent le même FA de l’octave en dessous pour la deuxième, est un DO pour la troisième. Ce qui est magique, c’est que ces trois notes semblent être en accord, et le musicien perçoit des notes qui vont bien ensemble.
Évidemment on peut dire la même chose si, au lieu de multiplier les longueurs des cordes par 2 ou 3, on les divisait par 2 ou 3 :
– Les cordes de longueurs respectives 1, 1/2, 1/4, 1/8, …, 2, 4, 8, 16, … émettent des sons qui semblent être la même note (à des octaves différents).
– Les cordes de longueurs 1, 3, 9, … mais aussi 1/3, 3/2, 2/3, 3/4, 4/3, … émettent des sons qui vont bien ensemble.
Tout se passe donc entre les puissances de 2 et de 3, ainsi que leurs rapports. L’idéal serait de n’émettre que des sons qui vont bien ensemble 2 par 2, c’est à dire de manipuler les cordes de longueurs : 1, 3/2, 32 / 22, 33 / 23 ou des sons doubles, quadruples, 23, 24, …sont les mêmes ( à un octave prés) : 1, 3, 32, 33, 34, …
L’ennui, c’est que l’on engendre ainsi une infinité de notes émises par les cordes dont les longueurs sont des puissances de 3, à des divisions par 2 prés.
Évidemment s’il arrivait qu’une certaine puissance de 3 soit aussi une puissance de 2, ont pourrait arrêter la suite et on aurait une suite de notes allant bien ensemble. Malheureusement l’arithmétique est impitoyable : aucune puissance de 3 ne vaut exactement une puissance de 2 ! Mais, heureusement, notre oreille a ses limites de perceptions et il y a des puissances de 3 qui ne sont pas loin de certaines puissances de 2.
 |
Si vous avez une guitare, vous pouvez vérifier que les longueurs des cordes pincées entre les barres du manche et leur attache commune sont bien exactement les longueurs calculées à partir des puissances de 2 et de 3, l’unité mesurant entre 30 et 35 cm selon les guitares.
Cependant, faire de la musique s’est un peu plus compliqué que de faire des mathématiques, et seule la sensibilité du musicien peu rendre la musique si belle.
Google Chrome propose de petits jeux pour pour joueur avec la musique :
