Il est impossible aux habitants de ce monde de se faire la moindre idée du néant, de l’infini et de Dieu, disait Jean d’Ormesson.
La notion d’infini est assez compliquée à appréhender. Que peut-on compter qui soit infini, y-a-t’il des infinis plus grand que d’autres ….
I°/ Paradoxe de Galilée :
II°/ Les symboles :
III°/ Les très grands nombres :
Voici une superbe vidéo de ARTE :
Et voilà une très riche vidéo de Science Etonnante :
Et enfin El JJ qui tente de nous donner le plus grand nombre imaginable :
I°/ Paradoxe de Galilée :
Est-ce que la quantité des nombres entiers est plus grande que celle des nombres pairs ?
Il est évident que les nombres entiers sont soit pairs soit impairs, et on en déduit que les nombres entiers sont deux fois plus nombreux que les nombres pairs. Et pourtant, à chaque nombre on peut associer son double, donc on peut conclure que leur quantités A et C sont égales !!!
Conclusion : à l’infini, la notion de « plus grand, plus petit ou égal » n’est pas applicable. La partie d’un ensemble peut être aussi grande que l’ensemble qui le contient.
Un mathématicien Allemand Georg Cantor, définit la notion de bijection des ensembles. Il y a bijection entre deux ensembles quand on peut associer chaque élément d’un ensemble à chaque élément de l’autre. A cet condition, les cardinaux, cad leur quantités, des deux ensembles sont égaux.
 |
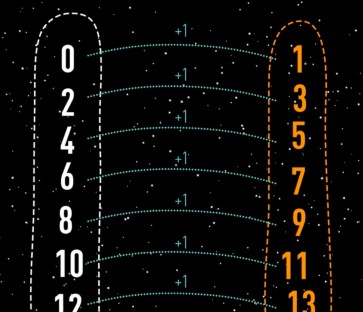Si on compare l’ensemble des nombres pairs avec celui des nombres impairs, il y a bijection entre les deux ensembles. Leurs cardinaux sont bien égaux et c’est logique. |
 |
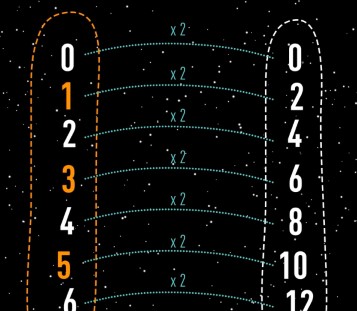Si on compare l’ensemble des nombres entiers avec celui des nombres pairs, il y a bijection entre les deux ensembles puisqu’il suffit de multiplier par 2 chaque entiers pour trouver un nombre pairs. Leurs cardinaux sont bien égaux et ce qui est moins logique. |
Comparons à présent la quantité de nombre réel qu’il y a entre le nombre entier 0 et 1.
 |
Chacun de ces nombres s’écrira avec un zéro et une virgule suivie d’une infinité de décimale ou pas. Disposons-les dans un tableau infini, dont le nombre de ligne représente l’ensemble infini des nombres entiers, et relevons la première décimale du premier nombre, puis la deuxième décimale du deuxième nombre etc., et formons un nombre. Ici 0,430 417 … . |
 |
Ajoutons 1 à chaque chiffre du nombre ainsi créé. Ce nouveau nombre sera obligatoirement différent de n’importe quel nombre précédent, car il aura au moins une décimale de différence. Et on peut ajouter une infinité de nombre et ainsi créer une infinité de nombre différent. Il n’y a pas bijection entre l’ensemble des nombres réels comprit entre 0 et 1. Autrement dit, l’infinité de nombres réels comprit entre 0 et 1 est plus grand que l’infinité des nombres entiers eux-même. |
Il y a plusieurs infinis :
– L’infini dénombrable (que l’on peut compter ou numéroter à l’aide des entiers naturels) qui n’a pas de bornes. Il est noté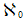 
( aleph, qui est la 1ére lettre de l’alphabet Hébreu ).
Par exemple, les ensembles des nombres entiers, relatifs ou rationnels, possèdent un nombre infini d’éléments d’ordre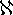 
o.
– L’infini continu qui a des bornes. Il est noté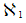 
Exemple : L’ensemble [ 0 ; 1 ] des nombres compris entre la borne 0 et la borne 1. L’ensemble des Réels est un infini continu.
II°/ Les symboles :
- La lemniscate ∞ représente un huit couché ou huit paresseux. Il est à rapprocher du ruban de Möbius et de son parcours infini. Ce symbole était utilisé par les Romains pour représenter 1000, puis un grand nombre. En 1665, John Wallis, professeur à Oxford, il utilisa ce symbole pour désigner l’infini pour la première fois dans » Arithmetica Infinitorum « . Mais, il ne fut généralisé qu’en 1713 grâce à son adoption par Bernoulli.
- Autre symbole plus courant : les trois points … . Par exemple, pour définir l’ensemble des nombres entiers : = {0, 1, 2, 3 …}.
- La cardinalité (taille) de l’infini est symbolisée par la première lettre de l’alphabet hébreux : Aleph (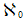). C’est Cantor d’origine juive qui a donné ce nom.
III°/ Les très grands nombres :
Un site pour s’amuser avec les très grands nombres, le Googology Wiki : en Français ou en Anglais.