Visiteurs : 259

I°/ Équations :
II°/ Carrés magiques :
III°/ Avec des dés :
IV°/ Calculatrice :
V°/ Géométrie :
VI°/ Tour de cartes :
VII°/ Pliage, construction et tour de magie :

I°/ Équations :

1°/ Forçage !

Procédure	Exemple	Explications
Choisir un nombre entier	15	n
Prendre le suivant	16	n+1
Ajouter les deux	15+ 16=31	n+n+1=2n+1
Ajouter 9 à ce résultat	9+31=40	2n+1+9=2n+10
Diviser par 2
Soustraire le nombre de départ	20 – 15 = 5	n+5 – n = 5
Le magicien annonce votre résultat 5 !

Si le magicien veut obtenir un nombre p de son choix à la fin

Procédure	Exemple	Explications
Choisir un nombre entier	15	n
Prendre le suivant	16	n+1
Ajouter les deux	15+ 16=31	n+n+1=2n+1
Ajouter 2p – 1 à ce résultat	(2x7)-1 +31=44	2n+1+2p-1=2n+2p
Diviser par 2	$\frac{44}{2}=22$	$\frac{2n+p}{2}=n+p$
Soustraire le nombre de départ	22 – 15 = 7	n+p – n = p
Le magicien annonce votre résultat p !

2°/ Trouver X (et Y) :

Procédure	Exemple	Explications
1) Pensez à deux nombres entiers (de 1 à 10)	5 et 3	a et b avec a ≥ b
2) Faites la somme de ces nombres	5+3=8	a+b
3) Multipliez le résultat par 10	8×10=80	10(a+b)=10a+10b
4) Ajoutez le plus grand nombre de départ	80+5=85	10a+10b+a=11a+10b=10(a+b)+a
5) Soustrayez le plus petit nombre de départ	85-3=82	11a+10b-b=11a+9 b=10(a+b)+(a-b)
6) Dites-moi le nombre N obtenu et je vous dirai vos deux nombres de départ !
Grand nombre de départ a = moyenne du chiffre des unités avec le nombre de dizaines de N	$\frac{8+2}{2}=5$	$\frac{(a+b)+(a-b)}{2}=a$
Petit nombre de départ b = grand nombre de départ moins le chiffre des unités du résultat N.	5-2=3	a – (a-b) = b ou alors $\frac{(a+b)-(a-b)}{2}=b$

Pour épater un peu plus votre auditoire, ce tour peut se faire avec des nombres entre 1 et 100. Le spectateur peut alors se munir d’une calculatrice.

Procédure	Exemple	Explications
1) Pensez à deux nombres entiers (de 1 à 10ⁿ)	6 524 et 2 023 (n=4)	a et b avec a ≥ b
2) Faites la somme de ces nombres	6524+2023=8547	a+b
3) Multipliez le résultat par 10ⁿ	8547×10⁴=85 470000	10ⁿ(a+b)= 10ⁿ a+10ⁿ b
4) Ajoutez le plus grand nombre de départ	85 470000+6524=85 476524	10ⁿ a+10ⁿ b +a=10ⁿ(a+b)+a
5) Soustrayez le plus petit nombre de départ	85 476524-2023=85 474501	10ⁿ(a+b)+a -b=10ⁿ(a+b)+(a-b)
6) Dites-moi le nombre N obtenu et je vous dirai vos deux nombres de départ !
Grand nombre de départ a = moyenne du chiffre des unités avec le nombre de dizaines de N	$\frac{8 547+4 501}{2}=6 524$	$\frac{(a+b)+(a-b)}{2}=a$
Petit nombre de départ b = grand nombre de départ moins le chiffre des unités du résultat N.	6 524-4 501=2 023	a – (a-b) = b ou alors latex]\frac{(a+b)-(a-b)}{2}=b[/latex]

3°/ Ne pas perdre la face :

Procédure	Exemple	Explications
1) Faire lancer les deux dés par un spectateur	5 et 3	a et b
2) Multiplier les nombres des faces supérieures	5×3=15	ab
3) Multiplier les nombres des faces inférieures	2×4=8	(7-a)(7-b)=49-7b-7a+ab
4) Multiplier le 1er nombre de la face supérieure avec le 2ème nombre de la face inférieure	5×4=20	a(7-b) = 7a-ab
5) Multiplier le 1er nombre de la face inférieure avec le 2ème nombre de la face supérieure	2×3=6	b(7-a) = 7b-ab
6) Additionner les 4 produits précédents	15+8+20+6=49	ab + 49-7b-7a+ab + 7a-ab + 7b-ab=49
7) Faire annoncer le résultat par le spectateur. On trouve 49 !

De manière générale, si on prend n dés à 6 faces, il y aura 2ⁿ produits différents à effectuer et le total vaudra toujours 7ⁿ.

Nombre de dés	Résultat final
2	7² = 49
3	7³ = 243
4	7⁴ = 2 401

4°/ La grille :

1	¤	2	?	3	?	4	?	5	¤	6	?	7	?
8	?	9	¤	10	?	11	?	12	¦	13	8	14	¤
15	?	16	?	17	?	18	¤	19	?	20	†	21	?
22	?	23	?	24	¤	25	†	26	8	27	¤	28	?
29	¦	30	?	31	¦	32	?	33	?	34	†	35	?
36	¤	37	?	38	?	39	8	40	?	41	?	42	¦
43	?	44	?	45	¤	46	?	47	?	48	?	49	?
50	?	51	8	52	?	53	?	54	¤	55	?	56	?
57	8	58	?	59	?	60	¦	61	†	62	?	63	¤
64	?	65	†	66	?	67	?	68	8	69	?	70	?
71	?	72	¤	73	8	74	?	75	¤	76	¦	77	?
78	?	79	?	80	?	81	¤	82	?	83	?	84	8
85	?	86	¦	87	?	88	?	89	?	90	¤	91	?
92	¦	93	?	94	¤	95	?	96	?	97	?	98	?
99	¤

Procédure	Exemple	Explications
Le magicien demande à tout son auditoire de choisir un nombre à 2 chiffres.	85	Un nombre à deux chiffres s’écrit 10d + u
Faire ensuite la somme des chiffres de ce nombre.	8+5 = 13	10d + u
Soustraire ce résultat au nombre de départ.	85-13=72	10d + u – (d + u )=9d (multiple de 9)
Chaque spectateur cherche dans la grille le symbole associé à son résultat.
Le magicien dévoile alors le symbole sur son papier : ¤		Mettre le même symbole pour tous les multiples de 9

5°/ L’addition fulgurante :

Procédure	Exemple	Explications
1) Ecrire un nombre A à 5 chiffres	56 108
2) Ecrire un autre nombre B à 5 chiffres en dessous	74 925
3) J’écris un nombre C à 5 chiffres en dessous	25 074	Complément à 9 de chaque chiffre : B+C = 99 999
4) Ecrire encore un autre nombre D à 5 chiffres en dessous	64 232
5) J’écris un autre nombre E à 5 chiffres en dessous	35 767	Complément à 9 de chaque chiffre : D+E = 99 999
6) Additionner les 4 nombres	256 106	A+B+C+D+E = A + 200 000 – 2
7) – le résultat commence toujours par un 2 – les 3 chiffres suivants sont les 3 premiers chiffres du 1er nombre – les deux derniers chiffres du résultat sont les deux derniers chiffres du 1er nombre auquel on enlève 2

6°/ Neuf-neuf :

Procédure	Exemple	Explications
Un spectateur choisit deux nombres à 2 chiffres	48 et 27	n et m
Il les multiplie	48×27=1296	nxm
Le magicien choisit lui aussi un nombre à 2 chiffres	72	Choisir le complément à 99 du 2ème nombre : 99-27 = 72 = 99 – m
Il demande au spectateur de multiplier son 1er nombre par celui-ci	48×72=3456	nx(99-m)
Puis, d’effectuer la somme des deux produits	1296+3456=4752	nxm + nx(99-m) = n(m + 99 – m) = 99n
Le magicien donne rapidement le résultat sans effort !	Centaine = 47 = 48-1 Unité = 52 = 99-47	99n = 100(n-1)+99-(n-1) = 100n-100+99-n+1 Centaine = n-1 Unité = 99-(n-1)

7°/ Les sommes de Léo :

Procédure	Exemple	Explications
Choisir secrètement 3 nombres entiers	4 ; 12 et 17	a, b et c
Faire toutes les sommes possibles 2 à 2 de ces 3 nombres	4+12=16 ; 4+17=21 et 12+17=29	Il y a 3 somme possibles
Annoncer ces 3 sommes au magicien	16 ; 21 ; 29	a+b ; a+c et b+c
Le magicien donne rapidement le résultat sans effort ! – Faire la moyenne de ces 3 sommes – Soustraire cette moyenne à chacune des 3 sommes du spectateur	$\frac{16+21+29}{2}=33$ 33-16=17 ; 33-21=12 et 33-29=4	a+b + a+c + b+c = 2(a + b +c) $\frac{a+b+a+c+b+c}{2}-(a+b)=a+b+c-a-b=c\\\frac{a+b+a+c+b+c}{2}-(a+c)=a+b+c-a-c=b\\\frac{a+b+a+c+b+c}{2}-(b+c)=a+b+c-b-c=a$

8°/ Dr Stone :

Procédure	Exemple	Explications
Choisir deux chiffres entre 1 et 9	8 et 3	a et b
Il demande de poser ou d’effectuer rapidement l’opération suivante à la main ou avec une calculatrice	83×87	1er nombre = 10a+b 2ème nombre = 10a + 10-b
Le magicien donne le résultat quasi-instantanément	7221 72 = 8 x 9 21 = 3 x 7	(10a+b)(10a + 10-b)=100a²+ 100a – 10ab + 10ba + 10b – b² =100a(a+1)+b(10-b)
Le magicien doit proposer un produit vérifiant les conditions suivantes : • le chiffre des dizaines est le même dans chaque facteur du produit : • les chiffres des unités sont des compléments à 10 :	83 x 87 3+7=10	a(a+1) est le produit de 2 entiers consécutifs b(10-b) est le produit des deux chiffres des unités b et 10-b compléments à 10

9°/ Multiplication fulgurante : les nombres n-parasites

Un spectateur tire au hasard le nombre parmi les 9 proposés (colonne 10n+u), et magicien demande d’effectuer la multiplication par 4, soit en la posant, soit avec une calculatrice.

Le magicien dévoile quasi-instantanément le résultat : Ex : 179 487×4 = 717948

Explication : pour les nombres à 5 chiffres, il suffit de déplacer le chiffre des unités devant le nombre suivi d’un zéro. Ex : 25 641 x 4 = 102 564

pour les nombres à 6 chiffres, il suffit de déplacer le chiffre des unités devant le nombre et c’est tout. Ex : 153 846 x 4 = 615 384

u	n	10n + u		4(10n+u)
1	2564	25641	x 4 =	102564
2	5128	51282	x 4 =	205128
3	7692	76923	x 4 =	307692
4	10256	102564	x 4 =	410256
5	12820	128205	x 4 =	512820
6	15384	153846	x 4 =	615384
7	17948	179487	x 4 =	717948
8	20512	205128	x 4 =	820512
9	23076	230769	x 4 =	923076

De tels nombres sont appelés nombres parasites. Ce sont des entiers naturels qui, lorsqu’ils sont multipliés par un certain nombre entier u compris entre 2 et 9, voient leur suite de nombre inchangée, excepté pour le chiffre des unités qui est déplacé en début d’écriture.

u	P_u	u x P_u
2	105 263 157 894 736 842	210 526 315 789 473 684
3	1 034 482 758 620 689 655 172 413 793	3 103 448 275 862 068 965 517 241 379
4	102 564	410 256
5	142 857	714 285
6	10 169 491 525 423 728 813 559 932 203 389 830 508 474 576 271 186 440 677 966	61 016 949 152 542 372 881 355 993 220 338 983 050 847 457 627 118 644 067 796
7	1 014 492 753 623 188 405 797	7 101 449 275 362 318 840 579
8	1 012 658 227 848	8 101 265 822 784
9	10 112 359 550 561 797 752 808 988 764 044 943 820 224 719	91 011 235 955 056 179 775 280 898 876 404 494 382 022 471

Une vidéo pour comprendre les nombres n-parasites (un peu rude) :

10°/ Nombre phénix :

Le magicien vante les propriétés magiques du nombre 142857 tel un phénix.

Il demande à un spectateur les calculs suivants :

Procédure	Exemple
Choisir un nombre entier	52
Multiplier par 142 857	52×142 857=7 428 564
Prendre les 6 derniers chiffres et les ajouter avec ceux de devant	7+428 564=428 571
Utiliser le cercle pour diviser par le nombre situé en dessous du 1er chiffre de votre produit précédent : 1er chiffre = 4 donc on divise par 3	$\frac{428 \ 571}{3}=$ 142 857

142857×r donne la permutation cyclique des chiffres car r<7 :

142857×1=142857

142857×2=285714

142857×3=428571

142857×4=571428

142857×5=714285

142857×6=857142

142857×7=999999

Explications	Exemple
Soit N un nombre entier. Il peut s’écrire N = 7q+r où 0 ≤ r <7 (division euclidienne par 7)	52 = 7×7+3 avec q=7 et r = 3
Donc : 142857×N = 142 857×(7q+r) = q×(7×142 857) + 142 857×r = q×999 999 + 142 857×r	142 857×52 = 7×999 999 + 3×142 857 = 7×999 999 + 428 571
Donc : 142857×N = q×1 000 000 + 142 857×r – q	142 857×52 = 7×1 000 000 + 428 571 – 7 = 7 000 000 + 428 564 = 7 428 564
Donc : q×1 000 000 + 142 857×r – q – q×1 000 000 + q = 142 857×r	7 428 564 – 7 000 000 + 7 = 428 571 = 3×142 857
Et enfin : = $\frac{142 \ 857\times q}{q}=$ 142 857	$\frac{428 \ 571}{3}=\frac{3\times 142 \ 857}{3}=$ 142 857

11°/ Des chiffres et des lettres :

Procédure	Exemple	Tableau
Le spectateur choisit un nombre parmi les trois premières colonnes	4
Il écrit ce nombre en toutes lettres	QUATRE
Chaque lettre est associée avec un nombre. Si la case est grisée le nombre sera négatif. Il additionne ainsi la valeur des lettres	Q+U+A+T+R+E = -9+4+19-5+3-8 = 4
Il trouvera toujours le nombre qu’il a choisi au départ !!! Etonnant non ?

Il faut exactement 16 lettres différentes pour écrire ces 9 chiffres qui sont autant d’inconnues pour notre système d’équations que voici :

U+N=1

D+E+U+X=2

T+R+O+I+S=3

Q+U+A+T+R+E=4

C+I+N+Q=5

S+I+X=6

S+E+P+T=7

H+U+I+T=8

N+E+U+F=9

9 équations pour 16 inconnues imposent des paramètres. On peut le programmer sur tableur. Il y a plusieurs solutions possibles.

	U	N	D	E	X	T	R	O	I	S	Q	A	C	P	H	F
1^ière solution	4	3	1	8	5	5	3	4	7	6	9	19	10	26	2	16
2^ième solution	4	-3	1	-8	5	-5	3	4	7	-6	-9	19	10	26	2	16

12°/ Neuf en date :

Procédure	Exemple
Choisir une date sous la forme JJMMAAAA (mettre un 0 devant si le jour est inférieur à 10).	31/07/1974 → 31071974
Mélanger les 8 chiffres pour obtenir un autre nombre à 8 chiffres	74103719
Soustraire le plus grand au plus petit	74103719-31071974=43031745
Ajouter les chiffres de ce nombre jusqu’à n’obtenir qu’un seul chiffre	4+3+0+3+1+7+4+5=27 puis 2+7=9
Le magicien annonce sa prédiction : 9	On aura toujours un multiple de 9

On peut faire le tour avec d’autres nombres puisque la preuve est la même.

13°/ Un pour tous… :

Procédure	Exemple	Explications
Choisir un nombre de 4 chiffres tous différents.	5941	1000m+100c+10d+u avec m, c, d et u tous différents.
Trouver tous les nombres que l’on peut écrire avec ces chiffres.	1459 ; 1495 ; 1549 ; 1594 ; 1945 ; 1954 ; 4159 ; 4195 ; 4519 ; 4591 ; 4915 ; 4951 ; 5149 ; 5194 ; 5419 ; 5491 ; 5914 ; 5941 ; 9145 ; 9154 ; 9415 ; 9451 ; 9514 ; 9541	Il y a 4! = 1×2×3×4 = 24 nombres possibles que l’on peut écrire avec ses 4 chiffres. Il y a 3! = 6 nombres qui débute par le chiffre m (une fois le 1^ier chiffre des milliers choisis, il reste 3 chiffres à combiner), idem pour les autres chiffres. Il y a 6 nombres commençant par 1 …
Faire la somme de tous ces nombres	1459+1495+…+9514+9541 = 126 654	Quand on fait la somme des 24 nombres, on retrouve 6 fois chaque chiffre m, d, c et u. Il y a = 1000(6m+6d+6c+6u) + 100(6m+6d+6c+6u) + 10(6m+6d+6c+6u) + (6m+6d+6c+6u) = 6 666(m+d+c+u)
Diviser cette somme par la somme des chiffres du nombre choisi.	5+9+4+1=19 donc : $\frac{126 \ 654}{19}=$ 6 666	$\frac{6 666(m+d+c+u)}{m+d+c+u}=$ 6 666
Le magicien avait prédit ce résultat dès le début : 6 666.

14°/ Triacontakaihepta :

Procédure	Exemple	Explications
Le spectateur choisit un nombre à 3 chiffres identiques.	444	N = 100a+10a+a = 111a avec a = 4
Il calcule la somme de ses chiffres.	4+4+4=12	a+a+a = 3a
Il divise son nombre de départ par cette somme.	$\frac{444}{12}=37$	$\frac{111a}{3a}=\frac{111}{3}=37$
Le magicien avait prédit ce résultat dès le début : 37.

On peut réaliser le même tour avec des nombres à 9 chiffres identiques.

Procédure	Exemple	Explications
Le spectateur choisit un nombre à 9 chiffres identiques.	444 444 444	N = 111 111 111a avec a = 4
Il calcule la somme de ses chiffres.	9×4 = 36	9a
Il divise son nombre de départ par cette somme.	$\frac{444 \ 444 \ 444}{36}=12 \ 345 \ 679$	$\frac{111 \ 111 \ 111a}{9a}=\frac{111 \ 111 \ 111}{9}=12 \ 345 \ 679$
Pour obtenir un meilleur effet magique, le magicien peut prédire le chiffre 8 et annoncer ainsi que c’est le chiffre manquant dans le résultat !

15°/ Les bâtons magiques :

8	7	7	3	6	9	8	8	8	8	2	9	9	4	9	9	6	4	6	6	7	7	9	7	4	0	3	5	4	5	8	1	2	3	6	7	5	2	9	6	3	4	1	8	8	9	5	5	6	5	9	7	7	9	8
7	6	5	6	4	9	3	5	6	9	8	5	1	9	7	4	3	6	9	7	8	3	2	4	8	9	7	5	5	7	2	9	9	9	5	7	8	7	8	6	8	7	8	4	8	0	9	6	8	4	3	9	2	6	1
7	6	8	9	3	0	4	4	7	6	3	9	2	8	4	6	2	4	7	8	4	0	5	0	2	9	1	2	1	6	3	0	6	1	0	9	8	9	9	2	3	1	6	2	2	6	9	6	9	9	0	0	6	8	2
3	5	6	9	8	0	7	5	4	1	8	4	8	5	2	5	9	8	3	5	3	8	7	7	6	9	8	8	9	6	8	8	7	6	7	4	5	9	1	6	7	7	9	6	2	9	4	7	4	9	6	2	9	3	9

Procédure

Exemple

Explications

Prenez 4 colonnes de chiffres, n’importe lesquelles, et additionnez les 4 nombres ainsi créer.

   9646      9740
+ 4369 + 2489
+ 6247     + 5029
+ 5983     + 7769
26 245     25 027

La somme des 1er, 2nd et 4ème chiffres fait toujours 18.

Exemples n°1 : 9+4+5 = 6+3+9 = 4+6+8 = 6+9+3 = 18

Exemples n°2 : 9+2+7 = 7+4+7 = 4+8+6 = 0+9+9 = 18

Le magicien avait prédit ce résultat sans effort.

26 245 = 20 000 + 6 247 – 2

18 000+1800+180+18+3^ième nbre = 19 998+4193 = 20 000 + 3^ième nbre – 2

La somme débute par un 2 suivie du 3^ième nombre moins 2.

16°/ Les pions de Diophante :

Procédure

Exemple

Explications

Vous devez choisir un nombre blanc ou bleu dans chacune des 10 colonnes.

Exemple n°1

Exemple n°2

Exemple n°3

59	12	57	86	31	63	65	92	87	48
50	3	48	77	22	54	56	83	78	39

→ la somme des nombres blancs fait 600

→ il faut enlever 9 au nombre blanc pour obtenir le nombre bleu qui est en dessous.

Faire la somme de ces 10 nombres.

Somme n°1 = 564 (il y a 6 nombres blancs et 4 bleus).

Somme n°2 = 573 (il y a 7 nombres blancs et 3 bleus).

Somme n°3 = 546 (il y a 4 nombres blancs et 6 bleus).

→ le chiffre des centaines est toujours 5

→ le chiffre des dizaines est le nombre de nombres blancs

→ le chiffre des unités est le nombre de nombres bleus ou le complément à 10 du précédent.

Le magicien avait prédit ce résultat sans effort.

Démonstration : soit B = nombre de nombres blancs et E = nombre de nombres bleus. Avec B + E = 10 ou B = 10 – E

Somme des 10 nombres = somme des 10 nombres blancs – 9 fois le nombre de nombres bleus = 600 – 9E = 500 + 100 – 10E + E = 500 + 10(10 – E) + E = 500 + 10B + E

17°/ Le grand écart :

Procédure

Exemple

Choisir des nombres dans l’ordre croissant.

-34

-18

-5

106

137

181

202

206

Calculer les écarts entre chaque nombre.

=-18–34=16

=-5–18=13

=44–5=49

=82-44=38

=106-82=24

=137-106=31

=181-137=44

=202-181=21

=206-202=4

Additionner tous ces écarts.

16 + 13 + 49 + 38 + 24 + 31 + 44 + 21 + 4 = 240

Donner seulement le 1^ier et le dernier.

-34 et 206

Le magicien avait prédit ce résultat sans effort.

206 – (-34) = 240

Il faut cacher les 3 premières étapes au magicien.

Explications : x₂-x₁+ x₃-x₂+ x₄-x₃ +…+ x_n-1-x_n-2+ x_n-x_n-1= x_n-x₁

18°/ La table de multiplication magique :

Procédure

Exemple

Explications

Un spectateur de choisit 5 nombres au hasard de sorte qu’il n’y ait qu’un seul nombre coché par ligne et par colonne.

x	19	-18	-3	6	-9
5	95	-90	-15	30	-45
-18	-342	324	54	-108	162
-20	-380	360	60	-120	180
-13	-247	234	39	-78	117
1	19	-18	-3	6	-9

Le magicien demande ensuite de faire le produit de ces 5 nombres.

-90 x 54 x (-380) x (-78) x (-9) = 1 296 453 600

Il suffit de multiplier tous les nombres verts.

bf × dg × ah × ci × ej = a×b×c×d×e×f×g×h×i×j

Le magicien avait prédit ce résultat sans effort car il a effectué le calcul au préalable.

-90 x (-18) x (-3) x 9 x (-9) x 5 x (-18) x (-20) x (-13) x 1 = 1 296 453 600

19°/ 111 111 :

Procédure

Exemple

Explications

Choisir un nombre à 3 chiffres entre 100 et 999

658

N = 100c+10d+u

Multiplier par 3

658×3=1974

Multiplier par 7

1974×7=13818

Multiplier par 37

13818×37=511266

Puis 11, puis 13. Annoncer le résultat au magicien.

511266×11=5623 926 et 5623926×13 = 73 111038

3×7×11×13×37 = 111 111

1^ier exemple :

. 1 1 1 1 1 1

. x 234

. 4 4 4 4 4 4

. 3 3 3 3 3 3

. 2 2 2 2 2 2

= 2 5 9 9 9 9 7 4

u = 4

d = 10+7 – 4 = 13

4+3=7 donc r=0

c = 9 – (4+3+0) = 2

N = 234

2^ième exemple :

. 1 1 1 1 1 1

. x 658

. 8 8 8 8 8 8

. 5 5 5 5 5 5

. 6 6 6 6 6 6

= 7 3 1 1 1 0 3 8

u = 8

d = 10+3 – 8 = 15

8+5=13 donc r=1

c = 10n – (8+5+1) = 20-14 = 6 = 7–1

N = 658

Explication :

. 1 1 1 1 1 1

. x c d u

. u u u u u u

. d d d d d d

. c c c c c c

= k ………… C D U

u = U

d = 10+D – U = unité du résultat

u+d = 10r + m donc r = 0 ou 1

c = 10n –(u+d+r)

= |C–D–U–r|

= k – r (pas tjs)

20°/ Un nombre têtu :

Procédure

Exemple

Explications

Choisir un nombre entier

Ajouter son sextuple

32 + 6×32 = 224

p + 6p = 7p

Soustraire 6

224-6 = 218

7p – 6

Diviser par 7

\frac{218}{7}\approx 31,142 \ 857 \ 14...

\frac{7p-6}{7}=p-\frac{6}{7}=p-1+\frac{1}{7}\\=p-1+0,142 \ 857 \ 142 \ 857...

Conserver les 6 premiers chiffres après la virgule

142 857

Un nombre têtu est le motif du développement décimal de 1/k où k est un nombre premier long. Ici k = 142 857

1er effet : Multiplier par le nombre précédent par un nombre entre 1 et 6

142 857×3 = 428 571

142 857×1 = 142 857142 857×2 = 285 714

142 857×3 = 428 571

142 857×4 = 571 428

142 857×5 = 714 285

142 857×6 = 857 142

142 857×7 = 999 999

Quand on multiplie un nombre têtu à m chiffres par 1, 2, …, m (ici m=6) alors le produit est une permutation circulaire de ces m chiffres.

Le spectateur supprime un chiffre de son choix

Le 5 de qui laisse : 42 871

142857 est divisible par 9 car 1+4+2+8+5+7=27

Il annonce la somme des chiffres qu’il reste au magicien

4+2+8+7+1 = 22

Le magicien sait quel nombre il manque en faisant simplement 27 – 22 = 5

Le magicien donne immédiatement le chiffre manquant : 27 – (somme du spectateur)

2ème effet : Séparer le nombre à 6 chiffres en deux nombres à 3 chiffres et effectuer la somme

142+857 = 999

Théorème de MIDY : Si on sépare en deux un nombre têtu à p-1 chiffres alors la somme des deux nombres à chiffres vaut

Ici : p=7 et le nombre têtu est 142857 à 6 chiffres donc

142+857 =

Le magicien donne immédiatement la somme : 999

21°/ Le calendrier :

Procédure	Exemple	Explications
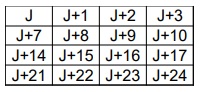
Sur un calendrier tracer un carré 4×4 entourant 16 dates de son choix.		La somme totale des 16 dates est : J+J+1+J+2+…+J+23+J+24 = 16J+1+2+…+23+24 = 16J + 192 Ici J = 6
Dans ce carré, choisir un seul nombre par ligne et par colonne.		La somme des 4 dates = $\frac{16J+192}{4}=4J+48$
Additionner les 4 dates.	7+13+23+29 = 72	$4J+48=4\times 6+48=$ 72

22°/ Le billet de banque en € :

Procédure

Exemple

Donner le numéro d’identification au verso d’un billet émis après 2013 (ils commencent par 2 lettres) en haut à droite excepté le dernier chiffre.

Le magicien note le numéro, réfléchit quelques secondes et donne le chiffre manquant.

U → 21 et A → 1 donc on prend les 9 premiers chiffres précédés de 211 pour obtenir un nombre à 11, 12 ou 13 chiffres : 211 405631689

On additionne tous ces chiffres : 2+1+1+4+0+5+6+3+1+6+8+9 = 46

Puis 4+6 = 10 puis 1+0 = 1 = r

Le dernier chiffre se calcule ainsi : 7 – 1 = 6 qui est bien le dernier chiffre !

Chaque lettre est égale à son rang.

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26

Le dernier chiffre se calcule ainsi :

• si 0 = r = 6 alors clé = 7 – r

• si r =7 alors clé = 9

• si r =8 alors clé = 8

23°/ Date de naissance 01 :

Procédure	Exemple	Explications
Le magicien donne la calculatrice à un spectateur et lui demande une date.	14/03/1995	Notons j/m/a la date de naissance où a représente les 2 derniers chiffres de l’année.
1. Ajouter 18 au mois de naissance	3+18 = 21	1. 18+m
2. Multiplier le résultat par 25	21×25 = 525	2. 25×(18+m) = 450+25m
3. Soustraire 333	525-333 = 192	3. 25m+450-333 = 25m+117
4. Multiplier le résultat par 8	192×8 = 1536	4. 8×(25m+117) = 200m+936
5. Soustraire 554	1536-554 = 982	5. 200m+936-554 = 200m+382
6. Diviser le résultat par 2 :		6. {200m+382}/2 = 100m+191
7. Ajouter le jour de naissance	491+14 = 505	7. 100m+191+j
8. Multiplier le résultat par 5	505×5 = 2525	8. 5×(100m+j+191) = 500m+5j+955
9. Ajouter 692	2525+692 = 3217	9. 500m+5j+955+692 = 500m+5j+1647
10. Multiplier le résultat par 20	3217×20 = 64340	10. 20×(500m+5j+1647) = 1000m+100j+32940
11. Ajouter les deux derniers chiffres de l’année de naissance	64340+95 = 64 435	11. 10000m+100j+23940+a
12. Le magicien effectue de tête la soustraction par 32940 on voit apparaître dans l’ordre la date de naissance complète Mois-jour-année.	64 435-32 940 = 31 495	12. 10000m+100j+a+32940-32940 = 10000m+100j+a

24°/ La magie du 9 :

Procédure	Exemple	Explications
1) Pensez à un nombre de 1 à 10 (ou plus grand, mais vous aurez peut-être besoin d’une calculatrice)	17	On choisit N
2) Multipliez votre nombre par 3	17×3 = 51	N × 3 =3 N
3) Ajoutez 6	51 + 6 = 57	3N +6
4) Multipliez à nouveau par 3	57×3 = 171	3 × (3N + 6) = 9N + 18 = 9 (N +2 ) et on a déjà un multiple de 9
5) Si vous le souhaitez, multipliez votre résultat par 2	171×2 = 342 ou 171	9 (N +2) ou 2×(9+18) = 18N + 36 = 9(2N + 4)
6) Faites la somme des chiffres de votre nombre. Si le résultat est un nombre à un chiffre, alors arrêtez-vous.	3 + 4 + 2 = 9 ou 1 + 7 + 1 = 9 donc on s’arrête
7) Si la somme est un nombre à 2 chiffres, faites alors la somme de ces chiffres.
8) Concentrez-vous sur votre réponse	c’est le 9 !	On aura toujours un multiple de 9

25°/ Gauss n’a qu’à bien se tenir… :

Procédure	Exemple	Explications
Demander à un spectateur de choisir un nombre entier.	257	n
Lui demander de calculer la somme des 10 entiers consécutifs à partir du nombre choisi, avec une calculatrice.	257+258+259+260+261+262+263+264+265+266 = 2615	n + n+1 + n+2 + n+3 + n+4 + n+5 + n+6 + n+7 + n+8 + n+9 = 10n + 45
Le magicien donne la réponse plus rapidement que la calculatrice : 257 + 4 = 261 et on rajoute 5 après : 2615

26°/ Multiplier par 999 :

Procédure	Exemple	Explications
Demander à un spectateur de choisir un nombre entier de 3 chiffres.	257	n
Avec une calculatrice lui demander de le multiplier par 999.	257 x 999 = 256 743	999n = 1000n – n = 1000n – 1000 + 1000 – n = 1000(n-1) + 1000 – 1 – n + 1 = 1000(n-1) + 999 – (n-1)
Le magicien donne la réponse plus rapidement que la calculatrice : 257 – 1 = 256 (Ce qui donne le nombre de milliers) et 999 – 256 = 743 (les compléments à 9 des trois chiffres précédents). Si le nombre de départ a 2 chiffres, penser à mettre un zéro fictif devant le nombre à deux chiffres (exple. 034).

27°/ Mentalisme :

Procédure	Exemple	Explications
Le magicien demande à un spectateur de penser secrètement à une des 52 cartes du jeu (exceptés les jokers).	5 de cœur	n = 5 et c = 8
Ajouter la valeur de la carte qui suit (si le spectateur a choisi un roi, il ajoutera 14).	5 + 6 = 11	n + n+1 = 2n + 1
Multiplier le résultat par 5.	11 x 5 = 55	(2n + 1) x 5 = 10n + 5
Ajouter le chiffre correspondant à la couleur de sa carte.	55 + 8 = 63	10n + 5 + c
	Le magicien enlève 5 au résultat : 63 – 5 = 58 = 5×10 + 8	10n + 5 + c – 5 = 10n + c Le nombre de dizaines est n est la valeur de la carte et le chiffre des unités est la couleur !
Annoncer le résultat au magicien qui retrouve instantanément la carte !

28°/ Date de naissance 02 :

Procédure	Exemple	Explications
Le magicien demande à un spectateur d’effectuer les calculs suivants avec sa date de naissance (jour et mois seulement).	12 mai, jour de naissance de Maryam Mirzakhani (en 1977).	Notons J le jour de naissance et M le mois.
Multiplier le jour par 2	12 x 2 = 24	J x 2
Ajouter 5	24 + 5 = 29	Jx2 + 5
Multiplier le tout par 50	29 x 50 = 1450	(Jx2 + 5)x50
Ajouter le N° du mois	1450 + 5 = 1455	(Jx2 + 5)x50 + M = 100J + 250 + M
Annoncer votre résultat au magicien qui retrouve quasi-instantanément votre date de naissance !	1455 – 250 = 1205 soit le 12/05 BINGO !	Il suffit d’enlever 250 au résultat pour voir apparaître le jour en nombre de centaines et le mois en unités et dizaines !

29°/ Triangles absolus :

Introduction : Un triangle absolu est une pyramide de nombres entiers de 1 à n de telle sorte que la différence de deux nombres voisins sur la même ligne en valeur absolue donne le nombre à la ligne du dessus.

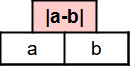
L’enjeu de ce tour impromptu est de conduire le spectateur vers le nombre qu’il aura choisi au préalable !

Procédure	Exemple
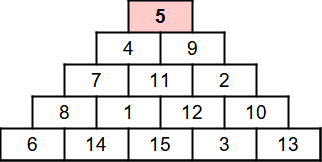
Le magicien demande à un spectateur de choisir un nombre à 2 chiffres (nombre fétiche, date d’anniversaire,…).	23
Il montre au spectateur une pyramide à 3 étages vierge.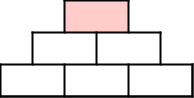
Très rapidement, le magicien remplit la dernière ligne avec 3 nombres.
Il invite le spectateur à compléter la pyramide en effectuant les différences en valeur absolue de deux nombres voisins. 115 – 46 = 69 puis 138 – 46 = 92 et enfin 92 – 69 = 23
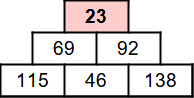Le magicien apprend par cœur la pyramide suivante (finalement la dernière ligne suffit). A gauche : (23 x 10) / 2 = 230/2 =115 Au milieu : 23 x 2 = 46 A droite : 115 + 23 = 138

D’autres triangles absolus d’ordre 4 et 5 :

30°/ Table de multiplication :

Procédure

Exemple

Le magicien fourni la table de multiplication ci-contre.

Demandez de dessiner un hexagone sur la table, puis d’additionner les nombres de ses sommets.

En partageant le résultat, vous pouvez en déduire le numéro central de l’hexagone.

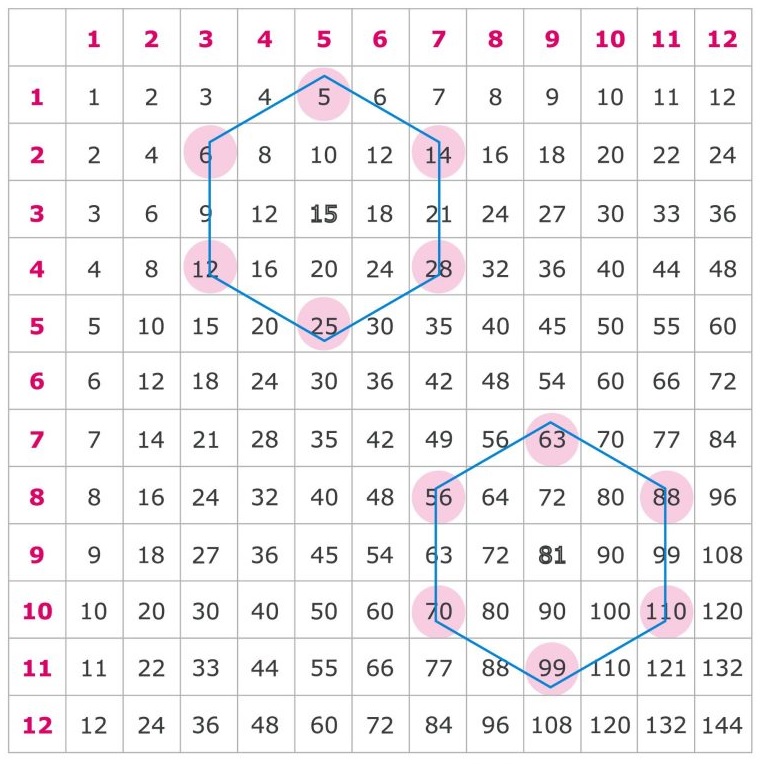Comment? Divisez simplement la somme par 6.

5 + 14 + 28 + 25 + 12 + 6 = 90 et 90/6 = 15

63 + 88 + 110 + 99 + 70 + 56 = 486 et 486/6 = 81

31°/ Nombres tressés :

Procédure	Exemple	Explications
1/ Demander à un spectateur de choisir un nombre entier de 3 chiffres.	748	N = 100c + 10d + u
Avec une calculatrice lui demander : 2/ Prendre 100 fois la somme du chiffre des unités et des dizaines.	100x(4+8) = 1 200	100(d + u)
3/ Prendre 10 fois la somme du chiffre des unités et des centaines.	10x(7+8) = 150	10(c + u)
4/ Prendre la somme du chiffre des dizaines et des centaines.	7+4 = 11	c + d
5/ Effectuer la somme des 4 nombres précédents.	748 + 1 200 + 150 + 11 = 2 109	100c + 10d + u + 100d + 100u + 10c + 10u + c + d = 111 (c + d + u)
6/ La diviser par 37.	2 109/37 = 57	111 (c + d + u)/37 = 3 (c + d + u)
Le magicien donne la réponse plus rapidement que la calculatrice : Calculer la somme des chiffres du nombre du spectateur et le multiplier par 3. 3×(7+4+8) = 3×19 = 57

32°/ Le ruban de Pascal :

Procédure	Exemple	Explications
1/ Demander à un spectateur de choisir un nombre entier de 3 chiffres.	412	N = 100c + 10d + u
2/ Effectuer la somme de 5 fois le chiffre des centaines, 10 fois celui des dizaines et 1 fois celui des unités.	4×5 + 1×10 + 2×1 = 32	5xc + 10xd + 1xu = 5c + 10d + u
3/ Soustraire ce résultat au nombre de départ.	412−32 = 380	100c + 10d + u – 5c – 10d – u = 95c = 5x19c
4/ Diviser par 19.	380/19 = 20	95c/19 = 5c
Le magicien donne la réponse plus rapidement que la calculatrice : Calculer 5 fois le chiffre des centaines et c’est fini ! 5×4 = 20

A vous de jouer :

33°/ 18, 27 ou 36 :

Procédure	Exemple	Explications
1/ Demander à un spectateur de choisir un nombre entier de 2 chiffres.	41	ab Avec : a = 4 et b = 1
2/ De le multiplier par 99.	41 x 99 = 4 059	ab x 99 = 100ab – ab
3/ D’additionner tous les chiffres du résultat.	4 + 0 + 5 + 9 = 18	Millier = a Centaine = b – 1 Dizaine = 10 – a – 1 = 9 – a Unité = 10 – bSomme = a + b-1 + 9-a + 10-b = 18
Le magicien donne la réponse plus rapidement que la calculatrice : 18

Procédure	Exemple	Explications
1/ Demander à un spectateur de choisir un nombre entier de 2 chiffres.	41	ab Avec : a = 4 et b = 1
2/ De le multiplier par 999.	41 x 999 = 40 959	ab x 999 = 1000ab – ab
3/ D’additionner tous les chiffres du résultat.	4 + 0 + 9 + 5 + 9 = 27	Dix-mille = a Millier = b – 1 Centaine = 10 – 1 = 9 Dizaine = 10 – a – 1 = 9 – a Unité = 10 – bSomme = a + b-1 + 9 + 9-a + 10-b = 27
Le magicien donne la réponse plus rapidement que la calculatrice : 27

Procédure	Exemple	Explications
1/ Demander à un spectateur de choisir un nombre entier de 2 chiffres.	41	ab Avec : a = 4 et b = 1
2/ De le multiplier par 9 999.	41 x 9 999 = 409 959	ab x 9 999 = 10000ab – ab
3/ D’additionner tous les chiffres du résultat.	4 + 0 + 9 + 9 + 5 + 9 = 36	Cent-mille = a Dix-mille = b – 1 Millier = 10 – 1 = 9 Centaine = 10 – 1 = 9 Dizaine = 10 – a – 1 = 9 – a Unité = 10 – b Somme = a + b-1 + 9 + 9 + 9-a + 10-b = 36
Le magicien donne la réponse plus rapidement que la calculatrice : 36

34°/ Le mentaliste :

Procédure	Explications
1°/ Choisir un animal.
2°/ Compter le nombre de lettres qui le compose.	Soit x le nombre de lettres
3°/ Multiplier ce nombre par 2.	2x
4°/ Multiplier ce résultat par 5.	10x
5°/ Enlever 6.	10x – 6 et 10x se termine obligatoirement par un 0. Si on enlève 4, le résultat se terminera obligatoirement par 4.
6°/ Prendre le chiffre des unités.	4
7°/ Prendre la lettre qui correspond a ce chiffre : A = 1 ; B = 2 …	4 = D
8°/ Choisir un pays commençant par cette lettre.	Il y a seulement 3 les pays commençant par D : Danemark : le plus connu Djibouti Dominique
9°/ Choisir un fruit qui commence par la dernière lettre de ce pays.	Il y a seulement 5 les pays commençant par K : Kaki : connu Kiwaï Kiwano Kiwi : le plus connu Koronéïki
Je devine votre réponse : le kiwi.

II°/ Carrés magiques :

1°/ Carrés magiques 3×3 :

Demander la date de naissance d’un spectateur et fabriquer un carré magique.

Par exemple : 17 décembre 2015 cela donne 3 nombres : J=17, M=12 et D=15

29	-10	32
20	17	14
2	44	5

29+17+5 =

-10+17+44 = 51 = 3×17

J+M	J-M-D	J+D
J-M+D	J	J+M-D
J-D	J+M+D	J-M

Avec J=17, M=12 et D=15

Nombre magique = 3J

Il peut y avoir des valeurs négatives et si D=2M il y aura des valeurs identiques.

2°/ Carrés magiques 4×4 :

Demander la date de naissance d’un spectateur et fabriquer un carré magique.

Par exemple : 17 décembre 2015 cela donne 4 nombres : J=17, M=12, D=1 et U=5

17	12	1	5
0	6	16	13
6	2	11	16
12	15	7	1

17+12+1+5 = 17+6+11+1 = 35

J	M	D	U
D-1	U+1	J-1	M+1
U+1	D+1	M-1	J-1
M	J-2	U+2	D

Avec J=17, M=12, D=1 et U=5

Nombre magique = 3a

On peut aussi retrouver la somme magique sur les 4 sommets du carré et sur les 4 cases centrales, sur tout type de carré 2×2.

3°/ Cercles magiques :

Demander à un spectateur un nombre important pour lui.

Le magicien complète les 6 emplacements de ces 3 cercles concentrique, en utilisant le nombre du spectateur. La somme des 4 nombres cocycliques est toujours la même !

31+32+36+35 = 134

31+33+36+34 = 134

35+33+32+34 = 134

Somme magique = 4×31 + 10 = 134

En partant de n on peut compléter le diagramme.

Somme magique = 4n + 10

Si n = 1 alors Somme magique = 4×1 + 10 = 14

Si n = 31 alors Somme magique = 4×31 + 10 = 134

Avec 4 cercles, mettre le nombre de départ n en position 1 et ajouter 1.

Somme magique = 6n + 33

Si n = 1 alors Somme magique = 6×1 + 33 = 39

Si n = 31 alors Somme magique = 6×31 + 33 = 219

Les cercles verts et roses donnent la même somme magique.

Somme magique = 4n + 30

Si n = 1 alors Somme magique = 4×1 + 30 = 34

Si n = 31 alors Somme magique = 4×31 + 30 = 154

Six carrés magiques 4 x 4 dont la somme magique est 194.

La somme magique sur les cercles est : 776 = 4 x 194.

III°/ Avec des dés :

1°/ En 3 dés :

Procédure	Exemple	Explications
Lancer les trois dés en les cachant.	3, 6 et 2	Appelons a, b, c les faces des 3 dés.
Multipliez le résultat du 1er dé par 2 puis ajouter 5.	3×2 + 5 = 6+5 = 11	a×2 + 5 = 2a+5
Multipliez le résultat obtenu par 5 et ajoutez le résultat du 2ème dé.	11×5 + 6 = 55+6 = 61	5×(2a + 5) + b = 10a + 25 + b
Multipliez enfin ce résultat par 10 et ajoutez le résultat du 3ème dé.	61×10 + 2 = 610+2 = 612	10×(10a + b + 25) + c = 100a + 10b + 250 + c
Le magicien retrouve les faces des 3 dés avec seulement l’annonce du résultat !	612-250 = 362	Le magicien enlève 250 au résultat annoncé par le spectateur pour obtenir 100a + 10b + c – le chiffre des centaines est le 1er dé – le chiffre des dizaines est le second – le chiffre des unités est le troisième.

2°/ La tour de dés :

Procédure	Exemple	Explications
Empiler 3 dés les uns sur les autres.
Donner moi seulement la face supérieure.	Le 6
Le magicien donne instantanément la somme des 5 faces cachées entre le 1er et le 2ème dé, entre le 2ème et le 3ème dé et la face du dessous.	3×7 – 6 = 15	La somme de deux faces opposées d’un dé vaut toujours 7. Comme il y a 3 dés, cela vaut 3×7=21.
Variantes : On peut faire ce tour avec 4,5,… dés. Le magicien doit juste faire le calcul suivant : 7 x Nombre de dés – (face visible du 1er dé)

3°/ Les 5 dés magiques :

Procédure	Exemple	Explications
Voici 5 dés virtuels (on peut aussi les fabriquer).		→ Sur chaque dé, le chiffre des dizaines est le même, et leur somme fait 200 : (5+2+3+4+6)x10 = 200 = 20 centaines → Sur chaque dé, la somme du chiffre des centaines et celui des unités est constante : 11 pour le 1er dé, 8 pour le 2ème, 13 pour le 3ème, 9 pour le 4ème et 7 pour le 5ème : 11+8+13+9+7 = 48
Choisir un nombre pour chaque dé.		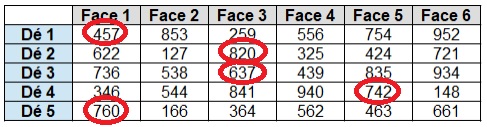→ Soient a, b, c et d les chiffres des unités. Le nombre de centaines des 5 dés donne : 100x[(11-a) + (8-b) + (13-c) + (7-d)] + 200 = 100x[(11+8+13+9+7 + 2) – (a+b+c+d)] = 100x(50 – (a+b+c+d)] Le nombre de centaines = le complément à 50 de la somme des chiffres des unités.
Additionner ses 5 nombres.	Expl 1 : 457+820+637+742+760=3416 Expl 2 : 853+127+934+346+562=2822	7+0+7+2+0 = 16 et 50-16 = 34 centaines donc 3416 3+7+4+6+2 = 22 et 50-22 = 28 centaines donc 2822
Le magicien donne instantanément la somme des 5 nombres.

IV°/ Calculatrice :

1°/ Le nombre d’Euler e :

Le nombre d’Euler e est un nombre tout aussi célèbre que le nombre pi : e ˜ 2,718281828459045…

Procédure	Exemple
Taper sur la calculatrice un nombre à 7 chiffres dont le spectateur devra se souvenir (un numéro fétiche, un nombre avec 7 fois le même chiffre, …)
Calculer l’inverse de ce nombre (en appuyant sur la touche 1/x ou x^-1 de la calculatrice)
Ajouter 1 à la réponse précédente
Élever ce nombre à la puissance du nombre de départ à 7 chiffres (en appuyant sur la touche x^y ou ^ de la calculatrice)
Le résultat final donne les 5 premières décimales exactes de e. Le magicien avait écrit ces décimales sur un papier. Magie !!!

En effet : $\displaystyle\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^{n}=e$

2°/ La magie de p :

Procédure	Exemple	Explications
1. Sur la calculatrice, taper autant de 5 que vous pouvez (10 au maximum).		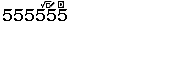555..555 = $\sum_{k=0}^{n-1}5\times 10^{k}$
2. Prenez l’inverse de ce nombre en tapant sur la touche x^-1 ou 1/x suivant les calculatrices.		$\frac{1}{\sum_{k=0}^{n-1}5\times 10^{k}}=1,800..001800..00..\times 10^{-n}$
3. Taper sur la touche « sin » de votre calculatrice (en mode degré !).		Si x tend vers 0 alors sin x = x en radian Pour convertir un angle en degrés en radians, on le multiplie par p/180 : $\frac{1\times\pi}{\sum_{k=0}^{n-1}5\times 10^{k}\times 180}=\pi\times 1,00...00100...001...\times 10^{-n-2}$
On voit apparaître le nombre pi avec 8 décimales exactes ! On peut taper sur la touche « p » de la calculatrice pour comparer les décimales.		• 3 chiffres 5 pour voir apparaître 3,14 • 12 chiffres 5 pour voir le même nombre de décimales exactes que sur une calculatrice de niveau collège : 3,1415926535

3°/ La magie du cosinus :

Procédure	Exemple
Le spectateur choisit un nombre	47
Il calcule son cosinus
Il calcule le cosinus de la réponse (Il tape à nouveau sur cos puis sur Rép ou ANS pour reprendre la valeur précédente).
Il reproduit l’opération 4 fois de plus. On obtiendra toujours : 0,9998477415

La prédiction 0,9998477415 est une valeur approchée du point fixe de la fonction f(x)=cos(x).

Si x est en degrés, ce point fixe vaut environ 0,9998477415
Si x est en radians, il vaut environ 0,7390851332

4°/ L’entourloupe :

Procédure	Exemple	Explications
Le spectateur choisit un nombre à 9 chiffres de son choix sur la calculatrice.	654189327	Soit x le nombre de départ.
Il l’élève au carré.	654189327²	X²
Il soustrait à ce résultat, le produit du nombre de départ +2 et de ce nombre -2.	654189327²-654189325×654189329 = 0	x²– (x+2)(x-2) = x² – (x² – 2²) = x² – x² + 4 = 4 L’affichage de la calculatrice est limité à 9 caractères après la virgule. Voilà pourquoi elle se trompe.
Le magicien prédit à chaque fois que le résultat affiché sera 0 alors que la réponse devrait être 4 !!! Il faut effectuer le travail à la main avant de le faire à la machine pour démontrer ses limites.

V°/ Géométrie :

1°/ Constellations :

Demander de placer entre 5 et 20 points au hasard sur la feuille et de tracer autant de segments rejoignant ces points en respectant deux règles :

→ chaque point doit être relié à au moins un segment, donc les points isolés sont interdits.

→ les segments tracés ne doivent pas se croiser

Le magicien demande seulement 2 éléments au spectateur sur son dessin :

→ le nombre de points

→ le nombre de polygones différents que l’on peut colorier (le nombre de figure fermée).

Le magicien annonce alors sans avoir vu la figure le nombre de segments tracés par le spectateur sur sa constellation !

Explications :

Il y a 11 sommets S, 3 polygone F et 13 segments A.

D’après le Théorème de DESCARTES-EULER : S + F = A + 1

Donc : A = S + F – 1 = 11 + 3 – 1 = 13

2°/ La flèche qui tourne : https://www.youtube.com/watch?v=K_r1Harv6XA

Fabriquer cet octogone dans un carton épais.

Si on met ses doigts en I et E et que l’on fait faire un tour complet à l’octogone, les 2 flèches seront dans le même sens.

Si on met ses doigts en G et C et que l’on fait faire un tour complet à l’octogone, les 2 flèches seront dans le sens inverse.

Pour la mise en scène, il faut effectuer la 1^ière manipulation puis secouer l’octogone pour simuler un quelconque effet magique, et le prendre avec l’autre main pour cacher le changement de position des doigts.

Recto

Verso

Explications :

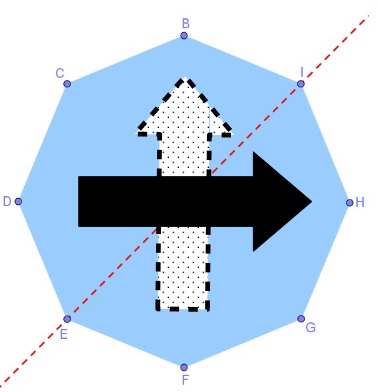
(IE) est l’axe de symétrie des 2 flèches.

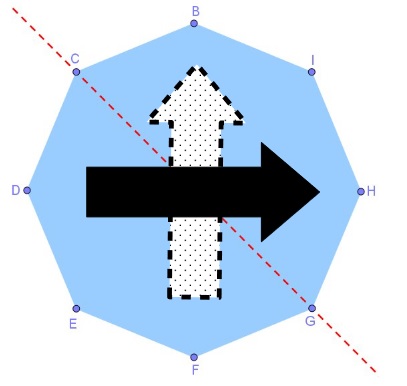
(CG) est l’axe de symétrie des 2 flèches inversée.

VI°/ Tour de cartes :

1°/ Formidable :

Procédure version 01	Exemple
Demander à un spectateur de choisir entre 10 et 19 cartes dans un jeu de plus de 20 cartes. Soit dans l’ordre soit complétement au hasard.	N = 17 cartes
Le spectateur fait la somme S des chiffres du nombre choisi.	S = 1 + 7 = 8
De regarder dans le paquet de N cartes, celle située à cette position face visible.	La 8ème carte.
De remettre la carte à sa place et de replacer ce paquet sur le reste du jeu.
Prenez alors l’ensemble du jeu, faces cachées, et jetez les cartes au fur et à mesure que vous épelez : « F-O-R-M-I-D-A-B-L-E ».	« Formidable » comporte 10 lettres.

Explication :

N	10	11	12	13	14	15	16	17	18	19
S	1	2	3	4	5	6	7	8	9	10
Différence	9	9	9	9	9	9	9	9	9	9

La différence vaut toujours 9 donc en retournant le jeu, faces cachées, la S-ème carte se retrouve toujours en 10ème position soit sur le lettre E du mot « FORMIDABLE ».

Procédure version 02	Exemple
Demander à un spectateur de choisir entre 20 et 29 cartes dans un jeu de plus de 20 cartes. Soit dans l’ordre soit complétement au hasard.	N = 23 cartes
Le spectateur fait la somme S des chiffres du nombre choisi.	S = 2 + 3 = 5
De regarder dans le paquet de N cartes, celle située à cette position face visible.	La 5ème carte.
De remettre la carte à sa place et de replacer ce paquet sur le reste du jeu.
Prenez alors l’ensemble du jeu, faces cachées, et jetez les cartes au fur et à mesure que vous épelez : « V-O-I-L-A L-A C-A-R-T-E C-H-O-I-S-I-E ».	« Voilà la carte choisie » comporte 19 lettres.

Explication :

N	20	21	22	23	24	25	26	27	28	29
S	2	3	4	5	6	7	8	9	10	11
Différence	18	18	18	18	18	18	18	18	18	18

La différence vaut toujours 18 donc en retournant le jeu, faces cachées, la S-ème carte se retrouve toujours en 19ème position soit sur le lettre E de la phrase « V-O-I-L-A L-A C-A-R-T-E C-H-O-I-S-I-E ».

2°/ Lucky 13 :

Procédure	Exemple
Prenez un jeu de 52 cartes (sans les jokers) et ranger-les en 4 colonnes en partant des dames et en allant vers l’as, dans l’ordre (les couleurs n’ont aucunes importance). Demander à un spectateur d’enlever autan de cartes qu’il le désire dans les 4 tas, en laissant au moins la dame.
Le spectateur enlève une colonne de carte qu’il ajoute aux cartes restantes.	Il enlève la 4ième colonne.
Dans ce tas de cartes il enlève 13 cartes car 13 porte bonheur.
Le magicien annonce alors que le nombre de cartes restantes dans les mains du spectateur est la somme des dernières cartes visibles sur chaque paquet.	4 + 7 + 10 = 21 Il reste 21 cartes.

Explication :

Chaque colonne peut contenir au maximum 12 cartes (dame, valet,10, 9, 8, 7, 6, 5, 4, 3, 2, as). Si on note C1, C2, C3, C4 le nombre de carte qui reste par colonne (dans l’exemple : C1=4, C2=7, C3=10 et C4=8), alors le nombre de cartes de chaque paquet est :

Paquet n°	1	2	3	4
Nb de cartes	12-C1+1	12-C2+1	12-C3+1	12-C4+1
Nb de cartes restantes	C1-1	C2-1	C3-1	C4-1	+ 4 rois
Total	12	12	12	12	4×12 + 4 = 52

Le spectateur choisit 3 paquets au hasard. Pour la preuve, prenons les trois premiers (cela ne change en rien le raisonnement). Il reste donc :

C1-1 + C2-1 + C3-1 + 4 + 12 = C1 + C2 + C3 + 13 cartes dans le paquet donné au spectateur (4 rois et les 12 cartes de la 4ième colonne).

En enlevant 13 cartes, il reste C1+C2+C3 cartes au spectateur soit la somme des trois paquets choisis par ce dernier.

3°/ Le décompte :

Procédure	Exemple
Prenez un jeu de 52 cartes (sans les jokers) que l’on mélange. On prend les 9 première carte du jeu sans montrer au spectateur qu’on est en train de les compter.
Le spectateur tire une de ces 9 cartes au hasard et la cache au magicien. Il la remet face cachée sur la pile des 8 cartes restantes.
Les 43 autres cartes sont placées par le magicien au-dessus des 9 cartes. Le magicien fait ensuite 4 piles de cartes avec la règle suivante : On décompte de 10 à 1 pour chaque pile en s’arrêtant si la carte obtenue est égale au nombre cité par le magicien. S’il n’y a aucune carte qui coïncide avec l’énumération, on rajoute une carte face cachée sur la pile.	Ici, pour la 2ième pile, on a dit 10 puis 9 pour poser le 8 de cœur.
Une fois les 4 piles effectuées, on fait la somme N des cartes visibles. Dans les cartes restantes, la N-ème carte est la carte du spectateur !	8 + 4 = 12 donc la 12ième carte est celle recherchée.

Explication :

Pile 1	Pile 2	Pile 3	Pile 4	Somme
10 + 1 = 11 cartes	10, 9, … et 4 = 7 cartes	10, 9 et 8 = 3 cartes	10 + 1 = 11 cartes	11 + 7 + 3 + 11 = 32 cartes
52-11 = 41 cartes restantes	34 cartes restantes	31 cartes restantes	20 cartes restantes

20 cartes – (8+4) = 12ième carte

La carte étant à la 9ième position en partant du fond : 8 cartes au fond puis la carte recherchée puis 11 cartes = 20 cartes

4°/ La matrice :

Procédure	Exemple
Prendre 12 cartes et disposer-les en 3 lignes de 4 cartes (a1, a2, a3, a4, b2… c4). Demander à un spectateur de choisir une carte et de vous désigner la ligne qui la contient : ligne b. Relever les cartes en commençant par a1 que l’on met face visible sous a2 …. jusqu’à c4.	Ligne b
Retourner le paquet face cachée et disposer-les en 3 colonnes de 4 cartes (a1, b1, c1, d1, a2 … c4). Redemander dans quelle ligne se trouve la carte : ligne c	Ligne c
Il faut convertir la 1ière ligne b en colonne 2. La carte sera à l’intersection de la ligne c et de la colonne 2.

Il sera plus spectaculaire de prendre 30 cartes et de commencer par étaler 5 lignes de 6 cartes puis 6 colonnes de 5 cartes.

Explication :

Tout repose sur la notion de matrice. la carte qui était b3 (2ième ligne – 3ième colonne) se retrouve ensuite en c2 (3ième ligne – 2ième colonne).

5°/ Un tour de carte simple et impressionnant :

Disposez 27 cartes réparties en 3 colonnes de 9 cartes.
Demandez à un spectateur de choisir une carte et de vous désigner la colonne dans laquelle elle se trouve.
Rassemblez les cartes de chaque colonne et prenant soin de mettre celle qui contient la carte choisie, au milieu des 2 autres.
Recommencez l’opération 2 fois de plus.
Après avoir rassemblez une dernière fois toutes les cartes, posez les cartes une à une devant vous. La 14ième sera la carte choisit par le spectateur.

L’explication tient dans le fait que le nombre de colonne doit être un diviseur du nombre total de carte. Plus exactement on distribue 3 cartes sur 3 colonnes 3 fois : 3 x 3 x 3 = 27 cartes.


Disposons les 27 cartes dans un ordre précis pour repérer le cheminement des cartes.	A la seconde distribution, on dispose en premier et dans l’ordre, d’abord les cartes de la 1ière colonne puis celle de la 2ième et enfin celles de la 3ième.	A la troisième distribution, les cartes de la colonne du milieu de la distribution précédente contenant la carte recherchée, se retrouve au centre (carte de 2, 5 et 8).

Petites variantes avec un autre nombre de carte.

Nombre de cartes	Disposition	Nombre de redistribution, sans compter la première mise en place	Position de la colonne contenant la carte recherchée	Position de la carte recherchée
32	4 colonnes de 8 cartes	2 (2×4 = 8)	dernière	32ième
25	5 colonnes de 5 cartes	1 (5×1 = 5)	3ième	13ième
50	5 colonnes de 10 cartes	2 (2×5 = 10)	3ième	25ième

6°/ Carte et combinatoire :

C’est un tour automatique donc impossible de le rater pour le magicien qui propose à un spectateur de mélanger un jeu de 52 cartes, sans les jokers.

1°/ Le magicien se retourne pour ne rien voir, et explique au spectateur qu’il doit poser une carte sur la table, face visible, et énoncer dans sa tête toutes les cartes qui la sépare du roi, en posant une carte dessus à chaque fois. Ex : si un 7 est retourné, il dit 8, 9, 10, valet, dame, roi et complète avec donc avec 6 cartes par dessus le 7.
2°/ Le spectateur répète cette manipulation 6 fois en tout. Il obtient 6 paquets de cartes et un paquet de cartes restantes.
3°/ Le spectateur choisit de retourner 3 des 6 paquets. Les autres paquets sont remis avec les autres cartes restantes. Il peut même les mélanger.
4°/ Le spectateur retourne la 1ère carte de 2 paquets de son choix.
5°/ Le magicien va deviner la 1ère carte du 3ème paquet sans l’avoir vu !
Avec le paquet restant, cartes non visibles, il enlève 10 cartes puis le nombre de points correspondant à la valeur des deux cartes des 2 paquets retournés par le spectateur.Le nombre de cartes restantes correspond à la carte du 3ème paquet.Rem : Valet = 10 points; Dame = 11 points et Roi = 12 points

Explications :

Notons i, j et k les 3 valeurs des premières cartes retournées des 3 paquets. Raisonnons sur le paquet i :
Si on continue la famille à partir de i jusqu’au roi, on compte de i+1 à 13 et le paquet contient 13 – i + 1 = 14 – i cartes.
Ex : le 1er paquet du déroulement du tour contenait 7 cartes car la 1ère carte était un 7 soit 14-7=7 cartes.
Il en est de même pour les 2 autres paquets j et k. Le magicien a donc en tout : 14-i + 14-j + 14-k = 42 – (i + j + k ) cartes dans les 3 paquets
Imaginons que le spectateur choisisse de retourner les paquets j et k. Les deux cartes retournées sont donc de valeur j et k et le magicien doit deviner la carte de valeur i !
Notons n le nombre de cartes restantes. On a l’égalité : 52 = n + 42 – (i + j + k ) soit 10 = n – (i + j + k)
donc i = n – 10 – ( j + k ) on enlève 10 cartes et la somme j + k.

7°/ Les 3 cartes :

C’est un tour automatique donc impossible de le rater pour le magicien qui propose à un spectateur de mélanger un jeu de 52 cartes, sans les jokers.

1°/ Le spectateur choisit 3 cartes au hasard, qu’il doit mémoriser et poser devant lui face cachée.
2°/ Le magicien reprend le paquet restant et constitue un paquet de 10 cartes, puis 2 de 15 et enfin un dernier de 9, le plus discrètement possible en expliquant par exemple qu’il partage à peu-près équitablement en 4 tas.
3°/ Le spectateur choisit une de ses 3 cartes au hasard et la pose, face cachée, sur le premier tas de 10 cartes, puis il prend un nombre quelconque de cartes du 1ier tas de 15 qu’il pose dessus pour cacher sa 1ière carte. Il refait de même avec une de ses 2 cartes restantes qu’il pose sur le 2ième tas et qu’il recouvre avec quelques cartes du 2ième tas de 15.
4°/ Le magicien récupère les cartes en empilant le 4ième tas sur le 3ième, puis sur le 2ième et enfin sur le 1ier.
5°/ Le magicien pose la 1ière carte de son paquet devant le spectateur face visible puis la suivante devant lui, face cachée, et ainsi de suite. Le spectateur doit arrêter le magicien lorsqu’il voit l’une de ses cartes, ce qui n’arrivera pas !!!
6°/ Le magicien récupère les cartes faces cachées et refait de même en commençant par poser une carte visible. Toujours pas de carte choisie.
7°/ Le magicien refait de même une 3ième fois mais cette fois-ci sa 1ière carte sera face cachée.
8°/ Et enfin une 4ième fois en commençant par une face visible.
9°/ Il va rester 3 cartes qui seront celles choisies par le spectateur.

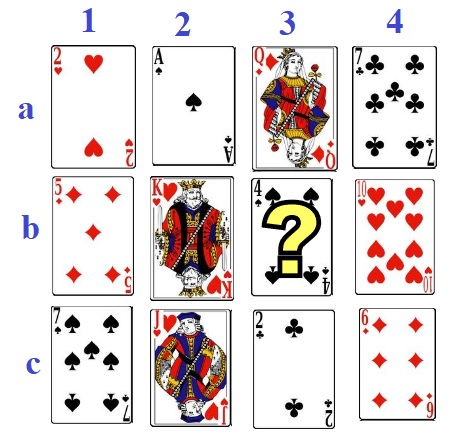
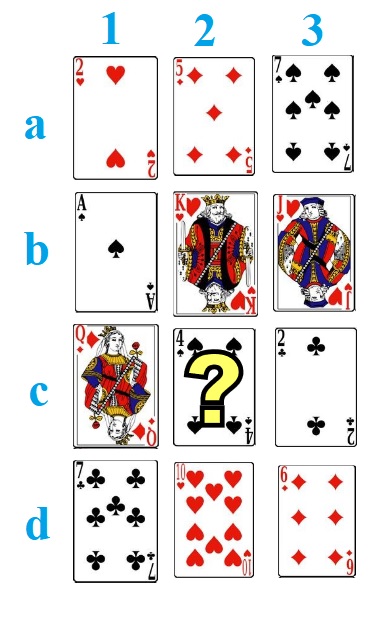
8°/ La carte retrouvée :

Procédure	Exemple	Explications
Demandez à un spectateur d’écrire en cachette un nombre de quatre chiffres.	4327	1000a + 100b + 10c + d
Calculer la somme de ces quatre chiffre.	4 + 3 + 2 + 7 = 16	a + b + c + d
Soustraire au nombre de départ la somme trouvé.	4327 – 16 = 4509	1000a + 100b + 10c + d – (a + b + c + d) = 999a + 99b + 9c = 9 (111a + 11b + c) Le résultat obtenu est donc un multiple de 9, la somme de ses chiffres est donc aussi un multiple de 9.
De sortir du jeu de 52 cartes 4 cartes correspondant aux chiffres du résultat obtenu, mais de 4 couleurs différentes.	4509 : 4 de cœur, 5 de carreau, 10 de trèfle et 9 de pique (pour un 0, prendre un 10).
Cacher une de ces 4 cartes et de montrer les trois autres.	5 de carreau	Le complément à 9 de 4 + 0 + 9 = 13 → 1 + 3 = 4 9 – 4 = 5 La carte sera le 5 de la couleur non visible.
Annoncez alors presque aussitôt au spectateur la carte cachée !!!

9°/ Le tour inexplicable, expliqué : d’autres tour expliqués :https://www.youtube.com/watch?v=CCbX7Ducxfs&list=PLyw0heJPXGZ6R7IQUO9Zf7FXaocZiv5G8&ab_channel=Abracademie

VII°/ Pliage, construction et tour de magie :

1°/ La quadrature des cercles :

Un titre historique alléchant pour ce tour de magie basé sur un des trois grands problèmes grecs issus de l’Antiquité ! Est-il possible de construire à la règle non graduée et au compas :
• un cube dont le volume est le double d’un cube donné → la duplication du cube
• un angle en trois angles égaux → la trisection de l’angle
• un carré de même aire qu’un cercle donnée → la quadrature du cercle
Depuis Galois et Wantzel, on sait que ces trois problèmes sont impossibles !

Le tour redonne l’illusion de transformer deux cercles en un carré. Comment changer des formes arrondis en une figure à angles droits ?

Découper 2 anneaux de papier.

Les coller perpendiculairement.

Découper l’anneau horizontal sur toute sa longueur.

On obtient une sorte de menotte. Découper la bande, qui correspond au second anneau, lui aussi sur toute sa longueur.

Miracle, on a construit un carré avec 2 anneaux sans aucun angle droit.

2°/ La gravité biaisée :

Jouons avec la gravité.

Voici un oiseau que j’utilise en classe pour illustrer le centre de gravité.

On pourrait croire que le centre de gravité se trouve au niveau du ventre, mais l’oiseau est creux et donc très léger, et deux plombs sont situés au bout des ailles. Le centre de gravité s’en trouve déplacer sur le bec.

Voici un petit objet a construire dans du bois ou un carton épais et qui permet de faire tenir pratiquement n’importe quoi sur le bout de son doigt.

Une vidéo explicative : https://youtu.be/9PrqXRTmVuk?list=PLtHz3o7aW7BBvgx6cUkPA08yYpRJBZilY

Un fichier pour télécharger un modèle.

3°/ Bracelets de Möbius :

Construire un anneau de papier. En le découpant dans le sens de la longueur, peut-on :

– Doubler la longueur de l’anneau.

– Construire 2 anneaux entrelacés.

Si on construit cetun anneau de papier.

On obtient 2 anneaux mais ils ont la même taille que au début.

Il faut tourner d’un demi-tour la bande de papier avant de la coller. On a construit un anneau de Möbius.

Découpant dans le sens de la longueur.

On obtient un seul anneau de longueur double.

Si on faut tourner d’un tour complet la bande de papier avant de la coller.

Cette fois on a construit 2 anneaux entrelacés.

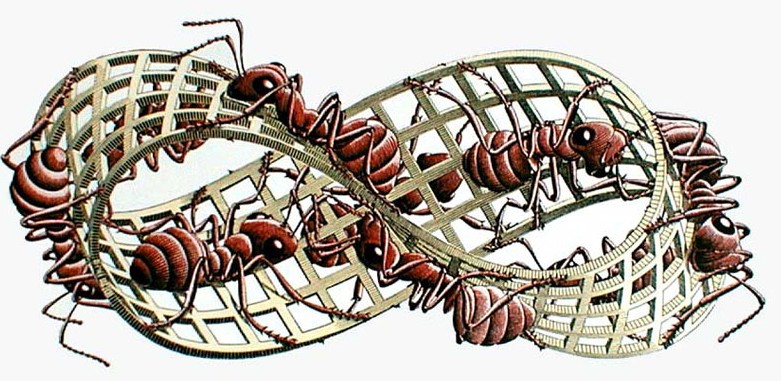
Ruban de Möbius représenté par Escher

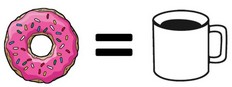
En topologie, un beignet et une tasse à café avec son anse sont deux objets similaires, car il s’agit d’un objet avec un trou.

D’autre découpages :

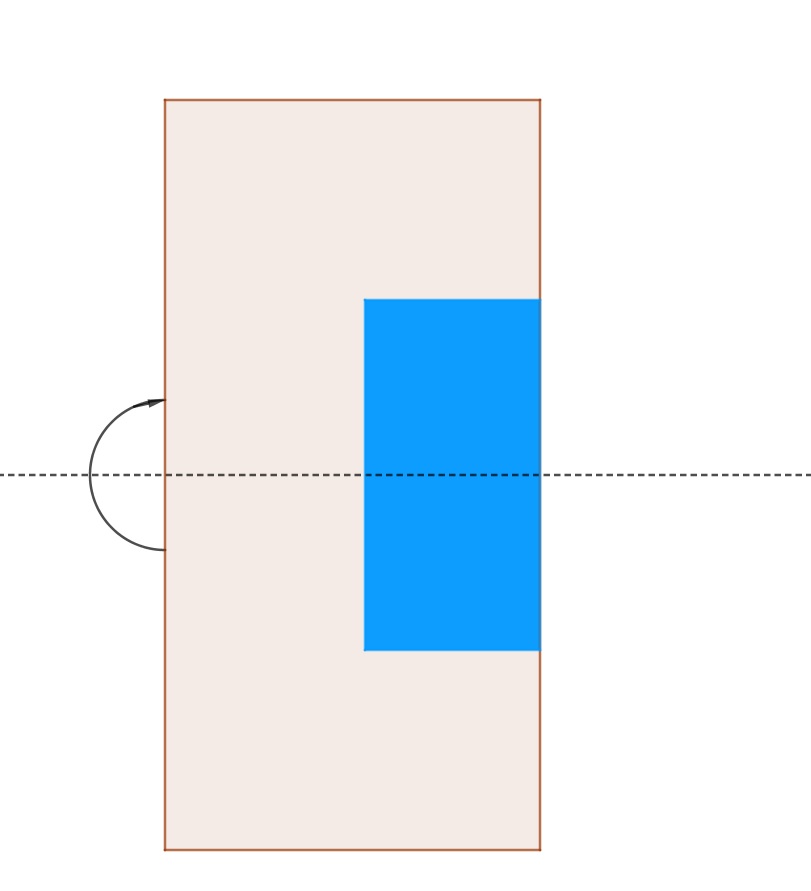
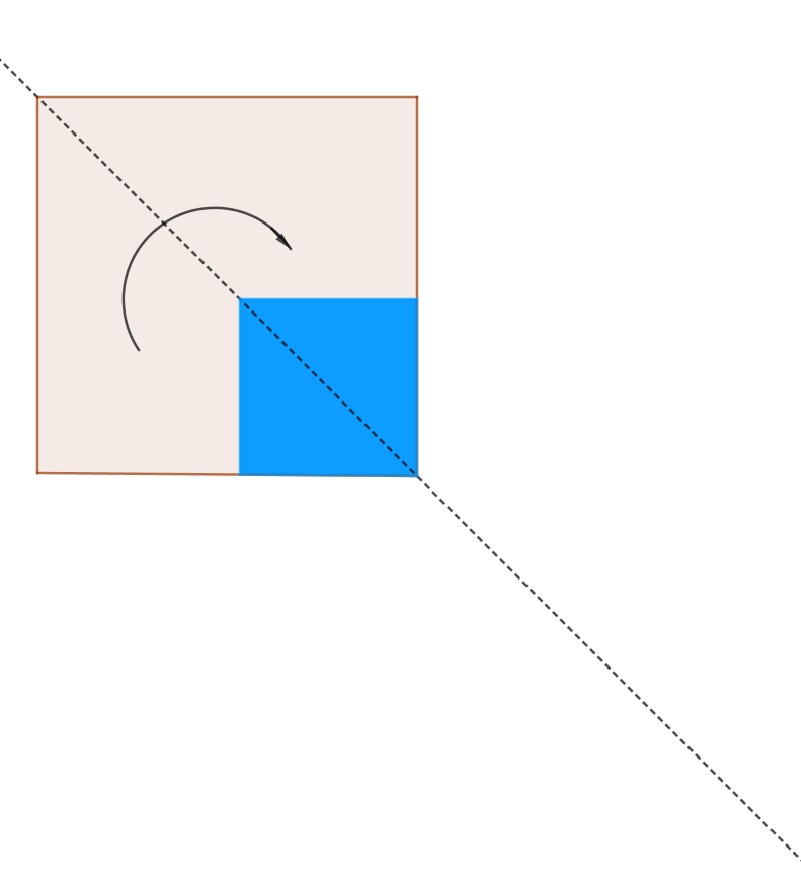
4°/ Avec 1 seul coup de ciseau :

Peut-on découper un carré dans une feuille de papier en un seul coup de ciseau ?


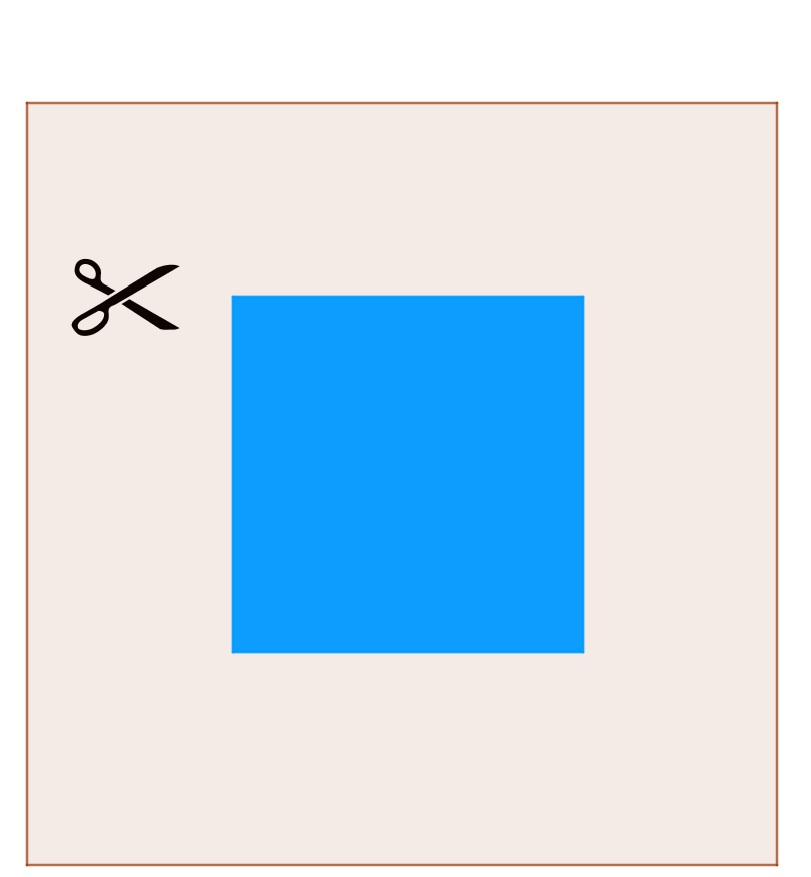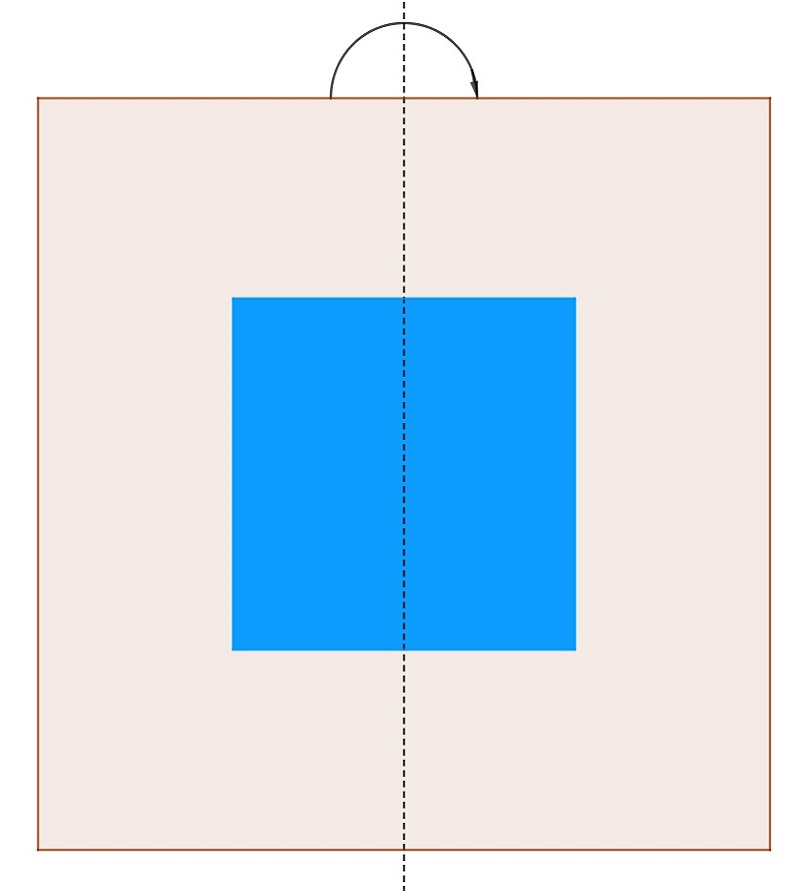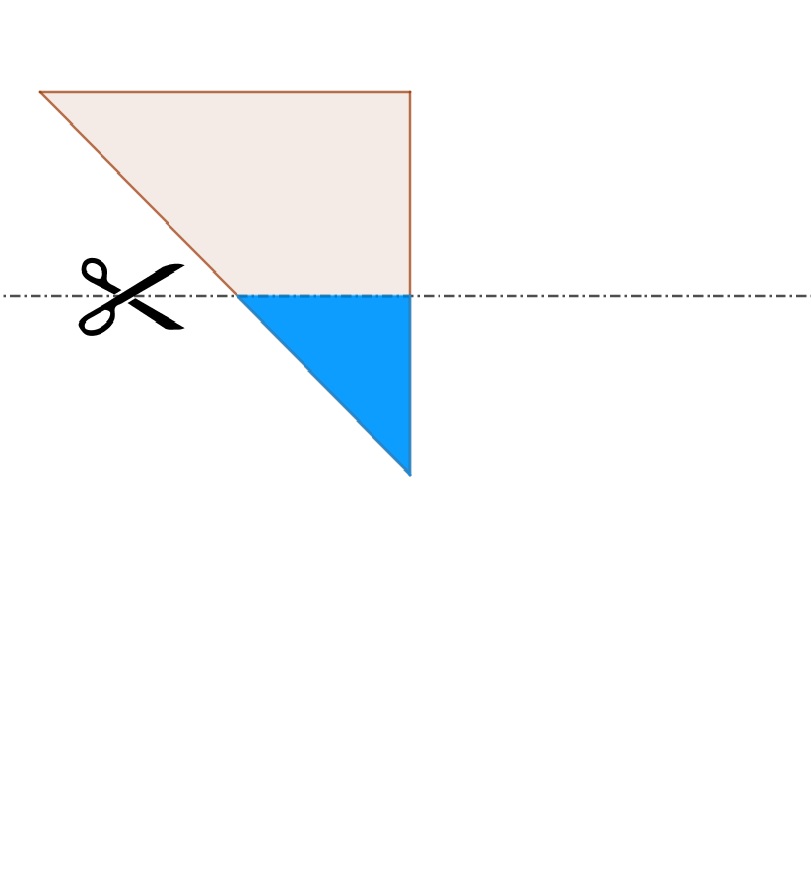Apparemment il faut 4 coups de ciseaux.	En pliant la feuille en deux, il reste 3 coups coups de ciseaux.	En pliant encore la feuille en deux, il reste encore 2 coups coups de ciseaux.	Et repliant selon la diagonale, un seul coup de ciseaux suffira.	On remarque que l’on plie la feuille selon les axes de symétrie.

Voici d’autre réalisations.

Un triangle équilatéral

Une étoile

Une vidéo explicative.

On peut ainsi fabriquer n’importe quel polygone après des pliages selon les axes de symétrie. C’est le théorème du « Cut and Fold ».

Couper en un seul coup de ciseaux :

Théorème du Cut & Fold

by Erik Demaine, Martin Demaine, and Katie Steckles, 2016

Entrer le texte à construire :

Ne pas afficher le texte

Créer les motifs

Étapes de pliage

Lettre découpée

Grille

Lignes de pliage (vert dans un sens;bleu dans l’autre)

– Voici des PDF imprimables pour toutes les lettres et les nombres.
– D’autres polices mathématiques et des puzzles .Site source.
– Le site source.

5°/ Silk : dessiner de magnifique dessin basés sur les transformation du plan.

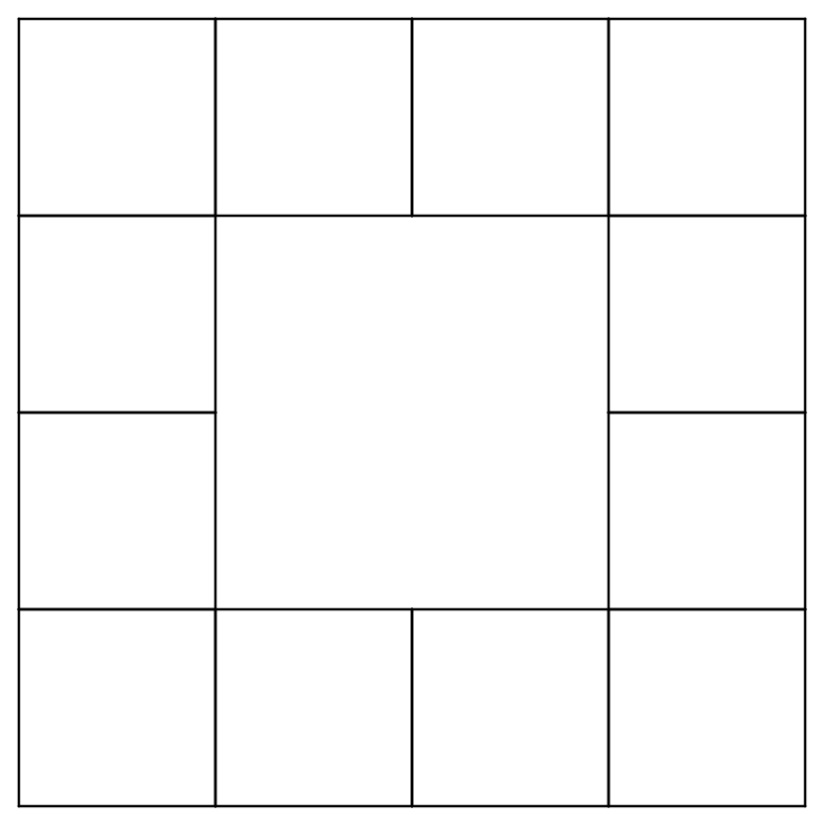
6°/ Hexatétraflexagone :

Le magicien montre un carré aux spectateurs recto-verso. Puis après manipulation, il fait apparaître 1, 2, 3 et 4 nouvelles faces ! Effet garanti

Le patron de l’Hexatétraflexagone.

Une variante pour réaliser une carte de vœux ou d’anniversaire.

D’autres constructions à réaliser : http://trabucaire.free.fr/index.php/maths-pour-travailler/xxxi-la-4ieme-dimension/

7°/ La légende de Didon :

Didon, princesse phénicienne en exil, est à l’origine de la fondation de Carthage (en Tunisie actuelle). Voulant échappé à la tyrannie de son frère qui assassina son mari, elle trouva refuge et demanda l’asile aux autochtones appelés les Gétules (peuple berbère).
Ces derniers lui offrirent comme territoire tout ce qui pouvait être entouré par une peau de bœuf. Astucieuse et réfléchie, Didon découpa la peau en fines lanières qui, assemblées mesuraient 4 km ! Le territoire ainsi encerclé sur la colline de Biras (qui signifie bœuf) donna naissance à la ville de Carthage en 814 avant J.-C

Le magicien demande aux spectateurs de faire un trou à l’intérieur de la feuille pour qu’il puisse passer à travers. C’est impossible, n’est ce pas ?

Pour cela, découper une feuille A4 de la façon ci-contre.

8°/ Évasion ou l’éloge de la topologie :

La topologie est une branche fascinante des mathématiques qui décrit les propriétés d’un objet qui restent inchangées sous des déformations « douces » continues. En fait, de nombreux puzzles 3D sont basés sur des principes topologiques et comprendre certains principes très fondamentaux peut vous aider à analyser si un puzzle est possible ou non.

Ici nous allons créer des tours de magie qui vont nous permettre de nous évader façon Houdini.

9°/ Synchronisation des bras :

– Tendez vos 2 bras horizontalement.
– Tracer un cercle avec votre bras droit.
– Tracer un carré avec votre bras gauche.
– Tracer un cercle avec votre bras droit et un carré avec votre bras gauche.

Cela devient beaucoup plus compliqué à faire, car l’hémisphère droit de notre cerveau commande le bras gauche et le gauche le bras droit. Il nous est très difficile de contrôler nos deux hémisphère en même temps !!

10°/ 50 mots :

Êtes-vous capable de donner 50 mots ne contenant pas la lettre L en 20 secondes ?

Astuce : 20 secondes c’est vraiment très court, et le chalenge est impossible, sauf avec un peu de réflexion. Il suffit de réciter les nombres de zéro à quarante-neuf.

Référence : http://www.pearltrees.com/labo_m_toucy/mathemagie/id19427363 : Le dernier fait : #201