Enigmes

Voici les toutes les énigmes avec leurs solutions.
Cliquez sur la flèche en haut à droite de la chaque page pour les ouvrir dans Microsoft Office Online. Vous pouvez aussi les télécharger au format Word.

A la 4ième page, il y a des liens pour les télécharger au format Word.

Énigmes avec leurs solutions de 001 à 199

Download File

.400°/ Frères et sœurs :

Un garçon affirme : « j’ai autant de frères que de sœurs ». Sa sœur répond : « j’ai deux fois plus de frères que de sœurs ».
Combien y a-t-il d’enfants dans cette famille ?

.401°/ Le cuisson des steaks :

Mon grill ne peut contenir que 2 steaks à la fois.
Pour cuire une pièce de viande, il faut 5 minutes de chaque côté.
Quelle la durée minimale pour cuire 3 steaks ?

.402°/ Une question de Français :

Voici une phrase : J’ai 192 poule.
Poule ne prend pas de ‘s’ pourquoi ?

.403°/ Un père et son fils :

Quand on additionne l’année de naissance d’un père, celle de son fils, l’âge du père et l’âge du fils, qu’obtient-on ?

.404°/ Les petits cailloux :

Combien de cailloux font 671 pierres et 71 cailloux ?

.405°/ La rivière :

Il y a 4 personnes d’un côté de la rivière et une barque.
La barque contient soit 1 soit 2 personnes. Elle se déplace à la vitesse de celui qui rame le plus lentement.

Parmi les 4 personnes : il y a monsieur Huit qui met 8 minutes à traverser, monsieur Quatre qui met 4 minutes à traverser, monsieur Deux qui met 2 minutes à traverser, et enfin monsieur Un qui met 1 minute à traverser.

Comment doit-on organiser l’ordre des passages pour que tout le monde soit sur l’autre rive en un minimum de temps ? Quel est ce temps minimum ?

(Attention à ne pas oublier le temps pour revenir à chaque retour).

.406°/ Les 2 paysans :

Deux paysans se sont rendus à la foire avec 110 bêtes au total.
Après avoir vendu tout leur cheptel, ils constatent qu’ils ont gagné exactement la même somme. L’un d’eux remarquent que s’ils avaient interverti leurs prix, le premier aurait gagné 3300 € de plus que l’autre, qui aurait eu 7500 €.
Combien chacun a-t-il gagné ?

.407°/ Rayon de la terre avec le Théorème de Pythagore et une équation du second degré :

2 montagnes, hautes respectivement de BS’ = 2 km et de AS = 1,2 km, et dont les sommets sont espacés de 36 km, sont telles que si on se place sur le sommet de la plus haute, le sommet de l’autre est au niveau de l’horizon.
Que vaut le rayon OH de la Terre ?

.408°/ Papa, c’est loin l’horizon ?

Je suis juste au bord de l’eau. La mer est calme et mes yeux sont à CD = 1,65 m du sol. A quelle distance se trouve l’horizon CB ?
(Rayon de la Terre : AD = environ 6380 km)

.409°/ Un problème de calcul :

Voilà un problème qui a l’air tout simple :
A l’aide des quatre opérations élémentaires (éventuellement des parenthèses) et en utilisant une seule fois les nombres 1, 5, 6 et 7, trouver 21

.410°/ A la maternelle :

Une maîtresse de grande section de maternelle demande à ses élèves de couper des bandes de 2cm par 10cm.
Pour cela, elle leur donne une feuille carrée de 10×10 cm. En moyenne un enfant de cette classe met 20 secondes pour couper une bande.
Combien de temps mettra en moyenne un enfant pour couper entièrement sa feuille en bandes ?

.411°/ Le télésiège :

Les sièges d’un télésiège sont régulièrement espacés et numérotés dans l’ordre à partir de 1.
Lorsque la place 13 croise la place 25 alors le siège 46 croise le 112.
Quel est le nombre de sièges au total ?

.412°/ Les livres :

Il y a plusieurs livres sur une étagère.
Si un livre est le cinquième en partant de la gauche et le cinquième en partant de la droite, combien y a t-il de livres sur cette étagère ?

.413°/ Une virgule qui coûte cher :

Un peu étourdi, Simon a oublié d’écrire la virgule sur son chèque lorsqu’il a payé l’essence pour son scooter.
Une bêtise qui lui coûte cher : 1826,55 € de trop. Son compte bancaire est dans le rouge.
Quelle somme aurait-il dû écrire sur son chèque ?

.414°/ J’ai beaucoup d’amis :

Imaginons que vous ayez énormément d’amis (un nombre infini). Le premier vient vous voir et vous demande 1/2 coupe de champagne. Le deuxième vous demande 1/4 de coupe du champagne. Le troisième demande 1/8 etc…

Combien de coupes de champagne devez-vous prévoir pour satisfaire tous vos amis ?

.415°/ Attention piège :

Un grand père, prof de Maths à la retraite, demande à son petit-fils :
Grand père : « Quelle est la moitié de 2 + 2 ? »
Petit fils : « Heu ! c’est 2. »
Grand père : « Et non. Mais que t’apprend-on à l’école ? »
Quelle était la bonne réponse ?

.416°/ Interférences dans un avion :

A quelques minutes du décollage, une hôtesse de l’air constate des interférences. Elle demande alors aux passagers :
“Qui a son ordinateur allumé ?” Quinze mains se lèvent.
“Qui a son téléphone allumé ?” Treize mains se lèvent.
“Qui a les deux allumés ?” Sept personnes se manifestent.
“Qui n’a ni ordinateur ni téléphone allumé ?” Neuf personnes répondent.
Combien y a t-il de passagers dans l’avion sans compter le personnel navigant ?

.417°/ Quel est le nombre ?

Quel est le nombre entier à deux chiffres qui, divisé par la somme de ses deux chiffres, donne pour résultat la somme de ses deux chiffres ?

.418°/ Poisson, palmier et pagaie :

.419°/ Les cierges :

Frère Luc est l’intendant d’une abbaye.
Très économe, il réutilise des bouts de cierges usagés pour en faire des nouveaux. Il est capable de reconstituer un cierge à partir de trois bouts de cierges qu’il fait fondre.
Combien pourra t-il reconstituer de cierges au total avec les 9 bouts de cierges qu’il a récupéré ce matin dans l’abbatiale ?

.420°/ L’âge des filles :

Un facteur apporte une lettre à un homme père de 3 filles.
Il demande l’âge des filles.
Le père lui dit que le produit des âges vaut 36 et que la somme des âges est égale au numéro de la maison d’en face.
Le facteur se retourne, regarde le numéro et dit :
« Cela ne me suffit pas. »
Le père rajoute alors :
« La plus jeune est blonde. »

.421°/ Énigme : Je trouve le carré d’arrivé après 4 mouvements consécutifs.

1°/ Choisissez un carré bleu de cette grille.
2°/ Allez à gauche ou à droite jusqu’au carré rouge le plus proche.
3°/ Montez ou descendez jusqu’au carré bleu le plus proche.
4°/ Allez en diagonale jusqu’au carré rouge le plus proche.
5°/ Descendez ou allez à droite jusqu’au carré bleu le plus proche.

.422°/ Les 3 portes :

Vous devez entrer dans l’une de ces 3 pièces.
Dans la première il y a des assassins armés jusqu’aux dents, dans la seconde il y a lion féroce qui n’a pas manger depuis trois mois et dans la dernière il y a un incendie qui fait rage. Vous choisissez laquelle ?

.423°/ Le bus :

Vous conduisez un bus qui transporte 10 passagers.
Au 1^ier arrêt 3 personnes descendent et 4 montent.
Au 2ième arrêt 4 personnes descendent et 2 montent.
Au 3ième arrêt 10 personnes descendent et 5 montent.
Au 4ième arrêt 8 personnes descendent et 2 montent.
Au 5ième arrêt 9 personnes descendent et 5 montent.
Combien y a-il de passagers dans le bus et quel est l’âge du conducteur.

.424°/ Es-tu majeur ?

J’ai trois fois l’âge que vous aviez quand j’avais l’âge que vous avez. Quand vous aurez l’âge que j’ai, nous aurons ensemble 56 ans. Êtes-vous majeur ?

.425°/ Quel est mon âge ?

Quand mon père a eu 31 ans, j’en avais 8. Aujourd’hui, il est deux fois plus âgé que moi. Quels sont nos âges ?

.426°/ Le lion de bronze :

Je suis un lion de bronze ; deux jets jaillissent de mes yeux, un autre de ma gueule, un autre de mon pied. En deux jours, mon oeil droit remplit le bassin, mon œil gauche en trois, et mon pied en quatre jours. Pour le remplir, six heures suffisent au jet d’eau de ma gueule. Si tous les jets, et de mes yeux et de ma gueule et de mon pied, coulent à la fois, en combien d’heures le bassin sera-t-il rempli ?

.427°/ Les pommes Grecques :

Ayant cueilli des pommes, Myrto les partagea entre ses amies : elle en donna le cinquième à Chrysis; le quart à Héro ; le dit-neuvième à Psamathé ; le dixième à Cléopatre ; le vingtième à Parthénopée. Évadné ne reçut que douze pommes ; et pour elle-même elle en garda cent vingt.

Combien de pommes pour chacune ?

.428°/ L’agent mathématicien Mr McGuire :

« Bien le bonjour, Monsieur l’agent – dit Mr McGuire – Pouvez-vous me dire l’heure ? « 
« Mais bien sûr répondit l’agent qui avait une réputation de mathématicien
Ajoutez au quart du temps depuis minuit, la moitié du temps jusqu’à minuit et vous aurez l’heure exacte. »

.429°/ Combien pése le bébé de madame O’Toole ? Un problème de Sam Loyd.

Madame O’Toole qui est très économe, essaye de se peser ainsi que son chien et le bébé avec une seule pièce. Si elle pèse 100 livres de plus que le chien et le bébé réunis, et si le chien pèse 60% de moins que le bébé, combien pèse le petit chérubin ?

.430°/ Le partage des châtaignes. Un problème de Sam Loyd.

Après avoir ramassé 770 châtaignes, les trois petites filles les ont partagées proportionnelement à leurs âges. A chaque fois que Mary pris quatre châtaignes, Nellie en pris trois. A chaque fois que Mary pris six châtaignes, Susie en pris sept. Combien de châtaignes chaque fille a-t-elle obtenu ?

.431°/ Le puzzle du lac : Un problème de Sam Loyd.

Quelle est la surface du lac triangulaire ?

.432°/ Le problème de l’étameur : Un problème de Sam Loyd.

Cet étameur vient de terminer la fabrication de ce récipient à fond plat de 18 cm de profondeur et dont la contenance est de 25 L.   Combien de nos farouches mathématiciens pourront nous indiquer (au dixième de centimètre près) le diamètre du haut de ce récipient sachant qu’il est le double de celui du fond ?

.433°/ Comptez les voix : Un problème de Sam Loyd.

Lors d’un vote, 5 219 bulletins furent déposés dans une urne. Le vainqueur battait ses trois concurrents de respectivement 22, 30 et 73 voix. Cependant, personne ne put déterminer exactement le nombre de voix obtenues par chaque candidat. Pouvez-vous le faire ?

.434°/ Quel est l’âge de Fido ? Un problème de Sam Loyd.

Charley Slowpop était sur le point de faire sa demande en mariage à son amie, lorsque le petit frère de celle- ci et son chien Fido entrèrent dans le salon.
« Tu ne peux pas connaître l’âge d’un chien à son collier, dit l’enfant terrible. Mais il y a cinq ans, ma sœur était cinq fois plus âgée que Fido et à présent, elle est trois fois plus âgée que lui ! »
Charley Slowpop est très curieux de savoir l’âge de Fido. Pouvez-vous l’aider ?

.435°/ Le problème du messager : Un problème de Sam Loyd.

Un problème ancien, que l’on trouve dans de nombreux vieux livres de problèmes, concerne une armée de cinquante kilomètres de long.
Alors que l’armée avance à une vitesse constante, un messager part de l’arrière-garde de l’armée, galope pour aller délivrer un message à l’avant, puis revient à l’arrière garde.
Il arrive à l’arrière garde exactement au moment où l’armée a parcouru cinquante kilomètres.
Quelle est la distance totale parcourue par le messager ?

.436°/ Quel est l’âge de Meritxell ? Un problème de Sam Loyd.

Un fermier, et sa femme ont eu quinze enfants, nés à un an et demi d’intervalle. Meritxell, la plus âgée des enfants prétend être huit fois plus âgée que Jordi, le plus jeune de la couvée.
Quel est l’âge de Mademoiselle Meritxell ?

.437°/ Les trois mendiants : Un problème de Sam Loyd.

Une dame charitable rencontre un pauvre auquel elle donne la moitié de l’argent qu’elle avait dans son porte- monnaie plus 1 €. Le pauvre, qui est membre de l’association des mendiants unifiés, réussit en la remerciant à dessiner à la craie le signe de remerciement de l’association sur ses vêtements, ce qui permit à la dame de mener à bien son œuvre de charité au cours du reste de sa promenade.
Au deuxième solliciteur, elle donna la moitié de ce qui lui restait plus 2 €.
Au troisième, elle donna la moitié de ce qui lui restait plus 3 €.
À présent, il lui reste un seul euro.
Combien avait-elle au début de sa promenade ?

.437°/ Le prix des œufs : Un problème de Sam Loyd.

« J’ai payé douze centimes pour les œufs que j’ai achetés chez l’épicier, mais je lui ai demandé d’en ajouter deux gratuitement parce qu’ils étaient trop petits. J’ai donc payé mes œufs un centime de moins par douzaine.

Combien d’œufs j’ai acheté ?

.438°/ Quel est l’âge de ce garçon ? Un problème de Sam Loyd.

« Quel est l’âge de ce garçon ? » – demanda le contrôleur.
Le banlieusard, flatté de l’intérêt que l’on porte à sa famille, répondit : « Mon fils est cinq fois plus âgé que ma fille, ma femme est cinq fois plus âgée que mon fils, et je suis deux fois plus vieux que ma femme, tandis que ma grand-mère dont l’âge égale à la somme de nous tous, fête aujourd’hui son quatre-vingt-et-unième anniversaire. »
Quel était l’âge de ce garçon ?

.439°/ Le problème du marché : Un problème de Sam Loyd.

Un fermier et son épouse vont au marché échanger leurs poulets pour du bétail au taux de 85 poulets pour un cheval et une vache, 5 chevaux valant exactement autant que 12 vaches.
« John, dit la femme, prenons encore une fois autant de chevaux que nous en avons déjà pris. Nous n’aurons ainsi que 17 chevaux et vaches à nourrir cet hiver.
« Je crois que nous devrions avoir plus de vaches que cela dit John. D’ailleurs, si nous avions 2 fois plus de vaches que jusqu’à maintenant, cela nous ferait 19 vaches et chevaux en tout et nous aurions juste assez de poulets à donner en échange.
Combien les paysans ont-ils apporté de poulets au marché ?

.440°/ Les deux dindes : Un problème de Sam Loyd.

“Ces deux dindes pèsent 20 livres à elles deux “, dit le boucher.
“La plus petite coûte 2 centimes de plus à la livre que la grande.”
Mme Smith a payé 82 centimes pour la petite et Mme Brown 2,96 Francs pour la grande.
Combien pesaient-elles chacune ?

.441°/ Des timbres pour un franc : Un problème de Sam Loyd.

La dame tend un franc à l’employé et dit : « Donnez-moi quelques timbres à deux centimes, dix fois autant de timbres à un centime et le reste en timbres à cinq centimes. » Comment remplir cette commande ?
Soit x le nombre de timbres à deux centimes et y le nombre de timbres à 5 centimes.
Nous devons donc résoudre l’équation : 2x +10x + 5y = 100, sachant que x et y sont des entiers naturels. L’équation équivaut à 12x + 5y = 100.
x et y étant des entiers naturels, la seule solution possible est x = 5 et y = 8.

.442°/ Le poids d’une brique : Un problème de Sam Loyd.

Si une brique est équilibrée par les trois quarts d’une brique et trois quarts d’une livre, combien pèse cette brique ?

.443°/ La division des pommes : Un problème de Sam Loyd.

Huit enfants ont divisé 32 pommes comme suit : Anne a eu une pomme, May 2, Jane 3, et Kate 4. Ned Smith en prit autant que sa sœur, Tom Brown en prit deux fois plus que sa sœur, Bill Jones trois fois plus que sa sœur et Jack Robinson quatre fois plus que sa sœur. Le problème est de trouver le nom de famille des quatre filles.

.444°/ La promenade à bicyclette : Un problème de Sam Loyd.

Tracez la route de Philadelphie à Erié passant une et une seule fois par chacune des villes représentées.

.445°/ Mère et fille commutative :

La mère de votre fille est-elle la fille de votre mère ?

 .446°/ Nombre en lettre :

Quel est le plus petit nombre qui peut s’écrire avec moins de lettres que lui-même ?

.447°/ La suite logique :

Quelle la logique qui permet de passer de 20 à 4 puis à 16 et ainsi de suite jusqu’à 145 et surtout quel le nombre qui manque entre 145 et 20 ?

.447°/ La suite de John Conway :

Voici une suite. Quelle est sa logique, son 6^ième et son 2020^ième termes ?

1
1 1
2 1
1 2 1 1
1 1 1 2 2 1
3 1 2 2 1 1

.448°/ Du triangle obtusangle aux triangles acutangles :

Peut-on découper un triangle obtusangle (ou encore amblygone), c’est-à-dire avec un angle obtus, en plusieurs triangles acutangles, c’est-à-dire sans angles obtus ?

.449°/ Énigme d’Albert Einstein :

Dans un pays imaginaire il y a 5 maisons alignées de 5 couleurs différentes. Dans chaque maison vit une personne de nationalité différente. Chaque personne boit une certaine boisson, supporte une équipe de rugby et élève un animal différent.

On a les indices suivants :

L’Anglais vit dans la maison rouge.
Le Suédois élève des chiens.
Le Danois boit du thé.
La maison verte est juste à gauche de la maison blanche.
Le propriétaire de la maison verte boit du café.
Le supporter de Pau élève des oiseaux.
Le propriétaire de la maison jaune supporte l’ASM.
L’homme qui vit dans la maison du centre boit du lait.
Le Norvégien vit dans la première maison.
L’homme qui supporte Biarritz vit à côté de celui qui élève des chats.
La personne qui élève des chevaux vit à côté du supporter de l’ASM.
Le supporter de Béziers boit de la bière.
L’Allemand supporte l’USAP.
Le Norvégien vit à côté de la maison bleue.
L’homme qui supporte Biarritz a un voisin qui boit de l’eau.

Qui a un poisson ? Quelle est sa nationalité, son équipe, sa boisson et son animal ?

.450°/ Des nombres en pyramides :

Quelle est la somme de tous les nombres de la 20e rangée?

.451°/ Trouver 21 :

Avec les nombres 1, 5, 6 et 7, et les quatre opérations de base il faut trouver 21.

.452°/ Les équations :

Résoudre chaque équation en les complétant par les bons symboles Mathématiques :

1  1  1 = 6 2  2  2 = 6 3  3  3 = 6 4  4  4 = 6 5  5  5 = 6

6  6  6 = 6 7  7  7 = 6 8  8  8 = 6 9  9  9 = 6

.453°/ Question d’heure :

Voici une pendule sans les nombres. Seriez-vous capable de donner l’heure indiquée en sachant que les aiguilles des heures des minutes et des secondes sont bien placées mais de même taille ?

.454°/ Question de triangle :

Le petit triangle central est plus petit que le grand, mais combien de fois ?

.455°/ Picsou :

Picsou a 2 pièces de monnaie qui font en tout 30 centimes. Etant donné que l’une des pièces n’est pas une pièce de 10 centimes, quelle est la valeur de chacune des pièces ?

.456°/ 1111 – 1 :

Combien de fois peut-on soustraire 1 à 1111 ?

.457°/ Les jetons dans le noir :

100 jetons sont disposés sur une table. Chaque jeton possède une face blanche et une face noire indiscernable au touché. On sait que l’on a 25 jetons blancs et donc 75 noirs.

On place tout cela dans le noir et on vous demande de partager ces 100 jetons de telle façon qu’il y ait autant de blanc d’un côté que de l’autre. Comment faire sans ajouter ou enlever de jeton, ou allumer la lumière.

On peut seulement retourner des jetons et les deux tas ne seront pas forcement égaux.

.458°/ 31 oct = 25 dec ?

J’affirme que 31 oct = 25 dec. Comment delà est-il possible ?

. 100°/ Les escargots, le retour :

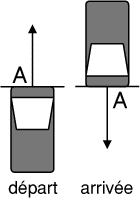
Deux escargots font la course pour escalader un poteau de 15 mètres. A chaque fois que le premier (appelons-le A) monte de 2 mètres il redescend d’un mètre, tout au long de sa progression ; le deuxième par contre (appelons-le B), monte de 4 mètres et redescend de 2 mètres. Ils se déplacent tous les deux à la même vitesse. Cette vitesse est constante, qu’ils montent où qu’ils descendent. Cependant, le second (B) se sentant plus fort que le premier (A), lui accorde un avantage, en le laissant partir avant lui. Ainsi, il attend que son adversaire soit monté et redescendu une fois, pour se lancer dans la course. Sauriez-vous dire lequel arrivera le premier à mi-parcours et qui parviendra au sommet en tête ?

. 101°/ Les maillons des petites chaînes :

J’ai trouvé dans mon garage, 5 petites chaînes de 3 maillons chacune (je garde vraiment n’importe quoi dans ce garage). Je veux fabriquer une seule chaîne de 15 maillons à partir de mes 5 petits bouts. Il faut pour cela que je scie certains maillons puis que je les ressoude après avoir relié plusieurs maillons. Je mets 10 min à scier un maillon (ils sont gros quand même et ma scie est toute rouillée) mais seulement 5 min pour les ressouder.

Comment dois-je faire pour avoir ma grande chaîne le plus rapidement possible ? Combien de temps cela me prendra-t-il ?

. 102°/ Saut d’un seau :

Six seaux sont alignés. Les trois premiers sont emplis d’eau, les trois suivants sont vides. En ne déplaçant qu’un seul seau, faites alterner les seaux vides et les seaux pleins.

. 103°/ Les peintres :

Un homme peut peindre une pièce en quatre heures, tandis que son collègue arrive à peindre cette même pièce en deux heures seulement.

Combien de temps vont-ils mettre pour peindre la pièce, s’ils travaillent ensemble ?

. 104°/ Les faucheurs :

Une équipe de faucheurs avait à faucher deux prés dont l’un était deux fois plus grand que l’autre. Durant une moitié de la journée, l’équipe a fauché une partie du grand pré. Ensuite elle s’est divisée en deux groupes égaux. Les faucheurs de la première équipe sont restés sur le grand pré qu’ils ont fini de faucher vers le soir ; ceux du second ont fauché le deuxième pré également jusqu’au soir, mais il en est resté une parcelle qu’un faucheur a terminé le lendemain en une journée de travail. Combien de faucheurs y avait-il dans l’équipe ?

. 105°/ Un cube et un carré avec si peu d’allumettes ?

Faire un cube avec 5 allumettes et un carré avec 3 allumettes sans les casser bien entendu !

On possède en plus un miroir, une feuille de papier, un compas et de la colle, mais rien d’autre.

. 106°/ Les tas de feuilles :

Deux hommes ratissent leurs jardins. Le premier, qui s‘appelle Paul, fait 3 tas de feuilles et l’autre, qui s’appelle Popaul en fait 7. Sachant que Paul est un fainéant et que ces tas sont deux fois plus petits que ceux de Popaul, combien de tas y aura-t-il lorsqu’ils mettront leurs tas en commun ?

. 107°/ L’automobile :

Une automobile se trouve à 1 km d’une ville. A 1 km de la ville (là où est la voiture) se trouve 1 panneau de signalisation : 120km/h. A 1/2km : 1 panneau de 60km/h ; à 1/3km : 40km/h ; à 1/4km : 30km/h ; à 1/5km : 24km/h et à 1/6km : 20km/h. En supposant qu’elle roule à la vitesse maximale, combien de temps mettra-t-elle pour arriver à la ville ?

. 108°/ Les 31 maillons de la chaîne :

Je possède un collier qui se présente sous la forme d’une chaîne fermée de 31 maillons. Pour rémunérer une personne qui travaillera pour moi pendant 31 jours, je dois lui donner chaque soir un maillon de cette chaîne. Quel est le nombre minimum de maillons à couper pour tenir mes engagements et à quel endroit dois-je les couper ? (La personne peut rendre des maillons, par exemple un soir elle peut vous rendre 2 maillons et vous lui donnez une chaînette de 3 maillons).

. 109°/ Des trains, encore et toujours !

Nous sommes dans une ligne de métro circulaire. 24 trains s’y déplacent dans la même direction à intervalles réguliers et roulant tous à la même vitesse. Demain, on doit rajouter des trains afin de diminuer de 20% les intervalles entre deux trains. Combien y aura-t-il de trains supplémentaires demain ?

. 110°/ Le rectangle :

On plie soigneusement en deux une feuille de papier rectangulaire, cinq fois à la suite, en pliant à chaque fois suivant un pli perpendiculaire au pli précédent. Après cela on déchire les 4 coins du (petit) rectangle de papier obtenu. Ceci fait on déplie la feuille. Combien de vrais trous voit-on alors à l’intérieur de la feuille de papier ?

. 111°/ Les tonneaux de vin :

Trois hommes ont à se partager 21 tonneaux dont 7 sont pleins, 7 sont vides et 7 à demi-pleins. Comment faire le partage de sorte que tous les 3 aient un égal nombre de tonneaux et la même quantité de vin ?

. 112°/ L’arbre foudroyé :

Un arbre de 8 mètres de hauteur a été brisé par le vent. Le sommet touche la terre à 4 mètre du pied de l’arbre. A quelle hauteur a-t-il été brisé ?

. 113°/ Les deux mâts :

Un mât de 3 mètres et un mât de 6 mètres sont plantés verticalement sur un terrain plat. Deux cordes relient les sommets de chaque mât au bas de l’autre. A quelle hauteur se trouve le point d’intersection des deux cordes ?

. 114°/ Encore des allumettes :

Comment faire 8 triangles équilatéraux avec 6 allumettes ? Ou 7 triangles équilatéraux identiques avec 5 allumettes et de quoi réfléchir.

. 115°/ La course :

Castor et Pollux font une course de 100 mètres. Lorsque Castor termine la course, Pollux n’est qu’à 90 mètres. Ils décident de refaire la course, mais Castor partira 10 mètres derrière Pollux. Avec exactement les mêmes conditions que lors de la première course, y aura-t-il un vainqueur ?

. 116°/ Une question d’angles :

Sur une maison, les deux côtés du toit ne font pas le même angle avec l’horizontale. L’un fait un angle de 60°, l’autre un angle de 70°. Si un canard pond un œuf sur l’arête du toit, de quel côté cet œuf tombera-t-il ?

. 117°/ Les péniches :

Une péniche effectue un service régulier entre deux villes A et B situées sur un cours d’eau navigable (B est en aval de A). A la descente, la péniche met 3h, à la remontée, elle met 1h30 de plus. Combien de temps mettrait un corps flottant lâché en A pour atteindre la ville B ?

. 118°/ Hassan Céhef, tout est possible :

Le TGV file dans la campagne à une allure vertigineuse. Inquiet un passager va trouver Hassan Céhef, le conducteur. Celui-ci lui explique alors son problème :

– Entre Paris et Havresac, je dois faire une moyenne de 100km/h.

– Rien de plus facile : avec un TGV, pas besoin de foncer comme un malade.

– Oui, mais il se trouve que, pendant la moitié du trajet, à cause des travaux, je n’ai fait que 50km/h de moyenne. Alors maintenant, je dois forcer l’allure pour combler mon retard. Quelle doit être ma vitesse moyenne minimale sur la seconde partie du trajet pour tenir 100 km/h de moyenne sur la totalité du parcours ?

. 119°/ Bernard et Julie :

Bernard a cinq fois l’âge que Julie avait quand il avait le double de l’âge qu’elle a. La somme de l’âge que Julie aura quand elle aura l’âge que Bernard avait quand elle avait la moitié de l’âge qu’elle a, et de l’âge que Bernard aura quand elle aura deux fois l’âge qu’elle a est égal à l’âge de ce siècle. (Cette énigme a été écrite en l’an 2000). Quels sont leurs âges respectifs, sachant que ce sont des nombres entiers ?

. 120°/ Pierrot et Jeannot :

A l’instant même où Pierrot quittait le bar du Commerce pour se rendre au bar du Théâtre, Jeannot quittait le bar du Théâtre pour se rendre au bar du Commerce. Ils marchaient à vitesse constante. Quand ils se rencontrèrent, Pierrot remarqua tout haut qu’il avait parcouru 200 m de plus que Jeannot. Ce dernier, l’esprit embué par l’alcool, prit cette remarque comme une injure et se mit à se battre avec Pierrot. La bagarre terminée, chacun reprit son chemin mais avec une vitesse diminuée de moitié car tous deux étaient légèrement blessés. Pierrot arriva au bar du Théâtre au bout de 8 minutes et Jeannot au bar du Commerce au bout de 18 minutes. Quelle distance y-a-t-il entre les deux bars ?

. 121°/ 5 + 5 + 5 = 550 ?

Comment en un seul coup de crayon rendre l’équation suivante vraie : 5 + 5 + 5 = 550 ?

Il est interdit de transformer le signe = en signe différent.

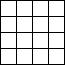
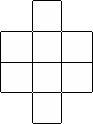
. 122°/ Les carrés :

Combien voyez-vous de carrés ?

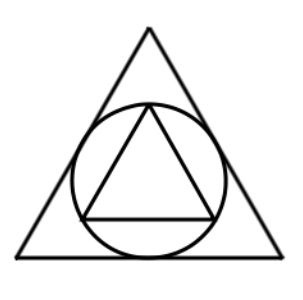
. 123°/ Le triangle de Curry :

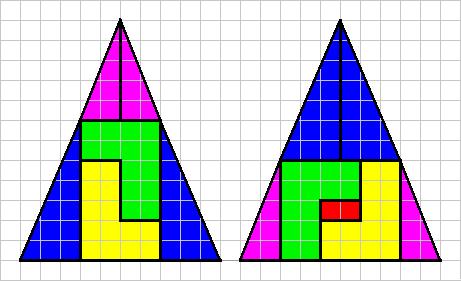
Les parties de la première figure ont été regroupées différemment pour former la seconde, à la différence qu’il faut ajouter à ce dernier deux petits carrés.
Comment expliquer la présence de ce rectangle rouge ?

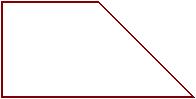
. 124°/ Trapèze :

Comment découper ce trapèze rectangle en 4 partie égales ?

. 125°/ Le tirage au sort :
Pour tirer au sort, cinq amis ont sorti les dix cartes de cœurs d’un jeu de cartes (de l’as au 10) et chacun a tiré deux cartes. En totalisant leurs points, ils ont obtenu respectivement : Thomas 12, Jessica 9, Thierry 11, Guillaume 6, Caroline 17. Thierry, toujours bavard, s’est écrié : « J’ai l’as !». Qui a eu le 7 ?

. 126°/ Les mégots de cigarettes :
N’ayant plus de cigarettes, un clochard se met à ramasser des mégots. Il en recueille 49, car il a appris qu’il faut 7 mégots pour faire une cigarette. Combien aura-t-il de cigarettes à fumer ?

. 127°/ L’éléphant et les bananes :
Un planteur de bananes se trouve confronté à un problème bien difficile. Comme moyen de transport, il ne dispose que d’un vieil éléphant qui consomme une banane au kilomètre et n’accepte de porter que 1000 bananes au plus sur son dos. Le plus proche marché se trouve à 1000 km de la plantation. Sa production s’élève à 3000 bananes. Montrer que ce planteur pourra mettre au moins 400 bananes en vente sur le marché ?

. 128°/ Les voiliers :
Trois voiliers font une course dont l’étape finale est Arcachon. Le deuxième voilier met 2 fois plus de temps que le premier et moitié moins de temps que le troisième. Sachant que le troisième voilier met 30 jours de plus que le premier, combien de temps met chaque voilier ?

. 129°/ L’équation :

ab x c = de

Dans cette équation, chaque lettre a, b, c, d et e représentent un chiffre de 1 à 5. Il n’y a pas 2 fois le même chiffre et ab et de sont des nombres à 2 chiffres. Trouvez la valeur des lettres.

. 130°/ Les puissances de 9 :
Quel est le chiffre qui termine 9¹⁹⁹⁹ + 1 ?

. 131°/ Carré de x, carré de x+1 :
Le carré de x s’écrit avec un 9, un 6 et un 1. Figurez-vous que cela reste vrai pour le carré de x+1… Quel est x ?

. 132°/ Le brocanteur :
Un brocanteur achète une vieille montre 100 F, la vend 120 F, la rachète 140 F et la revend 160 F. Quel est son bénéfice ?

. 133°/ 3024 :
3 024 est le produit de 4 nombres entiers consécutifs. Quels sont-ils ?

. 134°/ Encore un train !!!
Si l’on augmente la vitesse d’un train de 30km/h, on gagne 1 heure sur le trajet. En revanche si on diminue la vitesse de 30km/h on perd 2 heures. Quelle est la longueur du trajet ?

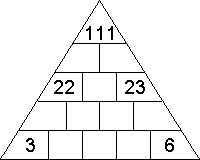
. 135°/ Les fléchettes et la cible :
On dispose de trois flèches et d’une cible possédant 1 centre et 4 couronnes. Le centre vaut 23 points puis respectivement de la couronne intérieure à la couronne extérieure, 12, 8, 3, 1 points. Une flèche à l’extérieur de la cible vaut 0 point. Quel est le plus petit score total (c’est à dire la somme des points obtenus par les trois flèches) impossible à obtenir ?

. 136°/ Godzilla, le retour :
Sans la tête il mesure 2,90m. Sans la queue, il mesure 2,50m. Son corps est aussi long que sa tête et sa queue réunies. Combien mesure ce monstre de la tête à la queue ?

. 137°/ Les minutes :
Combien de minutes avant six heures est-il s’il y avait, il y a cinquante minutes, quatre fois autant de minutes après quatre heures ?

. 138°/ La fumée du train :
Un TGV se déplace vers le sud-est à 180km/h, le vent souffle de l’ouest vers l’est à 30km/h. Dans quelle direction la fumée du train soufflera-t-elle ?

. 139 °/ La moyenne d’âge :
Dans une salle, 9 personnes sont assises: leur moyenne d’âge est de 25 ans. Dans une autre salle, 11 personnes sont réunies : leur moyenne d’âge est de 45 ans. Maintenant les deux groupes de personnes sont rassemblés. Quelle est, désormais, la moyenne d’âge du groupe ainsi constitué ?

. 140°/ Les Pokemons :
Après deux réductions successives de 20% chaque fois, mon Pokemon coûte 320F(ça vaut une petite fortune ces trucs-là). Quel était le prix du Pokemon avant les réductions ?

. 141°/ La liste :
Je recopie tous les entiers de 1 à 30 inclus et raye certains d’entre eux de telle manière que dans la liste restante aucun nombre ne soit le double d’un autre. Quel est le nombre maximum d’entiers dans la liste restante ?

. 142°/ La vielle montre :
Ma vieille montre retarde de 8 minutes par 24 heures. De combien de minutes dois-je l’avancer ce soir à 22h si j’ai absolument besoin qu’elle me donne l’heure exacte demain matin à 7h ?

. 143°/ Le poisson encerclé :

Le rivage d’un lac décrit un cercle parfait.

Une truite se met en branle à un point du rivage et nage vers le nord sur une distance de 600 mètres avant de se heurter au rivage opposé.

La truite nage ensuite sur 800 mètres vers l’est avant de se heurter à nouveau au rivage.

Quel est le diamètre du lac ?

. 144°/ Les deux cyclistes :
Pierre et Paul veulent comparer leurs vitesse à bicyclette bien qu’ils ne possèdent qu’un seul engin. Aussi, sur une route bien plate et pavée de bornes kilométriques, Pierre pédale du kilomètre un au kilomètre douze ; Paul étant derrière pour chronométrer. Puis, du kilomètre douze au kilomètre vingt-quatre, Paul pédale, Pierre étant derrière pour chronométrer. Pierre gagne haut la main. N’aurait-on pas pu prévoir ce résultat ?

. 145°/ 3 égal 0 :
On prend l’équation : x² + x + 1 = 0 (équa.1) avec x?0

(équa.1) × x donne x³ + x² + x = 0 cad x³ + x² + x + 1 = 1 (équa.2)
Donc : (équa.2 – équa.1) donne x³=1
donc : x =1

On remplace x =1 dans (équa.1) et on obtient 1+1+1=0
3 = 0

Comment est-ce possible ?

. 146°/ La petite vendeuse œufs:
On demande à une vendeuse d’œufs combien d’œufs elle a vendus en une journée. Elle explique que son premier client lui a dit « Je t’achète la moitié de ton stock d’œufs plus la moitié d’un œuf. » Puis, ses deuxièmes et troisièmes clients lui dirent la même chose. Une fois remplies ces trois commandes, il ne me reste plus d’œufs et elle n’en avait cassé aucun. Combien d’œufs a-t-elle vendus ce jour-là ?

. 147°/ Troncature et arrondi :
La troncature au dixième de l’arrondi au centième de ma taille en mètres vaut 1,6 m. Combien puis-je mesurer ?

. 148°/ L’énigme du cube :
Trouvez le plus petit nombre strictement supérieur à 1 qui soit égal à la somme des chiffres de son cube.

. 149°/ Générosité :
Rencontrant un mendiant, un homme lui donne une pièce ; il en rencontre un deuxième, et lui donne deux pièces. Il rencontre d’autres mendiants encore, à qui il donne une pièce de plus que précédemment à chaque fois… jusqu’à ce qu’il n’ait plus rien n’en poche. Il réfléchit alors et se dit : « Si j’avais donné autant de pièces à chacun d’entre eux, cela aurait été plus équitable et chaque mendiant aurait reçu 8 pièces ». Combien a-t-il rencontré de mendiants ?

. 150°/ Le forain :
Un forain interpelle ainsi les passants : « Regardez ces quatre billets, deux d’entre eux sont gagnants et les deux autres sont perdants. J’en mets un ou plusieurs dans chacune de ces deux enveloppes. Pour 10F, vous choisissez une enveloppe et dans l’enveloppe vous choisissez un billet, vous avez donc une chance sur deux de gagner un lot ! » Le forain a-t-il raison ?

. 151°/ Dr Knock : La Dame tombée de l’échelle :
La dame – Mon dieu, mon dieu ! J’ai bien du malheur de tomber de cette échelle !
Knock – Pour vous guérir, cela va vous coûter une vache, un veau, un cochon et un poulet.
La dame – C’est une désolation, Jésus Marie ! Pensez que j’avais payé 108210 F pour cinq vaches, sept veaux, neuf cochons et un poulet. Une vache vaut 4000 F de plus qu’un veau, trois veaux autant que dix cochons et trois milles poulets autant que cinq veaux ! Aie, aie, aie, que vais-je devenir ?
Combien la dame doit payer à Knock pour sa guérison ?

. 152°/ L’infini :
On peut démontrer que 1,9999 avec une infinité de 9 est égal à 2.

Démonstration : on pose X = 1,99999999….

Donc : 10X – X = 19,999999999…. – 1,999999999 = 18 (puisqu’on a une infinité de 9 à la fin des nombres)
Moralité, 9X = 18 c’est à dire X = 2. Comment expliquer l’erreur ?

. 153°/ Un petit chiffre :
Quelle est le nombre entier de trois chiffres, en dehors de zéro, dont la somme est 15 et dont le chiffre des dizaines est le quadruple de celui des unités ?

. 154°/ Le compte est bon :
Comment écrire 120 avec 8, 8, 8, 8 ?

. 155°/ Les 4 enfants :
Quatre gamins, André, Bernard, Claude et Daniel, se rendent à la confiserie pour dépenser tout leur argent de poche. Ils achètent des bouchées à 0,60 F, des caramels à 0,50 F, des sucettes à 0,40 F et des chewing-gums à 0,30 F. André choisit 22 unités de sa friandise préférée, Bernard 18, Claude 15 et Daniel 24. Pour payer, ils mettent leur argent en commun. Ils disposent de pièces de 10 F, 5 F et 1 F, d’une pièce de 0,50 F et une de 0,10 F. Qui a choisi les caramels ?

. 156°/ Les multiples de 17 :
Trouver un nombre ABCDEFG de sept chiffres différents, tel que chacun des cinq nombres ABC, BCD, CDE, DEF et EFG soit multiple de 17.

. 157°/ Les excursions en Grèce :
Quatre excursions culturelles sont proposées à cent vacanciers qui coulent de paisibles heures de plage dans un hôtel de Grèce : 49 personnes s’inscrivent pour Thèbes, 42 pour Rhodes, 35 pour Athènes, et 30 pour Delphes. Si le total excède 100, c’est que 24 courageux ont pris une option pour deux excursions, 10 autres se sont inscrits pour trois excursions, et il se trouve même en plus quelques acharnés pour faire les quatre circuits. Bien sûr, il y en a comme toujours qui restent à bronzer idiots sans faire la moindre excursion, mais ils se comptent sur les doigts de la main. Combien y a-t-il d’acharnés ? Combien ne font aucune excursion ?

. 158°/ Cinq couples :

Cinq hommes (M. Aladin, M. Bertrand, M. Chartrand, M. Danis et M.Emond) ont décidé d’épouser cinq demoiselles (Mlle Aladin, Mlle Bertrand, Mlle Chartrand, Mlle Danis et Mlle Edmond) en respectant les conditions suivantes:

Aucun homme n’épousera son homonyme féminin.
Si un homme M. X épouse Mlle Y, alors M. Y ne peut épouser Mlle X, et ce pour toutes les possibilités de X et Y.
M.Emond épousera la femme dont l’homonyme masculin épousera Mlle Danis.
M. Aladin épousera la femme dont l’homonyme masculin épousera la femme dont l’homonyme masculin épousera la femme dont l’homonyme masculin épousera Mlle Bertrand.

Question: Quels sont les noms des membres des cinq futurs couples (nom du mari et nom de jeune fille de la mariée, bien sûr !)

. 159°/ Problème d’âge : C’est dur de vieillir

Quand Francine avait un an de plus que Diane avait, quand Francine avait deux foi l’âge que Diane avait, quand Francine avait la moitié de l’âge que Diane a maintenant, et bien Diane avait la moitié de l’âge que Francine avait, quand Diane avait la moitié de l’âge que Francine a maintenant.

Une de ces personnes est dans la soixantaine. Je vous demande l’âge de Francine.

. 160°/ À qui appartient le zèbre et qui boit de l’eau ?

Voici plusieurs indices. À partir ce ceux-ci, déterminez qui boit de l’eau et qui est le propriétaire du zèbre.

Cinq maisons de couleurs différentes sont habitées par des hommes de nationalités et de professions différentes. Chacun a son animal favori et sa boisson préférée.
L’Anglais habite la maison rouge et le Japonais est acrobate.
Le chien appartient à l’Espagnol.
On boit du café dans la maison verte. Cette dernière est d’ailleurs située immédiatement à droite de la maison blanche.
L’Ukrainien boit du thé.
Le sculpteur élève des escargots.
Le diplomate habite la maison jaune.
C’est dans la maison du milieu qu’on boit du lait.
La maison d’extrême gauche est habitée par le Norvégien.
Le médecin habite la maison voisine de celle où demeure le propriétaire du renard.
La maison du diplomate est voisine de celle où il y a un cheval.
Le violoniste boit du jus d’orange.
Le Norvégien demeure à côté de la maison bleue.

À qui donc appartient le zèbre ? Et qui donc boit de l’eau ?

. 161°/ Aurélie et les bonbons :

Lorsque Aurélie entra dans le magasin, ses yeux restèrent accrochés à un comptoir de bonbons. Sur celui-ci, il y avait deux différentes sortes de bonbons.

Le propriétaire du magasin les avait mélangés et arrangés sous forme de carré, les bonbons ayant tous la même dimension.
– Pardon monsieur, dit Aurélie, mais combien coûte cet ensemble de bonbons ?
– Oh ! Dans ce carré il y a les deux sortes de bonbons, dit l’homme. Une sorte à 5 sous l’unité et l’autre à 14 sous l’unité. Cet ensemble carré de bonbons fait donc un total de 5$.

Aurélie acheta et mangea dans la journée tous les bonbons. Ayant été très malade, elle se demanda alors combien de bonbons de chaque sorte elle avait mangés.

Pouvez-vous aider Aurélie à résoudre correctement se problème ?

À noter que 100 sous = 1$.

. 162°/ Fischer vs Spassky:

À Sinusville, deux clubs d’échecs (le club Spassky et le club Fischer) font une compétition. Les cinq meilleurs membres des deux clubs jouent les uns contre les autres. C’est-à-dire que les cinq membres du club Spassky rencontrent les cinq membres du club Fischer une et une seule fois.

Chaque joueur joue donc 5 parties, et ce à raison d’une partie par jour. Ils jouent les lundi, mardi, mercredi, jeudi et vendredi d’une même semaine.

L’histoire ne dit pas qui remporta le match ; cependant, à l’aide des indices ci-dessous, pouvez-vous nommer les adversaires des cinq parties du lundi, du mardi, etc.

Alain, Bernard, Claude, Denis et Étienne sont les meilleurs membres du club Spassky ;

Albert, Bertrand, Christian, Didier et Emmanuel sont les meilleurs membres du club Fischer ;

Les parties Alain-Bertrand et Claude-Albert se sont tenues le même jour ;

Il en fut de même des parties Claude-Didier et Denis-Christian et les parties Alain-Emmanuel et Denis-Albert.

La partie Etienne-Christian s’est tenue le lundi (ce qui ne fut pas le cas pour la partie Claude-Bertrand), la partie Alain-Albert s’est tenue le mardi, la partie Claude-Emmanuel le mercredi et la partie Denis- Didier, le jeudi.

. 163 °/Charité bien ordonnée…

-J’ai fait une bonne affaire, me dit le curé
-Laquelle donc, demandai-je, curieux.
-Voilà, répondit-il. Ce matin, je suis parti avec un certain montant d’argent et sur mon chemin j’ai rencontré trois «quêteux». Profession oblige, je donnai au premier 1 F de plus que la moitié de ce que j’avais en poche, au second 2 F de plus que la moitié de ce qui me restait alors, et au troisième, 3 F de plus que la moitié de ce qui me restait à ce moment-là.
– Vous reste-t-il de l’argent ? demandai-je.
– Mais bien sûr mon frère; il me reste 1F.
– Je ne comprends pas où est cette si bonne affaire, lui fis-je remarquer en me grattant la tête.
– Mais c’est l’évidence même! Puisque Dieu remet au centuple toute bonne action, il me doit donc …
et le curé me donna le montant. Saurez-vous le trouver ?

. 164°/ Le portrait :

Vous rencontrez un homme dans un musée qui contemple un portrait au mur. Lorsque vous mentionnez que vous trouvez le tableau de votre goût, il vous dit, en pointant le portrait : « En effet! Mais saviez-vous que le père de cet homme est le fils de mon père, et que je suis enfant unique ? »

Pouvez-vous sur la base de cette confidence un peu bizarre déterminer qui est la personne représentée ?

. 165°/ L’encyclopédie et le ver :

Quatre volumes d’une encyclopédie sont placés sur une tablette. L’ensemble des pages de chaque volume mesure exactement deux pouces d’épaisseur, tandis que les couvertures ont chacune 1/6^e de pouce d’épaisseur.

Un ver commence à grignoter à partir de la page 1 du Volume I, et continue de manger jusqu’à la dernière page du Volume IV.

Quelle est la distance parcourue par le ver ?

. 166°/ Les chaussettes :

Un tiroir contient dix chaussettes noires et quinze chaussettes bleues, pêle-mêle.

Vous désirez en retirer une paire, qu’importe la couleur, mais l’ampoule est brûlée et il fait trop noir pour distinguer les couleurs.

Quel est le nombre minimum de chaussettes que vous devez retirer du tiroir pour vous assurer d’obtenir une paire assortie ?

. 167 °/Les quatre cartons :

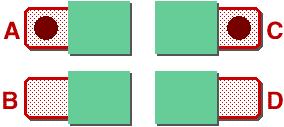
Sur une table, il y a quatre cartons, identifiés A, B, C, et D, ayant chacun une moitié cachée et une moitié visible.

Lesquelles des quatre cartons devez-vous absolument découvrir afin de pouvoir répondre à la question suivante avec certitude ?

Pour chaque carton de cet ensemble, est-il vrai que s’il y a un cercle à gauche, il y a un cercle à droite ?

Remarquez que vous devez décider une fois pour toutes ; vous n’avez pas le loisir de découvrir les cartons un à un. Il faut identifier dès le départ tous les cartons que vous devez nécessairement découvrir pour répondre à la question tout en ayant la certitude que votre réponse soit bonne.

Imaginez que vous devez débourser un dollar par carton découvert ; vous cherchez donc à découvrir le minimum de cartons et ainsi dépenser le moins possible.

. 168°/ Les quatre dessins :

On vous présente quatre dessins confectionnés à partir de deux couleurs et de deux formes : un losange bleu, un losange rouge, un cercle bleu et un cercle rouge.

En les confectionnant, le concepteur avait en tête une forme particulière et une couleur particulière telles que, si un dessin possédait une et une seule de ces particularités, il le nommait ‘bidule.’

Selon les particularités qu’il avait en tête, le losange bleu est un bidule.

Lequel des trois autres dessins pourrait l’être aussi ?

. 169°/ Les quatre fiches :

On vous présente quatre fiches, sur chacune desquelles est inscrit le nom d’une ville sur une face, et de l’autre, un mode de transport. On dispose les quatre fiches sur une table.

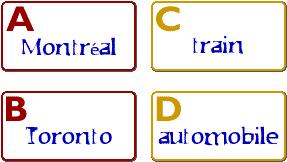
Vous devez décider quelles fiches vous devez nécessairement retourner pour en inspecter l’envers afin de déterminer si l’énoncé suivant est vrai :

Chaque fiche ayant ‘Montréal’ d’un côté a ‘train’ de l’autre.

. 170°/ La première fois :

Sur l’île des chevaliers et des brigands, chaque habitant est soit un chevalier, soit un brigand.

Les chevaliers disent toujours la vérité, et les brigands mentent toujours.

Vous êtes en visite sur l’île et vous rencontrez un habitant qui vous dit : « Ceci n’est pas la première fois que je dis ce que je dis en ce moment. »

Est-il un chevalier ou un brigand ?

. 171°/ Le verger :

On vous demande de planter un petit verger, mais disposé d’une façon bien spéciale.

Il faut que les pommiers soient plantés en cinq rangées de quatre arbres chacune.

La commande n’est pas bien difficile. En effet, il suffit d’acheter vingt petits pommiers.

Mais voilà que la vie ne vous sourit pas ce jour-là, car le pépiniériste ne peut vous offrir que dix pommiers de la variété que vous désirez.

Vous repartez bredouille, mais, tout d’un coup, un flash ! Vous réalisez qu’il est possible de répondre à l’exigence de la disposition avec seulement dix arbres, et en bonus vous réduisez les coûts de moitié.

Comment disposer les arbres ?

. 172°/ Le verger bis :

On vous demande de planter un petit verger, mais disposé d’une façon bien spéciale. Il faut que les pommiers soient plantés en six rangés de quatre arbres chacune. La commande n’est pas bien difficile. En effet, il suffit d’acheter vingt-quatre petits pommiers et de les placer comme dans le dessin à droite, par exemple.

Mais voilà que la vie ne vous sourit pas ce jour-là, car le pépiniériste ne peut vous offrir que douze pommiers de la variété que vous désirez. Vous allez repartir en état de profonde déception, mais, tout d’un coup, un flash ! Vous réalisez qu’il est possible de répondre à l’exigence de la disposition avec seulement douze arbres, et en bonus vous réduisez les coûts de moitié.

Comment disposer les arbres ?

Pouvez-vous trouver une deuxième disposition qui répond aux mêmes contraintes ?

. 173°/ Le verger encore :

On vous demande de planter un petit verger mais disposé d’une façon bien spéciale. Il faut que les pommiers soient plantés en dix rangés de trois arbres chacune. La commande n’est pas bien difficile. En effet, il suffit d’acheter trente petits pommiers.

Mais voilà que la vie ne vous sourit pas ce jour-là, car le pépiniériste ne peut vous offrir que neuf pommiers de la variété que vous désirez. Vous allez repartir en état de profonde déception, mais, tout d’un coup, un flash ! Vous réalisez qu’il est possible de répondre à l’exigence de la disposition avec seulement neuf arbres, et en bonus vous réduisez les coûts de façon appréciable.

Comment disposer les arbres ?

. 174°/ Encore une suite :

Quel est le prochain chiffre dans la suite suivante ?

. 175°/ La loco en flammes :

Un train passager pénètre la frontière sud d’une immense forêt carrée de 500 km sur 500 km. Le train se dirige vers le nord, et sa vitesse de croisière maximale est de 100 km/h. Ce jour-là, il y a un vent du sud soufflant à 200 km/h (ce vent n’a pas d’influence sur la vitesse du train). Une heure plus tard, un feu de forêt d’une intensité incroyable se déclare à la largeur complète de la frontière sud de la forêt. Le vent pousse le feu vers le nord à 200 km/h. Le conducteur du train en est averti par radio. Un calcul rapide lui apprend qu’il ne peut en cas distancer le feu qui va rattraper le train avant qu’il ne puisse sortir de la forêt. Il stoppe le train et fait quelque chose… Que fait-il qui épargnent le train et les passagers

. 176°/ Les trois sports :

De trois amis, deux jouent au golf, deux jouent à la pétanque et deux jouent au tennis.

Celui qui ne joue pas au tennis ne joue pas à la pétanque et celui qui ne joue pas à la pétanque ne joue pas au golf.

Quels sports sont pratiqués par chaque ami ?

. 177°/ La fête des enfants :

Un petit garçon est de retour d’une fête pour des enfants et, tout excité, n’arrive pas à répondre tout à fait clairement aux questions de sa mère.

Il se rappelait qu’il y avait cinq fillettes à la fête, que Berthe portait du bleu et qu’Édith portait du rouge.

Il ne se rappelait plus de la couleur portée par Marguerite, mais était certain que ce n’était pas le jaune.

Il a affirmé que Solange et la fillette en vert ont gagné au ping-pong contre Berthe et la fillette en jaune.

Et, il trouvait la fillette vêtue de brun la plus sympathique.

Quelle couleur était portée par Jeannine et quel est le nom de la fillette la plus sympathique ?

. 178°/ L’île des cannibales III :

	Sur l’île des cannibales, il y a deux villages : le village des cannibales qui mentent toujours et le village des végétariens qui disent toujours la vérité. Vous vous approchez de l’île en canot, et vous apercevez trois habitants de l’île sur la plage, A, B et C.
	Vous demandez à A : « Êtes-vous cannibale ou végétarien ? » A répond, mais malheureusement, le bruit des vagues enterre sa réponse.
	Vous demandez à B : « Qu’est-ce qu’il a dit? » B répond :  » Il a dit qu’il est cannibale. » Aussitôt, C dit: « Ne l’écoutez pas, il est menteur ! »
Que sont B et C?

. 179°/ Alain et Bernard :

Si Alain et Bernard effectuent ensemble un travail en 8 jours …

Et si Alain seul fait le même travail en 10 jours …

Combien de temps mettra Bernard pour faire ce même travail tout seul ?

. 180°/ Les trois métiers :

Trois amis pratiquent trois métiers différents. Leurs noms correspondent à leurs métiers, mais pas nécessairement respectivement.

Les énoncés suivants ont été faits au sujet des trois amis, mais seulement un est vrai :

A – Monsieur Charpentier n’est pas boulanger.

B – Monsieur Masson n’est pas charpentier.

C – Monsieur Charpentier est charpentier.

D – Monsieur Masson n’est pas boulanger.

Qui est quoi ?

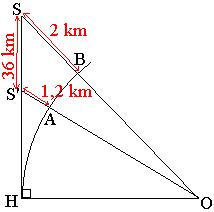
. 181°/ L’oncle Guillaume :

L’oncle Guillaume nous rejoint toujours pour le déjeuner du dimanche. Mais la distance qui sépare nos deux maisons est trop grande pour que l’oncle fasse tout le trajet à pied, malgré sa prédilection pour la marche. Alors, il a été convenu que je roulerais en voiture vers sa maison et que je le cueillerais en chemin, lui évitant ainsi de parcourir à pied une bonne partie de la route.

L’oncle Guillaume et moi sommes très méthodiques. Il part toujours à la même heure et marche toujours à la même vitesse ; je pars toujours à la même heure et je roule toujours à la même vitesse. En conséquence, je le rencontre au même point sur la route et nous arrivons à la maison à la même heure, à chaque semaine.

Dimanche dernier, quelque chose d’inhabituel s’est produit, j’ai dû rouler plus loin que d’habitude avant de le rencontrer et nous sommes arrivés à la maison 10 minutes en retard.

Lorsque je lui ai demandé ce qui s’était passé, il m’a dit qu’il était parti à l’heure habituelle mais qu’il s’était arrêté un moment pour regarder une partie de pétanque disputée par des gens de son quartier.

Je conduis à 36 km/h. L’oncle Guillaume marche à 3 km/h. (On peut négliger les accélérations et décélérations…)

Pendant combien de temps l’oncle Guillaume a-t-il flâné près du terrain de pétanque ?

. 182°/ Le poisson encerclé :

Le rivage d’un lac décrit un cercle parfait.
Une truite se met en branle à un point du rivage et nage vers le nord sur une distance de 600 mètres avant de se heurter au rivage opposé.
La truite nage ensuite sur 800 mètres vers l’est avant de se heurter à nouveau au rivage.
Quel est le diamètre du lac ?

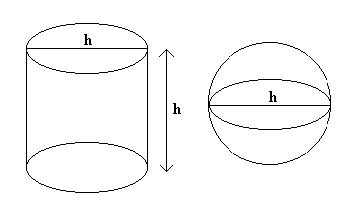
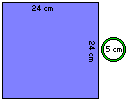
. 183°/ Le ballon et la planète :

On effectue les deux expériences suivantes :

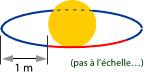
1 On entoure un ballon d’un diamètre de 20 cm avec une ficelle rouge.
On rallonge cette ficelle rouge avec une ficelle bleue pour former un cercle parfait autour du ballon à une distance de 1 mètre.
2 Avec une (très!) longue ficelle verte de 40 000 km, on fait le tour de notre planète Terre à l’équateur. (On suppose la Terre parfaitement sphérique et sans relief…)
Ensuite, on rallonge la ficelle verte avec la ficelle bleue de l’expérience précédente pour former un cercle concentrique parfait autour de la Terre.
À quelle distance du sol est cette ficelle?

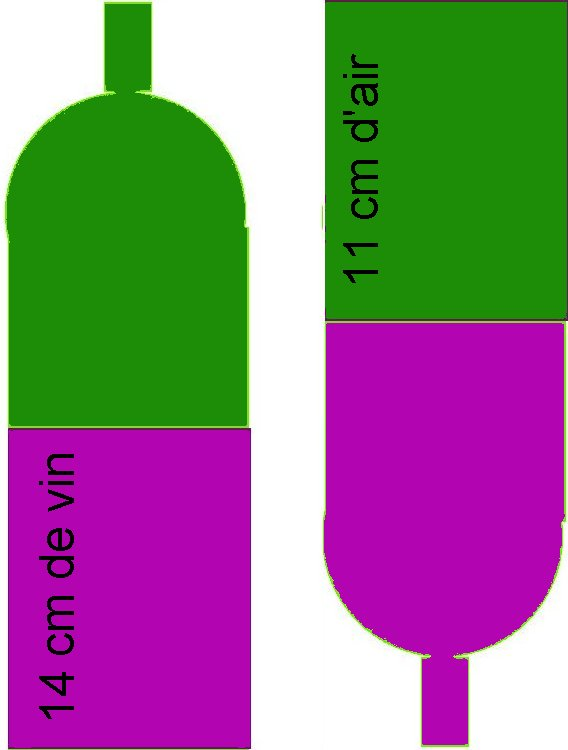
. 184°/ Plus tu pédales moins vite, et moins tu avances plus vite… !!

Roger habite près d’une rivière qui en hiver a un assez fort courant alors qu’il est quasi nul en été. L’hiver, Roger met 2 heures pour descendre le courant jusqu’à un certain point et 3 heures pour remonter à son point de départ.

Combien mettra-t-il de temps en été pour faire le même parcours (aller ou retour) ?

(On suppose évidemment qu’il rame toujours à la même allure.)

. 185°/ Les amis en skis :

Un débutant sur une pente de ski dévale la pente en ligne droite à la même vitesse que le remonte-pente qui le ramène en haut de la pente.

Son ami, qui est un pro du ski, lui fait le pari qu’il peut parcourir le même trajet (la monté en remonte-pente et la descente) , mais en mettant 2 fois moins de temps qui lui et sa vitesse d’escargot.

Le débutant devrait-il risquer de relever le pari ?

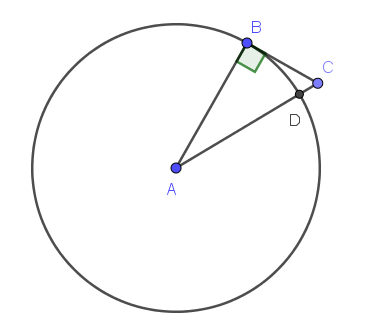
. 186°/ Les trois cartes :

Trois cartes sont posées les unes à côté des autres. Retrouvez leurs places exactes avec les 4 indices suivants :

1- un deux est à droite d’un roi (mais pas nécessairement côte à côte)
2- un carreau est à gauche d’un pique (mais pas nécessairement côte à côte)
3- un as est à gauche d’un cœur (mais pas nécessairement côte à côte)
4- un cœur est à gauche d’un pique (mais pas nécessairement côte à côte)

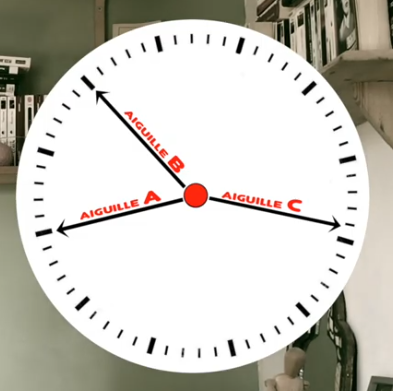
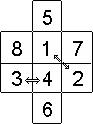
. 187°/ L’angle du cube :

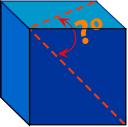
Calculez l’angle décrit par les deux lignes pointillées sur les faces du cube…

. 188°/ Les prisonniers de la tour :

Une Reine, sa fille la Princesse et le Fils de la princesse sont prisonniers dans une tour.

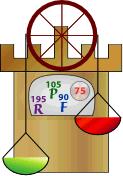
Leurs poids respectifs : 195 livres, 105 livres et 90 livres.

La seule voie de communication avec le sol est un câble enfilé dans une poulie auquel sont fixés deux paniers, un à chaque bout, de telle sorte que lorsqu’un panier touche au sol, l’autre est vis-à-vis la fenêtre.

Bien sûr, si un panier est chargé plus lourdement que l’autre, le plus lourd descend vers le sol. Cependant, si un panier comporte une surcharge de plus de 15 livres par rapport à l’autre, la descente devient trop rapide et donc dangereuse pour les prisonniers, car il n’y a aucun moyen de ralentir la descente une fois amorcée.

Tout ce dont les trois prisonniers disposent dans leur tour est un boulet de canon pesant 75 livres.

Ils ont réussi à s’échapper de la tour, sains et saufs…

Comment ont-ils fait ?

. 189°/ Les quatre cartes :

On étale les quatre cartes suivantes sur une table.

Chaque carte comporte une lettre d’un côté et un nombre de l’autre.

On vous propose une règle au sujet de ces cartes, et on vous demande lesquelles vous devez obligatoirement retourner afin de vérifier si de fait la règle tient pour l’ensemble des cartes.

Imaginez que vous devez débourser un dollar par carte retournée ; votre objectif est donc de retourner le minimum de cartes et alors débourser la plus petite somme d’argent, tout en vous assurant que la règle est valable pour toutes les cartes.

La règle proposée :

Si une carte a une voyelle d’un côté, elle a un nombre pair de l’autre côté.

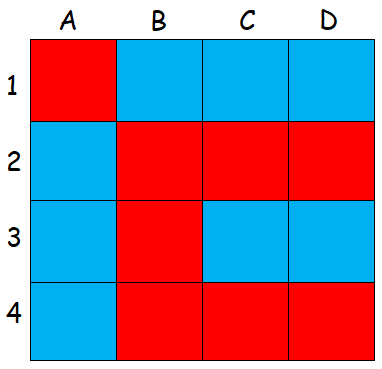
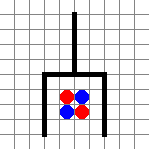
. 190°/ Les huit chiffres :

Le défi : placer chacun des chiffres de 1 à 8 dans les cases du dessin de telle sorte que des chiffres consécutifs ne se retrouvent pas dans des cases adjacentes, ni horizontalement, ni verticalement ni en diagonale.

. 191°/ Les trois interrupteurs :

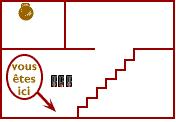
Vous vous trouvez au rez-de-chaussée d’une maison, en bas de l’escalier qui mène à l’étage.

Dans une chambre à l’étage, il y a un globe lumineux que vous désirez allumer.

Malheureusement, vous ne pouvez pas déterminer du rez-de-chaussée si ce globe est allumé, car la porte de la chambre est fermée et la pièce n’a aucune fenêtre.

Tout près de vous sont trois interrupteurs en position baissée (courant interrompu).

Vous ne pouvez monter l’escalier qu’une seule et unique fois pour trouver à coup sûr le bon interrupteur. Vous pouvez par contre lever ou baisser les interrupteurs à votre guise.

Comment faire pour déterminer lequel des trois interrupteurs actionne le globe lumineux de l’étage ?

. 192°/ L’île des cannibales :

Vous êtes sur une île sur laquelle il y a deux villages ; un est habité par des cannibales qui mentent toujours, et l’autre par des végétariens qui disent toujours la vérité.

Vous êtes en promenade sur un sentier et vous voulez vous rendre au village des végétariens. Vous arrivez à un embranchement dans le sentier et vous savez que l’une des branches du sentier se rend au village des cannibales et l’autre à celui des végétariens.

Malheureusement, il n’y a pas de panneau de signalisation pointant vers le village des végétariens.

Il y a cependant un habitant de l’île à l’embranchement et vous ne pouvez lui posez qu’une et une seule question (vous ne voulez quand même pas lui donner le temps de creuser son appétit s’il était par malheur un cannibale !).

Il semble disposé à converser, mais vous ne savez pas de quel village cet habitant provient, et donc vous ne savez pas s’il vous dira la vérité ou s’il vous mentira.

Quelle est votre question ?

. 193°/ L’examen de Paul :

Paul est en retard pour son examen de reprise auprès de son professeur de logique ; le professeur, accompagné de trois dames (A, B et C), est sur le point de quitter le bureau lorsque Paul arrive.

Plutôt que de remettre à plus tard l’examen, le professeur chuchote quelque chose aux trois dames, puis dit tout haut à Paul : « Une de ces dames dit toujours la vérité, une autre ment toujours et une troisième alterne systématiquement entre la vérité et la fausseté. Or, l’une d’entre elles est mon épouse. Tu peux leur poser toutes les questions voulues pendant dix minutes. Si tu peux me dire laquelle est mon épouse, tu auras 100% pour ton examen. »
Paul réfléchit quelques instants, puis demande à chacune si elle est l’épouse du professeur; elles répondent toutes « Oui. »
Puis il demande à A et à B si C a menti; A dit « Oui, » mais B dit « Non. »
Enfin, il demande à C si elle a menti; elle répond « Non. »

Sur cette base, Paul a pu trouver laquelle était l’épouse de son professeur et, de plus, il a pu identifier la menteuse, celle qui alternait et celle qui disait toujours la vérité.

Pouvez-vous en faire autant ?

. 194°/ Le postier fainéant :

Vous êtes un postier et vous aimez bien minimiser vos efforts. Un règlement des Postes stipule que :

Une lettre scellée doit être affranchie d’un timbre de 45cts.

Si le seul règlement que vous devez contrôler est celui-là, lesquelles des lettres suivantes qui passent devant vous sur le convoyeur devez-vous nécessairement retourner pour vous acquitter de votre tâche ?

Le but de la manœuvre est de retourner le minimum de cartes et ainsi dépenser le minimum d’énergie pour assurer la sieste à venir, tout en vous acquittant adéquatement de votre tâche.

. 195°/ Les filles du roi :

Un roi a deux filles jumelles, Amélie et Émilie.
Amélie ment toujours et Émilie dit toujours la vérité.
Une des filles est mariée, l’autre pas.

Un jeune homme désire épouser une fille du roi ; il avoue son désir au roi, qui lui propose le test suivant:

« Détermine le nom de ma fille qui est mariée, au moyen d’une question comportant au plus trois mots, posée à une seule des deux filles, sans savoir à laquelle tu t’adresses.
Si tu réussis, tu as ma permission de marier ma fille célibataire, si jamais elle le désire. »

Si vous étiez le jeune homme, quelle question poseriez-vous ?

(Note : vous pouvez considérer qu’un mot composé avec trait d’union compte pour un seul mot…)

. 196°/ L’ours :

Un bon matin, un chasseur se lève de bonne heure, prend son petit déjeuner et part à pied vers le sud. À un demi-kilomètre de son camp, il trébuche et s’écorche le nez. Il se relève et reprend sa route vers le sud en maugréant. Un demi-kilomètre plus loin, il aperçoit un ours. Il vise l’ours avec sa carabine, mais il avait oublié d’enlever le cran de sécurité. Il enlève le cran, mais l’ours entend le bruit de déclic et s’enfuit vers l’est à toute allure. Un demi-kilomètre plus loin, le chasseur rattrape l’ours et l’atteint de deux balles, blessant l’animal sérieusement ; l’ours poursuit sa fuite vers l’est. Le chasseur le prend en chasse et, un demi-kilomètre plus loin, réussit à l’abattre. Fier de sa capture, le chasseur marche un kilomètre vers le nord et regagne son camp. Désespéré, il s’aperçoit qu’entre-temps un autre ours avait ravagé son camp.

De quelle couleur était l’ours qui ravagea le camp ?

. 197°/ L’escargot dans le puits :

Un escargot repose au fond d’un puits d’une profondeur de trente pieds.

Il peut avancer de trois pieds en une journée, mais pendant la nuit il glisse de deux pieds vers le bas.

Combien de temps prendra-t-il pour sortir du puits ?

. 198°/ Le renard, le canard et le maïs :

Une dame arrive à une rivière, transportant un renard, un canard et un sac de maïs. Il y a un canot disponible, mais tellement petit qu’elle ne pourrait transporter qu’un seul de ses trois charges à la fois.

Elle ne peut pas laisser le renard et le canard ensemble sans surveillance, car le renard mangerait le canard. De même, elle ne peut pas laisser le canard et le maïs ensemble, car le canard boufferait le maïs.

Comment peut-elle transporter ses trois charges sur l’autre rive ?

. 199°/ L’enfant inconsolable dans le cimetière :

Dans un cimetière, vous rencontrez un enfant qui pleure amèrement sur une tombe. La tombe est visiblement fraîche, car il n’y a pas encore de pierre tombale.

Vous parlez un peu avec lui dans le but de le consoler, mais en vain.

Vous lui demandez finalement qui gît sous terre ici, et il vous répond tout sanglotant:
« Le père de la personne qui gît ici est le beau-père de mon père. »

Pouvez-vous sur la base de cette information déterminer qui est la personne récemment inhumée ?