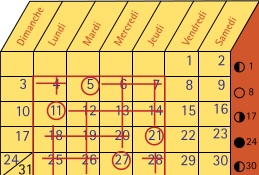
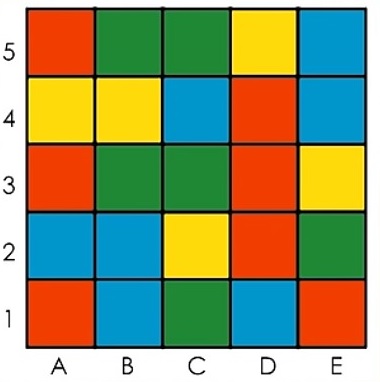
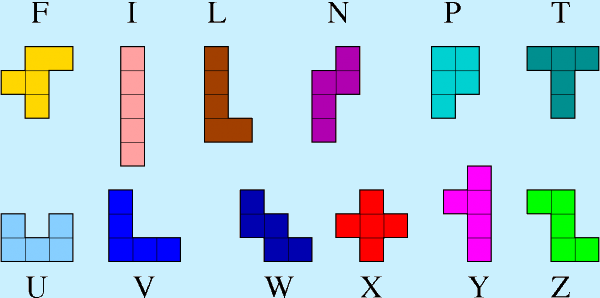
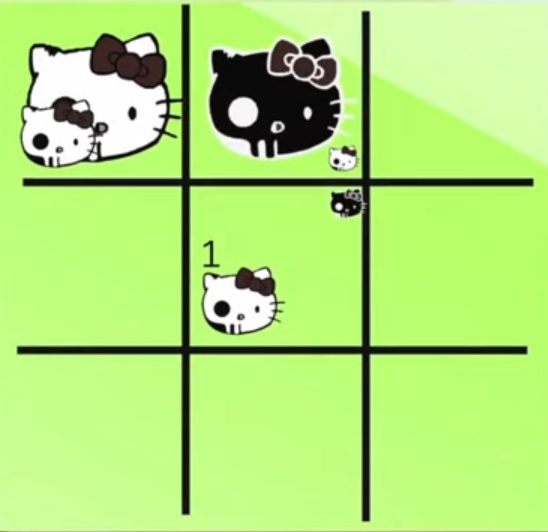
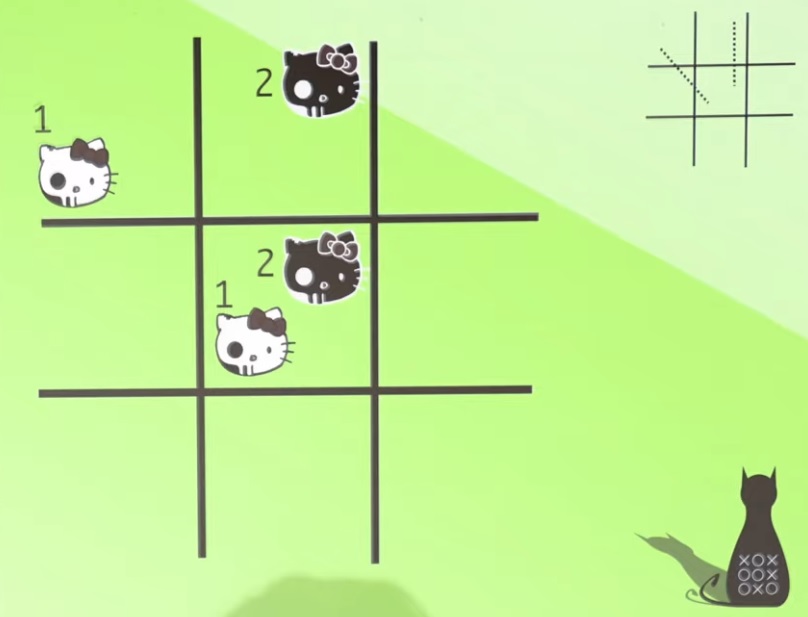
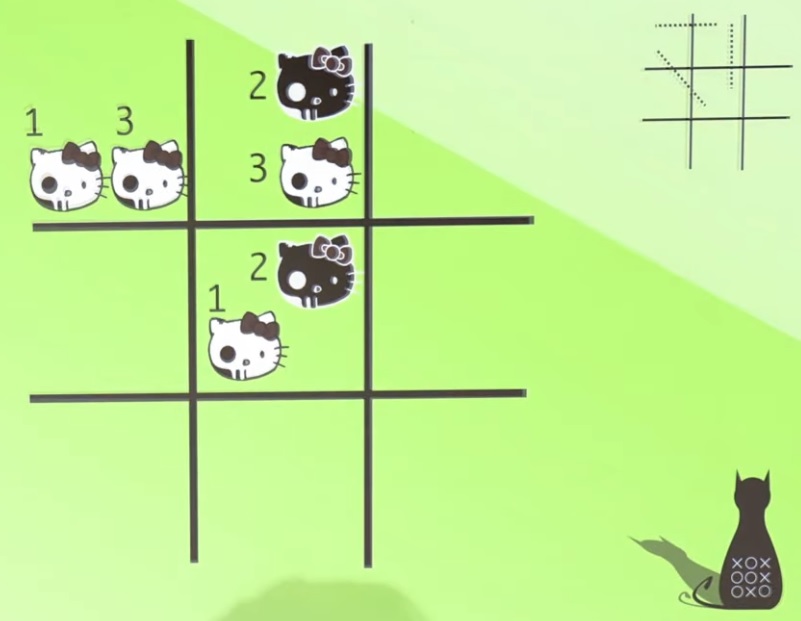
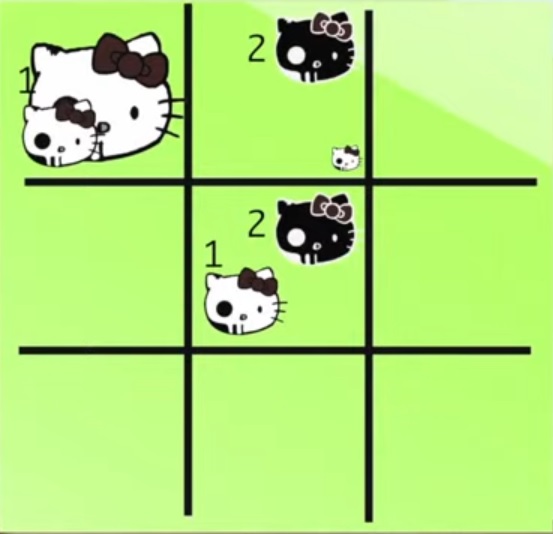
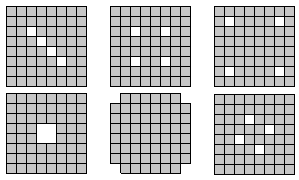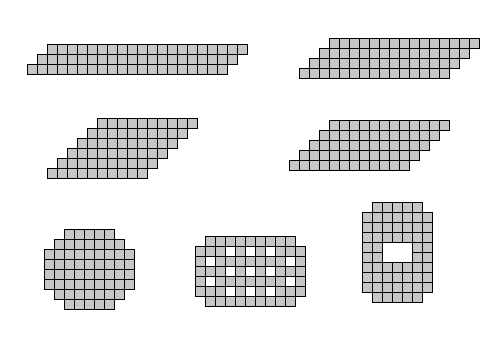. 200°/ Les sabliers :
Vous disposez de deux sabliers : un gros de 7 minutes et un petit de 4 minutes.
Comment faire pour chronométrer 9 minutes ?
. 201°/ Les macarons :
Jean, Paul et Guillaume font partie d’un club très exclusif : ils en sont les trois seuls membres.
Ils arborent toujours un macaron spécial proclamant leur appartenance à leur club. Vous savez identifier leur macaron, mais vous n’avez jamais rencontré aucun des trois.
Cependant, vous savez que Jean et Paul mentent toujours, mais que Guillaume dit toujours la vérité.
Un jour, vous croisez sur la rue une personne portant le macaron du club.
Adressez-lui une seule question de trois mots, à laquelle elle peut répondre par un ‘oui’ ou par un ‘non’ et qui vous permettra de déterminer si la personne est Jean.
[Deux mots unis par un trait peuvent être comptés comme un seul.]
. 202°/ Les neufs loups :
 |
Neuf loups se retrouvent dans une enceinte carrée au jardin zoologique. Vous devez y ajouter deux nouvelles enceintes carrées de telle sorte qu’il sera possible d’isoler chaque loup dans sa propre enceinte.
Comment faire ? |
. 203°/ Les dix brebis :
 |
Dix brebis se retrouvent dans une enceinte circulaire au jardin zoologique. Vous devez y ajouter trois nouvelles enceintes circulaires de telle sorte qu’il sera possible d’isoler chaque brebis dans sa propre enceinte.
Comment faire ? |
. 204°/ Les trois boîtes de fruits :
Chez votre marchand de fruits, il y a trois boîtes fermées sur une table.

Votre marchand vous assure qu’aucune étiquette n’est bien placée, et vous propose un jeu.
Il choisira et vous montrera un seul fruit d’une seule boîte à votre choix, et parie que vous ne pouvez pas replacer correctement les étiquettes sur la base de cette maigre information.
Pouvez-vous gagner la gageure ?
. 205°/ Les cinq chapeaux :
 |
Trois personnes très intelligentes sont placées l’une derrière l’autre, de telle sorte que la première devant ne voit aucune des deux autres, la deuxième ne voit que la première, et la troisième voit les deux autres. Chaque personne ne peut pas voir son propre chapeau. |
 |
Les trois ferment les yeux pendant que quelqu’un leur met chacune un chapeau sur la tête ; les chapeaux sont choisis d’un lot de trois jaunes et deux rouges. |
 |
Les trois personnes ouvrent les yeux, et on demande à la troisième si elle connaît la couleur de son chapeau ; elle répond ‘non.’
On pose ensuite la même question à la deuxième, et elle répond également ‘non.’
Finalement, on pose la même question à la première, qui répond ‘oui.’
Quelle est la couleur du chapeau de la première personne ? |
Dans le même style : Les prisonniers :
Un roi décide de gracier l’un de ces trois prisonniers. Pour savoir lequel libérer il les soumet à l’épreuve suivante :
On place les trois prisonniers en triangle. Dans un sac on place 3 boules rouges et 2 boules noires.
On mélange le tout puis on place une boule tirée au hasard sur la tête des prisonniers de sortes que chaque prisonnier voit la boule posée sur la tête des deux autres mais pas celle qui est sur sa tête.
Le roi libérera celui qui devinera la couleur de la boule qui est sur sa tête, tuera celui qui donnera une mauvaise réponse et remettra en prison celui qui ne se prononcera pas. Il interroge les prisonniers dans l’ordre fixé.
Les prisonniers n°1 et 2 ne se prononcent pas.
Le prisonnier n°3 qui voit une boule rouge sur la tête des deux autres peut alors facilement deviner la couleur de la boule sur sa tête.
. 206°/ La suite :
Quel est le prochain terme de cette suite ?
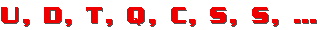
. 207°/ Une autre suite :
Ce problème s’adresse aux personnes qui comprennent l’anglais.
What is the next term in the following sequence ?

. 208°/ Une dernière suite :
Quel est le prochain terme de cette suite ?

. 209°/ Le téléphone cryptique :
Lors d’une soirée mondaine, on vous présente une personne qui pique votre intérêt. Après une discussion passionnante, vous convenez de vous revoir, et vous lui donnez votre numéro de téléphone.
En retour, elle fait de même, mais cryptiquement.
« Vous connaîtrez mon numéro de téléphone lorsque vous aurez rempli les blancs dans la phrase qui suit ; mon numéro est constitué, dans l’ordre, des dix chiffres insérés. »
(N.B.: en Amérique du Nord, les numéros de téléphone comportent trois chiffres
pour l’indicatif régional et sept chiffres pour le poste, ainsi: 555-234-6789.)
Voici la phrase cryptique :
Dans cette phrase, le nombre d’occurrences de 0 est __ , de 1 est __ , de 2 est __ , de 3 est __ ,
de 4 est __ , de 5 est __ , de 6 est __ , de 7 est __ , de 8 est __ , et de 9 est __ .
Quel est son numéro de téléphone ?
. 210°/ Les huit galettes :
Albert se rendant au château, rencontre en chemin Belmondo. Ils décident de continuer leur chemin ensemble.
A l’heure du déjeuner, Albert sort de sa besace cinq galettes de blé, et Belmondo trois galettes.
Albert propose, pour sceller cette amitié nouvelle, de partager la totalité du repas entre eux deux. Arrive alors un vieillard à l’air fatigué. Les deux hommes décident d’un commun accord de diviser équitablement leur repas à trois.
Une fois le déjeuner terminé, le vieillard se lève, lance huit pièces d’or sur la table, remercie les deux hommes, et s’en va.
Albert dit alors : « Puisque j’ai apporté 5 galettes et toi 3, je dois prendre 5 pièces, et toi 3. »
Belmondo répond : « Puisqu’on devait partager le repas à deux, on doit partager la somme en deux, soit 4 pièces chacun. »
Ils décident, pour résoudre ce dilemme, de le soumettre au souverain du château.
Celui-ci, une fois au courant du problème, réfléchit quelques minutes et leur dit : « Si vous recherchez le juste partage, alors Albert doit recevoir 7 pièces, et Belmondo 1 pièce. »
Pourquoi ?
. 211°/ Les 100 déclarations :
Sur une feuille de papier, on a 100 déclarations.
La déclaration 1 dit « Il y a exactement 1 déclaration fausse sur cette feuille de papier », La déclaration 2 dit « Il y a exactement 2 déclarations fausses sur cette feuille de papier », ainsi de suite jusqu’à 100.
Quelles sont les déclarations vraies, et quelles sont celles qui sont fausses ?
. 212°/ Les moines malades :
Dans une abbaye de moines où chacun a fait le vœu solennel de silence total, une maladie se déclare. Les moines sont au courant de cette maladie qui se caractérise par l’apparition d’un point noir au milieu du front.
Ils ont appris que cette maladie est contagieuse et que chaque jour un nouveau moine en sera atteint.
Ils n’ont à leur disposition aucun objet réfléchissant. Leur vœu de silence est extrêmement sévère : non seulement ne peuvent-ils pas parler, mais ils n’ont pas le droit de communiquer par écrit ni même par signes.
On leur demande de quitter le monastère une fois qu’ils sont atteints de la maladie pour ne pas aggraver l’épidémie.
Le premier jour, un moine quitte le monastère ; il est atteint de la maladie et il le sait.
Le lendemain, un autre moine quitte le monastère sachant aussi qu’il est atteint de la maladie.
Et ainsi de suite, à chaque jour, jusqu’à ce que l’abbaye soit vide…
Comment savent-ils qu’ils sont malades ?
. 213°/ Les cent souris :
Si 3 chats peuvent attraper 3 souris en 3 minutes…
…combien de chats sont nécessaires pour attraper 100 souris en 100 minutes ?
. 214°/ Les quatre paquets :
Luc travaille dans un entrepôt à étiqueter des paquets qui sont par la suite expédiés aux clients.
Un jour qu’il reçoit quatre commandes à étiqueter en même temps, il échappe toutes ses étiquettes par terre. Il les ramasse et les colle au hasard sur les paquets.
Quelle est la probabilité qu’exactement trois des quatre paquets soient correctement étiquetés ?
. 215°/ La poste blindée :
 C’est un pays imaginaire où les habitants ne peuvent communiquer que par la Poste. Malheureusement, les postiers de ce pays sont tous, sans exception, des voleurs systématiques.
C’est un pays imaginaire où les habitants ne peuvent communiquer que par la Poste. Malheureusement, les postiers de ce pays sont tous, sans exception, des voleurs systématiques.
Pour protéger ses communications, chaque habitant dispose d’une boîte blindée, de son propre cadenas et d’une unique clé qui, seule, peut ouvrir son cadenas. Les lettres sont d’abord placées dans une boîte blindée, qui est par la suite cadenassée puis expédiée.
Les postiers livrent intactes les boîtes cadenassées. Mais si par malheur une boîte non cadenassée leur passe entre les mains, ils en volent le contenu. Et si, comble de malheur, on oublie de verrouiller son cadenas, ils le volent aussi !
Il est donc absolument nécessaire d’utiliser une boîte cadenassée pour expédier du courrier dans ce pays, et tout courrier doit nécessairement passer par la Poste.
 Deux habitants de ce pays, Pierre et Paul, désirent s’échanger du courrier. Ils ne veulent pas que des yeux indiscrets puissent lire leur courrier, alors pas question de tout simplement écrire le message sur la boîte ! Vu qu’il n’y a qu’une seule clé pour chaque cadenas et qu’ils n’ont pas le loisir de se rencontrer pour s’échanger leurs clés respectives…
Deux habitants de ce pays, Pierre et Paul, désirent s’échanger du courrier. Ils ne veulent pas que des yeux indiscrets puissent lire leur courrier, alors pas question de tout simplement écrire le message sur la boîte ! Vu qu’il n’y a qu’une seule clé pour chaque cadenas et qu’ils n’ont pas le loisir de se rencontrer pour s’échanger leurs clés respectives…
…comment Pierre peut-il expédier une lettre à Paul ?
. 216°/ Les deux cordes :
Voici deux cordes cirées (leur longueur exacte n’a pas d’importance).

Chacune des cordes brûlera complètement en une heure exactement.
Cependant, elles brûlent à un rythme inégal.
Ceci veut dire que vous ne pouvez pas y faire des marques à la moitié, au quart, etc., pour ainsi mesurer le temps écoulé.
Vous voulez chronométrer 45 minutes au moyen de ces deux cordes.
Vous disposez d’allumettes, c’est tout.
Comment faire ?
. 217°/ Deux fois l’âge :
Un homme dit à son fils :
« J’ai deux fois l’âge que tu avais quand j’avais l’âge que tu as. »
Sachant que le père a entre 73 et 79 ans…
…quel est l’âge du fils ?
. 218°/ Trois fois l’âge :
J’ai trois fois l’âge que vous aviez quand j’avais l’âge que vous avez.
Quand vous aurez l’âge que j’ai, nous aurons, à nous deux, 98 ans.
Quel âge ai-je donc ?
. 219°/ Le fusil et la panthère :
Tu es toute seule / tout seul dans le désert.
À ta disposition : un fusil avec deux cartouches c’est tout.
Au loin, tu vois une panthère qui passe.
Tu as une folle envie de fumer.
Comment s’y prendre ?
. 220°/ Les couples à la plage :
Sur une plage, cinq couples passent l’après-midi ensemble.
| Barbara |
Gisèle |
Nadine |
Jacques |
Rémi |
| Geneviève |
Isabelle |
Alexandre |
Nicolas |
Thomas |
À un moment donné, on constate que :
1°/ La femme de Rémi fait une partie de pétanque avec le mari de Geneviève.
2°/ Barbara joue au ping-pong avec son mari Nicolas.
3°/ Jacques et Nadine font la sieste.
4°/ Thomas et Gisèle s’amusent aux fléchettes.
…et on sait que…
5°/ Nadine n’est pas la femme de Thomas.
Qui est la femme de Jacques ?
. 221°/ Les bateaux et la bouée :
Deux bateaux, identiques sauf pour la couleur un est bleu et l’autre rouge sont amarrés au même quai sur une rivière. Leurs capitaines reçoivent l’ordre de naviguer à plein régime : le rouge en amont et le bleu en aval.
Le courant de la rivière est constant à 5 km/h. Sur l’eau calme, les bateaux peuvent atteindre 12 km/h à plein régime.

Les deux bateaux quittent le quai au même moment ; à ce même moment, une bouée qui était sur le quai tombe à l’eau.

Une heure plus tard, les capitaines reçoivent l’ordre de faire demi-tour et de revenir en sens inverse, toujours à plein régime.

Quel bateau atteindra la bouée en premier ?
. 222°/ Marie et le train :
Marie marche dans un tunnel. Arrivée aux 3/8 du chemin, elle entend le sifflet d’un train venant derrière elle.

D’après son expérience, elle sait que le train roule toujours à 60 km/h sur cette portion de la voie.
Elle fait un calcul mental rapide : elle peut éviter le train de justesse…
…si elle court vers l’entrée du tunnel…

…ou si elle court vers la sortie…

À quelle vitesse Marie court-elle ?
. 223°/ Monsieur et Madame Duziel :
Monsieur et Madame Duziel ont cinq filles, comment s’appellent-elles ?
. 224°/ Paris-Caen-Paris :
Pierre doit faire un trajet aller-retour Paris ? Caen ? Paris.
Il fait le trajet aller (Paris ? Caen) à la vitesse moyenne de seulement 60km/h, à cause de la lourde circulation.

À quelle vitesse doit-il rouler au retour (Caen ? Paris) pour que sa
vitesse moyenne globale (aller-retour) soit de 120 km/h ?
. 225°/ Les chapeaux blancs :
Les trois sont placés de telle sorte que chacun peut voir les deux autres. On leur explique qu’on va leur bander les yeux et leur poser un chapeau blanc ou noir sur la tête. En retirant le bandeau, si l’individu aperçoit au moins un chapeau blanc sur la tête d’un autre participant, il doit lever la main.
Le but du jeu est évidemment de deviner la couleur de son propre chapeau (que le participant ne peut voir d’aucune façon).
On bande donc les yeux des trois participants et on dépose un chapeau blanc sur la tête de chacun. On enlève les bandeaux.
Après quelques instants: 
Comment 3 a-t-il raisonné pour arriver à cette conclusion ?
P.S.: Si le chapeau de 3 avait été noir, les trois auraient levé la main de toute façon !
. 226°/ Le train et les deux wagons :
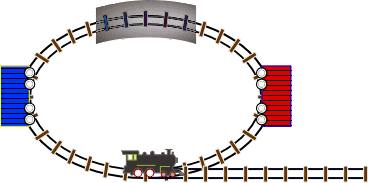
Une voie ferrée de forme ovale, avec une voie d’évitement sans issue.
Une locomotive et deux wagons un rouge et un bleu.
Un tunnel dans lequel seule la locomotive peut passer (les deux wagons sont trop haut).
La locomotive peut pousser un ou deux wagons à la fois, mais ne peut en tirer qu’un seul à la fois.
Comment interchanger les wagons, tout en remettant la locomotive à sa position initiale ?
. 227°/ La suite ascen-descendante :
Quel est le prochain terme de la suite suivante ?
6, 25, 64, 81, 32, __
. 228°/ Le rébus en A :

Quel est le sens de cette inscription ?
. 229°/ La suite mélangée :
A Y 3 D V 6 G S 9 J ? 12
Quel est le symbole manquant ?
. 230°/ Le verger le retour ! :
Un jardinier veut planter 15 pommiers.

Il veut faire 6 rangées de 5 arbres chacune.
Comment faire ?
. 231°/ Le tapis magique :
Descartes a un salon mesurant 13 x 5 unités (65 unités carrées). Il veut installer un tapis neuf qu’il a reçu en cadeau, mais qui mesure 8 x 8 unités (64 unités carrées). Comme il ne veut pas acheter un deuxième tapis et que le marchand ne peut pas lui vendre une pièce d’une unité carrée parce que ce modèle n’est plus disponible, il décide de se débrouiller autrement.
Il rentre donc chez lui, puis il découpe son tapis de 8 x 8 ainsi:
(On a coloré les morceaux pour les besoin de ce problème Descartes n’aurait jamais posé un tapis si bigarré !)
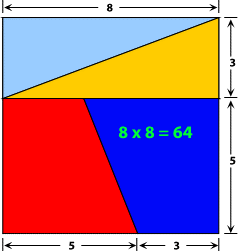
Ensuite, il dispose les morceaux sur son parquet de salon ainsi :
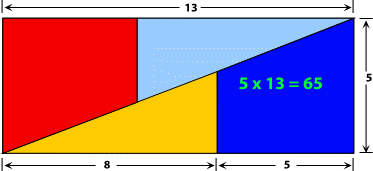
Comme par magie, le tapis reconstitué recouvre tout le parquet !
Comment est-ce possible ?
. 232°/ Le rébus en G :

Quel est le sens de cette inscription ?
. 233°/ Le garde du château :
Pour entrer dans le château, il est nécessaire de connaître le mot de passe. Alors vous observez et écoutez les gens qui se présentent à la porte. Un enfant arrive ; le garde lui dit « 5 », l’enfant répond « 4 » et le garde le laisse entrer. Une femme se présente ; le garde lui dit « 6 », elle répond « 3 » et passe. Un homme paraît ; le garde lui dit « 4 », l’homme répond « 6 » et entre. C’est votre tour. Le garde vous dit « 7 ». Que répondez-vous ?
. 234°/ Qu’est-ce que c’est ? :
Le pauvre l’a.
Le riche en a besoin.
Les morts le mangent, mais si des vivants le mangent, ils en meurent.
C’est meilleur que le paradis.
C’est pire que l’enfer.
Qu’est-ce que c’est ?
. 235°/ Les cent moines :
Dans un monastère isolé d’Italie, vivent 100 moines. Ils ont fait vœu de silence et ne communiquent jamais entre eux de quelque manière que ce soit. Donc, les moines n’ont pas le droit de se parler, mais une prière commune a lieu tous les matins, et c’est le seul moment de la journée où ils se voient.
A la prière du lundi matin, le patriarche fait une annonce à tous les moines : une malédiction a frapper le monastère cette nuit et les moines maudits auront sur le front une petite marque rouge.
Il y a au moins un malade.
Les moines ne possèdent pas de miroir ni de surface réfléchissante de quelque sorte que ce soit.
Si un moine est absolument sûr d’être maudits, il se suicide la nuit même.
Du lundi au dimanche, rien ne se passe, mais le lundi suivant au matin, on découvre que tous les moines maudits se sont suicidés pendant la nuit.
Combien y avait-il de atteints ?
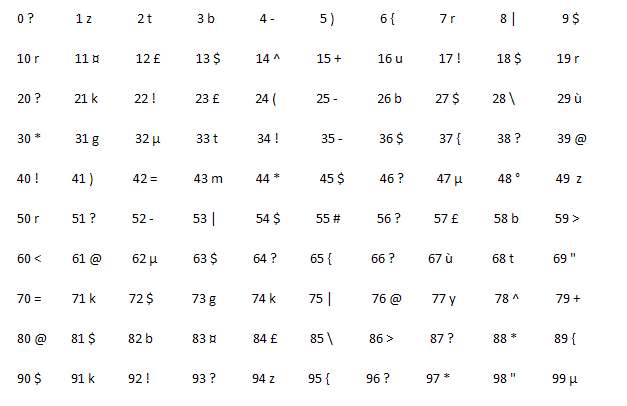
. 236°/ Le septième chiffre :

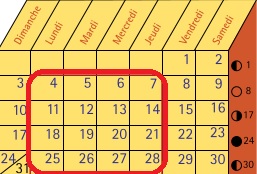
. 237°/ La carte bigarrée :
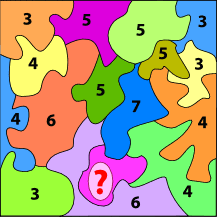
. 238°/ Les cinq figures :
Chacune des deux figures qui précèdent est divisée en quatre parties identiques.
Pouvez-vous diviser ce carré en cinq parties identiques ?

. 239°/ Les trois agents secrets :
Trois agents secrets sont accusés d’être des agents doubles.
Voici leurs témoignages :



Les agents doubles mentent toujours.
Les autres agents disent toujours la vérité.
Il n’y a qu’un seul agent double parmi les trois.
Qui est l’agent double ?
. 240°/ Paris-Clamart-Versailles :
Un retraité de la société des chemins de fer, voulant se remémorer le bon vieux temps, aime à prendre le train chaque jour. En tant que retraité, il n’a pas besoin de billet, et peut voyager gratuitement.
Chaque jour, il se rend donc à la gare de Clamart qui est située entre Paris et Versailles. Cette gare n’est desservie que par une ligne reliant Paris à Versailles dans les deux sens, c’est-à-dire qu’il peut prendre soit un train partant de Paris, et ce toutes les 15 minutes, soit un autre partant de Versailles toutes les 15 minutes. Chaque train roule sur sa propre voie et les deux voies sont parallèles. Chaque train démarre des terminus Paris et Versailles exactement aux quarts d’heure (à xh00, xh15, xh30 et xh45…).
Arrivé à la gare, à une heure aléatoire, il prend le premier train qui se présente et bavarde avec le chauffeur. Puis, arrivé au terminus, c’est à dire à Paris où à Versailles, il descend et reprend un train dans l’autre sens, pour rentrer chez lui.
Or, il apparaît que le vieux monsieur arrive 2 fois sur 3 à Versailles, et seulement 1 fois sur 3 à Paris, ce qui est étrange puisque les trains passent exactement à la même fréquence une fois toutes les 15 minutes et qu’il prend toujours le premier train se présentant en gare. Il y a autant de voyages Paris-Versailles que Versailles-Paris, les trajets sont parfaitement symétriques, etc…
Quelle en est l’explication ?
. 241°/ Le cheval et l’oiseau :

Pouvez-vous démontrer cela ?
. 242°/ Bacchus et Silène :
Bacchus ayant vu Silène
Auprès de sa cuve endormi
Se mit à boire sans gêne
Au dépens de son ami.
Ce jeu dura pendant le triple du cinquième
Du temps qu’à boire seul Silène eut employé.
Il s’éveille bientôt, et son chagrin extrême
Dans le reste du vin est aussitôt noyé.
S’il eut bu près de Bacchus même
Ils auraient, suivant le problème,
Achevé 6 heures plus tôt :
Alors Bacchus eut eu, pour son écot
Deux tiers de ce qu’à l’autre, il laisse.
Ce qui maintenant m’intéresse
Est de savoir exactement
Le temps qu’à chaque drôle il faut séparément
Pour vider la cuve entière
Sans le secours de son digne confrère.
. 243°/ Les quatre chapeaux :
Dans un bistro, 4 mecs se croient plus forts que le patron et lui lancent un défi.
« Proposez-nous n’importe quel test de raisonnement, et nous parions chacun 50 dollars que nous trouverons la réponse ! »
Le patron réfléchit un moment et répond qu’il accepte le pari ; voici ce qu’il leur dit.
« Je vais vous placer en ligne, et vous n’aurez pas le droit de regarder ailleurs que droit devant.

Entre A et les trois autres, je place un paravent opaque.
Ainsi, A ne voit aucun des trois autres, B non plus, C voit B seulement, et D voit B et C.
Fermez les yeux pendant que je dépose un chapeau sur la tête de chacun, à partir d’un stock de quatre chapeaux : deux noirs et deux blancs.
Pour gagner le pari, il suffit que l’un d’entre vous dise correctement la couleur de son propre chapeau.
Vous n’avez pas le droit de communiquer entre vous. À la première erreur, le pari est perdu et je rafle les 200 dollars !
Ouvrez les yeux et je vous accorde deux minutes allez-y ! »
Après 1 minute un des quatre parle et les mecs gagnent le pari…
Question n°1 : Quel est ce mec ?
Question n°2 : Pourquoi est-il certain de la couleur de son chapeau ?
. 244°/ Les trois pièces de monnaie :
Il y a trois pièces de monnaie dans un sac fermé.
- Une pièce est normale, avec un côté ‘face’ et l’autre côté ‘pile’.
- Une pièce est anormale, avec deux côtés ‘pile’.
- Une pièce est anormale, avec deux côtés ‘face’.
On agite le sac,
on y plonge la main sans regarder,
on choisit une pièce au hasard,
on la place sur la table sans en inspecter l’autre côté.
La pièce montre un ‘face’.
Quelle est la probabilité que le côté caché de cette pièce soit un ‘pile’ ?
. 245°/ Les cent déclarations :
Sur une feuille de papier, cent déclarations sont inscrites.
La première dit : « Sur cette feuille il n’y a qu’une seule fausse déclaration. »
La seconde dit : « Sur cette feuille il y a deux et seulement deux fausses déclarations. »
La troisième dit : « Sur cette feuille il y a trois et seulement trois fausses déclarations. »
et ainsi de suite jusqu’à…
… la 100e qui dit : « Sur cette feuille il y a cent et seulement cent fausses déclarations. »
Combien de déclarations sont vraies sur cette feuille ? Combien sont fausses ? et pourquoi ?
. 246°/ Les deux véhicules :
Le véhicule A roule à 60 km/h et dépasse le véhicule B qui roule à 45 km/h.
Pendant combien de temps le véhicule A doit-il rouler pour pouvoir s’arrêter pendant 5 minutes sans être doublé par le véhicule B (qui continue à vitesse constante) ?
. 247°/ Les deux mâts :
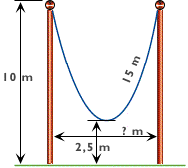
Deux mâts à drapeau mesurent 10 mètres de hauteur. Un câble de 15 mètres les relie, à partir de leurs extrémités supérieures. À son point le plus bas, le câble est à 2,5 mètres du sol.
Quelle distance sépare les deux mâts ?
. 248°/ Le carré parfait :

Comment faire ?
. 249°/ Le vinaigre :
:
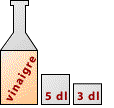
Vous êtes en camping et vous voulez confectionner votre fameuse vinaigrette pour la petite salade. La recette exige 4 décilitres de vinaigre. Mais voilà que vous n’avez pas grand-chose sous la main. Vous ne disposez que de deux contenants non gradués : un de 5 décilitres, l’autre de 3 décilitres, et comme vous êtes un grand maniaque, vous voulez que les 4 décilitres soient contenus dans un seul récipient.
Comment mesurer 4 décilitres ?
. 250°/ Les trois triplets :
|
Vous devez construire un nombre à neuf chiffres, composé de trois triplets de trois chiffres chacun.
|

|
|
Le nombre correspondant au premier triplet est égal au tiers du nombre correspondant au dernier triplet.
|
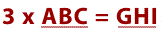
|
|
Le nombre correspondant au triplet du milieu est obtenu en soustrayant le premier triplet du troisième.
|

|
|
Chaque chiffre de 1 à 9 est utilisé une et une seule fois.
|

|
Quel est le nombre recherché ?
. 251°/ La mouche et la boîte :
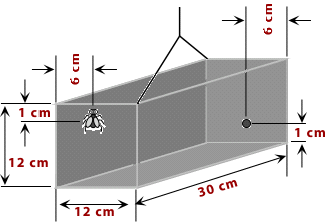
Une boîte mesurant 12 cm x 12 cm x 30 cm est suspendue du plafond au moyen d’une ficelle fixée à deux coins. Une mouche est au milieu d’un bout avant de la boîte, sur la paroi extérieure, à 1 cm du haut. Elle veut se rendre jusqu’au point situé au milieu de l’autre bout arrière, à 1 cm du bas. La boîte est complètement fermée: la mouche doit donc marcher sur l’une ou l’autre des six parois extérieures elle ne peut pas entrer dans la boîte.
Quelle est la distance la plus courte qu’elle doit parcourir pour atteindre le point ?
. 252°/ Les neuf cigarettes :
Vous êtes l’agent secret James Lesmath et vous êtes à la recherche d’un petit microfilm d’une valeur inestimable.
Vous savez que le microfilm est dissimulé dans une des neuf cigarettes d’un paquet de cigarettes.
Vous savez que toutes les cigarettes ont exactement le même poids sauf celle qui contient le microfilm, qui est légèrement plus lourde.
Pour éviter de vous faire repérer, au lieu de voler le paquet entier, vous décider de ne prendre que la cigarette contenant le microfilm ! Vous remarquez une balance à fléaux à côté du paquet de cigarettes (oui c’est possible ! !).
Malheureusement, le temps presse et vous ne pouvez effectuer que deux pesées avant de vous faire repérer.
Quelle séquence de 2 pesées vous permettra d’identifier la cigarette contenant le microfilm ?
Variante rapide :
On présente 8 billes identiques à Jean. Une de ces 8 billes pèse 1 gramme de plus que les autres. Avec les mains, il est donc impossible de déterminer la plus lourde des billes.
Avec seulement 2 pesées, Jean a réussi à déterminer la plus lourde des billes.
Comment a-t-il fait ?
. 253°/ La suite infernale :
 Quelle est la prochaine ligne de cette suite ?
Quelle est la prochaine ligne de cette suite ?
. 254°/ Les dix sacs d’or :
:
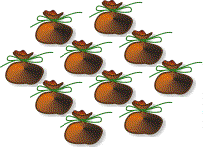
Devant vous se trouvent dix sacs, contenant chacun une cinquantaine de pièces d’or sans que vous ne connaissiez le nombre exact.
9 sacs contiennent des pièces de 5 gr et le dernier sac des pièces de 6 gr.
On vous offre le sac contenant ces pièces de 6 gr, pour autant que vous puissiez l’identifier au moyen d’une seule pesée faite sur une balance électronique qui vous donnera la masse exacte.
Comment faire ?
. 255°/ Les seize points :

:
Pouvez-vous relier ces seize points au moyen de six lignes droites tracées sans lever votre crayon du papier ?
. 256°/ Les six passagers :
Trois cannibales et trois missionnaires doivent traverser une rivière.
Il y a une barque disponible, mais elle ne peut permettre l’embarquement que de deux personnes à la fois.
Afin d’éviter le pire (…) il faut absolument faire en sorte que le nombre de cannibales ne dépasse jamais le nombre de missionnaires sur une rive ou l’autre !
Notez que lorsque la barque est accostée à une rive, la ou les personnes qui y prennent place comptent dans le nombre total sur la rive en question…
De plus la barque ne peut pas traverser toute seule.
Comment traverser ces six passagers sains et saufs ?
. 257°/ Les deux trains :
Le train 1 quitte la ville A sur une voie ferrée parfaitement rectiligne et sans dénivelé et, tout en maintenant une vitesse de croisière d’exactement 45 km/h, se dirige, sans arrêt, vers la ville B qui se trouve à l’est.
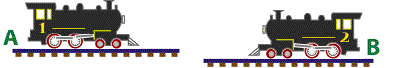
Sur une voie rigoureusement parallèle à celle empruntée par l’autre train, le train 2 quitte la ville B au même moment, maintient une vitesse de croisière d’exactement 60 km/h et se dirige vers la ville A qui se trouve à l’ouest.
Pour simplifier les calculs, on peut négliger le temps nécessaire pour l’accélération de chacun des deux trains jusqu’à sa vitesse de croisière, ainsi on supposera qu’ils démarrent instantanément à 45 km/h ou 60 km/h, selon le cas…
On suppose aussi qu’il n’y a pas de vent ce jour-là.
Lequel des deux trains sera le plus près de la ville A lorsqu’ils se rencontreront ?
. 258°/ Sacrée soirée :
André avait 2 sorties prévues dans la même soirée. Il s’est tout d’abord rendu Ginette, mais n’est resté que 30 secondes, juste le temps d’avaler un whisky on the rocks (un whisky avec des glaçons pour les buveurs d’eau), puis s’est excusé pour se rendre chez Serge à sa deuxième soirée.
Malheureusement, certains des invités qui ont continué la fête chez Ginette sont morts empoisonnés. Après enquête de la police, et grâce à l’analyse des verres de la fête il est certain que les whiskys on the rocks étaient empoisonnés. Cependant André lui, est toujours vivant ! ! !
Pourquoi André n’est-il pas mort empoisonné ?
. 259°/ Le neuf en six :
Il y a au moins trois façons de transformer IX en 6, en utilisant un seul trait de crayon, sans lever le crayon du papier…
Quelles sont ces trois façons ?
. 260°/ La spirale infernale :
À 4 h du matin, un 15 octobre, Vanessa se promène près de son domicile à Zürich, en Suisse. Soudainement, elle aperçoit un vaisseau en forme de disque argenté dans le ciel. L’OVNI atterrit et un extra-terrestre en émerge.
« Nous sommes des Pléiades, dans la constellation du Taureau, à quelque 430 années-lumière de votre planète, » lui dit l’extra-terrestre. « Nous désirons mesurer l’intelligence de votre espèce ; à cet effet, nous vous donnons une mission à accomplir. Acceptez-vous de relever le défi ? »
Vanessa, désireuse de lui montrer que son espèce peut faire preuve d’une intelligence équivalente à celle de cette race venue des Pléiades, répond, « Oui, bien sûr ! »
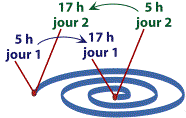
L’extra-terrestre donne ses instructions à Vanessa, puis la transporte vers un tube transparent en forme de spirale, long d’un kilomètre et dont le diamètre est tellement réduit qu’elle doit y ramper.
Elle commence son périple à 5 h et rampe jusqu’à l’autre bout de la spirale, qu’elle atteint à 17 h du même jour, exactement 12 heures plus tard. Pendant son périple, elle avance à des vitesses variables et fait des pauses de temps en temps afin de se reposer. Elle se nourrit à partir d’une musette qu’elle porte à sa ceinture.
Elle refait ses forces en dormant à l’autre bout de la spirale, puis entreprend son voyage de retour le lendemain matin à 5 h. Tout comme le jour d’avant, elle se repose de temps en temps et arrête pour casser la croûte. Elle ressort toute épuisée de la spirale 12 heures plus tard, à 17 h.
« Vous avez accompli votre mission, » lui dit l’extra-terrestre. « Maintenant, voici la question pour mesurer votre intelligence. »
« Quelles sont les chances qu’il y ait un point de la spirale (autre que les points de début et de fin) que vous avez atteint à exactement la même heure à chacun des deux jours ?«
. 261°/ Le marchand de tapis :
Vous avez acheté une moquette de 10 m. sur 10 m pour votre salon. En tentant de la mettre en place, vous vous apercevez de votre erreur : votre salon mesure plutôt 9 m sur 12 m.

Vous retournez chez votre marchand de tapis et, fin géomètre qu’il est, il vous vend une bande supplémentaire de 1 m sur 8 m en vous assurant qu’en pratiquant une seule coupe dans la moquette d’origine, vous pourrez maintenant couvrir le parquet parfaitement.
Comment pratiquer cette coupe ?
. 262°/ L’oiseau loco :
Le train 1 quitte la ville A sur une voie ferrée parfaitement rectiligne et planche et, tout en maintenant une vitesse de croisière d’exactement 30 km/h, se dirige sans arrêt vers la ville B qui se trouve à 120 km à l’est.
Sur une voie rigoureusement parallèle à celle empruntée par l’autre train, le train 2 quitte la ville B au même moment, maintient une vitesse de croisière d’exactement 30 km/h et se dirige vers la ville A qui se trouve à l’ouest.
Pour simplifier les calculs, on peut négliger le temps nécessaire pour l’accélération de chacun des deux trains jusqu’à sa vitesse de croisière ainsi, on supposera qu’ils démarrent instantanément à 30 km/h.
On suppose aussi qu’il n’y a pas de vent ce jour-là.

Pendant ce temps, un oiseau part de la locomotive A pour se diriger vers la loco B. Rendu à la loco B, il change de direction et retourne vers la loco A. Il répète la même chose jusqu’au moment où les deux locomotives se croisent. L’oiseau vole à 100 km/h et, pour simplifier les calculs, on supposera qu’il démarre instantanément à 100 km/h et qu’il met un temps nul pour changer de direction.
Quelle distance l’oiseau parcourra-t-il entre le moment où les locomotives partent de leurs villes respectives et le moment où elles se croisent ?
. 263°/ Le panier d’œufs:
 Un panier d’œufs coûte 1,10 $.
Un panier d’œufs coûte 1,10 $.
Le panier seul vaut 1 $ de plus que les œufs.
 Combien coûtent les œufs?
Combien coûtent les œufs?
. 264°/ Le retour de bouteilles :
Si une bouteille pleine d’une boisson quelconque coûte 30 cents, et si le contenu coûte 20 cents de plus que la bouteille vide qui est consignée, combien de bouteilles vides doit-on retourner chez le marchand pour obtenir une bouteille pleine ?
. 265°/ Le sultan, sa fille et le prétendant :
Un sultan souhaite se débarrasser du prétendant de sa fille, mais n’ose pas le faire exécuter arbitrairement. Alors, il lui propose un jeu de hasard auquel il ne peut se soustraire de peur de passer pour un couard aux yeux de sa belle.
Devant la cour, le sultan chiffonne deux bouts de papier et les introduit dans une urne. Il explique que sur un papier il est écrit « Vivre » et sur l’autre « Mourir. »
Le sultan demande à sa fille de tirer un papier de l’urne, étant entendu que le prétendant vivra ou mourra selon le message qu’on y lira.
Or, la fille du sultan est vraiment amoureuse du prétendant. De plus, elle sait que le sultan a triché, car il a inscrit « Mourir » sur les deux bouts de papier !
Comment la fille du sultan peut-elle sauver la vie de son fiancé ?
. 266°/ Les boules de pétanque :
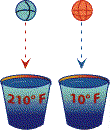
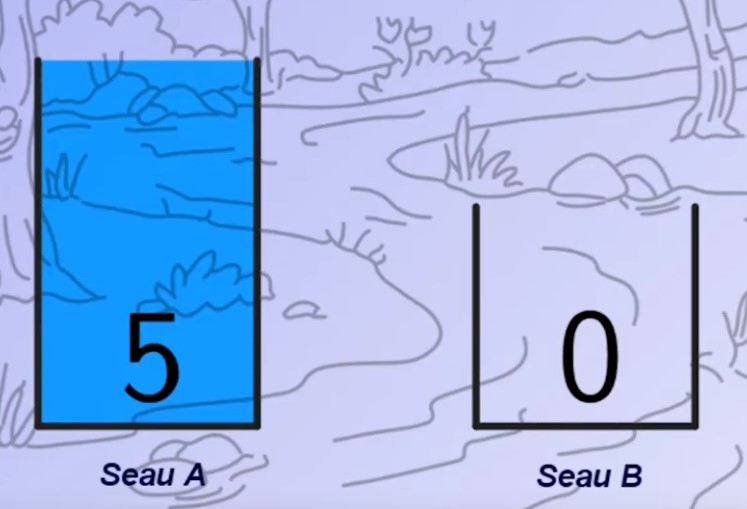
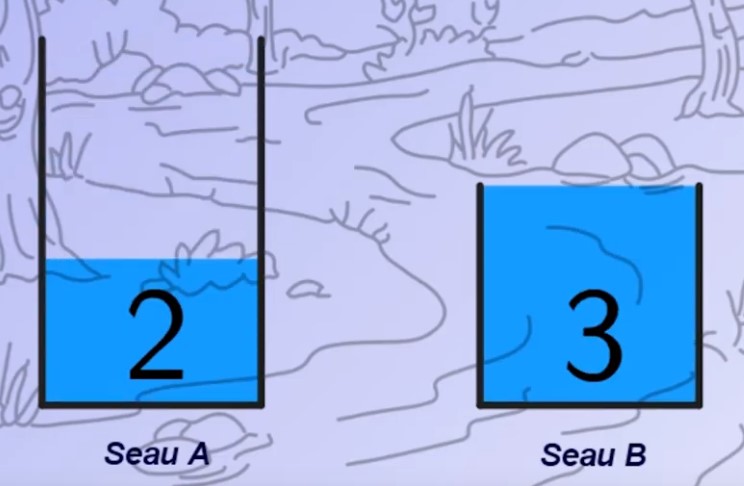
Deux seaux contiennent chacun la même quantité d’eau.
Un seau est à 210° F, tandis que l’autre est à 10° F.
D’une même hauteur et au même moment, vous laissez tomber deux boules de pétanque de dimensions et de poids identiques, une dans chaque seau.
Quelle boule touchera le fond de son seau en premier ?
. 267°/ L’ancre dans la flotte :
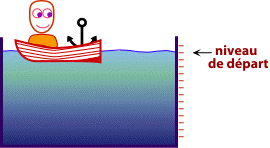
Vous êtes dans une petite embarcation dans une piscine.
(Que faites-vous là ? Vous êtes un marin d’eau douce, voyons… !)
Avec vous dans le bateau, il y a une ancre de 10 kg. Le niveau d’eau de la piscine est indiqué sur une échelle graduée.
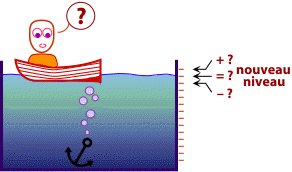
Vous décidez de balancer l’ancre dans la flotte. Le bateau allégé flottera un peu plus haut sur l’eau…
Mais qu’en est-il du niveau d’eau de la piscine ?
Montera-t-il, baissera-t-il ou restera-t-il égal ?
. 268°/ Les randonneurs rapides :
 Un beau samedi, à 6 h précises, vous entamez une randonnée pédestre. Votre but : atteindre le sommet du mont Washington, la montagne la plus élevée du nord-est des États-Unis.
Un beau samedi, à 6 h précises, vous entamez une randonnée pédestre. Votre but : atteindre le sommet du mont Washington, la montagne la plus élevée du nord-est des États-Unis.
 Deux heures plus tard, trois randonneurs en superbe forme physique vous dépassent. Leur but : établir un record pour l’aller-retour le plus rapide du mont Washington.
Deux heures plus tard, trois randonneurs en superbe forme physique vous dépassent. Leur but : établir un record pour l’aller-retour le plus rapide du mont Washington.
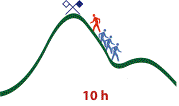 À 10 h, les trois randonneurs vous croisent sur leur chemin de retour. Ils se vantent qu’ils ne se sont pas arrêtés une seule seconde, même pas au sommet, où ils ont laissé leurs drapeaux.
À 10 h, les trois randonneurs vous croisent sur leur chemin de retour. Ils se vantent qu’ils ne se sont pas arrêtés une seule seconde, même pas au sommet, où ils ont laissé leurs drapeaux.
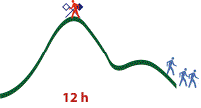 Finalement, vous atteignez le sommet à 12 h.
Finalement, vous atteignez le sommet à 12 h.
On suppose que votre vitesse d’ascension a été parfaitement uniforme.
On suppose aussi que les randonneurs ont maintenu une vitesse de marche parfaitement uniforme, en montant comme en descendant.
. 269°/ Le camion et l’oiseau :
 Un camion doit faire le trajet entre Montréal et Ottawa ; son poids total est d’exactement deux tonnes.
Un camion doit faire le trajet entre Montréal et Ottawa ; son poids total est d’exactement deux tonnes.
Ayant parcouru environ la moitié de la distance, le camion s’engage sur un pont dont la capacité maximale est de deux tonnes un gramme de plus, et le pont s’écroulerait.
Pendant que le camion roule sur le pont, un oiseau de 500 gr se pose dessus. Horreur !
Mais, non ! Pas de désastre, le pont tient le coup.
Pourquoi le pont ne s’est-il pas écroulé ?
. 270°/ Les trois témoignages :
Le détective soumet trois suspects à l’interrogatoire… Georges clame son innocence ainsi que celle de Jeanne. Jeanne affirme que Simone est coupable mais que Georges est innocent. Simone prétend qu’elle est innocente et que Jeanne est coupable.



En sachant que la personne coupable a menti et que les deux personnes innocentes ont dit la vérité…
…qui est coupable ?
. 271°/ L’âge des amis :
Thomas est plus jeune que Rose, mais plus vieux que Guillaume et Robert, dans cet ordre.
Rose est plus jeune que Suzanne, mais plus âgée que Robert.
Robert est plus jeune que Jean.
Suzanne est plus vieille que Rose, mais plus jeune que Jean.
Jean est plus vieux que Thomas.
Laquelle de ces personnes est la plus âgée ?
. 272°/ L’île des contraires :
Vous êtes sur une île sur laquelle il y a deux villages ; un est habité par des gens qui mentent toujours, et l’autre par des gens qui disent toujours la vérité.
Vous êtes en promenade dans le marché public et vous vous arrêtez devant le kiosque d’un vendeur de pommes, qui vous en tend une en vous invitant de l’acheter.
Bien que vous ayez envie d’un fruit, vous hésitez à accepter son offre, car vous avez lu les guides touristiques et vous savez que les habitants de l’île sont des vilains farceurs.
En effet, ils aiment bien embêter les touristes en introduisant un soporifique dans les fruits, ce qui écourte leur temps utile de vacances puisqu’ils tombent endormis pour deux jours ! Très drôle…
Malheureusement, vous ne savez pas si le vendeur provient du village de ceux qui disent la vérité ou de celui des menteurs.
Le vendeur vous propose de décider de l’achat ou non de la pomme après lui avoir posé une seule question.
Quelle est votre question ?
. 273°/ Une cinquième suite :
Quelles sont les deux prochaines lettres dans la suite suivante ?
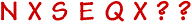
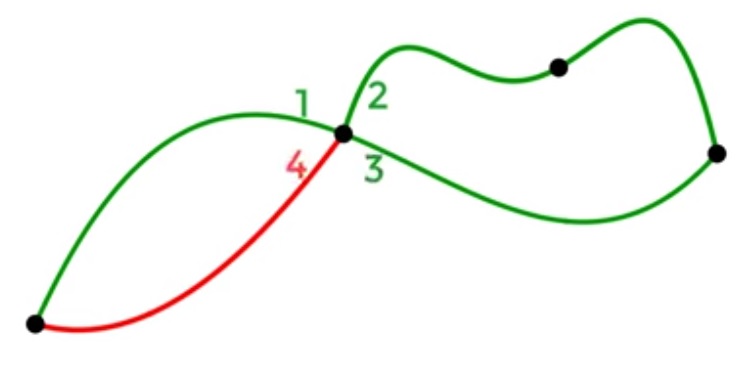
. 274°/ Les douze anneaux :


On vous a offert quatre chaînettes de trois anneaux chacune ; voir l’illustration à gauche. Vous désirez vous en servir pour confectionner un bracelet de douze anneaux, comme celui illustré à droite.
Puisque couper un anneau et le ressouder est un travail long et méticuleux, vous désirez fabriquer votre bracelet en coupant le minimum d’anneaux.
Quel est le nombre minimum d’anneaux que vous devez couper pour obtenir le bracelet ?
. 275°/ Les deux politiciens :
Georges et Jean l’un libéral, l’autre conservateur se font interviewer, et l’on sait qu’au moins l’un des deux ment. On leur demande leur allégeance politique ; voici leurs réponses :
Qui ment et qui dit la vérité ?
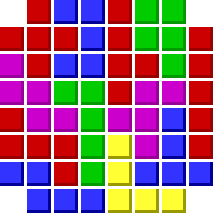
. 276°/ Les neuf cartes :

Dans un carré magique, la somme de chaque rangée, de chaque colonne et de chaque diagonale est toujours la même.
Neuf cartes sont placées comme dans le dessin. La somme de chaque rangée, de chaque colonne et d’une diagonale est égale à six. Ces neuf cartes ne constituent pas tout à fait un carré magique, puisqu’une diagonale n’est pas égale à six.
Changez la position de trois cartes afin que le carré soit complètement magique.
. 277°/ Le fou et l’asile :
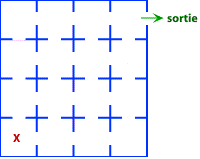
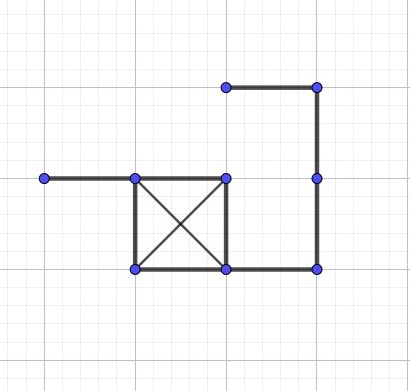
Un fou meurtrier interné dans un asile cherche à s’en échapper. L’asile est constitué de 16 chambres qui communiquent entre elles et il n’y a qu’une seule sortie de l’asile (voir le diagramme). Le fou se trouve dans la chambre marquée d’un ‘x.’ Toutes les chambres sont occupées par un seul patient.
Étant un fou meurtrier, il est obsessif et désire tuer chacun des 15 autres patients avant de s’évader.
Étant un meurtrier, il tuera chaque patient qu’il rencontrera dans les autres chambres, sans aucune pitié.
Étant un fou, il ne peut supporter la vue d’un cadavre, à tel point qu’il se suicidera si jamais il entre dans une chambre dans laquelle se trouve une de ses victimes.
Ainsi, il ne peut pas visiter une chambre contenant un cadavre.
Le fou ne peut pas percer les murs : il doit emprunter les portes existantes. La seule issue est la porte principale, marquée ‘sortie’ sur le diagramme.
Y a-t-il un parcours lui permettant de s’évader après avoir zigouillé les 15 patients ?
Si oui, lequel ? Sinon, pourquoi ?
. 278°/ La chambre à miroirs :
Vous êtes dans une chambre dont les quatre murs, le plancher et le plafond sont complètement recouverts de miroirs.
À part vous-même, il n’y a rien d’autre dans la chambre.
Combien de réflexions de vous-même voyez-vous ?
. 279°/ Le sultan et les disques :
Il était une fois un méchant sultan qui n’avait qu’un seul plaisir dans la vie : faire souffrir ses sujets. Un jour, il fit venir deux d’entre eux et leur dit, « J’ai décidé de m’amuser avec l’un d’entre vous, et vous allez déterminer lequel…
Il y a sur la table trois disques: un rouge et deux verts.
Je vais vous en fixer chacun un dans le dos sans que vous en voyiez la couleur, puis mes gardes vous enfermeront dans une pièce vide dans laquelle il n’y a aucun meuble, aucun objet, aucun miroir…
Le premier qui sortira de la pièce en me disant la couleur de disque qu’il a dans le dos pourra déguerpir. L’autre devra se soumettre à mes plaisirs sadiques ! » (Non, mais il n’est pas aimable du tout, le mec !)
Rendus dans la pièce, chacun inspecte le dos de l’autre, mais aucun ne coure vers la porte…
Mais au bout de quelque temps de réflexion, un des sujets ressort de la pièce en criant, « J’ai un disque vert dans le dos libérez moi ! »
Comment a-t-il fait pour le savoir ?
. 280°/ Les six carrés :
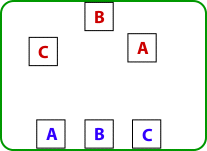
Six carrés sont disposés à l’intérieur d’un cadre comme dans le dessin.
Pouvez-vous tracer trois lignes pour connecter le carré A rouge au carré A bleu, le carré B rouge au carré B bleu et le carré C rouge au carré C bleu ?
Attention ! Il y a des contraintes :
¤ les lignes ne doivent pas se toucher ni se croiser
¤ les lignes ne peuvent pas toucher au cadre vert ni en sortir.
. 281°/ Les trois services :
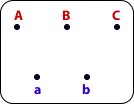
Dans un nouveau quartier où il n’y a pour le moment que deux maisons (a et b) on doit procéder au raccordement des services d’électricité, de gaz et d’eau (A, B et C). Afin de faire beau et propre, les conduits des trois services seront enfouis sous terre.
Il y a cependant deux contraintes importantes, imposées par une de ces lois de zonage bizarres.
Contraintes :
- chacun des trois services (A, B et C) doit être connecté à chacune des deux maisons (a, b).
- les lignes ne doivent pas se toucher ni se croiser, mais elles peuvent être longues et tortueuses.
Quels tracés doit-on emprunter ?
. 282°/ Le poisson à l’envers :
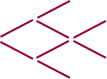
Voici un poisson qui nage vers la gauche. Il est confectionné à partir de huit baguettes (cure-dents, allumettes, etc.). On cherche à faire en sorte que le poisson nage vers la droite, en déplaçant les baguettes une à une.
Bien sûr, on peut le faire en déplaçant les huit baguettes.
Pouvez-vous retourner le poisson en ne déplaçant que 3 baguettes ?
. 283°/ Les trente lingots :
Un orfèvre fait venir un artiste peintre pour qu’il fasse le portrait de son épouse.
L’artiste lui dit qu’il lui faudra 30 jours pour réaliser l’œuvre, et qu’il désire être payé un centimètre d’or par jour, au jour le jour. 
Cela tombe bien, car l’orfèvre fabrique justement des lingots d’or de 30 cm. Mais il réalise que couper 29 fois un lingot, c’est bien fatigant et qu’étant un brin paresseux, il préfère faire le minimum de coupes…

[On supposera que les coupes sont tellement précises qu’il est possible de tailler des morceaux de lingot sans perte.]
Alors l’orfèvre consulte un ami qui lui dit qu’il devrait tailler un de ses lingots de 30 cm un certain nombre de fois pour obtenir X morceaux, et qu’avec ces X morceaux, il pourrait payer le peintre à chaque jour, pourvu qu’il interdise au peintre de dépenser son or avant la fin du contrat.
Combien de coupes au minimum sont nécessaires ?
Quelle est la longueur de chacun des morceaux résultants ?
. 284°/ Les points sur la sphère
Quel est le plus grand nombre de points équidistants qui peuvent être placés sur la surface d’une sphère (des points qui sont tous à la même distance l’un de l’autre) ?
Exemple d’exercice : La NASA veut placer des bases sur la lune. Combien peut-on en mettre au maximum pour qu’elles soient toutes à la même distance les unes des autres ?
. 285°/ Devinette 3 !
Qu’est-ce qui possède un chapeau et n’a point de tête, a un pied et ne possède point de soulier ?
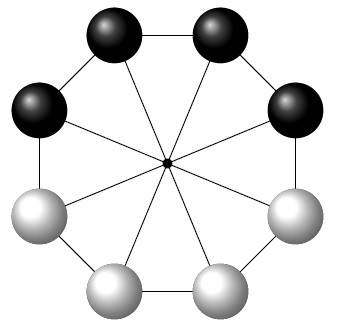
. 286°/ Le roi et les prisonniers :
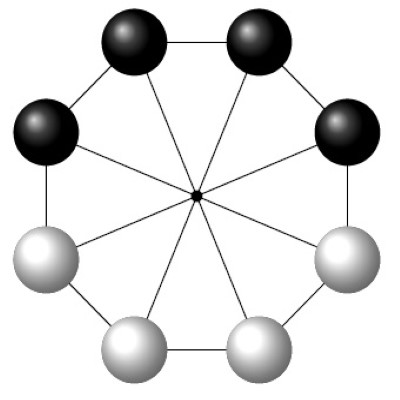
Un Roi décide de faire un jeu avec trois prisonniers, il les met en ligne, les uns derrière les autres, de sorte que le premier voit le dos des deux autres, le deuxième voit uniquement le dos du troisième, et le troisième ne voit rien. Ensuite, il leur dit, je vais vous mettre à chacun, une étiquette soit blanche soit noire dans le dos, j’ai 3 étiquettes noires et 2 étiquettes blanches. Vous devez essayer de deviner la couleur de l’étiquette que vous avez dans le dos, si vous trouvez, vous êtes libre, si vous vous trompez, c’est la mort, si vous ne savez pas, vous restez prisonnier.
Le premier dit : « Je ne peux pas savoir »
Le deuxième dit : « Je ne peux pas savoir »
Que va dire le troisième ?
. 287°/ La ville de Saint-Ludovic :
Dans la ville de Saint-Ludovic on remarque les faits suivants : (1) Il n’existe pas deux habitants ayant exactement le même nombre de cheveux. (2) Aucun habitant n’a exactement 518 cheveux. (3) il y plus d’habitants qu’il n’y a de cheveux sur la tête d’un quelconque d’entre eux.
Combien la ville de Saint-Ludovic a-t-elle d’habitants au plus ?
. 288°/ Pas jumeaux ?
Nous sommes nés le même jour, la même année, de la même mère à la même heure, pourtant nous ne sommes pas jumeaux. Pourquoi ?
. 289°/ Pour calculer mon âge, toute la famille participe !
Si j’écris mon âge trois fois à la suite, je retrouve le produit de mon âge par celui de ma femme et par ceux de nos quatre enfants. Si j’écris mon âge quatre fois à la suite, je retrouve le produit de mon âge par ceux qu’auraient, s’ils étaient encore vivants, mon père, mon grand-père et mon arrière-grand-père. D’autre part, mon âge est le quart de la différence de l’âge qu’aurait mon arrière-grand-père et mon plus jeune enfant. Quel est mon âge ?
. 290°/ L’épicerie :
Dans une épicerie, si une banane coûte 30 cts, une pomme 25 cts et une nectarine 45 cts. Combien coûterait selon cette logique une pêche ?
. 291°/ Dr Knock : Les deux épidémies :
La scène se déroule en 1923 : le docteur Parpalaid lègue sa clientèle à Knock, qui s’informe sur les gens de St-Maurice…
Knock – … Ce n’est pas en soignant les morts subites que vous avez pu faire fortune ?
Le docteur Parpalaid – Evidemment… Il nous reste d’abord la grippe. Pas la grippe banale qui ne les inquiète en aucune façon et qu’ils accueillent même avec faveur parce qu’ils prétendent qu’elle fait sortir les humeurs viciées. Non, je pense aux grandes épidémies mondiales.
Knock – Mais, ça, dites donc, c’est comme le vin de la comète, s’il faut que j’attende la prochaine épidémie mondiale…
Parpalaid – Moi qui vous parle, j’en ai vu deux.
Knock – Oui, mais c’était en quelles années ?
Parpalaid – Attendez que je me souvienne. Ces deux dates ne s’écrivaient qu’avec des 1, des 8 et des 9 ; mais ce n’était pas des multiples de 9 ; le nombre d’années qui les séparait non plus d’ailleurs (ce dernier se terminait cependant par un 9). Cela devait donc être en…
Quelles sont les dates de ces deux dernières épidémies mondiales de grippe ?
. 292°/ Les Suisses, les Souabes et les Saxons :
Un capitaine a trois compagnies : l’une de suisses, l’autre de souabes, l’autre de saxons. Il veut donner un assaut avec l’une de ses trois compagnies et il promet une récompense de 901 écus sur le critère suivant : que chaque soldat de la compagnie qui montera à l’assaut recevra un écu, et que le reste sera distribué équitablement aux deux autres compagnies. Or il se trouve que si les Suisses donnent l’assaut, chaque soldat des autres compagnies reçoit un demi écu, que si les Souabes vont à l’assaut, chaque soldat des autres compagnies reçoit un tiers écu, que si les Saxons donnent l’assaut chaque soldat des autres compagnies reçoit un quart écu. Combien y a t-il de Suisses, de Souabes et de Saxons ?
. 293°/ Qui ment et qui dit la vérité ?
Dans cette énigme, on considère trois personnes A, B, C qui soit mentent constamment soit disent tout le temps la vérité. Ces trois personnes firent les déclarations qui suivent. Pour chaque personne, trouvez qui ment et qui dit la vérité ?
A : « Seuls deux d’entre nous disent toujours la vérité. »
B : « Non, il n’y en a qu’un. »
C : « C’est vrai. »
. 294°/ Le prisonnier :
Une personne est prisonnière en haut d’une tour où il y a deux portes. L’une d’elle donne sur l’escalier du salut, l’autre sur le vide, donc la mort. Il y a deux gardiens. L’un dit toujours la vérité. L’autre ment toujours. Quelle seule et unique question doit poser le prisonnier à un seul des 2 gardiens pour être certain de trouver la porte du salut ?
. 295°/ Le frère et la sœur :
Alors qu’on demandait un jour à un frère et une sœur lequel des deux était le plus vieux, le frère répondit « Je suis le plus vieux » et la sœur « Je suis la plus jeune ». Il s’avéra qu’au moins un des deux mentait. Qui est le plus vieux et qui ment ?
. 296°/ L’hôpital psychiatrique 2 :
Le journaliste continue ces questions et se trouvent face à 3 personnes A, B, C qui lui disent :
A : « Aucun de nous n’est un médecin »
B : « Je suis un docteur »
C : « Au moins deux d’entre nous sont des malades »
Alors, qui est médecin et qui est patient ?
. 297°/ Six petits flacons :
On possède six petits flacons d’une capacité respective de 16cc, 18cc, 22cc, 23cc, 24cc et 34cc. On remplit quelques-uns de ces flacons d’eau, d’autres d’alcool et un dernier reste vide.
On s’aperçoit alors que ce tout est constitué de deux fois plus d’alcool que d’eau.
Quel est le flacon vide ?
Quels flacons furent utilisés pour l’eau ? Pour l’alcool ?
. 298°/ De l’eau dans son vin :
Un verre de vin est à demi rempli de vin. Un deuxième verre, d’une capacité double au premier, est rempli au quart de vin. Pour remplir complètement ces verres, on décide d’ajouter de l’eau.
On les transvide alors dans un contenant quelconque. Quelle est la proportion de vin de ce nouveau mélange ?
. 299°/ Les équipes de hockey :
La fiche de pointage de trois différentes équipes de hockey est incomplète. Vous devez la compléter en sachant qu’aucun club n’a joué deux fois contre le même adversaire. Je veux aussi le score des parties qui furent disputées.
|
A |
B |
C |
| Nombre de parties jouées |
? |
2 |
? |
| Nombre de parties gagnées |
? |
? |
? |
| Nombre de parties perdues |
1 |
1 |
? |
| Nombre de parties nulles |
? |
1 |
? |
| Nombre de points pour |
3 |
0 |
? |
| Nombre de points contre |
2 |
? |
1 |











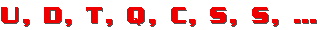


 C’est un pays imaginaire où les habitants ne peuvent communiquer que par la Poste. Malheureusement, les postiers de ce pays sont tous, sans exception, des voleurs systématiques.
C’est un pays imaginaire où les habitants ne peuvent communiquer que par la Poste. Malheureusement, les postiers de ce pays sont tous, sans exception, des voleurs systématiques. Deux habitants de ce pays, Pierre et Paul, désirent s’échanger du courrier. Ils ne veulent pas que des yeux indiscrets puissent lire leur courrier, alors pas question de tout simplement écrire le message sur la boîte ! Vu qu’il n’y a qu’une seule clé pour chaque cadenas et qu’ils n’ont pas le loisir de se rencontrer pour s’échanger leurs clés respectives…
Deux habitants de ce pays, Pierre et Paul, désirent s’échanger du courrier. Ils ne veulent pas que des yeux indiscrets puissent lire leur courrier, alors pas question de tout simplement écrire le message sur la boîte ! Vu qu’il n’y a qu’une seule clé pour chaque cadenas et qu’ils n’ont pas le loisir de se rencontrer pour s’échanger leurs clés respectives…

































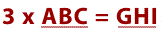





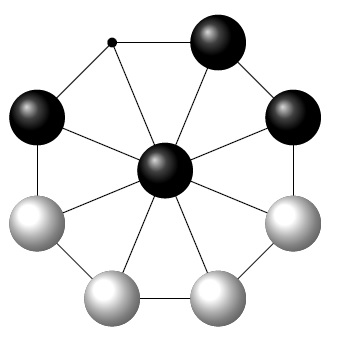
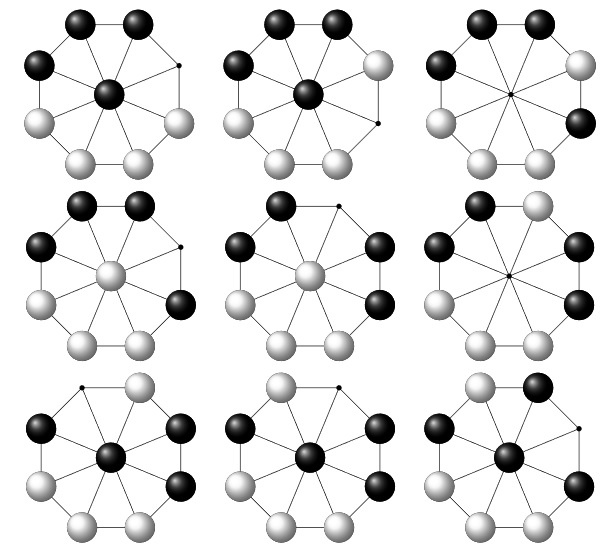
 Quelle est la prochaine ligne de cette suite ?
Quelle est la prochaine ligne de cette suite ?


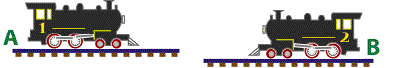



 Un panier d’œufs coûte 1,10 $.
Un panier d’œufs coûte 1,10 $.
 Combien coûtent les œufs?
Combien coûtent les œufs?


 Un beau samedi, à 6 h précises, vous entamez une randonnée pédestre. Votre but : atteindre le sommet du mont Washington, la montagne la plus élevée du nord-est des États-Unis.
Un beau samedi, à 6 h précises, vous entamez une randonnée pédestre. Votre but : atteindre le sommet du mont Washington, la montagne la plus élevée du nord-est des États-Unis. Deux heures plus tard, trois randonneurs en superbe forme physique vous dépassent. Leur but : établir un record pour l’aller-retour le plus rapide du mont Washington.
Deux heures plus tard, trois randonneurs en superbe forme physique vous dépassent. Leur but : établir un record pour l’aller-retour le plus rapide du mont Washington. À 10 h, les trois randonneurs vous croisent sur leur chemin de retour. Ils se vantent qu’ils ne se sont pas arrêtés une seule seconde, même pas au sommet, où ils ont laissé leurs drapeaux.
À 10 h, les trois randonneurs vous croisent sur leur chemin de retour. Ils se vantent qu’ils ne se sont pas arrêtés une seule seconde, même pas au sommet, où ils ont laissé leurs drapeaux. Finalement, vous atteignez le sommet à 12 h.
Finalement, vous atteignez le sommet à 12 h. Un camion doit faire le trajet entre Montréal et Ottawa ; son poids total est d’exactement deux tonnes.
Un camion doit faire le trajet entre Montréal et Ottawa ; son poids total est d’exactement deux tonnes.



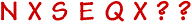







































 .
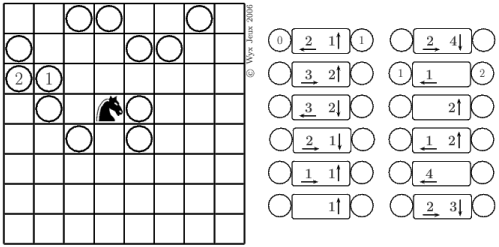
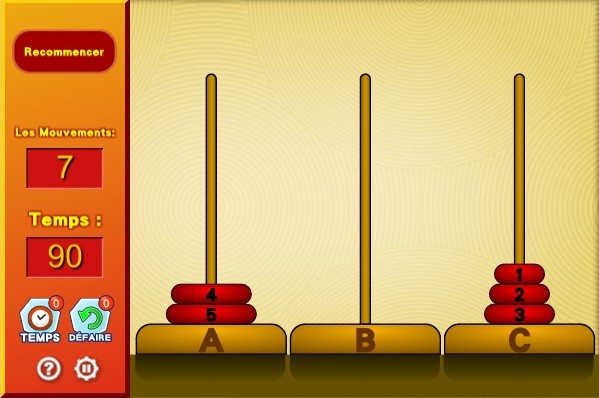
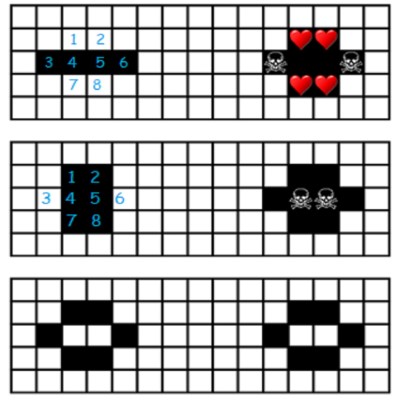
. qui devra aller d’un rond à l’autre jusqu’au dernier.
qui devra aller d’un rond à l’autre jusqu’au dernier. et le deuxième
et le deuxième  arrêt sont indiqués.
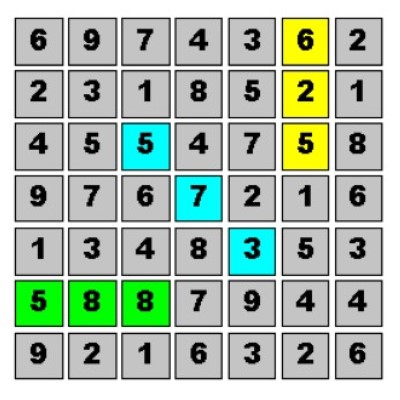
arrêt sont indiqués. correspond à un déplacement de 3 cases vers la gauche et deux cases vers le bas, c’est-à-dire tout simplement à une translation de vecteur u(-3, -2). Ces 12 déplacements sont deux à deux différents.
correspond à un déplacement de 3 cases vers la gauche et deux cases vers le bas, c’est-à-dire tout simplement à une translation de vecteur u(-3, -2). Ces 12 déplacements sont deux à deux différents.