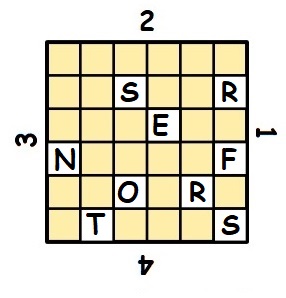
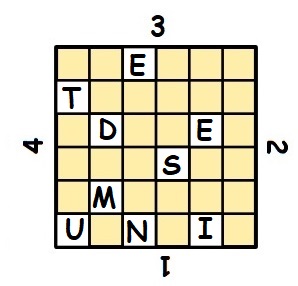
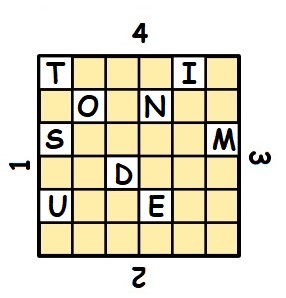
Un triplet pythagoricien, ou triplet de Pythagore, est un ensemble de 3 nombres entiers naturels non nuls vérifiant le théorème de Pythagore : a² + b² = c². Le triplet pythagoricien le plus connu est (3, 4, 5).
Il en existe une infinité et l’intérêt est de trouver une méthodes pour les trouver tous.
I°/ La suite de Fibonacci :
II°/ Le triplet (3n,4n,5n) :
III°/ Généralisation :
IV°/ Une autre formule :
V°/ Des triplets très particuliers :
I°/ La suite de Fibonacci :
Il existe une infinité de triplets Pythagoricien. On peut en retrouver certains grâce à la suite de Fibonacci.
Pour rappel, la suite de Fibonacci consiste à partir du nombre 0 puis 1, et à additionner les nombres deux à deux à l’infini :
1 1 2 3 5 8 13 21 … ( en effet : 1 0 + 1 = 1 1 + 1 = 2 1 + 2 = 3 2 + 5 = 5 …)
Pour trouver quelques nombres Pythagoriciens, il suffit de prendre 4 nombres qui se suivent dans la suite de Fibonacci et d’effectuer les calculs suivants :
Soient w, x, y et z, 4 nombres la suite de Fibonacci et a, b et c les triplets Pythagoricien : a = wz ; b = 2xy et c = wy + xz.
| La suite Fibonacci : | ||||||||||||||||||||||
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 | 10946 | 17711 |
| w | x | y | z | |||||||||||||||||||
Utilisons les nombres la suite de Fibonacci :
| Les triplets Pythagoriciens : | |||||||
| w=1 ; x=1 ; y=2 ; z=3 | w=1 ; x=2 ; y=3 ; z=5 | w=2 ; x=3 ; y=5 ; z=8 | w=3 ; x=5 ; y=8 ; z=13 | w=5 ; x=8 ; y=13 ; z=21 | w=8 ; x=13 ; y=21 ; z=34 | w=13 ; x=21 ; y=34 ; z=55 | |
| a = wz | 1×3 = 3 | 1×5 = 5 | 2×8 = 16 | 3×13 = 39 | 5×21 = 105 | 8×34 = 272 | 13×55 = 715 |
| b = 2xy | 2x1x2 = 4 | 2x2x3 = 12 | 2x3x5 = 30 | 2x5x8 = 80 | 2x8x13 = 208 | 2x13x21 = 546 | 2x21x34 = 1428 |
| c = wy + xz | 1×2 + 1×3 = 5 | 1×3 + 2×5 = 13 | 2×5 + 3×8 = 34 | 3×8 + 5×13 = 89 | 5×13 + 8×21 = 233 | 8×21 + 13×34 = 610 | 13×34 + 21×55 = 1597 |
| Théorème de Pythagore : | |||||||
| a² + b² = | 3² + 4² = 25 | 5² + 12² = 169 | 16² + 30² = 1156 | 39² + 80² = 7921 | 105² + 208² = 54289 | 272² + 546² = 372100 | 715² + 1428² = 2550409 |
| c² = | 5² = 25 | 13² = 169 | 34² = 1156 | 89² = 7921 | 233² = 54289 | 610² = 372100 | 1597² = 2550409 |
Démonstration : 4 nombres la suite de Fibonacci w, x, y = w + x et z = x + y = x + w + x = 2x + w
triplets Pythagoricien a, b et c : c² = a² + b²
c² = (wy + xz)² = w²y² + 2wxyz + x²z² = w²(w + x)² + 2wx(w + x)(2x + w) + x²(2x + w)² = w²(w² + 2wx + x²) + 2wx(2wx + w² + 2x² + wx) + x²(4x² + 4wx + w²)
= w4 + 2w3x + w²x² + 4w²x² + 2w3x + 4wx3 + 2w²x² + 4x4 + 4wx3 + w²x² = w4 + 4x4 + 4w3x + 8wx3 + 8 w²x²
a² + b²= w²z² + 4x²y² = w²(2x + w)² + 4x²( w + x)² = w²(4x² + 4wx + w²) + 4x²(w² + 2wx + x²) = 4w²x² + 4w3x + w4 + 4w²x² + 8wx3 + 4x4 = w4 + 4x4 + 4w3x + 8wx3 + 8w²x²
II°/ Le triplet (3n,4n,5n) :
Le triplet le plus connu est (3, 4, 5) : en effet 3² + 4² = 9 + 16 = 25 = 5².
De fait, les triplets de la forme (3n, 4n ,5n) sont aussi pythagoricien : (3n)² + (4n)² = 9n² + 16n² = 25n² = (5n)².
III°/ Généralisation :
On peut en trouver d’autre : 5² + 12² = 25 + 144 = 169 = 13² et leur variantes : (5n)² + (12n)² = 25n² + 144n² = 169n² = (13n)².
Tout triplet pythagoricien (a,b,c) peut s’obtenir de la façon suivante : Choisir trois entiers naturels quelconques u,v et n, avec u strictement plus grand que v, et poser :
| u | v | n | a | b | c | a² | b² | a²+ b² | c² |
| 2 | 1 | 1 | 3 | 4 | 5 | 9 | 16 | 25 | 25 |
| 2 | 1 | 2 | 6 | 8 | 10 | 36 | 64 | 100 | 100 |
| 2 | 1 | 3 | 9 | 12 | 15 | 81 | 144 | 225 | 225 |
| 3 | 2 | 2 | 10 | 24 | 26 | 100 | 576 | 676 | 676 |
| 2 | 1 | 5 | 15 | 20 | 25 | 225 | 400 | 625 | 625 |
| 3 | 2 | 1 | 5 | 12 | 13 | 25 | 144 | 169 | 169 |
| 10 | 5 | 2 | 150 | 200 | 250 | 22500 | 40000 | 62500 | 62500 |
IV°/ Une autre formule :
Il existe une formule « magique » et très élégante qui permet trouver une infinité de triplet.
| x | 2x+1 | x+x/(2x+1) | Numérateur 2x²+2x | Dénominateur 2x+1 | Hypoténuse 2x²+2x+1 | Num²+ Dén² | Hypo² |
| 1 | 3 | 1 + 1/3 = 4/3 | 4 | 3 | 5 | 25 | 25 |
| 2 | 5 | 2 + 2/5 = 12/5 | 12 | 5 | 13 | 169 | 169 |
| 3 | 7 | 3 + 3/7 = 24/7 | 24 | 7 | 25 | 625 | 625 |
| 4 | 9 | 4 + 4/9 = 40/9 | 40 | 9 | 41 | 1681 | 1681 |
| 5 | 11 | 5 + 5/11 = 60/11 | 60 | 11 | 61 | 3721 | 3721 |
| 6 | 13 | 6 + 6/13 = 84/13 | 84 | 13 | 85 | 7225 | 7225 |
| 7 | 15 | 7 + 7/15 = 112/15 | 112 | 15 | 113 | 12769 | 12769 |
| 8 | 17 | 8 + 8/17 = 144/17 | 144 | 17 | 145 | 21025 | 21025 |
Cherchez des triplets :
V°/ Des triplets très particuliers :
1°/ Un triplet compliqué :
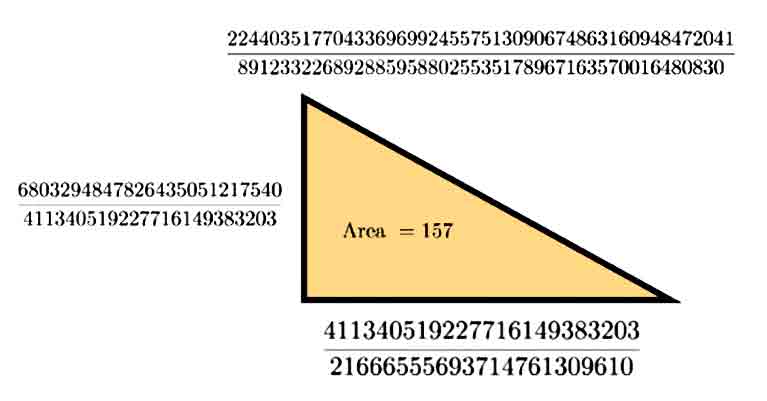 |
Voici un triangle rectangle avec des côtés rationnels (le côté le plus long a un dénominateur de 45 chiffres !) et une aire de 157 a été découvert par Don Zagier en 1993. |
2°/ Une hypoténuse paradoxale de longueur nulle :
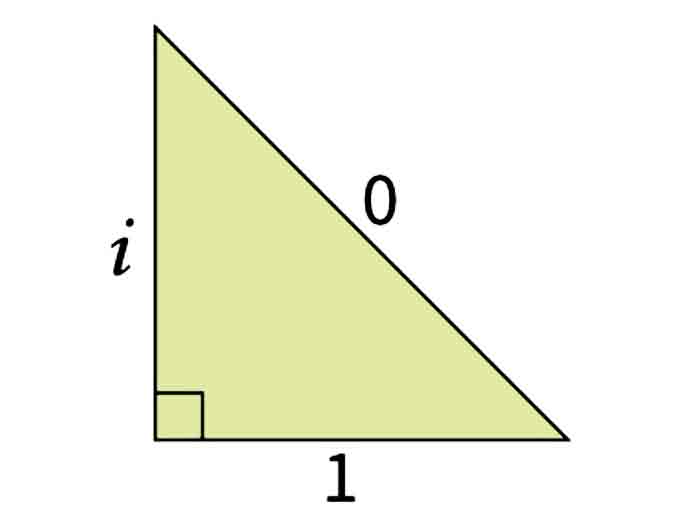 |
Un étrange triangle rectangle impliquant le nombre imaginaire unitaire i.
Le carré du nombre complexe i est égal à -1, donc : i² + 1 ² = -1 + 1 = 0 !!!!!!! C’est bien sûr n’importe quoi, mais c’est amusant. |
3°/ Un triangle rectangle magique :
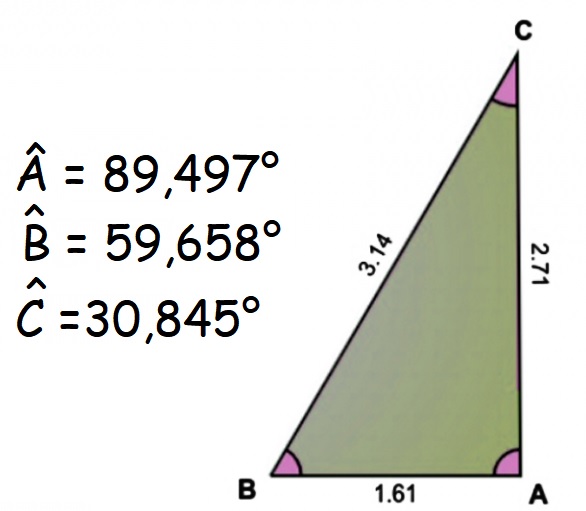 |
Un triangle avec des côtés π (3,14), e (2,71) et le nombre d’or (1,61) est presque un triangle rectangle ! |
4°/ Triangle de Kepler :
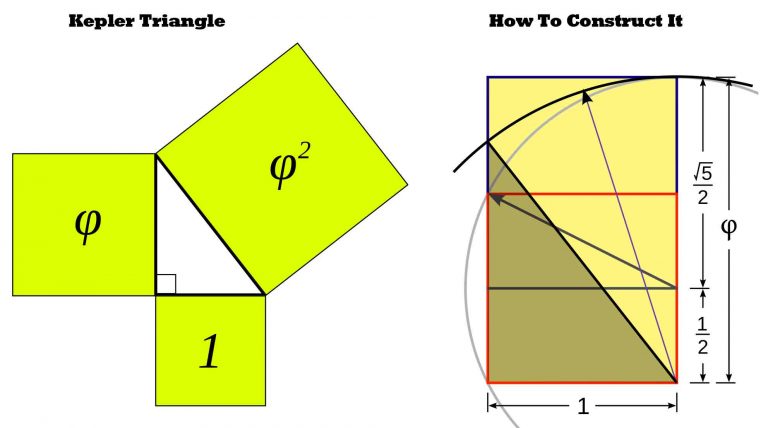 |
Un triangle de Kepler est un triangle rectangle formé de trois carrés dont les aires sont en progression géométrique selon le nombre d’or.
Ce triangle a pour côté 1,\sqrt{\varphi} et \varphi, donc on a bien : \sqrt{\varphi}^{2}+1^{2}=\varphi+1=\varphi^{2} |
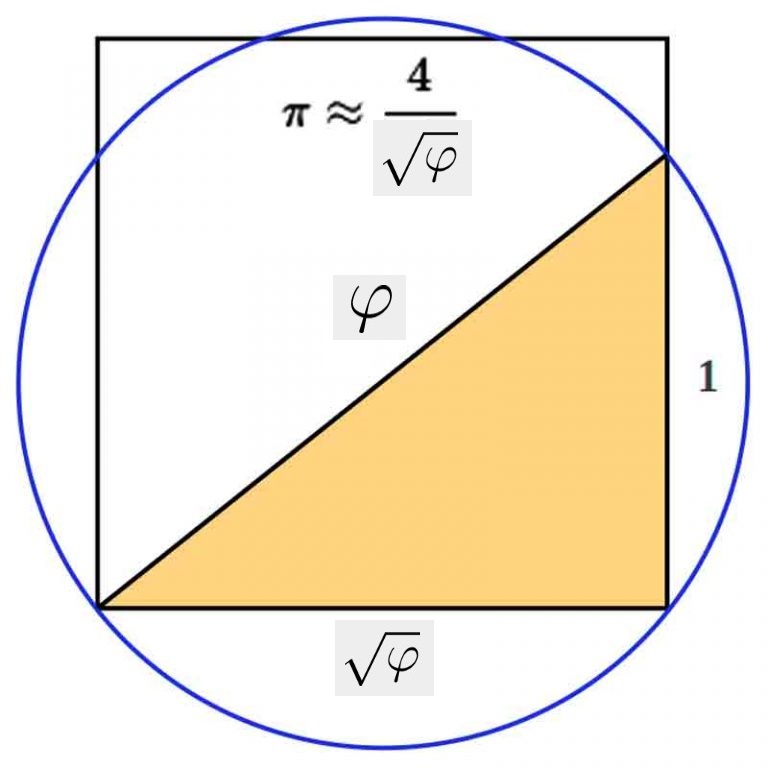 |
Traçons le cercle circonscrit au triangle de Kepler dont le diamètre est l’hypoténuse du triangle. Les périmètres du carré (4\sqrt{\varphi} ≈ 5,0884) et du cercle (2\pi R=2\pi\frac{\varphi}{2}=\pi\varphi ≈ 5,083) sont presque égaux avec une erreur inférieure à 0,1 %.De là, nous pouvons obtenir la coïncidence d’approximation : 4\sqrt{\varphi}=\pi\varphi\Rightarrow\pi=\frac{4\sqrt{\varphi}}{\varphi}=\frac{4}{\sqrt{\varphi}}
|
5°/ Triangle rectangle de Fibonacci :
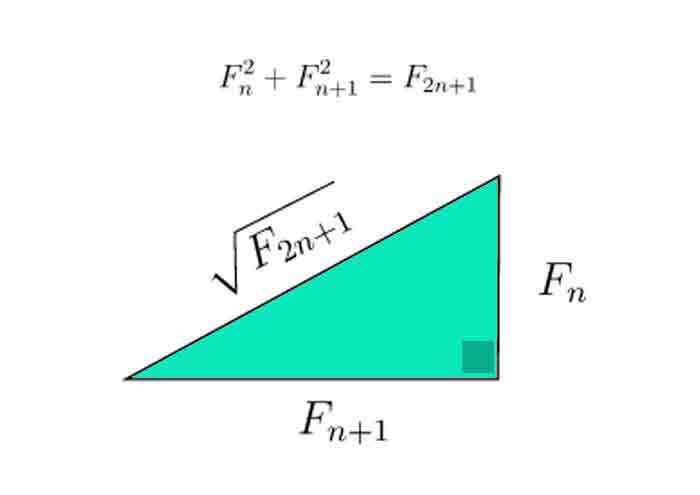 |
La somme des carrés de nombres de Fibonacci consécutifs est un autre nombre de Fibonacci. |