Le nom Système international d’unités, et l’abréviation SI, ont été établis par la 11e Conférence générale des poids et mesures (CGPM) en 1960.
La création des unités fut longue et laborieuse, car chaque pays, voire chaque région possédait ses propres unités de mesure. Par exemple, la longueur de référence au moyen âge était le pied, qui correspondait à la longueur du pied du seigneur des lieux. Chaque seigneur imposait son propre pied, qui variait d’une région à l’autre, et qui pouvait même changer à la mort de celui-ci.

Tableau de conversion. |
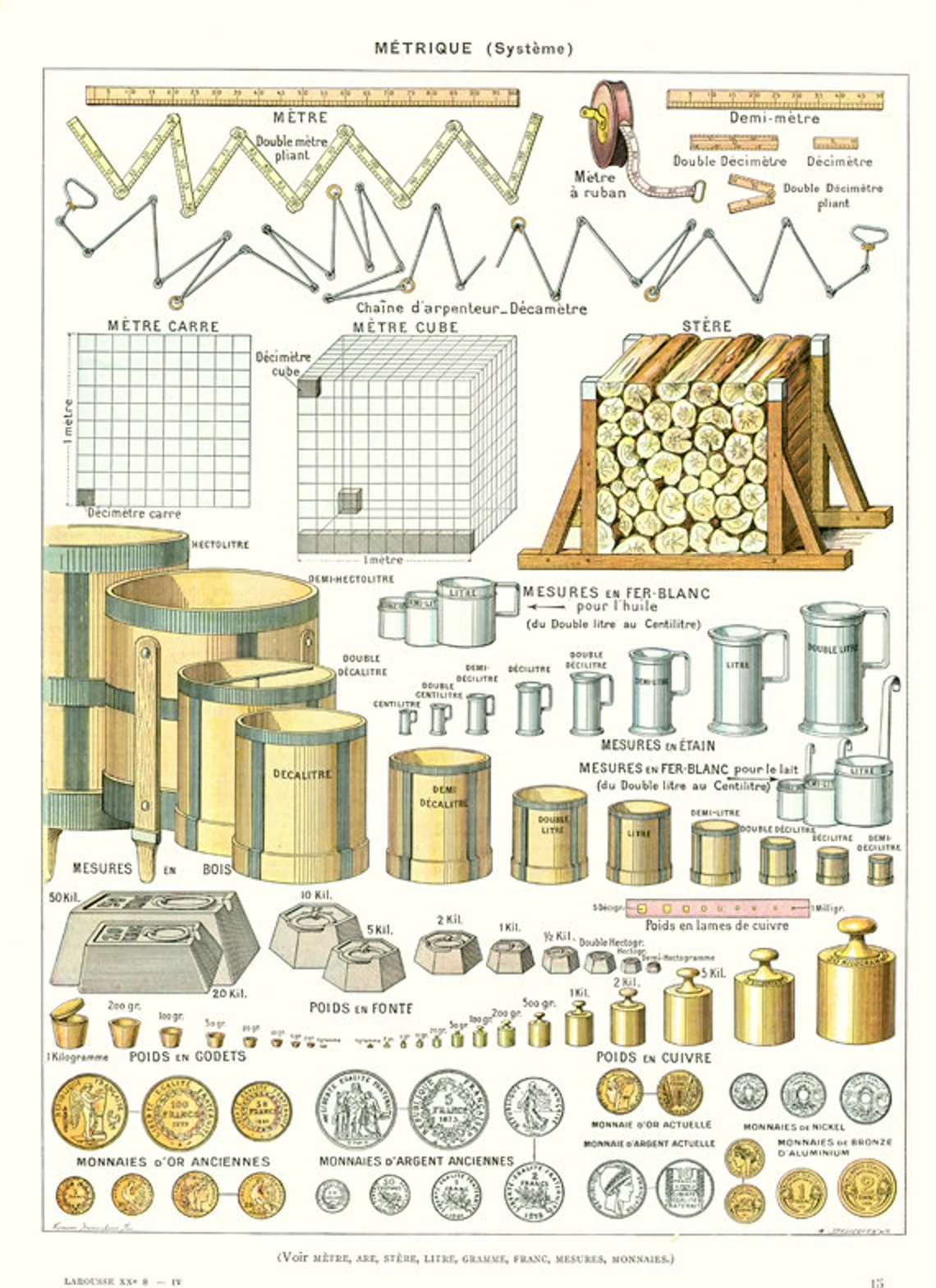
Très belle affiche datant du 20ième siècle. |
C’est durant la révolution Française que l’Académie royale des sciences de Paris adopte et impose le mètre comme mesure pour toute la France. Les anciennes unités de coudées, de pieds ou de pouces sont toutes abandonnées. Des mètres étalons apparaissent sur toutes les mairies pour que la France adopte cette nouvelle mesure.

I°/ Définitions des unités de base :
II°/ Les unités dérivées du SI :
III°/ L’histoire du mètre :
I°/ Définitions des unités de base :
Il existe 7 unités de base qui permettent de mesurer tout ce qui nous entoure : la longueur en mètre, la masse en kilogramme, le temps en seconde, le courant électrique en ampère, la température en kelvin , la quantité de matière en mole et l’intensité lumineuse en candela.
A partir de ces 7 unités on peut alors construire toutes les autres. Par exemple la vitesse est mesurée en km/h.
| Mesures | Temps t |
Distance D |
Masse m |
Intensité électrique I |
Température T |
Quantité de matière n |
Intensité lumineuse Iv |
| Unités | Seconde | Mètre | Kilogramme | Ampère | Kelvin | Mole | Candela |
| Symbole | s | m | kg | A | k | mol | Cd |
| Définition historique | 1re définition en 1889 : la durée du jour terrestre divisée en 24 h de 60 min de 60 s.
2ième définition en 1960 : durée de l’année 1900 divisée par 31 556 925,9757 |
1re définition en 1791 : un dix-millionième du quart de la circonférence de la terre | 1re définition en 1799 : poids d’un litre d’eau à 4°C.
2ième définition en 1889 : un étalon en alliage de 90% de platine et de 10% d’iridium |
1re définition en 1946 : correspondant au transport d’une charge électrique d’1 coulomb par seconde (C/s) à travers une surface. | 1re définition en 1954 : degré d’agitation des molécules basée sur une fraction de la température thermodynamique du point triple de l’eau (à la fois liquide, solide et gazeuse). 1 K = 1/273,16. | 1re définition en 1971 : nombre d’atomes dans 0,012 kilogramme de carbone 12 | 1re définition en 1954, remplaçant l’unité de la bougie établie à 60 bougies par centimètre carré. |
| Définition moderne | 9 192 631 770 x période de rayonnement de Césium 133 | Distance parcourue par la lumière pendant 1/299 792 458 seconde | Constante de Planck = 6,626 070 15 × 10−34 s−1 m2 kg ou Joule-seconde | Charge élémentaire = 1,602 176 634 × 10−19 Coulombs ou Ampère – seconde | Constante de Boltzmann = 1,380 649 × 10−23 s−2 m2 kg K−1 ou Joule/Kelvin | Nombre d’Avogadro = 6,022 140 76 × 1023 mol-1 | Intensité énergétique d’un rayonnement monochromatique de fréquence 540 × 1012 s−1 (hertz) = 683 s3 m−2 kg−1 cd sr, ou cd sr W−1, ou lm W−1 |
Les définitions historiques posent des problèmes de nos jours où les mesures se doivent d’être beaucoup plus précises, car elles reposent sur de la matière qui évolue dans le temps et perd donc en précision. Le mètre étalon ou le kilogramme repose depuis 1889 sur des objets en platine et iridium (90% et 10%) qui se dégradent au fil du temps du fait de la désintégration de ces atomes. On sait que certains poids étalons ont varié d’environ 50 µg en un siècle.
A présent il faut graver les puces électroniques au nanomètre (milliardième de mètre), peser précisément les molécules des médicaments, mesurer le temps correctement pour nos futurs voyages intersidéraux …. Il était nécessaire de revoir complétement notre système de mesure.
Il fut donc décidé, lors de la 26e Conférence générale des poids et mesures (CGPM) à Versailles, de baser notre nouveau SI sur des constantes universelles, qui sont des invariants de la nature (indépendant du temps et de l’espace) à caractère universel ce qui permettra d’assurer la stabilité à long terme des nouvelles définitions. Le nouveau SI entre en vigueur le 20 mai 2019 à l’occasion de la journée mondiale de la métrologie. La seconde permet de définir le mètre, la seconde et le mètre permettent de définir le kilogramme et ainsi de suite.
Mètre, kilo, seconde : Les sorciers prennent des mesures, une vidéo de l’émission « C’est pas sorcier ». Sabine et Jamy nous emmènent dans l’univers de la métrologie (la science des unités de mesure).
II°/ Les unités dérivées du SI :
1°/ Unité SI dérivée cohérente :
2°/ Unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
3°/ Exemples d’unités SI dérivées cohérentes dont le nom et le symbole comprennent des unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
4°/ Unités en dehors du SI dont l’usage est accepté avec le SI :
5°/ Unités en dehors du SI dont la valeur en unités SI est obtenue expérimentalement :
6°/ Autres unités en dehors du SI :
7°/ Unités en dehors du SI associées aux systèmes d’unités CGS :
8°/ Préfixes et multiples SI :
Les unités dérivées du SI sont formées des produits de puissances des unités de base, et quand le produit des puissances ne comprend pas de facteur numérique autre que 1, les unités dérivées sont appelées unités dérivées cohérentes.
La valeur numérique d’une grandeur dépend du choix de l’unité. Par exemple, la valeur numérique d’une vitesse peut être de 25 m/s ou de 90 km/h selon l’unité choisie.
1°/ Unité SI dérivée cohérente :
|
Grandeur dérivée |
Unité SI dérivée cohérente |
||
|
Nom |
Symbole |
Nom |
Symbole |
| superficie |
A |
mètre carré |
m2 |
| volume |
V |
mètre cube |
m3 |
| vitesse |
v |
mètre par seconde |
m s-1 |
| accélération |
a |
mètre par seconde carrée |
m s-2 |
| nombre d’ondes |
σ |
mètre à la puissance moins un |
m-1 |
| masse volumique |
ρ |
kilogramme par mètre cube |
kg m-3 |
| masse surfacique |
ρA |
kilogramme par mètre carré |
kg m-2 |
| volume massique |
v |
mètre cube par kilogramme |
m3kg-1 |
| densité de courant |
j |
ampère par mètre carré |
A m-2 |
| champ magnétique |
H |
ampère par mètre |
A m-1 |
| concentration de quantité de matière |
c |
mole par mètre cube |
mol m-3 |
| concentration massique |
ρ, γ |
kilogramme par mètre cube |
kg m-3 |
| luminance lumineuse |
Lv |
candela par mètre carré |
cd m-2 |
| indice de réfraction |
n |
(le nombre) un |
1 |
| perméabilité relative |
μr |
(le nombre) un |
1 |
2°/ Unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
|
Unité SI dérivée cohérente |
||||
|
Grandeur dérivée |
Nom |
Symbole |
Expression utilisant d’autres unités SI |
Expression en unités SI de base |
| angle plan | radian |
rad |
1 |
m m-1 |
| angle solide | stéradian |
sr |
1 |
m2 m-2 |
| fréquence | hertz |
Hz |
s-1 |
|
| force | newton |
N |
m kg s-2 |
|
| pression, contrainte | pascal |
Pa |
N/m2 |
m-1 kg s-2 |
| énergie, travail, quantité de chaleur | joule |
J |
N m |
m2 kg s-2 |
| puissance, flux énergétique | watt |
W |
J/s |
m2 kg s-3 |
| charge électrique, quantité d’électricité | coulomb |
C |
s A |
|
| différence de potentiel électrique force électromotrice | volt |
V |
W/A |
m2 kg s-3 A-1 |
| capacité électrique | farad |
F |
C/V |
m-2 kg-1 s4 A2 |
| résistance électrique | ohm |
Ω |
V/A |
m2 kg s-3 A-2 |
| conductance électrique | siemens |
S |
A/V |
m-2 kg-1 s3 A2 |
| flux d’induction magnétique | weber |
Wb |
V s |
m2 kg s-2 A-1 |
| induction magnétique | tesla |
T |
Wb/m2 |
kg s-2 A-1 |
| inductance | henry |
H |
Wb/A |
m2 kg s-2 A-2 |
| température Celsius | degré Celsius |
°C |
K |
|
| flux lumineux | lumen |
lm |
cd sr |
cd |
| luminance lumineuse | lux |
lx |
lm/m2 |
m-2 cd |
| activité d’un radionucléide | becquerel |
Bq |
s-1 |
|
| dose absorbée, énergie massique (communiquée), kerma | gray |
Gy |
J/kg |
m2 s-2 |
| équivalent de dose, équivalent de dose ambiant, équivalent de dose directionnel, équivalent de dose individuel | sievert |
Sv |
J/kg |
m2 s-2 |
| activité catalytique | katal |
kat |
s-1 mol |
|
3°/ Exemples d’unités SI dérivées cohérentes dont le nom et le symbole comprennent des unités SI dérivées cohérentes ayant des noms spéciaux et des symboles particuliers :
|
Unité SI dérivée cohérente |
|||
|
Grandeur dérivée |
Nom |
Symbole |
Expression en unités SI de base |
| viscosité dynamique | pascal seconde |
Pa s |
m-1 kg s-1 |
| moment d’une force | newton mètre |
N m |
m2 kg s-2 |
| tension superficielle | newton par mètre |
N/m |
kg s-2 |
| vitesse angulaire | radian par seconde |
rad/s |
m m-1 s-1 = s-1 |
| accélération angulaire | radian par seconde carrée |
rad/s2 |
m m-1 s-2 = s-2 |
| flux thermique surfacique, éclairement énergétique | watt par mètre carré |
W/m2 |
kg s-3 |
| capacité thermique, entropie | joule par kelvin |
J/K |
m2 kg s-2 K-1 |
| capacité thermique massique, entropie massique | joule par kilogramme kelvin |
J/(kg K) |
m2 s-2 K-1 |
| énergie massique | joule par kilogramme |
J/kg |
m2 s-2 |
| conductivité thermique | watt par mètre kelvin |
W/(m K) |
m kg s-3 K-1 |
| énergie volumique | joule par mètre cube |
J/m3 |
m -1 kg s-2 |
| champ électrique | volt par mètre |
V/m |
m kg s-3 A-1 |
| charge électrique volumique | coulomb par mètre cube |
C/m3 |
m-3 s A |
| charge électrique surfacique | coulomb par mètre carré |
C/m2 |
m-2 s A |
| induction électrique, déplacement électrique | coulomb par mètre carré |
C/m2 |
m-2 s A |
| permittivité | farad par mètre |
F/m |
m-3 kg-1 s4 A2 |
| perméabilité | henry par mètre |
H/m |
m kg s-2 A-2 |
| énergie molaire | joule par mole |
J/mol |
m2 kg s-2 mol-1 |
| entropie molaire, capacité thermique molaire | joule par mole kelvin |
J/(mol K) |
m2 kg s-2 K-1 mol-1 |
| exposition (rayons x et γ) | coulomb par kilogramme |
C/kg |
kg-1 s A |
| débit de dose absorbée | gray par seconde |
Gy/s |
m2 s-3 |
| intensité énergétique | watt par stéradian |
W/sr |
m4 m-2 kg s-3 = m2 kg s-3 |
| luminance énergétique | watt par mètre carré stéradian |
W/(m2 sr) |
m2 m-2 kg s-3 = kg s-3 |
| concentration de l’activité catalytique | katal par mètre cube |
kat/m3 |
m-3 s-1 mol |
4°/ Unités en dehors du SI dont l’usage est accepté avec le SI :
|
Grandeur |
Nom de l’unité |
Symbole de l’unité |
Valeur en unités SI |
| temps, durée | minute |
min |
1 min = 60 s |
| heure |
h |
1 h = 60 min = 3 600 s | |
| jour |
d |
1 d = 24 h = 86 400 s | |
| angle plan | degré |
° |
1° = (π/180) rad |
| minute |
‘ |
1′ = (1/60)° = (π/10 800) rad | |
| seconde |
« |
1″ = (1/60)’ = (π/648 000) rad | |
| superficie | hectare |
ha |
1 ha = 1hm2 = 104 m2 |
| volume | litre |
L, l |
1 L = 1 dm3 = 10-3 m3 |
| masse | tonne |
t |
1 t = 103 kg |
5°/ Unités en dehors du SI dont la valeur en unités SI est obtenue expérimentalement :
|
Grandeur |
Nom de l’unité |
Symbole de l’unité |
Valeur en unités SI |
| Unités en usage avec le SI | |||
| énergie | électronvolt |
eV |
1 eV = 1.602 176 53(14)×10-19 J |
| masse | dalton, |
Da |
1 Da = 1.660 538 86(28)×10-27 kg |
| unité de masse atomique unifiée |
u |
1 u = 1 Da | |
| longueur | unité astronomique |
ua |
1 ua = 1.495 978 706 91(6)×1011 m |
| Unités naturelles (u.n.) | |||
| vitesse | unité naturelle de vitesse (vitesse de la lumière dans le vide) |
co |
299 792 458 m s-1 |
| action | unité naturelle d’action (constante de Planck réduite) |
ℏ |
1.054 571 68(18)×10-34 Js |
| masse | unité naturelle de masse (masse de l’électron) |
me |
9.109 382 6(16)×10-31 kg |
| temps, durée | unité naturelle de temps |
ℏ/(meco2) |
1.288 088 667 7(86)×10-21 s |
| Unités atomiques (u.a.) | |||
| charge | unité atomique de charge (charge électrique élémentaire) |
e |
1.602 176 53(14)×10-19 C |
| masse | unité atomique de masse (masse de l’électron) |
me |
9.109 382 6(16)×10-31 kg |
| action | unité atomique d’action (constante de Planck réduite) |
ℏ |
1.054 571 68(18)×10-34 Js |
| longueur | unité atomique de longueur bohr (rayon de Bohr) |
ao |
0.529 177 210 8(18)×10-10 m |
| énergie | unité atomique d’énergie, hartree (énergie de Hartree) |
Eh |
4.359 744 17(75)×10-18 J |
| temps, durée | unité atomique de temps |
ℏ/Eh |
2.418 884 326 505(16)×10-17 s |
6°/ Autres unités en dehors du SI :
|
Grandeur |
Nom de l’unité |
Symbole de l’unité |
Valeur en unités SI |
| pression | bar | bar | 1 bar = 0.1 MPa = 105 Pa |
| millimètre de mercure | mmHg | 1 mmHg ≈ 133.322 Pa | |
| longueur | angström | Å | 1 Å = 0.1 nm = 10-10 m |
| distance | mille marin | M | 1 M = 1852 m |
| superficie | barn | b | 1 b = 100 fm2 = 10-28 m2 |
| vitesse | noeud | kn | 1 kn = (1852/3600) m s-1 |
| logarithme d’un rapport | néper | Np | |
| bel | B | ||
| décibel | dB |
7°/ Unités en dehors du SI associées aux systèmes d’unités CGS :
|
Grandeur |
Nom de l’unité |
Symbole de l’unité |
Valeur en unités SI |
| énergie | erg |
erg |
1 erg = 10-7 J |
| force | dyne |
dyn |
1 dyn = 10-5 N |
| viscosité dynamique | poise |
P |
1 P = 1 dyn s cm-2 = 0.1 Pa s |
| viscosité cinématique | stokes |
St |
1 St = 1 cm2 s-1 = 10-4 m2 s-1 |
| luminance lumineuse | stilb |
sb |
1 sb = 1 cd cm-2 = 104 cd m-2 |
| éclairement lumineux | phot |
ph |
1 ph = 1 cd sr cm-2 = 104 lx |
| accélération | gal |
Gal |
1 Gal = 1 cm s-2 = 10-2 m s-2 |
| flux d’induction magnétique | maxwell |
Mx |
1 Mx = 1 G cm2 = 10-8 Wb |
| induction magnétique | gauss |
G |
1 G = 1 Mx cm-2 = 10-4 T |
| champ magnétique | œrsted |
Oe |
1 Oe ≙ (103/4π) A m-1 |
8°/ Préfixes et multiples SI :
| Facteur | Nom | Symbole | Facteur | Nom | Symbole | |
|
101 |
déca |
da |
10-1 |
déci |
d |
|
|
10² |
hecto |
h |
10-2 |
centi |
c |
|
|
103 |
kilo |
k |
10-3 |
milli |
m |
|
|
106 |
méga |
M |
10-6 |
micro |
μ |
|
|
109 |
giga |
G |
10-9 |
nano |
n |
|
|
1012 |
téra |
T |
10-12 |
pico |
p |
|
|
1015 |
péta |
P |
10-15 |
femto |
f |
|
|
1018 |
exa |
E |
10-18 |
atto |
a |
|
|
1021 |
zetta |
Z |
10-21 |
zepto |
z |
|
|
1024 |
yotta |
Y |
10-24 |
yocto |
y |
Les noms et les symboles des multiples et sous-multiples décimaux de l’unité de masse sont formés par l’adjonction de noms de préfixes au mot ‘gramme’ et de symboles de ces préfixes au symbole de l’unité ‘g’.
Les préfixes SI représentent strictement des puissances de 10. Ils ne doivent pas être utilisés pour exprimer des puissances de 2 (par exemple, un kilobit représente 1000 bits et non 1024 bits). Les noms et symboles des préfixes correspondant à 210, 220, 230, 240, 250, et 260 sont, respectivement: kibi, Ki; mébi, Mi; gibi, Gi; tébi, Ti; pébi, Pi; et exbi, Ei. Ainsi, par exemple, un kibioctet s’écrit: 1 KiB = 210 B = 1024 B, où B désigne l’octet. Bien que ces préfixes n’appartiennent pas au SI, ils doivent être utilisés en informatique afin d’éviter un usage incorrect des préfixes SI.
III°/ L’histoire du mètre :
Le , l’Académie royale des sciences de Paris adopte le rapport d’une commission composée de Condorcet, Borda, Laplace et Monge qui préconise de choisir, comme base du nouveau système universel de poids et mesures, la dix-millionième partie du quart du méridien terrestre passant par Paris. Condorcet propose que l’on ne mesure pas le quart de méridien tout entier, mais seulement, sur le 45° parallèle et au niveau de la mer, l’arc de 9,5° qui sépare Dunkerque de Barcelone.
A cet effet, deux scientifiques Français Delambre et Méchain, sont chargés de la mesure précise de l’arc de méridien de Dunkerque à Barcelone. La triangulation s’opère de à fin , avec 115 triangles et deux bases : celle de Melun et celle de Perpignan. Les angles sont mesurés avec la méthode du cercle répétiteur de Borda.Le mètre est né est mesure
|

|
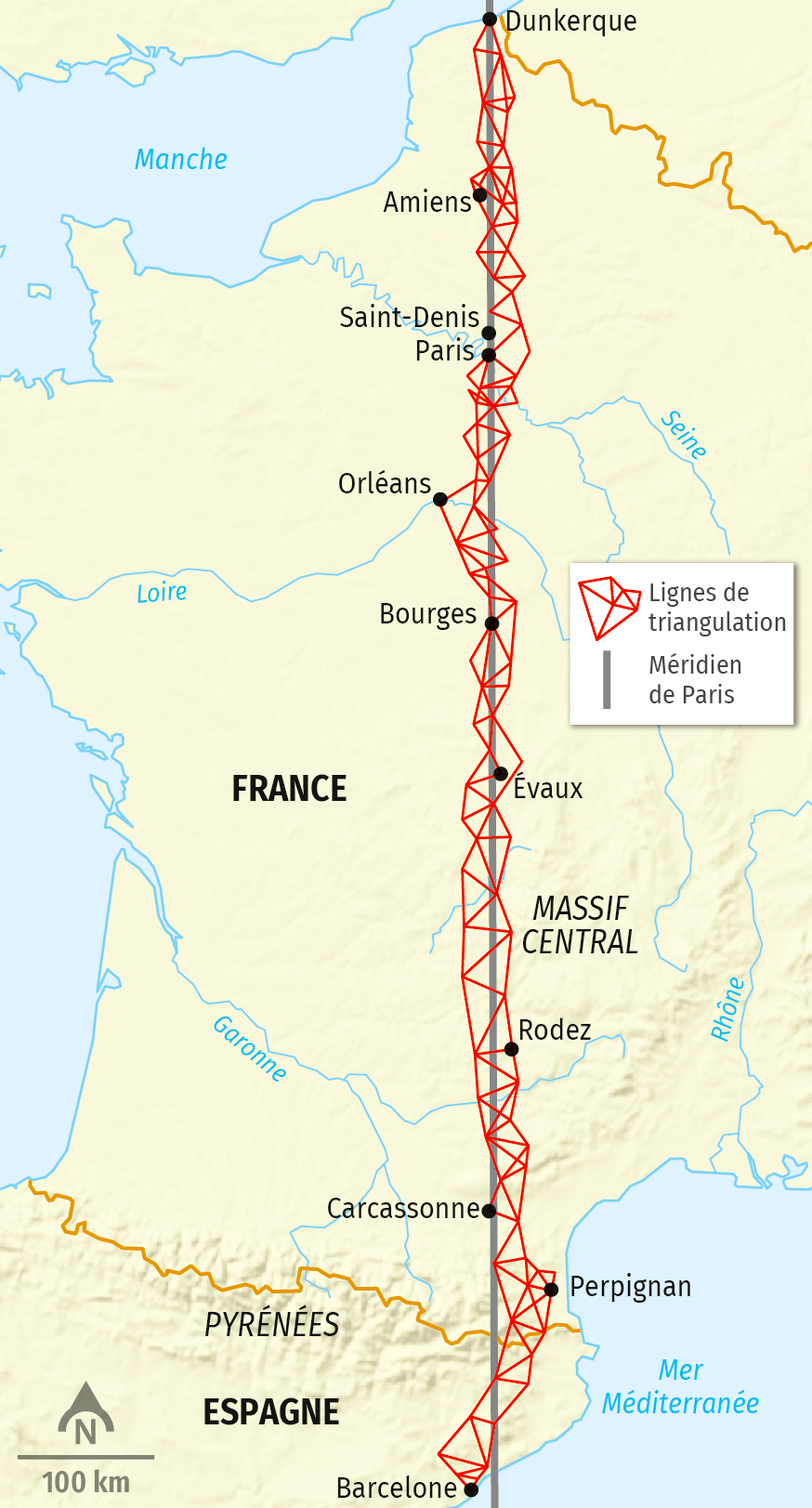 |

Méthode de mesure par triangulation : La méthode consiste à mesurer précisément une base AB, puis on vise un point C éloigné et on mesure les angles \widehat{CAB} et \widehat{CBA}. On en déduit la distance BC en utilisant les relations du triangle. Celle-ci constitue alors la base d’un nouveau triangle dont le sommet est D. |
Voici une excellente vidéo intitulée « Un mètre pour mesurer le monde », qui retrace la grande épopée de la création du mètre durant la révolution Française.
Bibliographie:
- « The International System of Units (SI). » Bureau International des Poids et Mesures. 30 Nov 2010. <http://www.bipm.org/en/si/>.
- « The International System of Units from NIST. » Oct 2000. National Institute of Standards and Technology. 30 Nov 2010. <http://physics.nist.gov/cuu/Units/>.
- « Le Système international d’unités (SI). » Bureau International des Poids et Mesures. 30 Nov 2010. <http://www.bipm.org/fr/si/>.
- http://www.periodni.com/fr/systeme_international_d_unites.html#table_1
Utilité d’uniformiser les mesures :
En 1998 la NASA envoie la sonde Mars Climate Orbiter pour étudier la météorologie de la planète Mars. Malheureusement la sonde se place sur une orbite trop basse et est détruite en traversant à grande vitesse la partie supérieure de l’atmosphère martienne. En effet, les valeurs communiquées au moteur de freinage étaient exprimées en Livre-force par seconde (unités anglo-saxonne) et non en Newton par seconde (Système international d’unités SI). Sachant que 1 Livre-force par seconde représente 4,5 Newton par seconde, la vitesse était 4,5 fois trop grande, le moteur de freinage sous-estime les données d’un facteur 4,5.