VIII°/ Les triangles mystérieux : 64 = 65 = 66 = 67 = 68 = 69

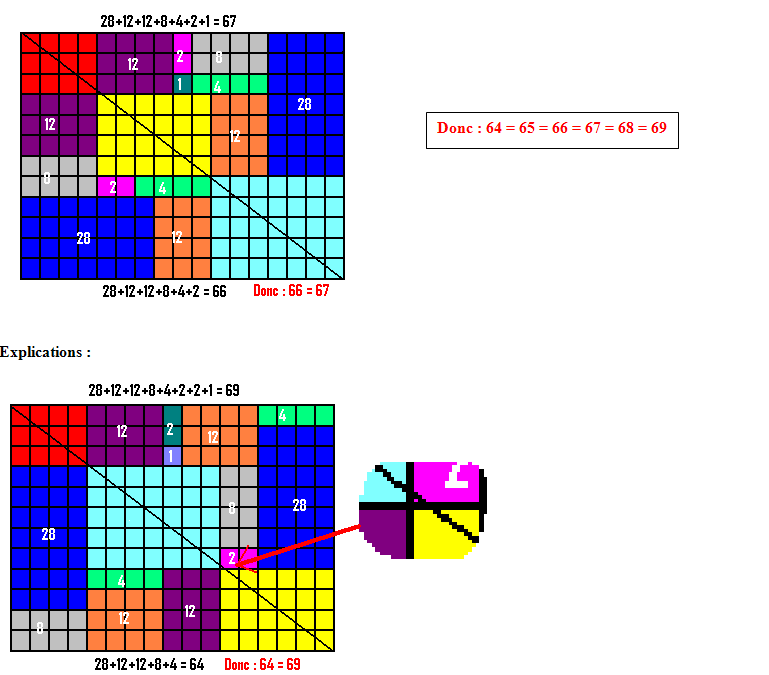
I°/ 64 = 65 = 66 = 67 = 68 = 69 :
II°/ 45 = 49 :
III°/ 104 = 105 : Le rectangle d’Harry Langman
IV°/ Le puzzle magique : Le triangle de Gardner
V°/ Le paradoxe de Curry :
VI°/ Le puzzle de Circée ou le paradoxe des aires :
VII°/ Le trangram :

I°/ 64 = 65 = 66 = 67 = 68 = 69 :

C’est Sam Loyd qui, au début du siècle, démontre que 64 = 65 ( et donc par soustraction que 0 = 1 ? ).

Jean Brette a développé cette idée pour le compte des Editions Kangourou, sur des rectangles de 17 par 12.

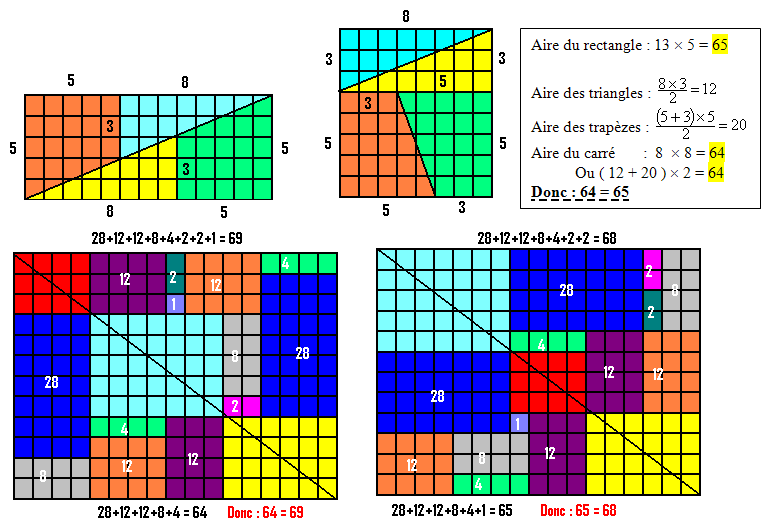
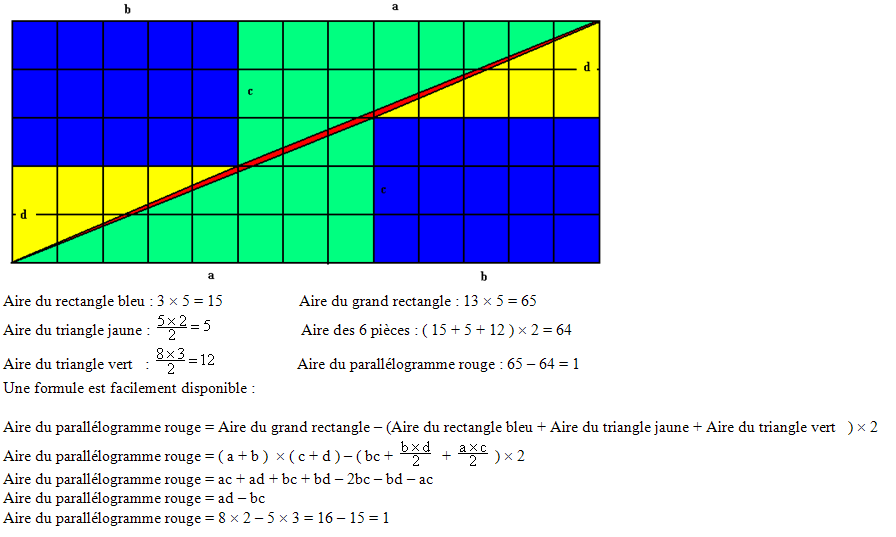
Regardons ce qui se passe avec 2 triangles rectangles. Si les hypoténuses ne sont pas alignées, les aires sont différentes si l’on intervertit les triangles.

Cette différence est l’aire du parallélogramme rouge, qui est facile à calculer :

II°/ 45 = 49 :

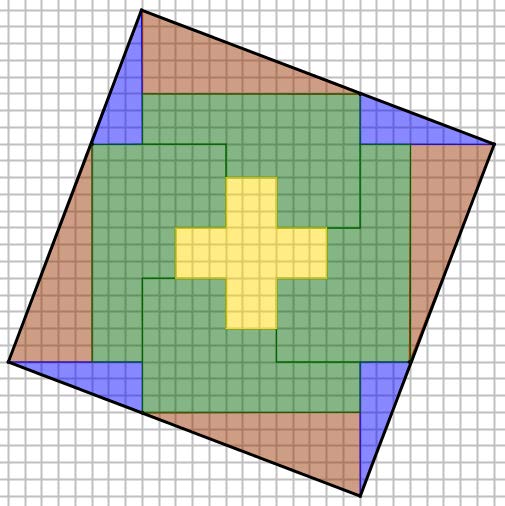
Voici un puzzle de la croix avec 13 pièces.	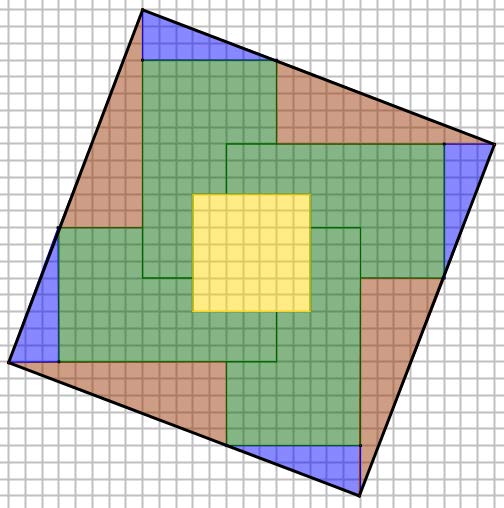Avec les mêmes 13 pièces, voici un carré.
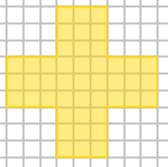
Cependant la croix fait 45 unités d’aire.	Et le carré 45 unités d’aire. Il en manque 4 !!!

Là encore on a l’impression que les triangles sont semblables, mais …

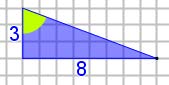
tan(angle vert) = 8/3 ≈ 2,66°

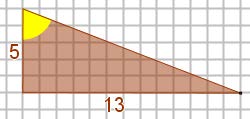
tan(angle jaune) = 13/5 = 2,6°

Fichier à télécharger.

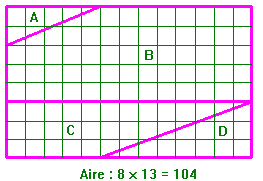
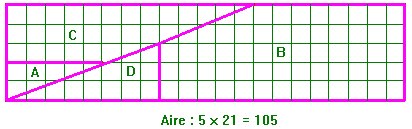
III°/ 104 = 105 : Le rectangle d’Harry Langman

Voilà la solution :

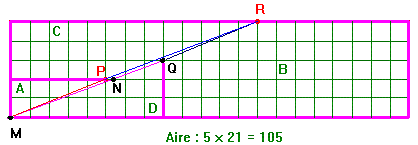
Regardons bien la figure :  les points P et N ne sont pas confondus contrairement à ce que l’on semble penser dans la figure reconstituée. La figure C est en fait le polygone limité par PR et non NR. De même la figure A est limitée par MP et non MN. La figure B elle est limitée par QR et D par MQ qui passe par N.
Nous avons donc un trou constitué du polygone MPRQN dont l’aire est exactement égale à une unité. Comme cette unité est dispersée en longueur elle est bien sûr quasiment invisible.
On peut aussi expliquer le résultat en observant que les points M, P et R ne sont pas alignés. C’était donc une erreur de reconstitution. C’est difficile à voir (déplacez la droite ci-dessus), car en fait les segments MP et QR sont parallèles mais pas avec PQ… d’où un résultat aberrant.

Nous retrouvons une fois de plus, les nombres 5, 8, 13, 21 qui font partie de la suite de Fibonacci. Si nous choisissons deux nombres consécutifs de la suite pour longueur et largeur d’un rectangle et ceux qui l’encadrent pour l’autre rectangle nous obtenons alternativement un gain ou une perte de 1 unité.
Ces gains et pertes se traduisent par la formation ou le chevauchement d’un léger espace vide d’autant plus petit que les nombres seront grands.

IV°/ Le puzzle magique : Le triangle de Gardner

L’inventeur du beau paradoxe qui suit est Paul Curry, magicien amateur de New York. En 1953 il eut l’idée de découper une figure et d’en réarranger les morceaux de telle manière que la nouvelle figure soit identique à l’originale, mais avec un trou à l’intérieur de son périmètre.

Un triangle rectangle avec un trou de 1 unité.
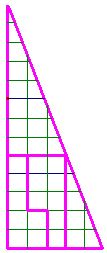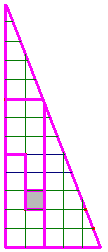Un triangle isocèle avec un trou de 2 unités.

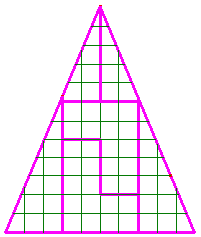V°/ Le paradoxe de Curry :

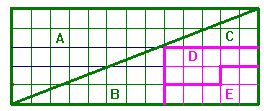
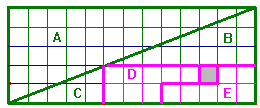
Nous découpons le grand rectangle en 5 morceaux.
Et nous observons un trou d’une unité à droite…

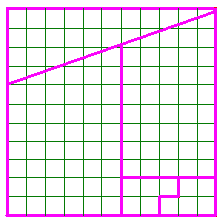
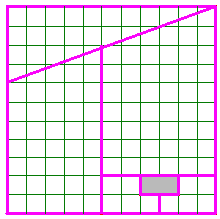
Les variantes les plus élégantes du paradoxe de Curry sont des carrés qui restent des carrés après le réarrangement des morceaux produisant le trou. En voici quelques unes.

Avec un trou de 2 unités dans un carré de 11 sur 11.
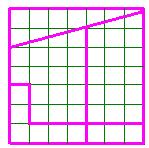
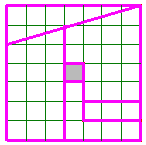
Avec un trou de 1 unité dans un carré de 7 sur 7.

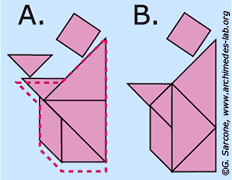
VI°/ Le puzzle de Circée ou le paradoxe des aires :

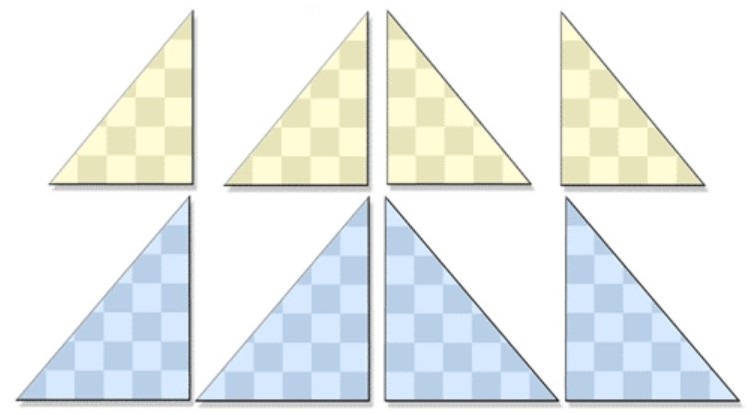Pouvez-vous fabriquer des carrés à l’aide de ces 8 triangles rectangles que l’on appelle le puzzle de Circée ? Cela ne semble pas très compliqué, mais essayez de trouver toutes les configurations possibles.

Voici les 5 possibilités :

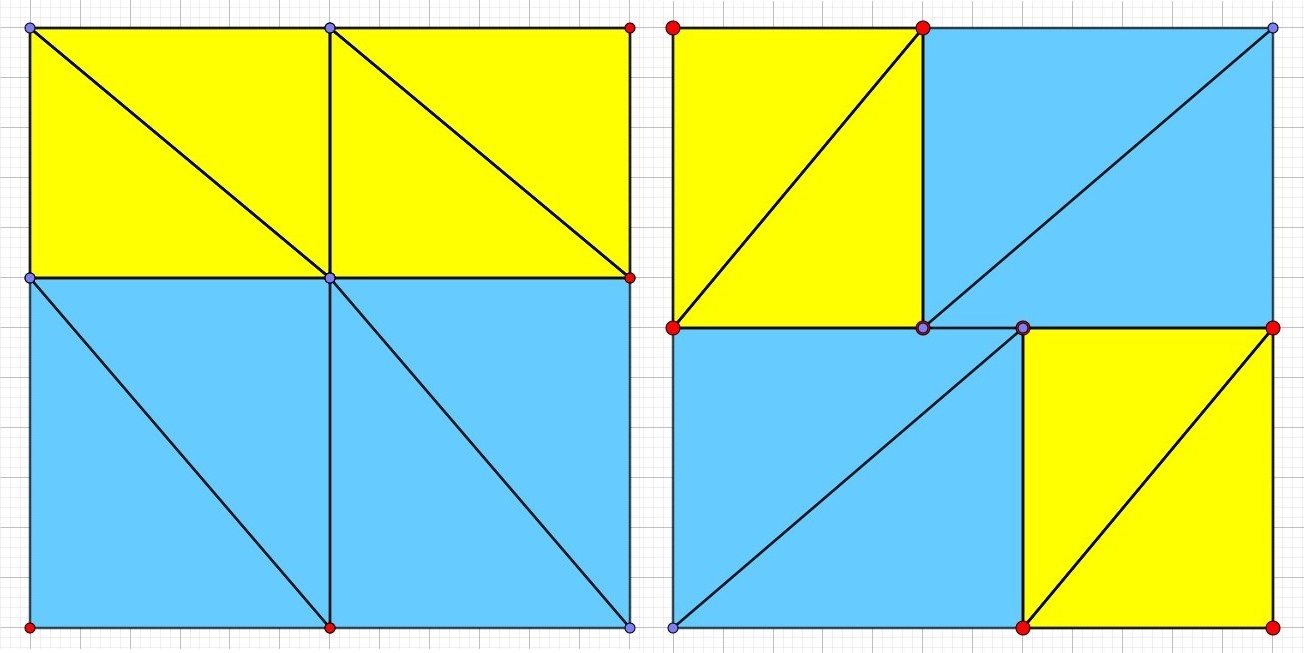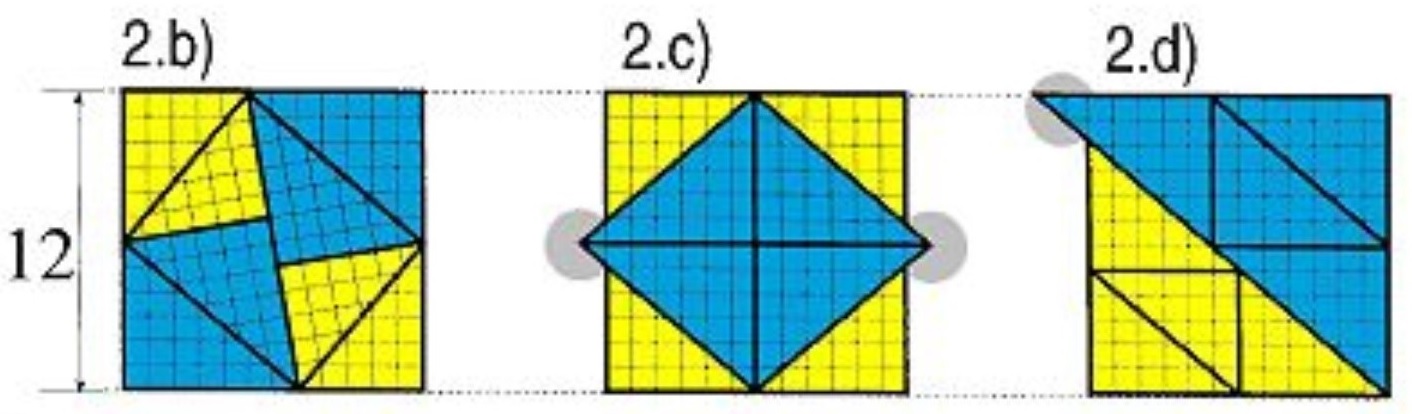Pour ces deux solutions, il n’y a pas de problèmes.	La figure 2.a) semble être un carré, mais ce n’est pas du tout le cas ! Les figures 2.b) et 2.c) sont bien des carrés mais avec des éléments triangulaires saillants, qui augmente l’aire du carré !

L’explication

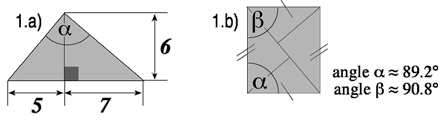	Lorsque l’on place côte à côte deux triangles rectangles du puzzle de Circée, un petit et un grand, on obtient un autre triangle plus grand qui semble être un triangle rectangle. Mais en réalité, d’après les mesures de l’illustration 1.a), l’angle a ne peut être égal à 90°. En fait : a = arctan 7/6 + arctan 5/6 = env. 89,2°
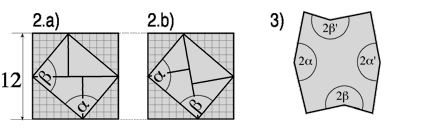	Ainsi, le rectangle inscrit des carrés de la figure 2.a) et 2.b) est en réalité un parallélogramme (voir fig. 1.b), et selon la façon dont celui-ci est orienté, il transforme le carré en un octogone irrégulier (fig. 1.b). .3)!
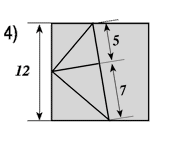	La fig. 4) est une manière visuelle de démontrer que le polygone de la fig. 2.b) ne peut pas être un carré. On le comprend d’un coup d’œil !
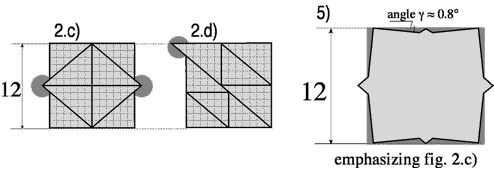	Rassembler des pièces de puzzle triangulaires conduit toujours à des conclusions paradoxales. Les carrés de la fig. 2.c) et 2.d) ont des éléments triangulaires supplémentaires. Leur aire est-elle alors plus grande que celle de la fig. 2.a) ? Comme précédemment, il faut considérer les angles de chaque triangle rectangle qui forme ces carrés. En faisant cela, nous remarquerons facilement que les pentes de l’hypoténuse du petit et du grand triangle rectangle sont légèrement différentes (une différence d’environ 0,8 degrés, visuellement imperceptible). Ainsi, les 8 triangles rectangles ne forment pas exactement un carré et la somme de toutes ces infimes erreurs d’ajustement (zones grises sur la fig. 5) est égale à l’aire des éléments triangulaires saillants. Bref, l’apparition spatiale n’est qu’une illusion !

Voici une application Géogébra pour vous essayer à ce puzzle.

VII°/ Le trangram :

Cliquez ici pour apprendre l’histoire du Tangram et y jouer.

Mais on peut aussi créer de jolis paradoxes.

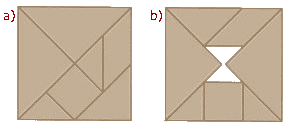	Les deux « carrés » ci-dessous sont constitués des mêmes 7 pièces de tangram. Pourquoi manque-t-il 2 petits triangles dans le second ?
	Ici aussi, ce sont les mêmes 7 pièces qui sont utilisées, et pourtant il y a toujours un petit triangle noir dans la figure rose !

Le truc réside dans le fait que les dimensions des 2 figures respectives sont légèrement différentes. Celles à qui il ‘manque’ une pièce, sont plus saillantes (voir fig. A et B).