|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Maths pour travailler
Des Maths sérieuses mais toujours surprenantes.
V°/ Le jeu de la vie et la probabilité :
La probabilité est basée sur le hasard, ce qui veut dire qu’il est difficile de prévoir le résultat d’une expérience aléatoire.
Par exemple, si on joue à pile ou face et que l’on obtient pile 10 fois consécutivement, tout d’abord cela parait difficile à faire et ensuite la logique voudrait que la probabilité d’obtenir face augmente et soit supérieure à la probabilité d’obtenir pile.
Et bien la probabilité d’obtenir face, tout comme pile, reste toujours de 1/2, quelque soit les lancers précédents. La logique et la probabilité sont quelque fois incompatible.
Pour un mathématicien qui déteste ne pas maitriser les résultats et est allergique aux approximations, on effectueras un très grand nombre d’expérience pour pouvoir affirmer que : pour un très grand nombre de lancer la probabilité d’obtenir pile est de 1/2 ainsi que celle d’obtenir face.
Cependant le hasard peut se montrer bizarre voir artistique.
Index :
I°/ Le jeu de la vie de John Conway : de ScienceEtonnante
II°/ La puissance organisatrice du hasard : de Mickaël Launay
III°/ La fourmi de Langton : de ScienceEtonnante
I°/ Le jeu de la vie de John Conway :
John Conway est un mathématicien célèbre et prolifique qui inventa entre le jeu de la vie.
Le génie de ce jeu réside dans la simplicité des règles qui permet pourtant de fabriquer des effets d’une richesse incroyable.
Sur une feuille quadrillée de la taille que l’on veut, on dispose des cellules qui ne peuvent être que dans 2 états. Si la cellule existe, on dit qu’elle est vivante, sinon elle est morte.
Les règles :
– Une cellule est entourée de 8 cases car on compte aussi les diagonales.
– Une cellule vivante possédant deux ou trois voisines vivantes reste vivante, sinon elle meurt (donc si elle n’a aucune ou une voisine seulement, et si elle a plus de 3 voisines).
– Une cellule morte possédant exactement trois voisines vivantes devient vivante.
 |
1ière étape : – les cases 3 et 6 possèdent 1 seule voisine donc elles meurent. – les cases 4 et 5 possèdent 2 voisines donc elles restent en vie. – les cases 1, 2 ,7 et 8 sont vides (mortes) et possèdent 3 voisines donc elles naissent.2ième étape : – les cases 4 et 5 possèdent 5 voisines donc elles meurent. – les cases 1, 2 ,7 et 8 possèdent 3 voisines donc elles restent en vie. – les cases 3 et 6 sont vides (mortes) et possèdent 3 voisines donc elles naissent.3ième étape : – chaque cases possèdent 2 voisines donc elles restent en vie. |
 |
1ière étape : – les cases 2 et 5 possèdent 3 voisines donc elles restent en vie. – les cases 4 et 6 possèdent 2 voisines donc elles restent en vie. – les cases 1, 3 et 7 sont vides (mortes) et possèdent 3 voisines donc elles naissent.2ième étape : – les cases 3, 5, 6 et 7 possèdent plus de 3 voisines donc elles meurent. – les cases 2, 4 et 9 possèdent 3 voisines donc elles restent en vie. – les cases 1, 8 et 10 sont vides (mortes) et possèdent 3 voisines donc elles naissent.3ième étape : – les cases 2, 4, 8 et 10 possèdent 1 seule voisine donc elles meurent. – les cases 1 et 9 possèdent 2 voisines donc elles restent en vie. – les cases 3, 5, 7 et 11 sont vides (mortes) et possèdent 3 voisines donc elles naissent. |
Il est très simple de coder ses règles et donc de modéliser ce jeu avec un ordinateur. Voici une application pour s’amuser et tester tout plein de situations. Ou ici.
Avec de telles règle aussi simplistes il est peu probable d’obtenir des choses très spectaculaires, et pourtant c’est le cas. On peut en effet obtenir :
On peut trouver à cette adresse, le Wiki du jeu de la vie , qui rassemble tout les motifs extraordinaires obtenus avec ce jeu merveilleux.
Certains motifs sont assez spectaculaires :

Cliquez sur l’horloge pour la voir fonctionner. |
 Le jeu de la vie dans le jeu de la vie. Le jeu de la vie dans le jeu de la vie. |
 |
 |
 |
|
 |
Une vidéo très complète de la chaine Youtube de ScienceEtonnante :
Du chaos émerge l’ordre :
Un autre jeu de ce type : le jeu du chaos. Le principe du jeu du chaos est relativement simple.
| – Placez trois points non alignés, puis choisissez un point A au hasard à l’intérieur du triangle ainsi délimité.
– Choisissez un sommet S du triangle au hasard, par exemple à l’aide d’un dé. – Tracer le milieu du segment qui joint le premier point A au sommet S choisi. – Recommencez le procédé : choisissez un sommet au hasard, notez le milieu, reprenez, et ainsi de suite. |
 |
Du chaos ambiant, du hasard grâce auquel est générée la figure semble pourtant émerger une certaine organisation. Les amateurs de fractale auront sans doute reconnu le triangle de Sirpienski dans notre cas.
Ce qui est fabuleux, c’est que cette forme émerge peu importe le point de départ que l’on choisit : le motif dessiné est « le même ».
II°/ La puissance organisatrice du hasard :
Que pourrait représenté un chemin où on a le choix entre monter de 1 carreau en diagonale ou descendre de 1 carreau en diagonale. Et ceci un nombre infini de fois.
Et dans la deuxième partie de la vidéo, un assemblage de dominos avec une règle très simple qui produit un résultats bluffant et magnifique.
III°/ La fourmi de Langton :
Comment un mouvement très simple mais répéter une infinité de fois peut produire une œuvre magnifique.
IV°/ La 4ième dimension :
Qu’est-ce que c’est que le quatrième dimension, et existe-t’elle ?
Voici une vidéo de la chaine Youtube de Mickaël Launay, qui explique tout de façon claire et artistique.
|
La série de 6 vidéos : La quatrième dimension. |
Voici une série de 9 vidéos : Chaine Youtube de Jos Leys |
|
|
Pour résumer : Une dimension représente un axe qui à deux sens.
Dans une figure qui a 1 dimension, on peut aller à gauche ou à droite (on peut les appeler Longueur).
Dans une figure qui a 2 dimensions, on peut aller à gauche ou à droite (on peut les appeler Longueur) mais aussi en haut et en bas (on peut les appeler largeur).
Dans une figure qui a 3 dimensions, on peut aller à gauche ou à droite (on peut les appeler Longueur) mais aussi en haut et en bas (on peut les appeler largeur) et encore vers l’avant ou l’arrière (on peut les appeler hauteur).
Pour la 4ième dimension il suffit de trouver 2 noms pour désigner les 2 sens supplémentaires. Ce sera Ana et Kapa que l’on peut représenter par des couleurs par exemple.
| Nombre de dimension | 1ière direction | 2ième direction | Représentation |
| 0 | point |  |
|
| 1 | Gauche | Droite |  |
| 2 | Haut | Bas |  |
| 3 | Avant | Arrière |  |
| 4 | Ana | Kapa | 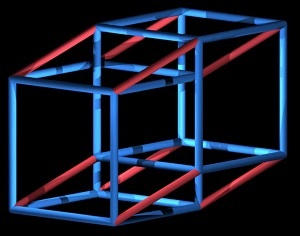 |
Le flexaèdre et les hexaflexagones :
Construction d’un flexaèdre dont la géométrie est inspirée de l’hypercube.
Le flexaèdre :Télécharger le patron et construire 12 tétraèdres non réguliers : |
|
Le tri-hexaflexagones : hexaflexagones à 3 faces.Télécharger le patron et suivre la vidéo pour la construction. Le site de El JJ pour d’autres constructions. |
|
Le tétra-tétraflexagone :
|
|
Le tetra-hexaflexagones : hexaflexagones à 4 faces.Télécharger le patron et suivre la vidéo pour la construction. |
|
L’hexa-tétraflexagone :
|
II°/ Le nombre Pi : Un nombre célèbre et mystérieux.
I°/ Son utilité :
A°/ La géométrie :
B°/ La probabilité :
C°/ Les nombres premiers entre eux :
D°/ Les suites :
E°/ L’analyse :
F°/ La Bible :
G°/ Quelques belles formules faisant intervenir \pi :
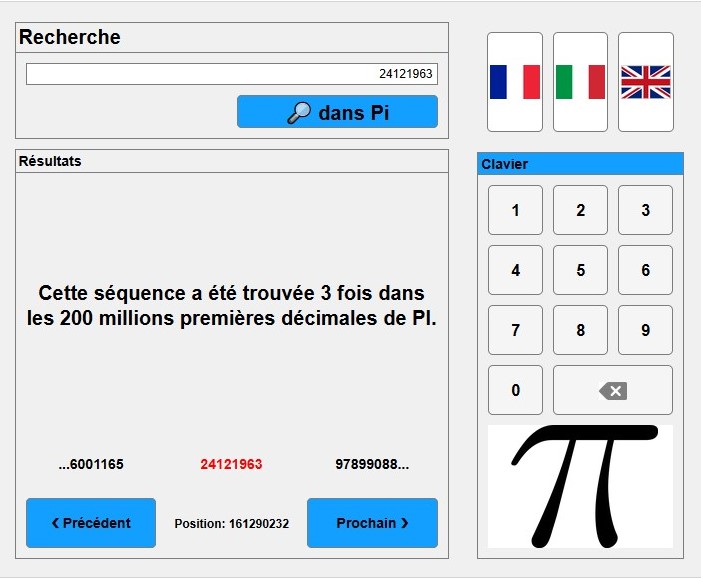
II°/ Son écriture : Pi-Search le site pour trouver des décimales
III°/ Son calcul :
A°/ A Babylone :
B°/ En Égypte :
C°/ En Grèce :
1°/ Démonstration de la formule de l’aire du disque :
2°/ Calcul du nombre \pi :
D°/ Époque moderne :
E°/ Le nombre Tau :
IV°/Quelques histoires originales sur [latex] \pi [/latex] :
A°/ un nombre univers :
B°/ L’Indiana pi bill :
C°/ La pyramide de Khéops :
D°/ Amusons nous :
I°/ Son utilité :
On retrouve le nombre \pi un peut partout dans les Mathématiques.
A°/ La géométrie :
Son utilité principale est de calculer la circonférence du cercle, l’aire du disque et le volume de la boule, mais aussi les ellipses.
| Circonférence du cercle = | 2 \pi R |
| Aire du disque = | \pi R^{2} |
| Volume boule = | \frac{4}{3} \pi R^{3} |
Une définition simple de est que ce nombre représente le périmètre d’un cercle de diamètre un.
Perimetre_{cercle}= 2\pi R = \pi \times D = \pi\times 1 = \pi
B°/ Les probabilités :
Au 18ième siècle, un grand mathématicien français du nom de George Buffon a réalisé l’expérience suivante. Il lance des aiguilles sur un parquet composés de lames rectangulaires. Si la longueur des aiguilles est égale à la largeur des lames de parquet, combien a t’on de chance qu’il y ai une aiguille qui se trouve à l’intersection de 2 lames et non à l’intérieur d’une lame ?
Il a démontrer que cette probabilité était de \frac{2} {\pi}
C°/ Les nombres premiers entre eux :
Un nombre premier est un nombre qui n’est divisible que par 1 ou par lui-même. Par exemple :
12 n’est pas premier car 12 = 3 x 4
23 est premier car 23 = 1 x 23 et c’est tout.
Deux nombres sont premiers entre eux s’ils n’ont pas de diviseur commun autre que 1, donc s’ils ne sont pas dans la même table de multiplication. Par exemple :
15 et 6 ne sont pas premiers entre eux car ils sont divisibles par 3.
15 et 4 sont premiers entre eux car ils ne sont divisibles que par 1.
Les mathématiciens se sont amusés a déterminer quelle proportion de couple de nombre était premiers entre eux (oui ils ont des jeux bizarre !!).
Cette proportion est de \frac{\pi^{2}}{6}
D°/ Les suites :
Si on ajoute tous les inverses des carrés on obtient un nombre qui sera égal à 1,644… qui représente le nombre \frac{\pi^{2}}{6}
\sum_{i=1}^{\infty }\frac{1}{i^{2}}=\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}...=\frac{\pi ^{2}}{6}
E°/ L’analyse :
C’est la branche des mathématiques qui traite explicitement de la notion de limite, que ce soit la limite d’une suite ou la limite d’une fonction.
Une définition du nombre \pi est :
\pi est le plus petit nombre réel a > 0 tel que cos(a) = -1
F°/ La Bible :
Dans le passage de la Bible 1. Rois 7.23 : « Il fit la Mer en métal fondu, de dix coudées de bord à bord, à pourtour circulaire de 5 coudées de hauteur ; un fil de 30 coudées en mesurait le tour »
Traduction : dix coudées de bord à bord donc un diamètre de 10 coudées
30 coudées en mesurait le tour donc un périmètre de 30 coudées
Donc pour dieu : \pi = \frac{30}{10} = 3
G°/ Quelques belles formules faisant intervenir \pi : La source
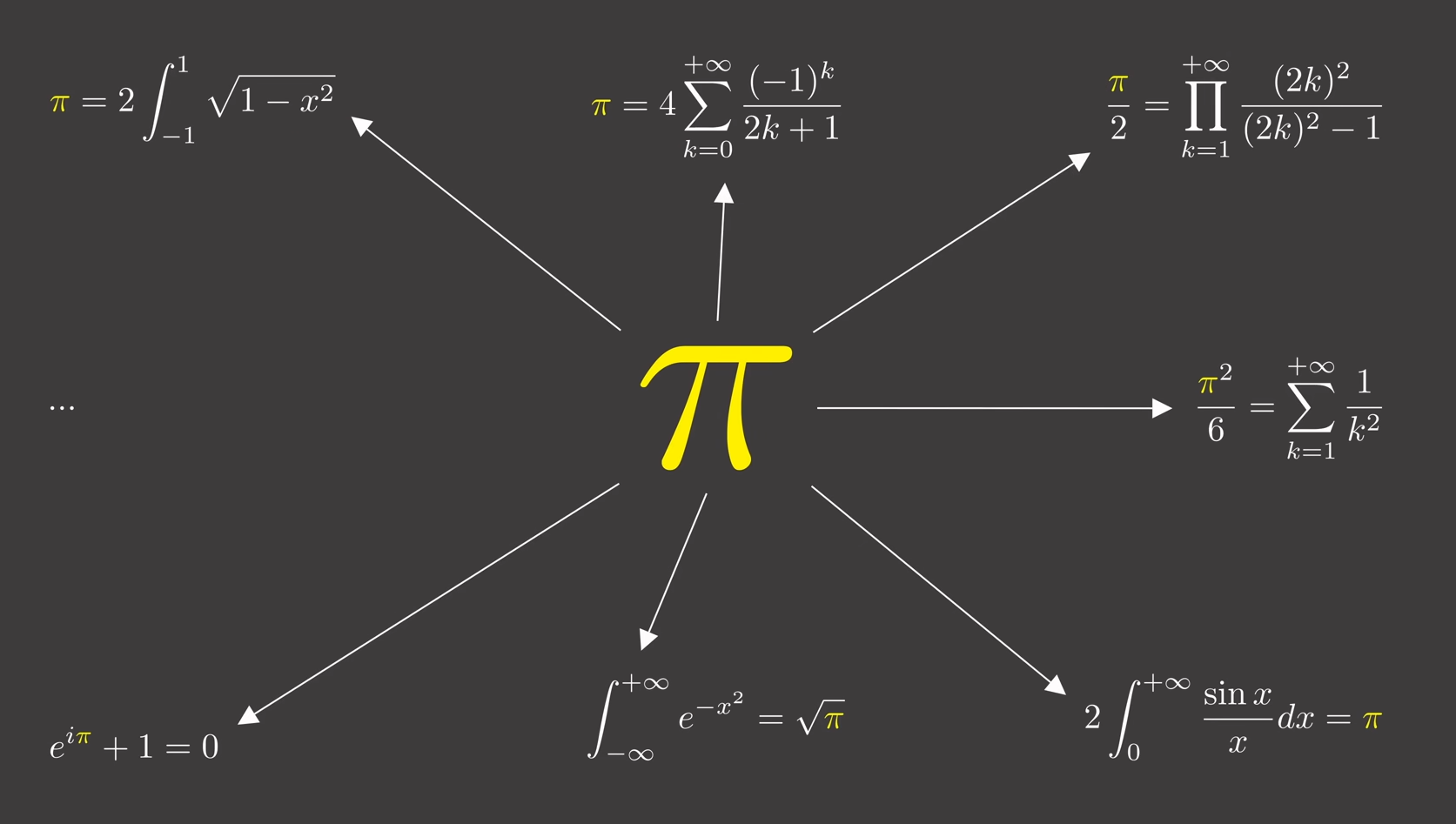




|
Formule liant \pi , la suite de Fibonacci et la trigonométrie : \Huge \frac{\pi}{4}=\sum_{i=1}^{+\infty}arctan\left(\frac{1}{F_{2i+1}}\right) |
II°/ Son écriture :
Sa grande particularité est qu’il possède un nombre infini de décimales. Il fait parti des nombres irrationnels qui ne peuvent donc pas s’écrire sous la forme d’une fraction de 2 nombres entiers.
Mais attention, c’est l’écriture décimale de \pi qui est infinie, ou son nombre de décimale, ce n’est pas le nombre \pi lui-même. En effet, un cercle de diamètre une unité a un périmètre de \pi unité, et c’est bien une longueur finie.
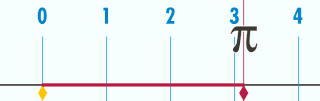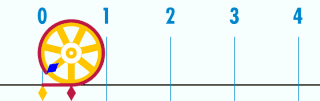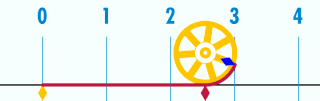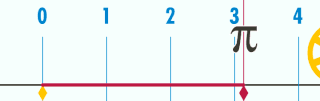
Vers -230 av JC, Archimède est capable de donner le nombre au centième prés avec sa méthode des polygones inscrits et circonscrits au cercle. Un peu plus tard,en 1420 à Samarcande en Perse, Al Kashi est capable de calculer 14 décimales de \pi.
Nous en connaissons à présent en 2 000 milliards fin 2016.
Voici les décimales de \pi au cours des âges (Pour plus de détail)
| Date | Mathématicien et lieu | Décimales |
| -2500 | Grande pyramide de Gizeh (Égypte) | \frac{22}{7}\approx 3,142857 \ 142857 \ 142857 ... |
| -2000 | Tablette Babylonienne découverte en 1936 | \frac{25}{8}= 3,125 |
| -1650 | Le papyrus Rhind (Égypte) Approximation du cercle par un octogone régulier. |
\left (\frac{16}{9}\right )^{2} \approx 3,16 |
| -500 | La Bible I Roi 7:23 :Il fit la mer de fonte. Elle avait dix coudées d’un bord à l’autre, une forme entièrement ronde, cinq coudées de hauteur, et une circonférence que mesurait un cordon de trente coudées. |
3 |
| -400 | Platon (Grèce) \pi = \sqrt{2}+\sqrt{3} | 3.15 |
| -250 | Archimède (Grèce) Approximation du cercle par un polygone régulier à 96 côtés. |
\frac{223}{74}< \pi < \frac{22}{7} |
| 5 | Liu Xin (Chine) | 3.1457 |
| 429–500 | Zu Chongzhi | 6 décimales : \frac{355}{113}\approx 3,14159292. |
| 499 | Aryabhata (Inde) | 3 décimales : \frac{62 832}{20 000}= 3,14175 |
| 1120 | Fibonacci (Léonard de Pise) (Italie) | 3,141818 |
| 1592 | François Viete (Un des premiers produits infinis de l’histoire). | 9 décimales : \pi = 2 \times \frac{2}{\sqrt{2}} \times \frac{2}{\sqrt{2+\sqrt{2}}} \times \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}} \times ... |
| 1650 | William Brouncker (1620-1687) | \frac{\pi}{4 }=\frac{1}{1+\frac{1^{2}}{2+\frac{3^{2}}{2+\frac{5^{2}}{2+...}}}} |
| 1665 | Isaac Newton (Angleterre) | 16 décimales : \pi = \frac{3\sqrt{3}}{4}+24\left ( \frac{1}{3 \times 2^{2}} -\frac{1}{5 \times 2^{5}} -\frac{1}{7 \times 2^{9}} - \frac{1}{9 \times 2^{12}} ... F ...\right ) \\ F=\frac{1\times3\times...\times(2n-1) }{2\times4\times...\times(2n+2)} \times \frac{1}{2n+5} \times \frac{1}{2^{2n+4}} |
| 1706 | William Jones (Pays de Galles). Il utilise pour la première fois le symbole \pi | |
| 1719 | Thomas Fantet de Lagny (France) | 112 décimales |
| 1761 | Johann Heinrich Lambert (Allemagne)Il prouve que \pi est irrationnel, il suggère qu’il est transcendant sans le prouver. | |
| 1788 | \sum_{n=1 }^{\infty}\frac{1}{n^{2}}=\frac{\pi ^{2}}{6} = \frac{1}{1^{2}} +\frac{1}{2^{2}}+\frac{1}{3^{2}}... \\ \frac{\pi}{2}=\frac{3 \times 5\times7\times9\times11\times.. }{2\times6\times8\times10\times12\times...} | |
| 1913 |
\pi = \lim_{k\rightarrow \infty }2^{k} \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}} Avec k la quantité de radicaux. \frac{9}{5}+\sqrt{\frac{9}{5}}=3,141 64...=\pi+0,000 05...
|
|
| 1946 | Ferguson. Il utilise pour la première fois un calculateur informatique, une calculatrice de bureau. | 620 décimales |
| 1949 | John Wrench (États-Unis) Le premier à utiliser un ordinateur (l’ENIAC) en 70 heures. | 2037 décimales |
| 1973 | Jean Guilloud et Martin Bouyer (France)Sur un CDC 7600 en 23 h 20 min | 1 001 250 décimales |
| 1989 | Gregory V. Chudnovsky & David V. Chudnovsky (États-Unis)Sur un CRAY-2 & IBM 3090/VF | 480 000 000 décimales |
| 2011 | Alexander J. Yee et Shigeru. (Japon) | 10 000 milliards de décimales |
| 2016 | Peter Trueb | 22 x 1012 décimales |
Voici tout plein d’autre formules plus jolies les unes que les autres !!!!
Voici les 2400 premières décimales de pi :
3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362 440 656 643 086 021 394 946 395 224 737 190 702 179 860 943 702 770 539 217 176 293 176 752 384 674 818 467 669 405 132 000 568 127 145 263 560 827 785 771 342 757 789 609 173 637 178 721 468 440 901 224 953 430 146 549 585 371 050 792 279 689 258 923 542 019 956 112 129 021 960 864 034 418 159 813 629 774 771 309 960 518 707 211 349 999 998 372 978 049 951 059 731 732 816 096 318 595 024 459 455 346 908 302 642 522 308 253 344 685 035 261 931 188 171 010 003 137 838 752 886 587 533 208 381 420 617 177 669 147 303 598 253 490 428 755 468 731 159 562 863 882 353 787 593 751 957 781 857 780 532 171 226 806 613 001 927 876 611 195 909 216 420 198 938 095 257 201 065 485 863 278 865 936 153 381 827 968 230 301 952 035 301 852 968 995 773 622 599 413 891 249 721 775 283 479 131 515 574 857 242 454 150 695 950 829 533 116 861 727 855 889 075 098 381 754 637 464 939 319 255 060 400 927 701 671 139 009 848 824 012 858 361 603 563 707 660 104 710 181 942 955 596 198 946 767 837 449 448 255 379 774 726 847 104 047 534 646 208 046 684 259 069 491 293 313 677 028 989 152 104 752 162 056 966 024 058 038 150 193 511 253 382 430 035 587 640 247 496 473 263 914 199 272 604 269 922 796 782 354 781 636 009 341 721 641 219 924 586 315 030 286 182 974 555 706 749 838 505 494 588 586 926 995 690 927 210 797 509 302 955 321 165 344 987 202 755 960 236 480 665 499 119 881 834 797 753 566 369 807 426 542 527 862 551 818 417 574 672 890 977 772 793 800 081 647 060 016 145 249 192 173 217 214 772 350 141 441 973 568 548 161 361 157 352 552 133 475 741 849 468 438 523 323 907 394 143 334 547 762 416 862 518 983 569 485 562 099 219 222 184 272 550 254 256 887 671 790 494 601 653 466 804 988 627 232 791 786 085 784 383 827 967 976 681 454 100 953 883 786 360 950 680 064 225 125 205 117 392 984 896 084 128 488 626 945 604 241 965 285 022 210 661 186 306 744 278 622 039 194 945 047 123 713 786 960 956 364 371 917 287 467 764 657 573 962 413 890 865 832 645 995 813 390 478 027 590 099 465 764 078 951 269 468 398 352 595 709 825 822 620 522 489 407 726 719 478 268 482 601 476 990 902 640 136 394 437 455 305 068 203 496 252 451 749 399 651 431 429 809 190 659 250 937 221 696 461 515 709 858 387 410 597 885 959 772 975 498 930 161 753 928 468 138 268 683 868 942 774 155 991 855 925 245 953 959 431 049 972 524 680 845 987 273 644 695 848 653 836 736 222 626 099 124 608 051 243 884 390 451 244 136 549 762 780 797 715 691 435 997 700 129 616 089 441 694 868 555 848 406 353 422 072 225 828 488 648 158 456 028 50
Pour savoir comment on les calcule, cliquez ici.
Même si ce n’est pas encore démontré, le nombre est considéré comme un nombre univers, c’est à dire que c’est un nombre réel dans les décimales duquel on peut trouver n’importe quelle succession de chiffres de longueur finie. Vous pouvez ainsi vérifier sur cette page, si votre date de naissance ou votre numéro de téléphone est présent dans les décimales de
. En fait on peut tout trouver dans les décimales de , à partir du moment ou on le transforme en suite de nombre. Par exemple une photo est une succession de pixel codés par un nombre représentant sa couleur, vous pouvez donc trouver n’importe quelle photo. Si on remplace les lettres par leur rang dans l’alphabet, on peut trouver n’importe quel texte dans les décimales de (Maths sera codé par M = 13, a = 1, t = 20, h = 8, s = 13 et 13120813 ce retrouve au rang 29247731) !!!!
Il existe heureusement des moyens mnémotechniques de retenir ces décimales : il s’agit de retenir des phrases dont les mots ont autant de lettres que les décimales successives (un mot de dix lettres donne la décimale 0) de .
Voici par exemple un poème connu permettant de trouver les 127 premières décimales :
Que j’aime à faire apprendre ce nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur ?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l’orbe calculée approchera ;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.
A propos : biographie de Pythagore
Et bien sûr, cette méthode est aussi utilisée à l’étranger : voici quelques exemples
Anglais
|
Yes, I have a great statement to relate. |
| May I have a large container of coffee. | |
| How I wish I could recollect of circle round The exact relation Archimede unwound. |
|
| How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics ! | |
| How I wish I could enumerate Pi easily, since all these horrible mnemonics prevent recalling any of pi’s sequence more simply. (ici, « pi’s » compte pour un mot) |
|
| But a time I spent wandering in bloomy night ; Yon tower, tinkling chimewise, loftily opportune. Out, up, and together came sudden to Sunday rite, The one solemnly off to correct plenilune. |
|
Allemand
|
Dir, o Held, o Alter Philosoph, du Reisen-Genie ! Wie, viele Tausende bewundern Geister Himmlisch wie du und Göttlich ! Noch reiner in Aeonen Wird das uns strahlen, Wie im lichten Morgenrot ! |
| Wie ? O ! Dies p Macht ernstlich so vielen viele Müh ! Lernt immerhin, Jünglinge, leichte Verselein, Wie so zum Beispiel dies dürfte zu merken sein ! |
|
Espagnol
|
Con 1 palo y 5 ladrillos se pueden hacer mil cosas. |
| Sol y Luna y cielo proclaman al divino autor del cosmo. | |
Portugais
|
Sou o medo e temor constante do menino vadio. |
Danois
|
Eva, o lief, o zoete hartedief uw blauwe oogen zyn wreed bedrogen. |
Albanais
|
Kur e shoh e mesoj sigurisht. |
La même technique est utilisée pour retenir d’autres nombres célèbres :
- Les trois journées de 1830 ont renversé 89 : 1/pi = 0,3183098…
- Tu aideras à rappeler ta quantité à beaucoup de docteurs amis : e = 2,7182818284…
- Gamma pourras retenir, si à Euler penses chaque fois. Constante immortelle d’Euler, vas-tu toujours rester timidement cachée ? : G = 0,5772156649015328606…
- O nombre d’élégance ! Toi, toi, grandiose, étonnant : 1,61803398, le nombre d’or.
III°/ Son calcul :
A°/ A Babylone:
On ne connait pas l’origine du nombre \pi , mais il est déjà présent 2000 av JC. Bien entendu on ne l’appelle pas encore Pi mais il est donné comme le rapport du périmètre du cercle sur son diamètre.
Le première trace de \pi apparaît sur la tablette de Suse datant de -1680 av JC.
 |
La tablette donne l’aire de 2/25 pour un cercle de périmètre 1. Perimetre_{cercle} = 2\pi R = 1 \ donc \ R = \frac{1}{2\pi }\\Aire_{cercle} = \pi R^{2} = \frac{2}{25} =0,08 \ donc \ \pi\times \frac{1}{4\pi ^{2}} = 0,08 \\ donc \ \pi = \frac{1}{4\times 0,08}=\frac{25}{8}=3.125Une très bonne approximation. |
B°/ En Égypte :
Il y a 4000 ans, en Égypte, il existait une méthode pour assimiler l’aire d’un disque à celle d’un carré.
Cette « recette » magique fut trouver sur le Papyrus Rhind écrit par le scribe Ahmès. Il s’agit d’une « recette » car, si elle permet de trouver une approximation au 100ième de \pi , il n’y a pas de démonstration et on ne parle pas encore du nombre \pi .
Voici ce quelle raconte : l’aire d’un disque de 9 unités de diamètre est égale à l’aire d’un carré de 8 unités de côté.
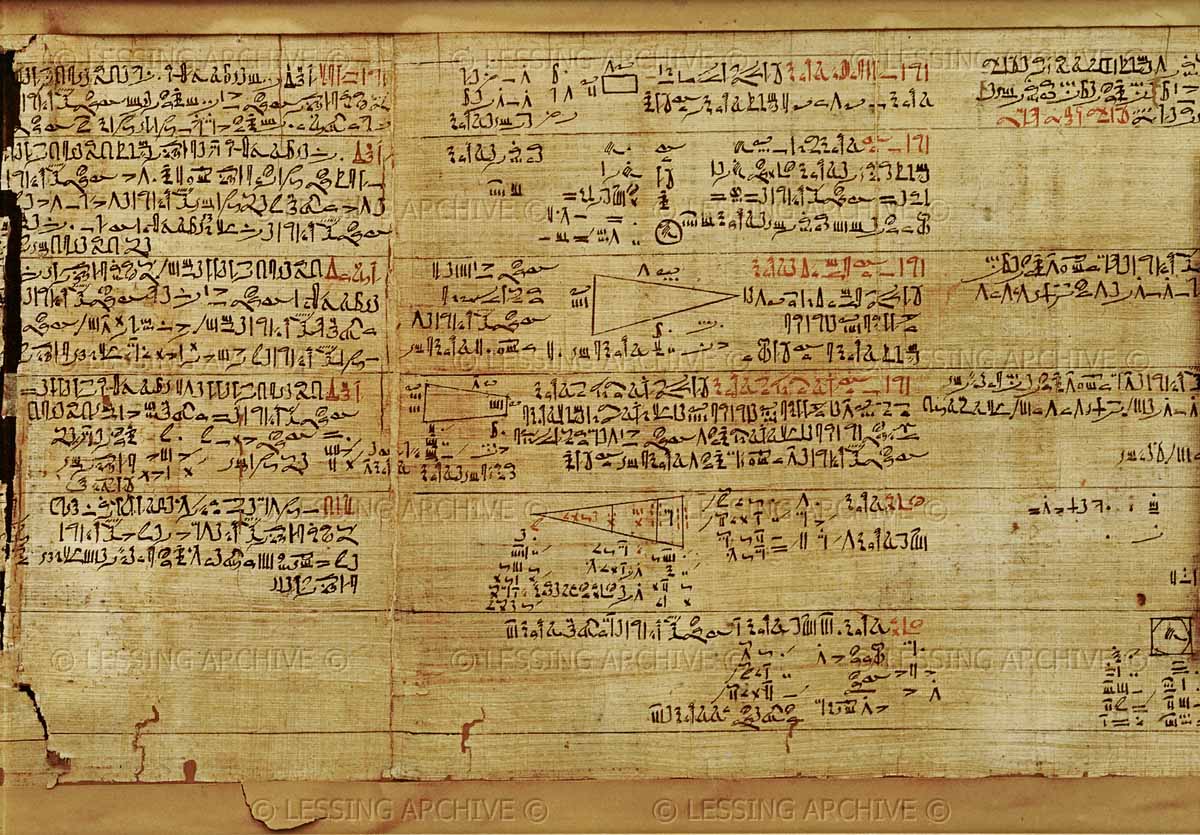 |
Le Papyrus de Rhind est un papyrus de l’ancienne Égypte, datant de la XVème dynastie (vers 1680-1620 avant J.-C.), trouvé à Thèbes en 1858 dans les ruines d’un petit monument proche du Ramesseum par l’égyptologue écossais Alexander Henry Rhinds. |
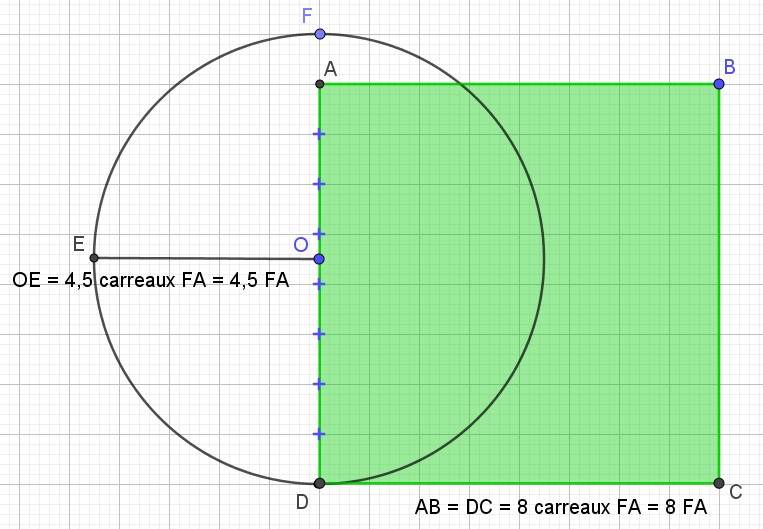 |
Dans un cercle de centre O et de rayon OE = 1 unité, on découpe le diamètre DF en 9 morceaux FA.
Le carré ABCD de côté AB = 8FA aura la même aire que le cercle. Aire Disque = Aire Carré
3,16 au lieu de 3,14 cela fait une erreur de moins de 2 centièmes, ce qui est exceptionnel pour l’époque. |
C°/ En Grèce :
Archimède en -250 av JC sera le premier à faire une démonstration.
1°/ Démonstration de la formule de l’aire du disque :
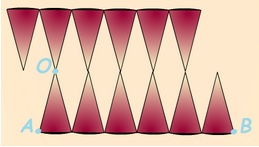
Archimède assimile l’aire d’un disque à celle d’un polygone ayant beaucoup de cotés, inscrit au disque.
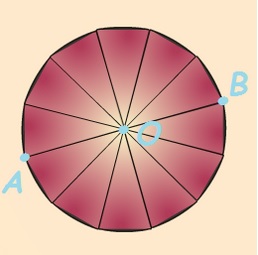 |
 |
 |
| Découpons un disque de centre O et de rayon R = OA en 12 parts égales. |
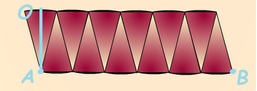
On déplie le disque. | En réassemblant les parts on fabrique un parallélogramme. |
La longueur AB représentant le demi-périmètre du cercle :
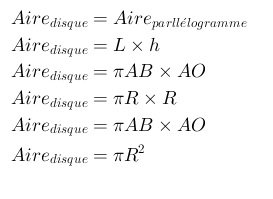 |
Bien entendu la longueur AB n’est pas vraiment un segment, surtout si on découpe le disque en
seulement 12 parts. Mais plus le nombre de parts sera grand et plus se sera exact. Si on découpe le disque en un nombre infini de parts, alors les arcs de cercles noirs s’aplaniront, AB tendra vers un segment, raisonnement sera correct et la formule du disque sera bien |
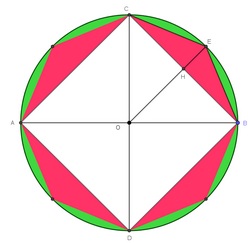
Calculons l’erreur que l’on commet en assimilant AB à un segment, c’est à dire les surfaces noires des figures au-dessus :
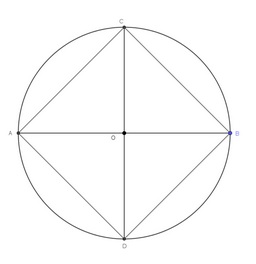 |
 |
 |
 |
|
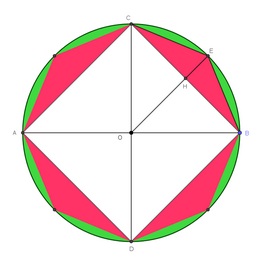
Commençons par découper un cercle |
La zone verte représente la différence entre l’aire du disque et celle du carré. L’erreur est importante. |
Si on découpe en 8, la partie verte est plus petite. L’aire de l’octogone se rapproche de celle du disque. |
L’erreur verte crée par l’octogone est-elle plus petite que celle, rouge, crée par le carré. C’est le cas car si on rassemble les 2 secteurs circulaires verts ils sont plus petits que l’erreur rouge. On gagne la surface bleue. |
2°/ Calcul du nombre \pi :
– Méthode des polygones d’Archimède : il faut encadrer un cercle de rayon 1 par des polygones inscrits et circonscrits et calculer leurs périmètres.
Dans un cercle de diamètre 1 :
Donc :
|
|
|
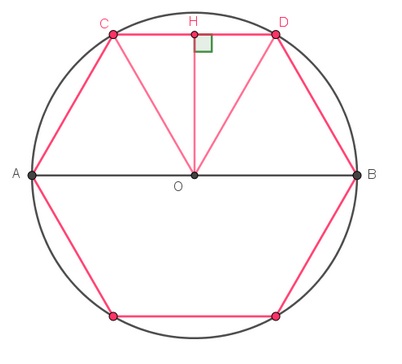
| Traçons l’hexagone inscrit dans le cercle, avec n = 6. | Traçons l’hexagone circonscrit au cercle, avec n = 6. |
| Dans le triangle COH rectangle en H.
|
Dans le triangle BOE rectangle en B.
|
Le nombre sera donc obtenu par l’encadrement suivant :
Pour n = 6 on aura : 3,10582854123025 < < 3,21539030917347
Bien entendu il s’agit d’une approximation, mais si on renouvelle la démonstration en doublant le découpage du cercle (6, 12, 24, 48, 96…), au bout de 96 parts Archimède a obtenu l’encadrement suivant :
3,141 031 951 < \pi < 3,1427146
pour une valeur exacte de \pi = 3,141 592 653. L’erreur est seulement de moins de 1 millième !!!! 2 siècles avant JC c’est impressionnant.
|
|
|
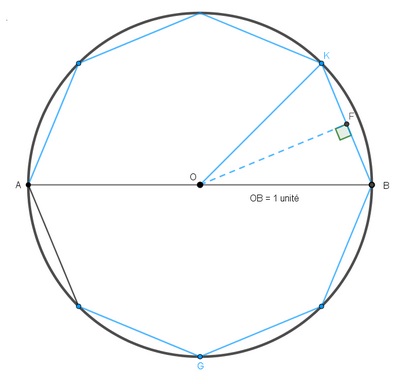
– Variante de la méthode d’Archimède, mais en calculant les aires : il faut encadrer un disque de rayon 1 par des polygones inscrits et circonscrits et calculer leurs aires.
Dans un disque de diamètre 1 :
 |
 |
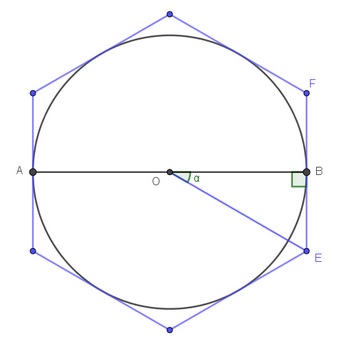
| Traçons l’octogone inscrit dans le cercle, avec n = 4. | Traçons l’octogone circonscrit au cercle, avec n = 4. |
| Dans le triangle BOF rectangle en F.
sin \ \widehat{BOF}=\frac{FB}{BO} =\frac{FB}{1}=FB = \frac{FO\times n \times KB}{2} |
Dans le triangle GRO rectangle en G.
|
Le nombre sera donc obtenu par l’encadrement suivant :
Pour n = 4 on aura : 2,82842712474619 < \pi < 3,31370849898476
Là encore, il s’agit d’une approximation, mais si on renouvelle la démonstration en doublant le découpage du disque (4, 8, 16, 32, 64, 128….), au bout de 128 parts on obtient l’encadrement suivant :
3,14033115695475 < \pi < 3,14222362994246
Voici un fichier Excel qui donne des encadrements jusqu’à plusieurs millions de parts. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page Excel ci-dessous pour l’ouvrir dans Microsoft Office Online).
Plus simplement, on peut démontrer que 3<\pi<4 en encadrant un cercle de rayon 1 entre un hexagone de côté 1 et un carré de côté 2 :
Il existe de nombreuse technique pour calculer le nombre \pi , mais il y en a une qui est très visuelle et qui utilise les fractions continues :
\pi = 3,14159265358979323846... = 3 + 0,14159265358979323846... = 3 + \frac{1}{\frac{1}{0.14159265358979323846...}} = 3 + \frac{1}{7,06251331...} \approx 3 + \frac{1}{7} = \frac{22}{7} = 3,1428 cad \pi à 2 décimales près.
Mais on peut aller plus loin :
\pi = 3 + \frac{1}{7,06251331...} = 3 + \frac{1}{7+\frac{1}{15,9965...}} = 3 + \frac{1}{7+\frac{1}{15 + 0,9965...}} = 3 + \frac{1}{7+\frac{1}{15 + \frac{1}{1+ 0,00341..}}} \approx 3 + \frac{1}{7+\frac{1}{15 + \frac{1}{1}}} = \frac{355}{113} cad \pi à 6 décimales près.
On peut ainsi, de proche en proche et au prix de très, très nombreux calculs, découvrir les décimales de \pi . Mais j’avais promis une méthode visuelle. La voici :
 |
 |
 |
| Plaçons un point vert sur un repère d’origine O, et construisons ses symétriques successifs par la rotation de centre O et d’angle \pi degrés. On observe la spirale de \pi . | Si on construit en rouge la même rotation mais d’angle \frac{22}{7} on remarque que les points sont assez proches. | Et si on construit en bleu la même rotation mais d’angle \frac{355}{113} , les points bleus et verts sont confondus. \frac{355}{113} est donc une très bonne approximation de \pi . |
|
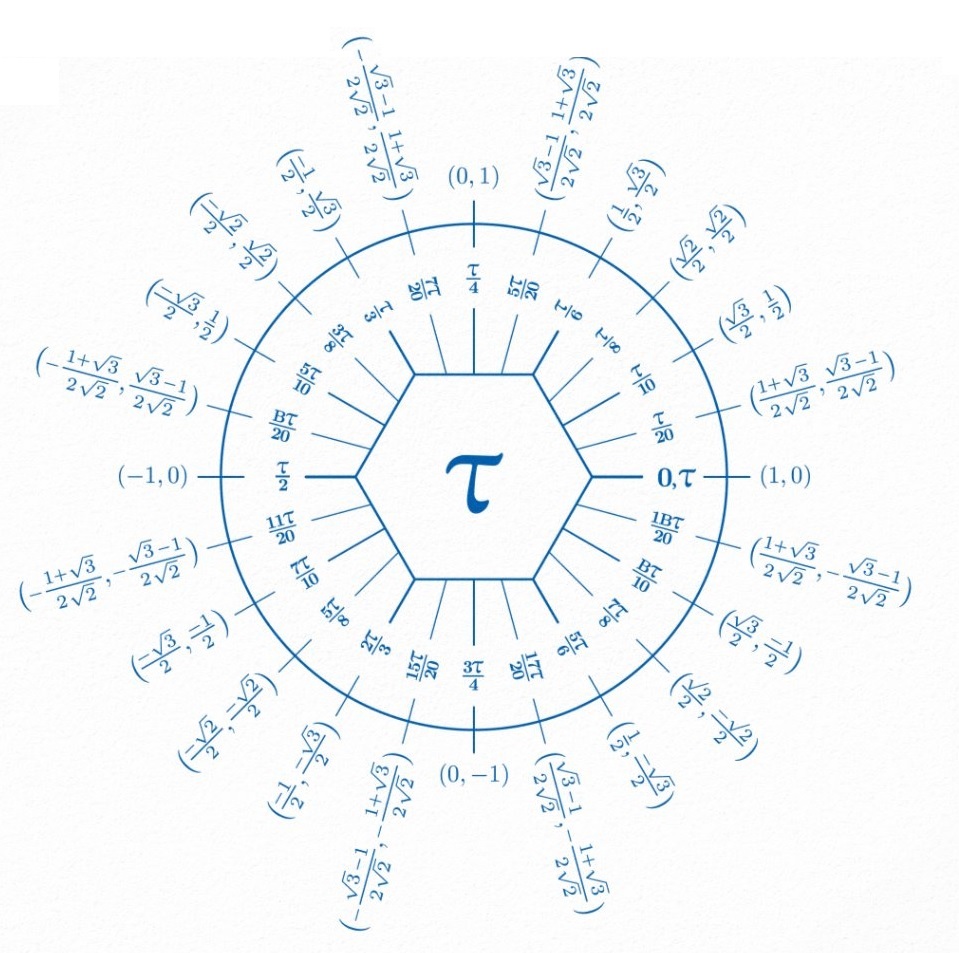
Tau est le jumeau maléfique de Pi (π). Il représente deux fois la constante Pi (3.14…), s’écrit en notation anglophone 6.28, ce qui correspond au 28 juin. Michael Hartl, éducateur et physicien théorique, cherche depuis 2010 à faire accepter cette constante —et le «jour de Tau»— à la place de Pi —et du «jour de Pi» le 14 mars— dans les milieux mathématiques. Pour lui, il serait préférable de dire que le périmètre d’un cercle est égal à Tau fois le rayon. Voici le cercle trigonométrique utilisant Tau pour donner les coordonnées des points du cercle. |
 |
IV°/ Quelques histoires originales sur \pi :
A°/ \pi est un nombre univers :
On considère qu’il n’y a aucune suite de nombre périodique dans les décimales de \pi et que l’on peut y trouver n’importe quelle suite de chiffre. On appelle ce genre de nombre des nombres univers. On a pas encore réussit à démontrer que \pi en était un, mais cela semble certain.
Par exemple, le nombre 210615, qui est la date de naissance de Napoléon, se trouve à la position 91698. Ce nombre apparaît 225 fois dans les 200 millions premiers chiffres de \pi .
On peut numériser n’importe quelle image, musique, film ou programme, et bien ils sont tous dans les décimales de \pi .
Voici deux sites où vous amuser à retrouver votre propre date de naissance, votre poids en grammes ou tous ce que vous voulez : The Pi-Search Page ou sur le site du Palais de la découverte.
Il existe d’autres nombres univers :
- la constante de Champernowne est 0,12345678910111213141516…, c’est à dire, le nombre dont le développement décimal est la suite des nombres entiers collés les uns aux autres. Un outil pour rechercher une suite de chiffre.
- la constante de Copeland-Erdös, qui vaut 0,235711131719… (la suite des nombres premiers les uns à la suite des autres).
B°/ L’Indiana pi bill :
En 1897, l’état de l’indiana vote la loie n°246 qui décrète que le nombre \pi sera désormais égal à 3,2 sur la proposition d’un médecin et mathématicien amateur Edwin J. Goodwin. La quadrature du cercle était démontrée ….
Fort heureusement cette la loi n’a jamais été adoptée, grâce à l’intervention d’un professeur de mathématiques, Clarence Abiathar Waldo (en), qui était accidentellement présent dans l’assemblée.
 |
 |
| Dessin paru dans le Rock Island Argus du 6 mars 1897, se moquant du projet. | Schéma avec certaines dimensions qui peut être vu dans les œuvres d’Edwin J. Goodwin. Elles sont totalement fausses. |
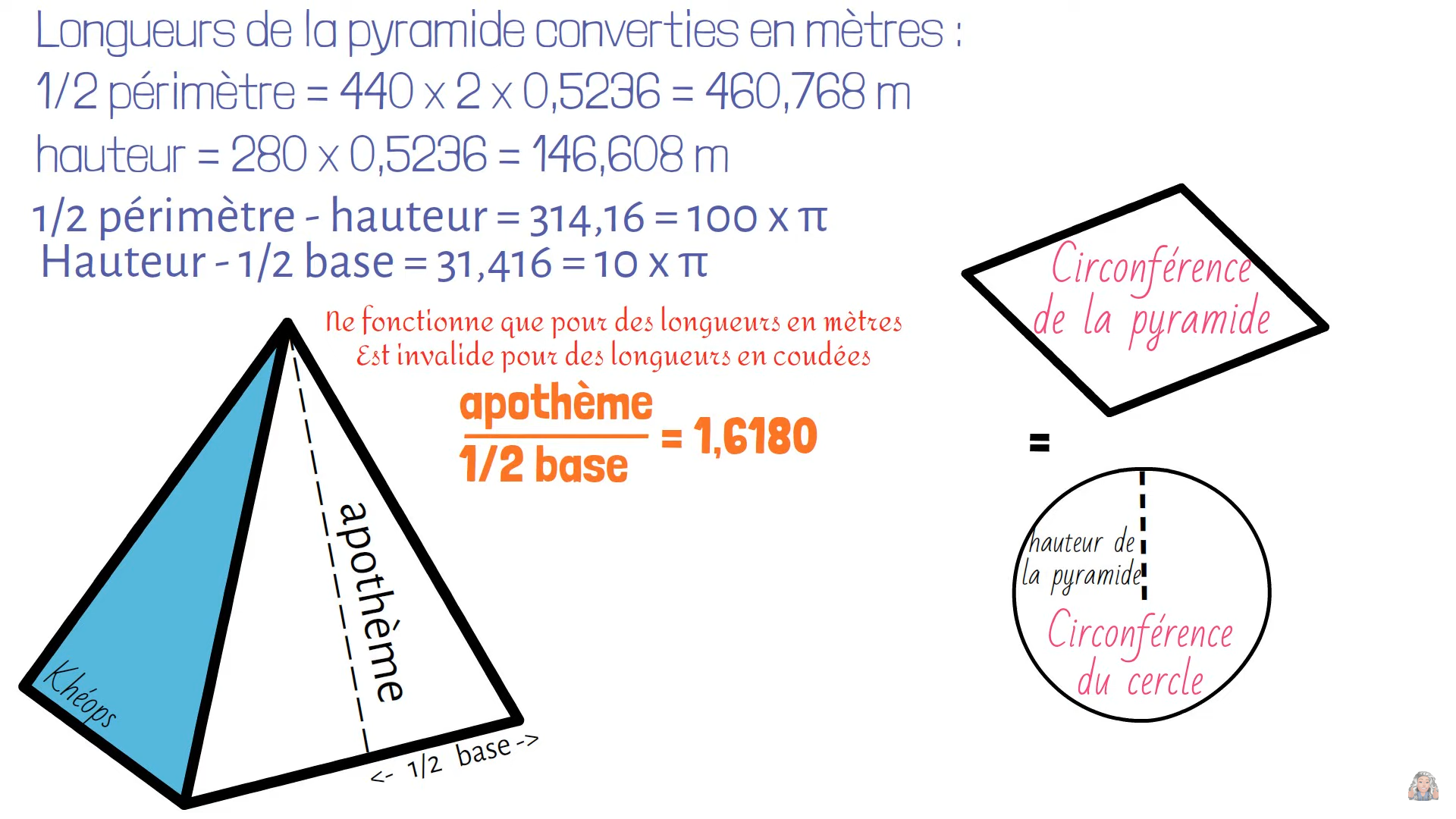
En triturant toutes les mesures de la pyramide, on peut retrouver le nombre d’or dans de nombreux rapport. De là à affirmer que c’était voulu par les bâtisseurs …
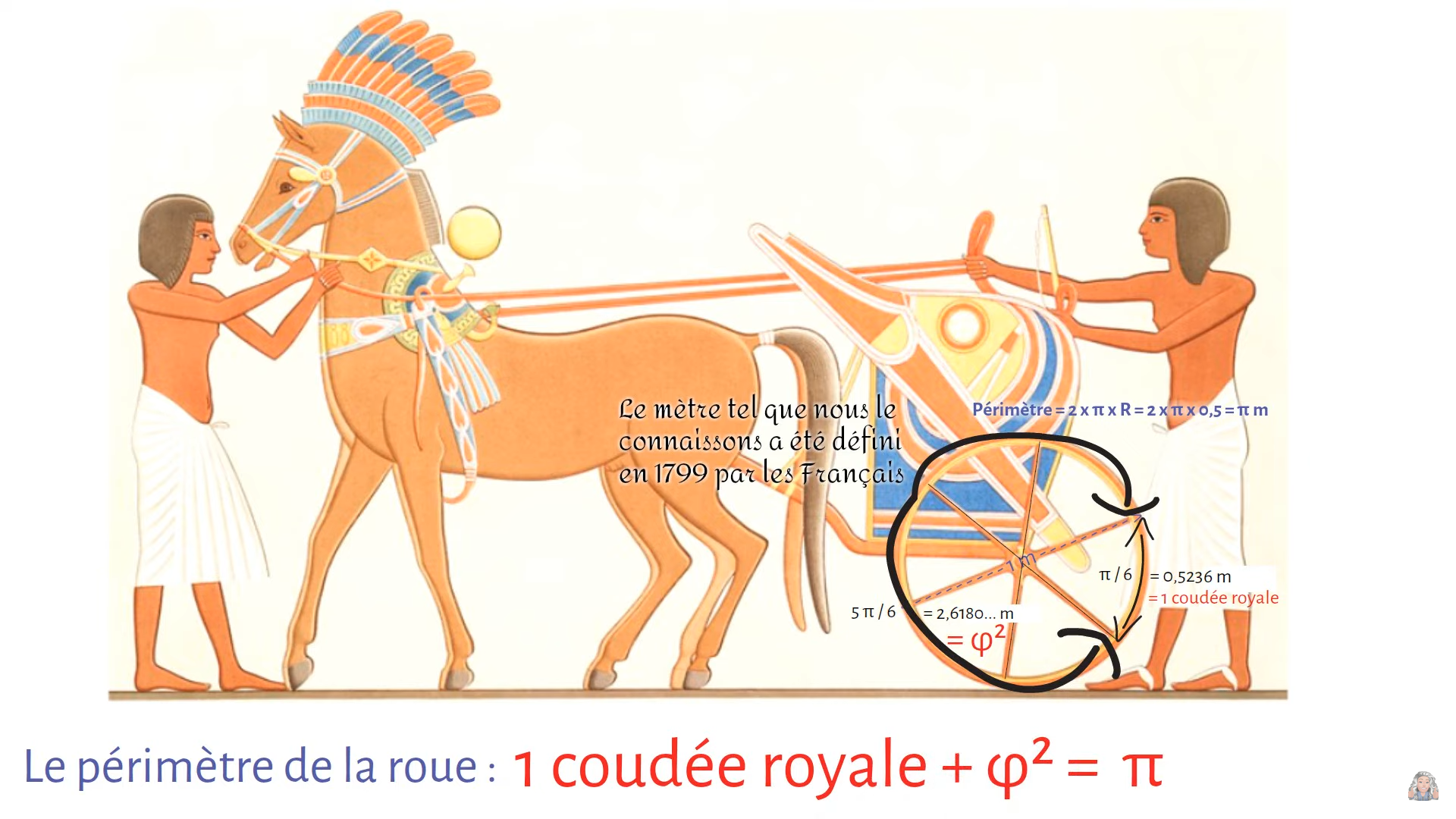
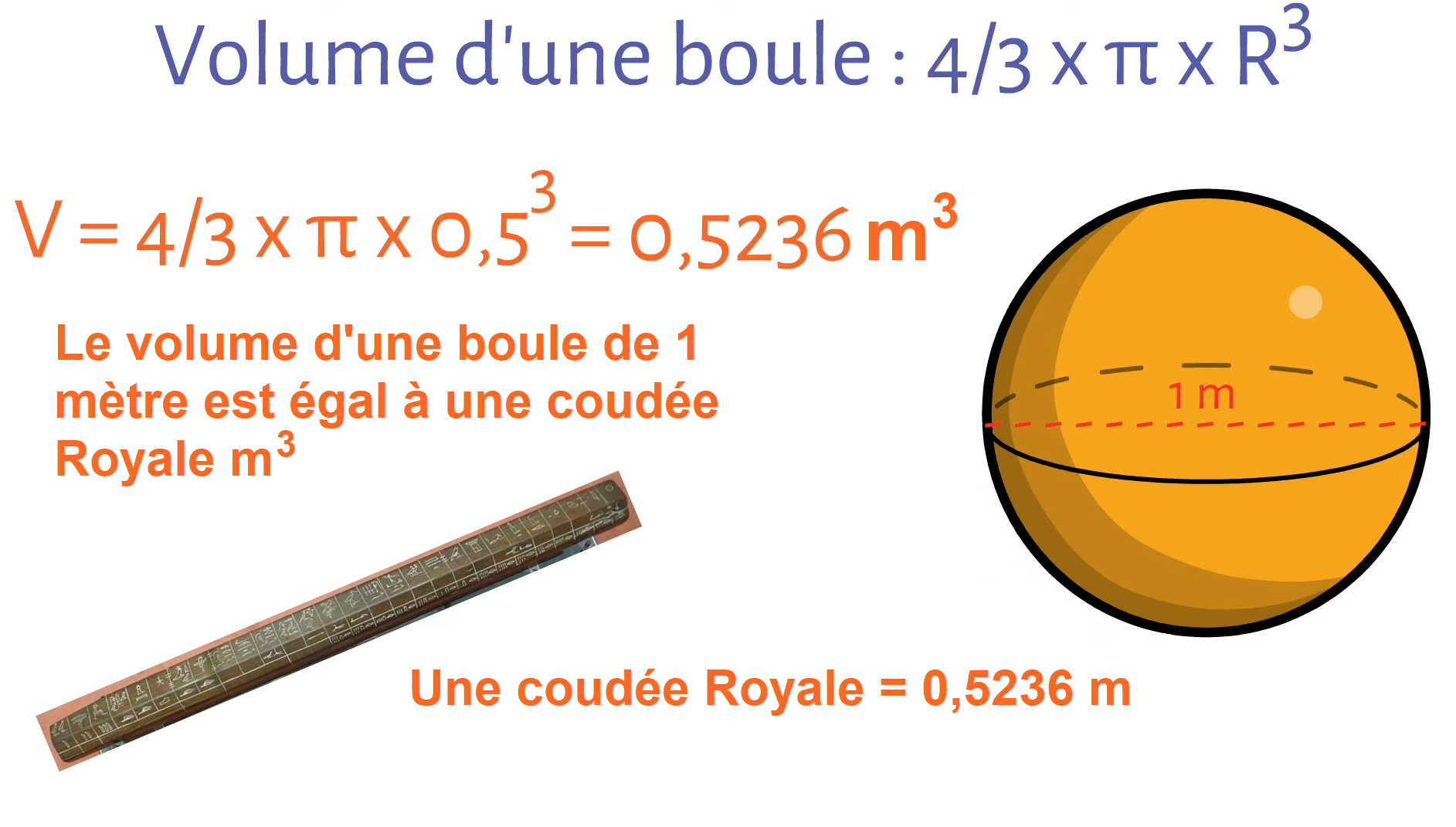
De même avec la coudée Royale qui est la mesure de référence des architectes égyptiens et qui est la longueur du bout du majeur du Pharaon jusqu’à son coude c’est à dire 52,36 cm.
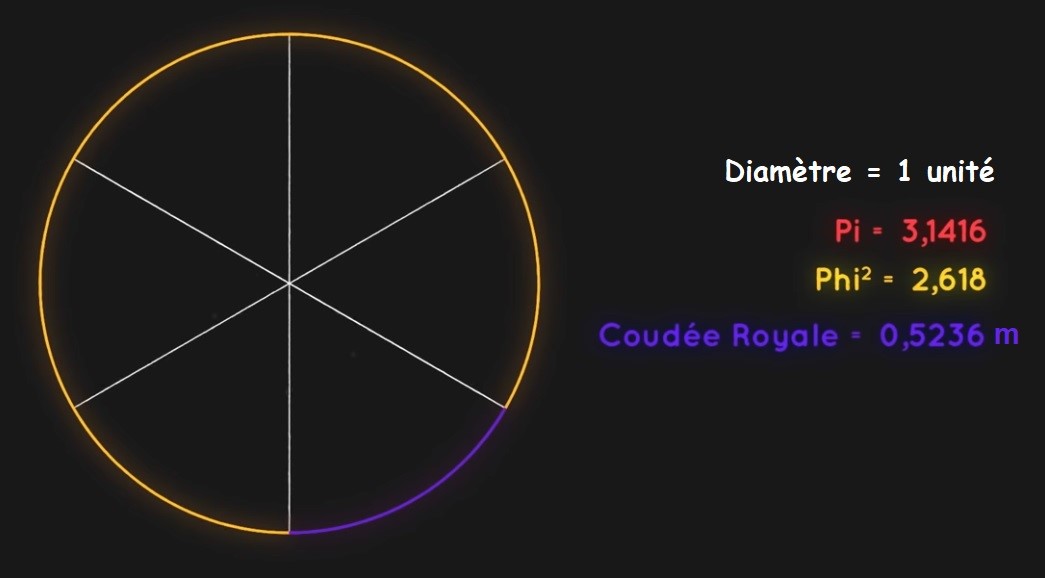
Hasard ou coïncidence, si on prend un cercle de 1 unité de diamètre alors son périmètre fera π .
La coudée royale sera le sixième de ce périmètre : \frac{\pi }{6} \approx 0,523598... \ unités
Il reste \frac{5\pi }{6} \approx 2,61799...\approx \varphi ^{2} \ unités
 |
 |
 |
 |
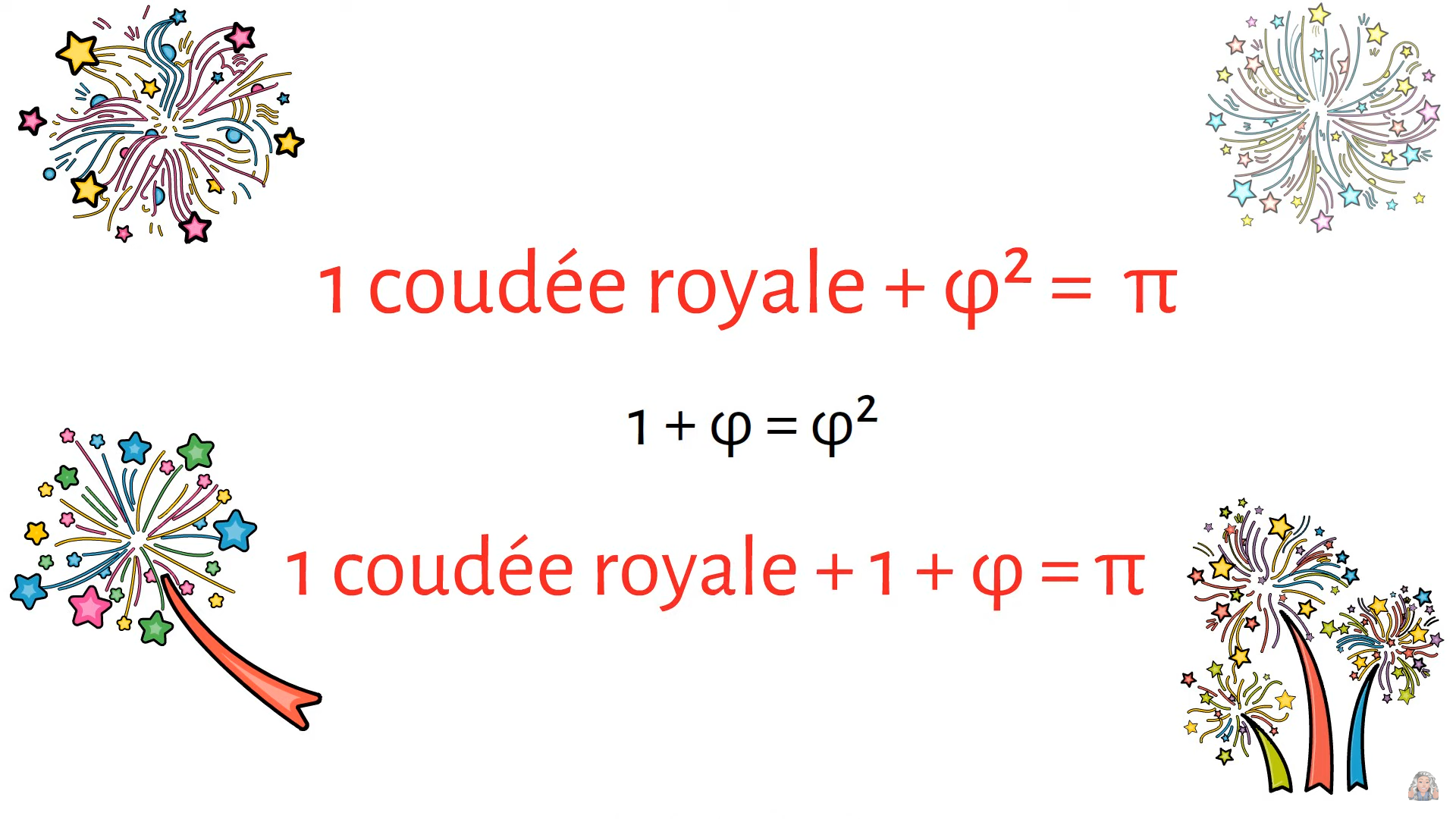 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
IX°/ Calcul de l’aire de n’importe quel polygone : Formule de Pick
I°/ Utilisation :
A°/ En comptant les points :
B°/ En comptant les côtés des quadrillages :
C°/ En comptant les carrés des quadrillages :
II°/ Démonstration :
A°/ Démonstration dans un rectangle :
B°/ Démonstration dans un triangle rectangle :
C°/ Démonstration dans un triangle quelconque :
D°/ Démonstration dans un polygone quelconque :
III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky
IV°/ Le théorème de Wallace-Bolyai-Gerwien :
V°/ La formule de Euler : S – A + F = 2
Le théorème de Pick permet de calculer l’aire de n’importe quel polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.
I°/ Utilisation :
Dessinons un polygone sur une feuille quadrillée. Si les sommets du polygone sont sur les nœuds du quadrillage et si ce polygone n’est pas croisé, alors on peut calculer très simplement son aire, c’est à dire la mesure de sa surface.
A°/ En comptant les points : Aire = e/2 + i – 1
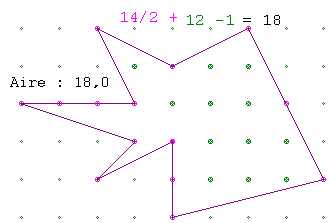 |
Soit e le nombre de points du réseau qui touchent les côtés, sommets compris (ici 14 points roses). Soit i le nombre de points qui sont à l’intérieur de la figure (ici 12 points verts). Aire = e/2 + i – 1 = 14/2 + 12 – 1 = 18 |
B°/ En comptant les côtés des quadrillages : Aire = i/2 + (c+t)/4
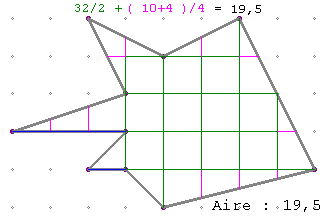 |
Soit i le nombre de côtés entièrement intérieurs à la figure (32 côtés verts). Soit c le nombre de côtés coupés intérieurs à la figure (10 côtés roses). Soit t le nombre de côtés de carrés sur la frontière de la figure (4 côtés bleus). Aire = i/2 + (c + t)/4= 32/2 + (10 + 4)/4 = 16 + 3,5 = 19,5 |
C°/ En comptant les carrés des quadrillages : Aire = e + c/2
 |
Soit e le nombre de mailles entièrement à l’intérieur de la figure (7 ronds verts). Soit c le nombre de mailles coupées par la frontière de la figure (11 ronds roses). Aire = e + c/2= 7 + 11/2 = 12,5 |
Entrainez-vous avec ce polygone :
Ou alors :
II°/ Démonstration :
Si : i = le nombre de points à l’intérieur du polygone.
b = le nombre de points sur les bords (côtés) du polygone.
Aire_{polygone}=i+ \frac{b}{2}-1
A°/ Démonstration dans un rectangle :
1°/ Par le calcul : Soit un rectangle ABCD de longueur AB et de largeur BC.
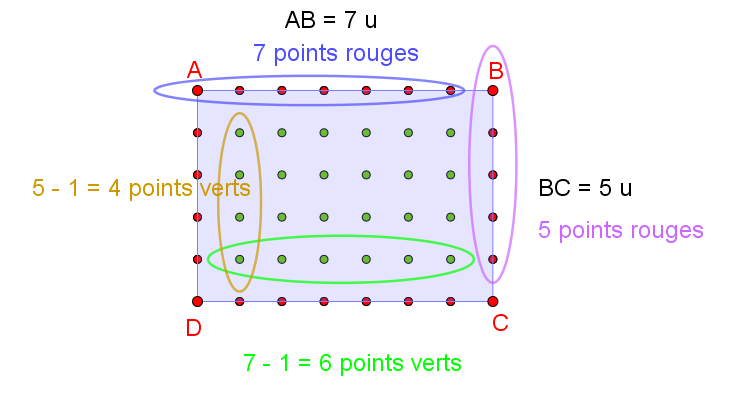 |
Points verts : i = (AB – 1)(BC – 1)
Points rouges : b = 2x(AB + BC) Donc : Aire_{polygone}=i+ \frac{b}{2}-1 = ABxBC – AB – BC + 1 + AB + BC – 1 = ABxBC Donc la formule de Pick nous donne bien la formule générale de l’aire d’un rectangle : Longueur fois largeur. Dans l’exemple : Aire_{rectangle}=i+\frac{b}{2}-1=24+\frac{24}{2}-1=24+12-1=35 u^{2} Aire_{rectangle}=L \times l =7 \times 5=35 u2 La formule de Pick est vérifiée pour les rectangles. |
2°/ Par la géométrie : Soit un rectangle ABCD de longueur AB et de largeur BC.
Décalons le quadrillage d’un demi carreau pour intégrer les points verts dans des carrés de même surface que les carrés représentés par 4 points de couleurs.
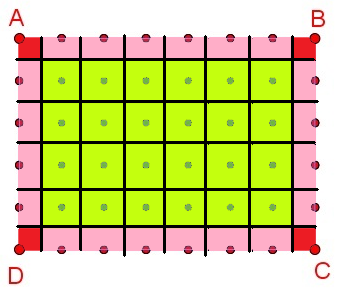 |
Nombre de carrés verts contenant les points verts : (AB – 1)(BC – 1) = ABxBC –AB – BC + 1
Nombre de rectangles roses contenant les points rouges : 2 x [(AB – 1) + (BC – 1)] = 2AB + 2BC – 4 Nombre de carrés rouges contenant les points rouges : 4 Donc : Points verts : i = (AB – 1)(BC – 1) = ABxBC –AB – BC + 1 Points rouges : b = 2AB + 2BC – 4 + 4 = 2AB + 2BC Aire_{rectangle}=i+ \frac{b}{2}-1 = ABxBC –AB – BC + 1 + AB + BC -1 = ABxBC = Longueur fois largeur. |
B°/ Démonstration dans un triangle rectangle :
Un triangle rectangle est la moitié d’un rectangle. Donc :
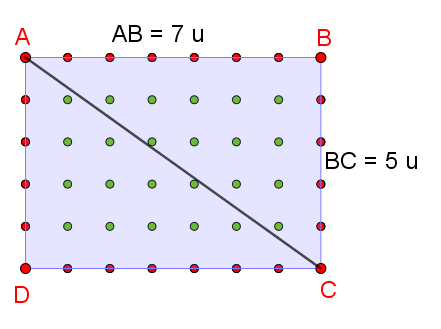 |
Points verts du triangle : it
Points rouges des côtés perpendiculaires du triangle : bt Points rouges de l’hypoténuse du triangle sans les extrémités : h Points verts du rectangle (ceux des 2 triangles plus ceux présents sur l’hypoténuse) : ir = 2 it + h Points rouges du rectangle (ceux des 2 triangles, sans les 2 hypoténuses, moins 2 sommets comptés 2 fois) : br = 2 bt – 2h – 2 Aire_{rectangle}=i+ \frac{b}{2}-1= 2 it + h + bt – h – 1 – 1 = 2it + bt – 2 = 2\times (i_{t}+\frac{b_{t}}{2} -1) Aire_{rectangle}=2 \times Aire_{triangle} |
C°/ Démonstration dans un triangle quelconque :
On peut inscrire un triangle quelconque dans un rectangle. t1 = AED ; t2 = EBF; t3 = FCD et t = CDE
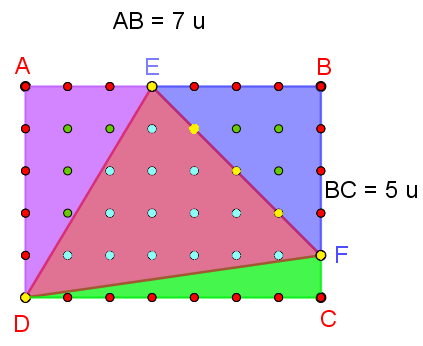 |
Points verts du rectangle ABCD (ceux des 4 triangles plus ceux présents sur les hypoténuses des 3 triangles rectangles) :
ir = it1 + h1 + it2 + h2 + it3 + h3 + it Points rouges du rectangle (ceux des 3 triangles t1, t2 et t3, sans leurs hypoténuses, moins 6 sommets comptés 2 fois pour chacun des 3 triangles) : br = bt1 – h1 + bt2 – h2 + bt3 – h3 – 6 De plus les points sur les bords du triangle CDE sont ceux présents sur les 3 hypoténuses : bt = h1 + h2 + h3 |
Aire_{CDE}=Aire_{ABCD}-Aire_{AED}-Aire_{EBF}-Aire_{FCD}
Aire_{CDE}=i_{R}+\frac{b_{r}}{2}-1-i_{T1}-\frac{b_{T1}}{2}+1-i_{T2}-\frac{b_{T2}}{2}+1-i_{T3}-\frac{b_{T3}}{2}+1
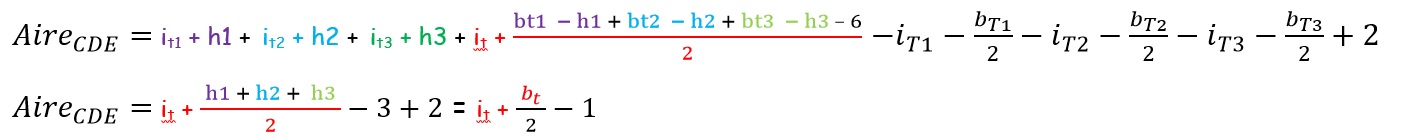
La formule de Pick est vérifiée pour les triangles quelconques.
Vérification sur l’exemple : Aire_{DEF}=i_{t}+ \frac{b_{t}}{2}-1 = 14 + \frac{6}{2}-1 = 16 unités d’aire
D°/ Démonstration dans un polygone quelconque :
Tout polygone peut être découpé en triangles, donc le théorème de Pick est à présent démontrer pour tout polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.
III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky
Ce théorème vaut par son titre amusant (à dire rapidement : mémère – pépère …), qui n’en est pas moins exact.
Il dit que si on peut découper un carré en triangles de même aires, alors il y a un nombre pair de triangle.
Autrement dit de façon Mathématiques mais mois rigolo, un carré n’admet pas d’équidissection impaire.
On peut généraliser ce théorème à tous les polygones.
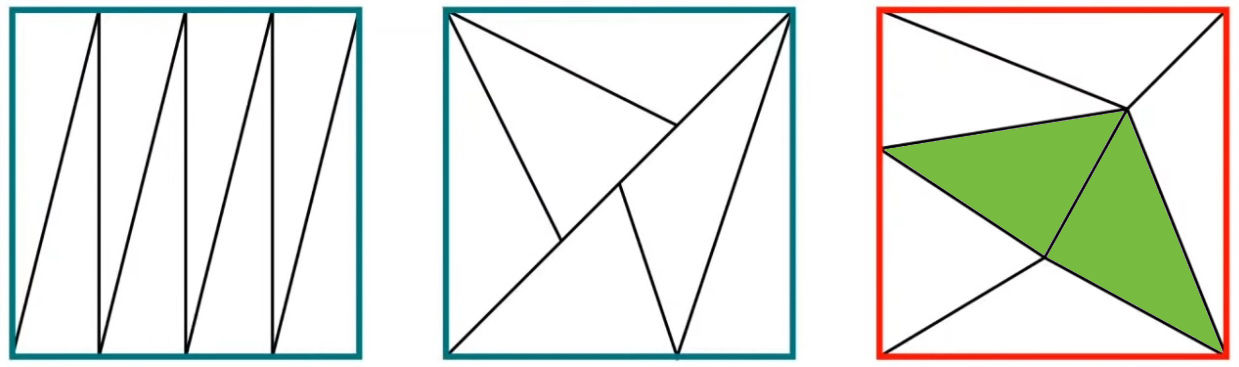
Il y a 8 triangles de même aire dans le premier carré et 6 de même aire dans le second. Par contre dans le troisième carré rouge, il y a 7 triangles dont les deux verts n’ont pas la même aire que les autres.
IV°/ Le théorème de Wallace-Bolyai-Gerwien : les formules des aires des polygones et des volumes des solides
Les matheux aiment le découpage : la preuve avec le théorème de Wallace-Bolyai-Gerwien et avec le théorème de Dehn !
Dans cette vidéo de El JJ nous verront comment retrouver les formules des aires des polygones et des volumes des solides par découpage, comment passer d’un polygone ou d’un polyèdre à un autre toujours par découpage et enfin nous découvrirons le 3ième problème de Hilbert.
V°/ La formule de Euler : S – A + F = 2
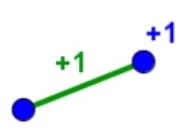
Pour les polygones, la formule d’Euler affirme que : S + R = A + 2 (S nombre de sommets, R nombre de régions délimitées par les arêtes et A nombre d’arêtes)
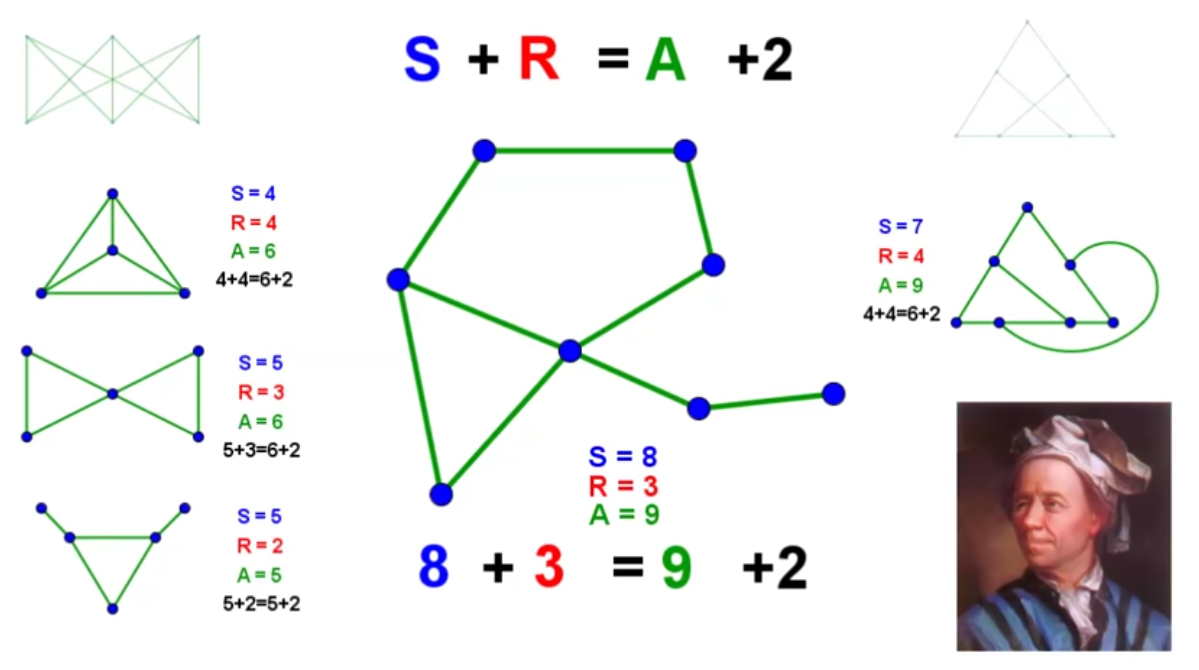
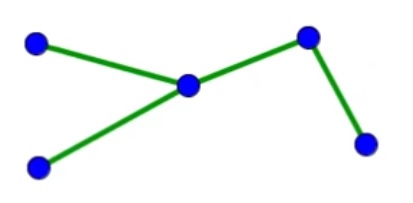
| 1 points | + 1 points = + 1 arêtes, donc pas de changement dans la formule. | + 1 région sans sommet = + 1 arête | ||
| Schéma | 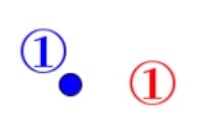 |
 |
 |
 |
| Sommet S | S = 1 | S + 1 = 1 + 1 = 2 | S + 4 = 5 | S = 5 |
| Régions R | R = 1 | R = 1 | R = 1 | R = 2 + 1 = 3 |
| Arêtes A | A = 0 | A + 1 = 0 + 1 = 1 | A + 4 | A = 5 + 1 = 6 |
| Formule d’Euler S + R = A + 2 |
1 + 1 = 0 + 2 = 2 | 2 + 1 = 1 + 2 = 3 S + 1 + R = A + 1 + 2 S + R = A + 2 |
5 + 1 = 4 + 2 = 6 S + 4 + R = A + 4 + 2 S + R = A + 2 |
5 + 3 = 6 + 2 = 8 S + R + 1 = A + 1 + 2 S + R = A + 2 |
Tour de magie :
Cette formule permet de créer un petit tour de magie assez bluffant : gribouiller n’importe comment. La seule chose qui importe, c’est que le gribouillage soit en un seul morceau (connexe). Par exemple, vous pouvez faire un truc comme ça :
 |
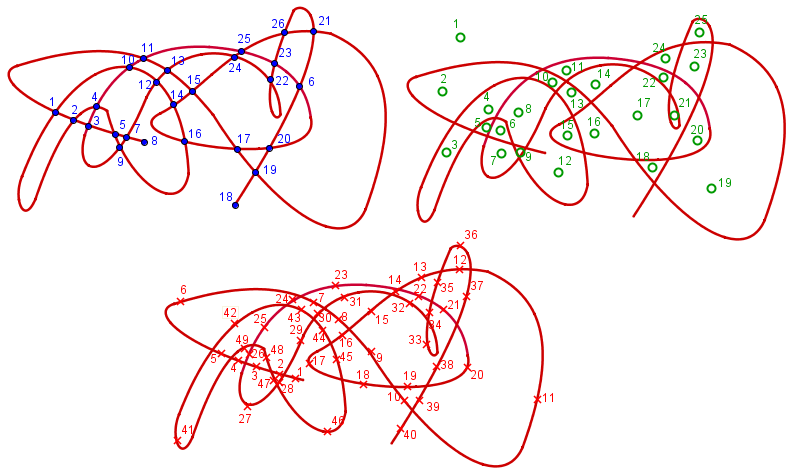 |
C’est maintenant qu’on va faire des maths ! Dans ce gribouillage, on peut repérer des « Sommets » S (les points d’intersection et les extrémités), des « Arrêtes » A (ce qui relie deux sommets) et des « Régions » R (les cellules, délimitées par des arrêtes. Au passage, l’extérieur de la figure est une face. On les appellent souvent Face F.). Comptez-les !
Moi, je compte S = 26 sommets (bleus), A = 49 arrêtes (rouges) et F = 25 faces (verts)
Attention, tour de magie qui n’impressionnera personne. Je suis sûr que si vous effectuez l’opération S – A + F = 26 – 49 + 25 = 2, vous trouverez toujours 2 !
La formule d’Euler pour les polyèdres convexes : S + F = A + 2 (S nombre de sommets, F nombre de faces et A nombre d’arêtes).

Une très belle vidéo :
| Vertices = sommets
Edges = arêtes Faces = faces Dans un polyèdre : Nombre de sommet – Nombre d’arêtes + Nombre de face = 2 S – A + F = 2 Ou en Anglais : V – E + F = 2 |
XIV°/ Le format A4 des feuilles :
L’idéal pour une feuille, serait que son format ne change pas lorsqu’on la plie en deux ou que l’on fait un agrandissement ou une réduction avec une photocopieuse.
Pour cela le rapport Longueur sur largeur doit être constant d’un format à l’autre, et pour que l’on puisse plier parfaitement une feuille en deux.
Quel doit être ce rapport ?
Dans le tableau excel suivant, on se rend compte que si on prend une Longueur 2 fois plus grande que la largeur, le format suivant est un carré de rapport 1, puis le suivant un rectangle de rapport 2 et ainsi de suite. Avec les images qui suivent où la Longueur de départ est le double de la largeur, le burro Catalan grossit puis revient aux bonnes proportions au fil des réductions.




Utilisez ce fichier Excel pour fabriquer vos propres formats : Format A4. http://trabucaire.free.fr/wp-content/uploads/2020/07/Racine-carree-compte-goutte.xlsx
Format B4 où le rapport L/l n’est constant.
Pour que les images ne se déforment pas, quel doit être le bon rapport ?
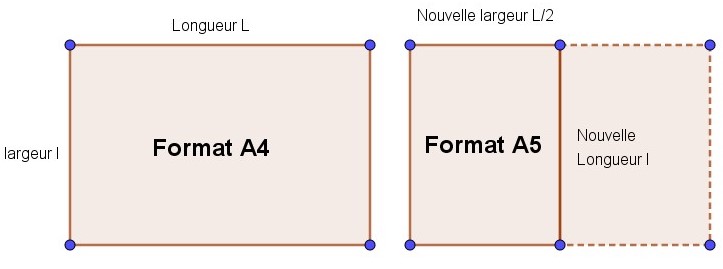 |
Soit L la longueur d’une feuille et l sa largeur.
Lorsqu’on la coupe en deux, la largeur de la nouvelle feuille est la moitié de la Longueur précédente, et sa longueur est maintenant l. Pour avoir la même forme il faut que le rapport des deux mesures soit identique : \frac{Ancienne \ Longueur \ L}{Ancienne \ largeur \ l} = \frac{Nouvelle\ Longueur \ l}{Nouvelle\ largeur \ L/2} \Rightarrow \frac{L^{2}}{l^{2}}=2 \Rightarrow \frac{L}{l} = \sqrt{2}\approx 1,414 |
La première référence au rapport \sqrt{2} ce trouve dans une lettre écrite le 25 octobre 1786 par le professeur de physique Georg Christoph Lichtenberg (Université de Göttingen, Allemagne, 1742-1799) à Johann Beckmann. Il se trouve que le papier sur lequel était écrit cette lettre respecté justement ce rapport de \sqrt{2} entre la Longueur et la largeur.
L’Organisation Internationale de Normalisation (ISO) constitua en 1947 le Comité Technique ISO/TC 6 « papier » qui chargea un de ses sous-comités d’étudier les dimensions internationales des papiers et des cartons. La recommandation fut demandée d’envisager la normalisation des formats.
Comme nous l’avons vu ci-dessus, lorsqu’on plie en deux une feuille A4, le format reste identique : le rapport longueur sur largeur de la feuille reste constant. C’est très pratique. Ainsi nous passons du format A3 au format A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant également en deux une feuille A4.
Le format de départ A0 est défini comme ayant une surface mesurant 1 m². Quelles seront ces dimensions ?
| Format | Longueur en cm | largeur en cm | Rapport | Aire en m² | Poids en g |
| A0 | 118,9 | 84,1 | \frac{118,9}{84,1} =1,413794 | 1 | 80 |
| A1 | 84,1 | 59,5 | \frac{84,1}{59,5} =1,413445 | 1/2 | 40 |
| A2 | 59,5 | 42 | \frac{59,5}{42} =1,416667 | 1/4 | 20 |
| A3 | 42 | 29,7 | \frac{42}{29,7} =1,414141 | 1/8 | 10 |
| A4 | 29,7 | 21 | \frac{29,7}{21} =1,414286 | 1/16 | 5 |
| A5 | 21 | 14,8 | \frac{21}{14,8} =1,418919 | 1/32 | 2,5 |
Ainsi le rapport Longueur/Largeur est identique pour toutes les feuilles et chacune contient exactement deux feuilles du format immédiatement inférieur.
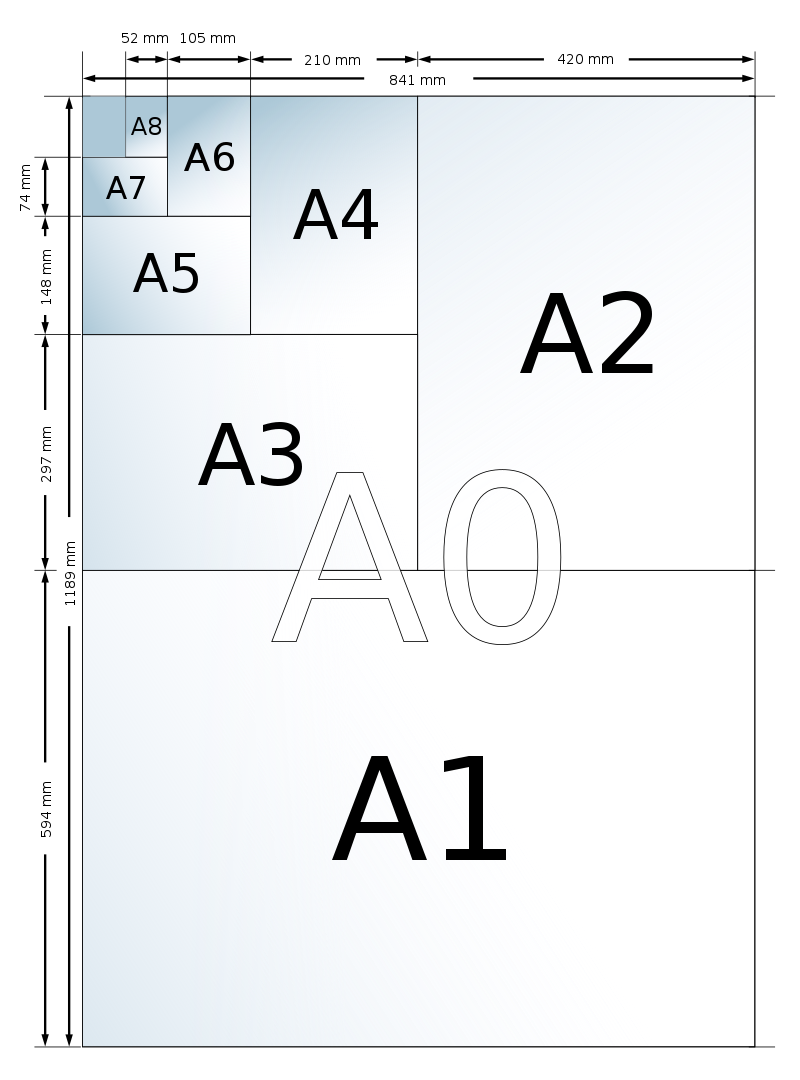
Notons qu’avec du papier 80g/m², une feuille A4 d’aire 1/16 m² pèse 5g. Nous pouvons donc placer 3 feuilles dans une enveloppe et mettre un timbre normal sur l’enveloppe (moins de 20g).
XV°/ La casserole :
Les Mathématiques sont utiles en tout, notamment pour faire des économies.
Prenons le cas des casseroles. Pour un volume égal, quel doit être le rapport entre la hauteur et le rayon, en sachant que plus la surface sera petite et moins il faudra de métal pour la construire. Donc un fabriquant de casserole pourrait se demander si, pour un volume égal, la forme de la casserole influe sur son prix. A première vue, qu’elle soit plus large ou plus haute ne change pas la quantité de métal nécessaire et donc son prix. Et bien ….
Soit : R = Rayon et h = hauteur :

Conclusion, il faut que le rayon R de la casserole soit égal à sa hauteur.
Voici un fichier Excel pour voir : La casserole.(Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)
En faisant varier le volume de la casserole dans le fichier Excel, on se rend bien compte le rapport V/S (cad Volume sur Surface, la courbe bleue) est maximal lorsque la différence R-h (cad Rayon moins hauteur, la courbe rouge) est lui minimal, autrement dit que le hauteur de la casserole se rapproche du Rayon.
XV°/ Les preuves par 9 et par 11 :
a/ La preuve par 9 :
Cette preuve qui est encore utilisée à bon escient dans certaines classes.
Tout de même cette preuve n’en a que le nom, car si elle est fausse c’est certain, notre opération est fausse. Mais si elle tombe juste alors l’opération est peut-être bonne… cependant ce n’est pas sûr, car 2 erreurs peuvent s’annuler.
Toutefois elle est intéressante car elle fait réfléchir sur la technique de l’opération.
Habituellement elle est utilisée pour la multiplication et la division, mais elle peut être également utilisée pour l’addition et la soustraction.
Elle repose sur le principe suivant : on refait l’opération désirée en remplaçant chacun des nombres par son reste dans la division par 9.
Ce reste sera un nombre de 0 à 8.
On sait que ce reste est le même que celui de la somme des chiffres du nombre. Chaque fois qu’il y a un 9, on peut le remplacer par 0.
On recommence le procédé jusqu’à ce qu’on obtienne un nombre plus petit que 9.
Ainsi pour le nombre 7 854 672 on obtiendra d’abord 7 + 8 + 5 + 4 + 6 + 7 + 2 soit 39 qui va donner 3.
3 est le reste de 7 854 672 dans la division par 9. Vous pouvez le vérifier.
Si on le désire on peut remplacer chaque somme partielle comme 7 + 8 = 15 par 1 + 5 = 6 et ainsi de suite…
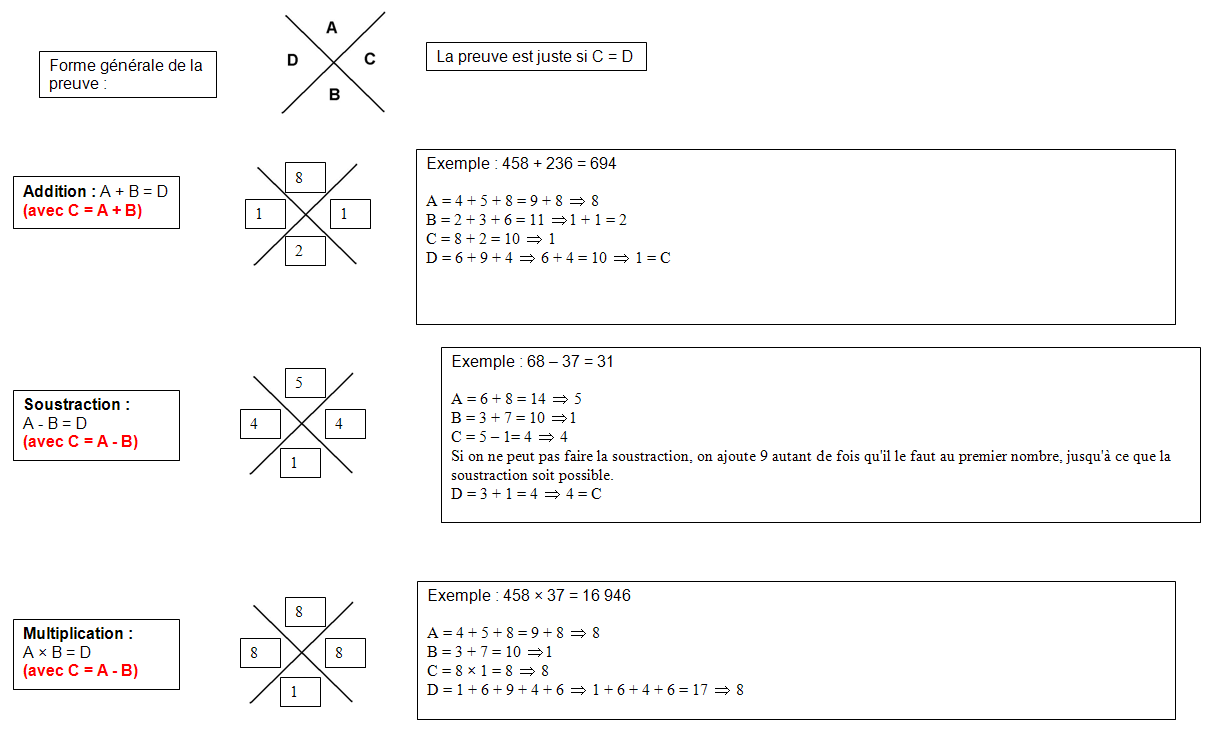

Voici un fichier Excel pour vous entrainer : La preuve par 9. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)
b/ La preuve par 11 :
Le principe est le même que celui de la preuve par 9, mais on utilise cette fois le critère de divisibilité par 11.
Comme il fait appel à une soustraction, il n’est pas enseigné à l’école primaire parce qu’on peut tomber sur un nombre négatif avec la soustraction.
On sait que ce reste est le même que celui de la somme des chiffres de rang impair en partant de la droite moins la somme des chiffres de rang pair en partant de la droite.
C’est un peu compliqué à dire mais facile à mettre en œuvre voici un exemple :
Ainsi pour le nombre 79 859 632 on fera : (2 + 6 + 5 + 9) – (3 + 9 + 8 + 7) = 22 – 27
Nous sommes dans le cas où 27 est plus grand que 22. Alors on ajoute à 22 autant de fois de 11 qu’il le faut, pour obtenir une soustraction avec un résultat positif : 22 + 11 = 33
Et le nombre a même reste que 33 – 27 soit 6.
On recommence jusqu’à obtenir un nombre plus petit que 11.


Voici un fichier Excel pour vous entrainer : La preuve par 11. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)
VIII°/ Les nombres premiers :
Un nombre est dit premier, s’il admet exactement 2 diviseurs distincts (lui-même et l’unité). 1 n’est donc pas premier.
A°/ Crible d’Ératosthène :
B°/ Crible géométrique :
C°/ Les nombres premiers particuliers :
D°/ Visualisation des nombres premiers :
A°/ Crible d’Ératosthène :
On désigne sous le nom de crible d’Ératosthène une méthode de recherche des nombres premiers plus petits qu’un entier naturel n donné.
Pour ceci, on écrit la liste de tous les nombres jusqu’à n.
– On élimine 1.
– On souligne 2 et on élimine tous les multiples de 2.
– Puis on fait de même avec 3.
– On choisit alors le plus petit nombre non souligné et non éliminé ici 5, et on élimine tous ses multiples.
– On réitère le procédé jusqu’à la partie entière de la racine de n.
Les nombres non éliminés sont les nombres premiers jusqu’à n.
Les nombres premiers plus petits que 100 sont donc :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Les nombres premiers sont connus depuis l’Antiquité mais en dépit de la fascination qu’ils exercent il n’a pas encore été possible de percer leur mystère, c’est-à-dire de savoir s’il existe ou non, une loi de leur formation.
Euclide démontrait très simplement dans les Eléments (livre IX, 20) que la suite des nombres premiers était illimitée, et donc leur nombre infini.
En 1971, Tuckermann calcula un nombre premier avec 6 002 chiffres : 219937 – 1.
Le plus long nombre premier, comptant plus de 7 millions de chiffres, a été découvert grâce au programme du GIMPS (Great Internet Mersenne Prime Search) qui utilise des ordinateurs en réseau pour effectuer les monstrueux calculs nécessaires à la découverte de tels objets mathématiques
B°/ Crible géométrique :
Ci-dessous une parabole et son axe de symétrie horizontal.
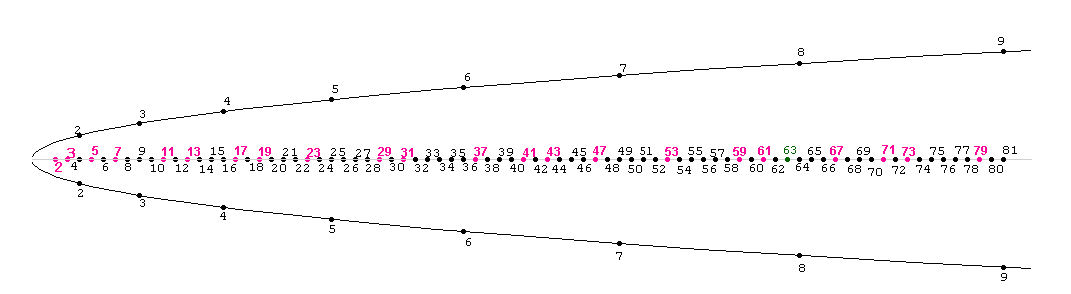
Le produit de deux nombres entiers notés sur chaque branche de la courbe, se lit directement à l’intersection du segment vert et de l’axe de la parabole (la ligne droite médiane qui est l’axe de symétrie de la parabole).
En plaçant des points de coordonnées entières sur chaque branche de la parabole et en les reliant systématiquement par des segments coupant l’axe de symétrie, on obtient les produits de ces deux entiers.
Les points (à abscisse entière) de l’axe par lesquels les segments ne passent pas sont donc des nombres premiers (2).
Ainsi nous obtenons un crible géométrique très simple pour trouver les nombres premiers.
Cette idée simple et géniale nous vient des mathématiciens russes Yuri Matiiassevitch et Boris Stechkin.
Cliquez sur crible géométrique.fig pour voie l’animation :
C°/ Les nombres premiers particuliers :
1/ Un nombre premier particulier : 2357223335555577777772357
Il est composé de 2357 puis de deux 2, puis de trois 3, puis de cinq 5, puis de sept 7 et enfin il finit de nouveau par 2357.
2/ Nombres premiers jumeaux : ils sont séparés par 2 unités. Les trois plus petits couples de nombres premiers jumeaux sont (3, 5), (5, 7) et (11, 13).
Le plus grand connu est 2 996 863 034 895 × 221 290 000 ± 1. Les deux nombres possèdent 388 342 chiffres (septembre 2016).
On soupçonne qu’il existe une infinité de ces couples, mais personne n’a pu le prouver à ce jour.
3/ Nombres premiers cousins : ils sont séparés par 4 unités.
4/ Nombres premiers sexys : ils sont séparés par 6 unités.
5/ Nombres premiers de Pythagore : Les nombres premiers de la forme 4n + 1, où n est un entier naturel. Par exemple, le nombre premier 5 est de Pythagore.
6/ Nombres premiers de Mersenne: Les nombres premiers de la forme Mp = 2p – 1 où p est alors nécessairement aussi premier.
7/ Nombres premiers de Fermat : Les nombres premiers de la forme Fn = 22n où n est un entier naturel. Petit soucis de définition, seuls les 5 premiers nombres de Fermat sont premiers ….
6/ Nombres premiers de Sophie Germain : Un nombre premier G est un nombre premier de Sophie Germain si 2G + 1 est aussi un nombre premier, appelé nombre premier sûr. Les dix premiers nombres premiers de Sophie Germain sont 2, 3, 5, 11, 23, 29, 41, 53, 83, 89.
8/ Nombres premiers rep-units : S’écrit seulement avec des 1. Par exemple, 1, 11 que l’on notera (1)2.
Jusqu’à présent, on ne connait que 5 repunits premiers : 11, (1)19, (1)23, (1)317 (Williams – 1978) et (1)1031. (Williams et Dubner – 1985). Pour tous les autres n inférieurs à 30 000, il n’y a pas de repunits premiers. Après, les calculs deviennent un brin compliqués…
Les repunits probablement premiers sont (1)49 081 (Dubner – 1999), (1)86 453 (Baxter – 2000), (1)109 297 (Dubner – 2007) et (1)270 343 (Voznyy – 2007). Et on s’arrête là, c’est déjà pas mal !
9/ Nombres premiers palindromes : Qui se lisent dans les deux sens.
Nombre à 1 seul chiffre : 2, 3, 5, 7.
En considérant que 1 est un nombre premier :
Nombre à 2 seul chiffres : il n’y a que 11, les autres seront des multiples de 11.
Nombre à 3 seul chiffres : 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929.
Nombre à 4 seul chiffres : il n’y a pas un seul nombre premier palindrome !
Nombre à 5 seul chiffres : il y en a 93.
En fait, on peut facilement voir que tout nombre palindrome de longueur paire est divisible par 11, car il vérifie le critère de divisibilité par 11 !
Pour les curiosités des nombres premiers palindromes, on a :
* 1 023 456 987 896 543 201, le plus petit palindrome premier qui contient tous les chiffres de 0 à 9
* 1(0)749997426247(0)749991, ((0)74999, c’est une suite de 74999 zéros) est le plus grand palindrome premier prouvé comme tel ! (Joblin – 2005 – 150 007 décimales)
* 1(0)56514661664(0)56511 est un nombre premier triplement palindrome : il est premier, il est palindrome, et son nombre de chiffres, 11311, est également palindrome et premier !
10/ Les nombres premiers raccourcissables : Le nombre 35 768 631 264 6216 567 629 137 est le plus long nombre premier connu qui reste premier si on lui enlève son premier chiffre. Un nombre premier de ce type est appelé « raccourcissable à gauche ». 73939133 et 1979339333 sont « raccourcissable à droite et 11311, 71317, 93739, 1335331, 3315133 et 9375739 sont « raccourcissable à gauche » et à droite !!!
11/ Méchant Premier :
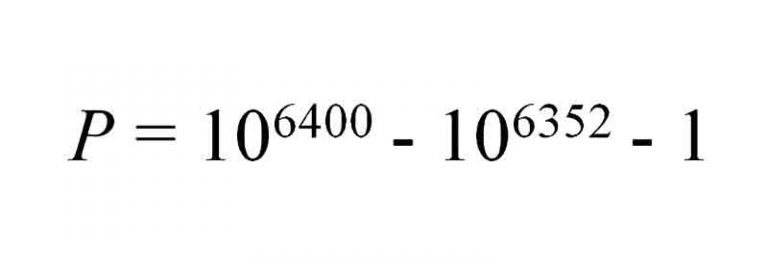
Le nombre premier P contient 6400 chiffres composés de 9 à l’exception d’un seul 8 caché dans le paquet de chiffres :
999999999999999999999999999999999999999999999999999899999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999
12/ Le plus grand :
\Large 2^{136279841}-1Découvert le 12 octobre 2024, c’est le plus grand nombre premier connu. Ce nombre a 41 024 320 chiffres… C’est (comme toujours) un nombre premier de Mersenne.
Il a fallu près de 6 ans au logiciel GIMPS pour le trouver après le précédent record.
D°/ Visualisation des nombres premiers :
|
Chaque nombre est décomposé en ses multiples, par exemple : 12 = 3 x 4 boules. Les nombres premiers sont eux représentés sous forme de cercle. |
Mais on peut trouver d’autre façon de ranger les nombres premiers.
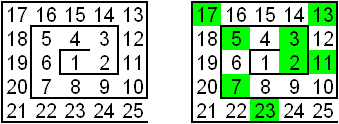 |
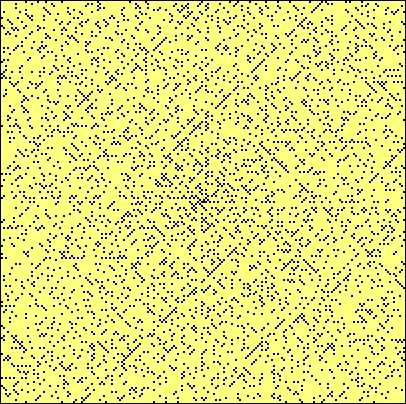 |
 |
| L’anecdote raconte qu’en 1963, le mathématicien Stanislaw Marcin Ulam fut contraint d’écouter un exposé très long et très ennuyeux. Il commença alors à écrire les entiers sous forme d’une spirale. Il entoura ensuite les nombres premiers… | Au premier abord, il n’y a rien à voir, mais si on pousse le dessin plus loin, on trouve cette spirale d’Ulam (ou « horloge d’Ulam ») (200×200) | Et si, au lieu de prendre une spirale carrée, on prend une vraie spirale ? Une spirale d’Archimède, par exemple. En s’arrangeant pour que tous les carrés parfait soient alignés, et en mettant le 0 au milieu, on trouve la spirale de Sacks (1994) |
XIV°/ Les sondages :
Comment les mathématiques déjouent le mensonge.
Il est des questions qui sont assez indiscrètes et embarrassantes et certaines personnes déforment leurs réponses. Ainsi si l’on demande à quelqu’un s’il lui arrive de commettre de petits délits il est difficile d’obtenir une réponse positive sachant que c’est puni par la loi.
Aussi les sondeurs peuvent-ils utiliser un procédé astucieux et mathématique qui demande seulement d’augmenter la taille de l’échantillonnage.
Dans l’exemple, la taille de l’échantillon est multipliée par 3. Si on veut 500 réponses il nous faudra 1500 personnes.
L’enquêteur dispose d’un sac contenant trois cartes qui seront tirées au sort par le sondé. Sur chacune des cartes une question est écrite où la réponse ne sera que oui ou non.
1- Sur la première carte Alpha est écrite la question qui intéresse le sondeur.
2- Sur une deuxième carte Béta est dessiné un disque noir et la question est : y-a-t-il un disque noir sur la carte ?
3- Sur la troisième carte Gamma rien n’est dessiné, il y a juste la question : y-a-t-il un disque noir sur la carte ?
L’enquêteur ignore bien entendu quelle carte est tirée. La personne interrogée sait cela et elle peut donc répondre honnêtement et sans aucun risque donner sa réponse car elle est la seule à connaître la question à laquelle elle répond.
Comment interpréter les réponses ?
Imaginons que l’enquêteur questionne 1500 personnes ( 3 fois se dont il a besoin). Supposons en outre que nous ayons à la fin du sondage 792 réponses affirmatives.
En moyenne le tirage au sort fait que 500 personnes ont tiré la première carte, 500 la deuxième et 500 la troisième (plus le panel est grand et moins l’erreur le serat). Sur les 792 réponses affirmatives 500 proviennent de la deuxième carte et il reste donc 292 réponses positives venant de la première carte Alpha.
Finalement on peut raisonnablement estimer que 292 personnes sur 500 ont répondu positivement à la question désirée.
Bien entendu la taille et le choix des échantillonnages sont fondamentaux pour obtenir de bonnes statistiques.








































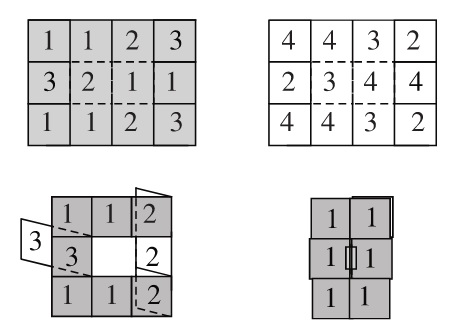
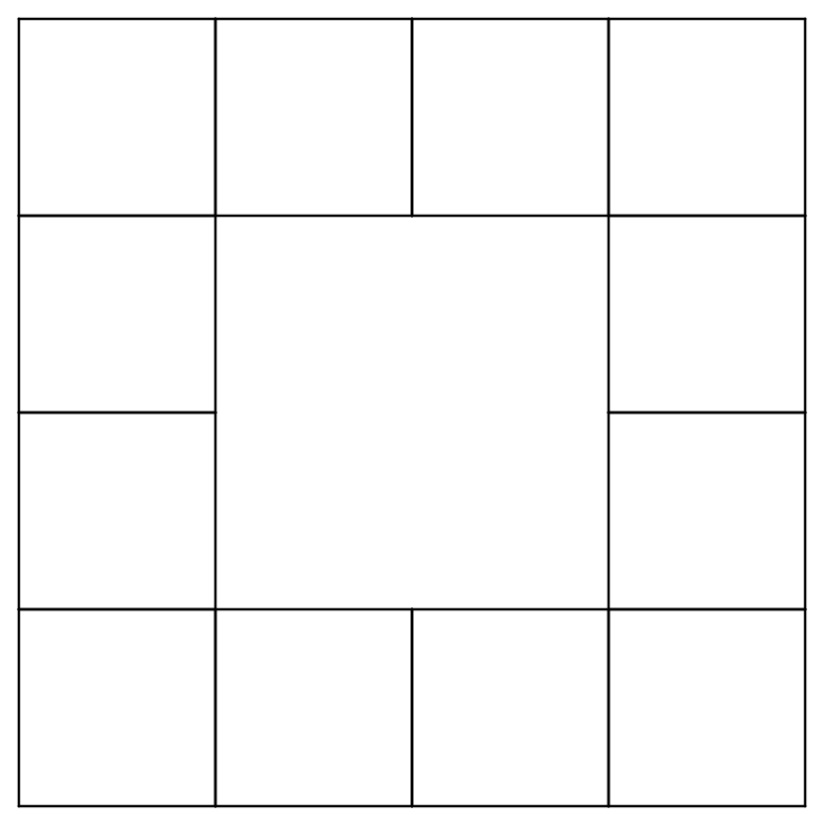 Le patron de l’hexatétraflexagone.
Le patron de l’hexatétraflexagone.