De tout temps les hommes ont cherché à protéger leurs messages des yeux indiscrets. Pour cela ils ont redoublé d’imagination pour chiffrer leurs messages.
I°/ Programme SCRATCH :
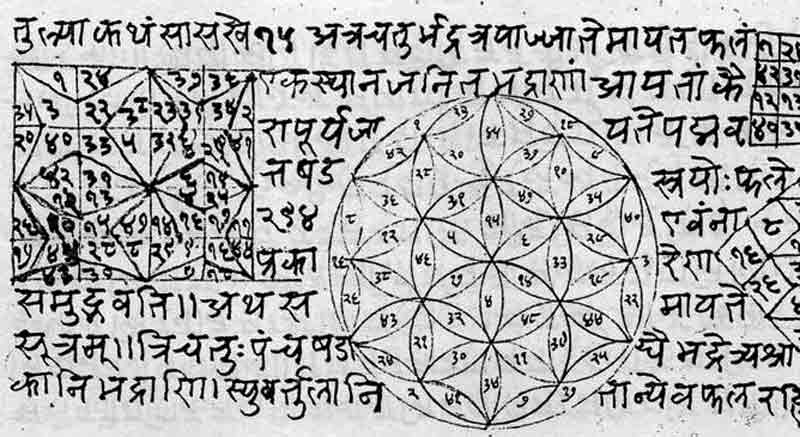
II°/ Historique :
III°/ Écriture Betamaze :
IV°/ Quadrillage carré :
V°/ Code alphabétique de Conway :
VI°/ Code de César affine :
VII/ Les grilles tournantes du colonel Fleissner :
I°/ Programme SCRATCH :
 |
Voici un programme Scratch pour s’amuser à coder et décoder. |
Exemple : codons Le petit Poucet (le mot de passe est entre les parenthèses).
| Texte clair | L | E | P | E | T | I | T | P | O | U | C | E | T |
| César (5) | Q | J | U | J | Y | N | Y | U | T | Z | H | J | Y |
| Atbash | O | V | K | V | G | R | G | K | L | F | X | V | G |
| Alphabet désordoné | I | Y | G | Y | N | C | N | G | D | R | E | Y | N |
| Mot-clef (mathweb) | I | W | N | W | R | D | R | N | L | S | T | W | R |
| Quadrillage | L | T | O | T | E | I | U | P | T | C | E | P | E |
| Code d’Alberti | L | F | R | H | X | N | Z | W | W | D | M | P | F |
| Vigenere (mathadore) | X | E | I | L | T | L | H | G | S | G | C | X | A |
| César affine (35) | O | T | A | T | M | F | M | A | X | P | N | T | M |
| Symétrie (stpaul) | Q | K | X | K | Y | G | Y | X | B | R | N | K | Y |
II°/ Historique :
Voici un florilège des méthodes de chiffrement les plus connues.
| Codage | Date | Méthode | Avantages | Inconvénients | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Antiquité | Antiquité | – Xerxès veut envahir la Grèce, il rase la tête d’un esclave, écrit le message sur le crâne et laisse repousser les cheveux. – Avaler le message écrit sur un tissu en soie enrobé de cire. – Écrire le message sur le bois d’une tablette de cire, puis la recouvrir de cire. |
Le message est caché et les moyens sont simples et nombreux. | Le message est en clair. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
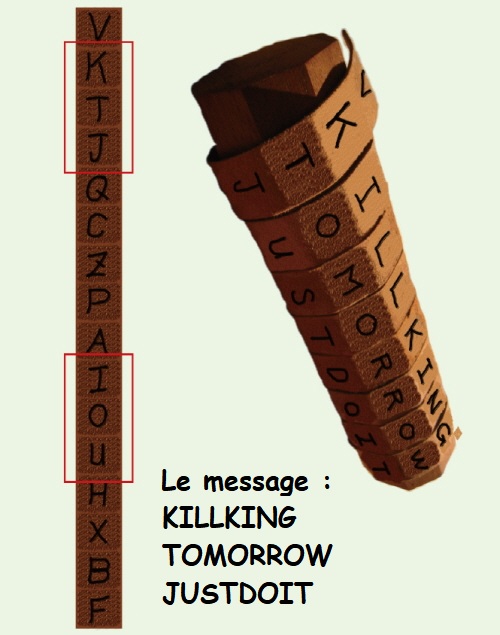
| La scytale spartiate | Vième Avt JC |
|
Une fois la lanière déroulée le message est illisible et elle peut servir de ceinture et être ainsi complètement anodine. | La protection n’est pas bien grande si on connait le procédé. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le chiffre Atbash | Les hébreux dès 500 av. JC | Il consiste simplement à écrire l’alphabet en sens contraire.
LEPETITPOUCET = OVKVGRGKLFXVG |
Le message est crypté et peu de gens savent lire. | Une fois la méthode connue, le message est clair. Or, certaines lettres sont plus fréquentes que d’autres dans une langue, donc une simple analyse fréquentielle permet de casser le code. En Français le E est très présent, donc la lettre la plus fréquente du message est certainement le E. Par exemple au Scrabble, certaines lettres valent plus de points que d’autres. Le Z vaut 10 points en France mais seulement 3 en Allemagne. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le code de César | Entre Ier et IX IXème siècle. Et même par l’armée Russe en 1915 |
Les lettres sont simplement décalées d’un nombre donné. Ici le 5.
LEPETITPOUCET = QJUJYNYUTZHJY |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Un mot-clef | Prenons un mot-clé facile à retenir, mettons MATHWEB, et de compléter ensuite le tableau par ordre alphabétique. Ceci donne ici :
LEPETITPOUCET = IWNWRDRNLSTWR |
Seul le destinataire connait le
mot-clef. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Poly-alphabétique : le code d’Alberti | 1404-1472 Alberti & Abbé Jean Triqueme | Il faut créer une grille. L’alphabet sur la 1ière ligne, puis on décale d’une lettre par ligne. Le message à coder est sur la colonne rouge et on repère sa correspondance sur la ligne bleue. Ainsi, le (L ; L) = L et le (E ; E) = F
LEPETITPOUCET = LFRHXNZWWDMPF |
La même lettre peut être codée par différentes lettres et inversement une lettre du message peut avoir plusieurs significations. | Si on connait la méthode, cela devient un jeu d’enfant. Le plus gros inconvénient c’est que l’abbé Triqueme a publié un livre sur sa méthode !!! |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Poly-alphabétique avec une clef : le code de Vigenere | Blaise de Vigenere 1523-1596 pendant 400 ans | Même chose que le code d’Alberti mais avec une clef.
C’est le couple lettre-clef et lettre-message qui code pour la lettre-code.
LEPETITPOUCET = XEILTLHGSGCXA |
C’est la même chose que le code d’Alberti mais avec une clef. L’ analyse fréquentielle ne sert plus à rien car la même lettre peut être codée par différentes lettres et inversement une lettre du message peut avoir plusieurs significations. | Charles Babage (1805-1881) casse le code de Vigenere. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Machine Enigma | 1945 | 1016 combinaison possibles. | Code cassé par Alan turing. Le principal inconvénient était qu’une lettre ne pouvait pas être codée par elle-même. |
Un site consacré au chiffrement. Gigantesque avec des outils automatiques : https://www.apprendre-en-ligne.net/crypto/index.html et sa section historique.
III°/ Écriture Betamaze :
Il existe beaucoup de façon de coder un message et certaines sont jolies et ludiques à défaut d’être performantes.
On peut par exemple utiliser la police d’écriture Betamaze, qui est très originale. On peut l’installer sur son ordinateur et l’utiliser dans Word par exemple (Télécharger la police).

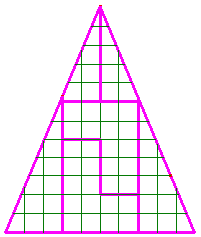
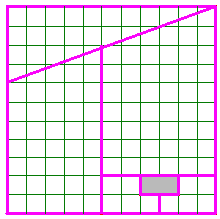
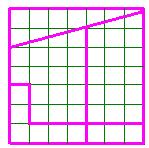
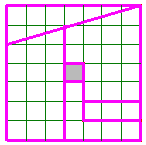
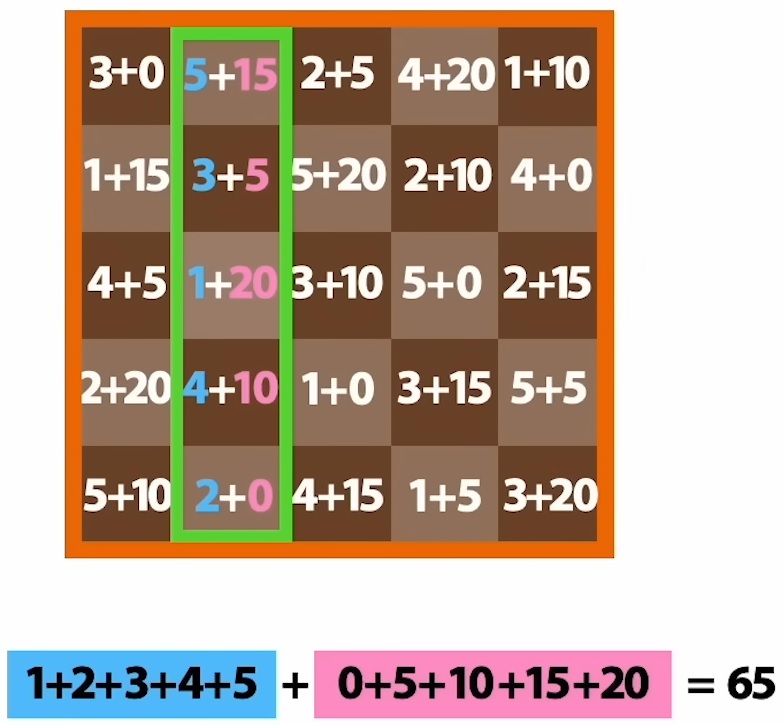
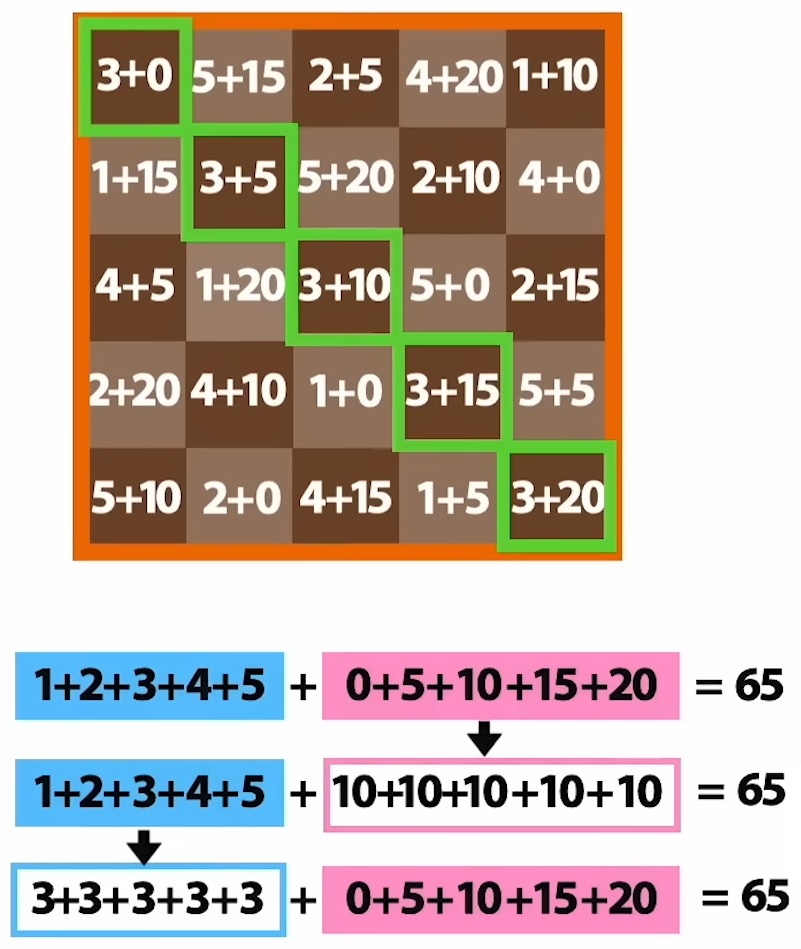
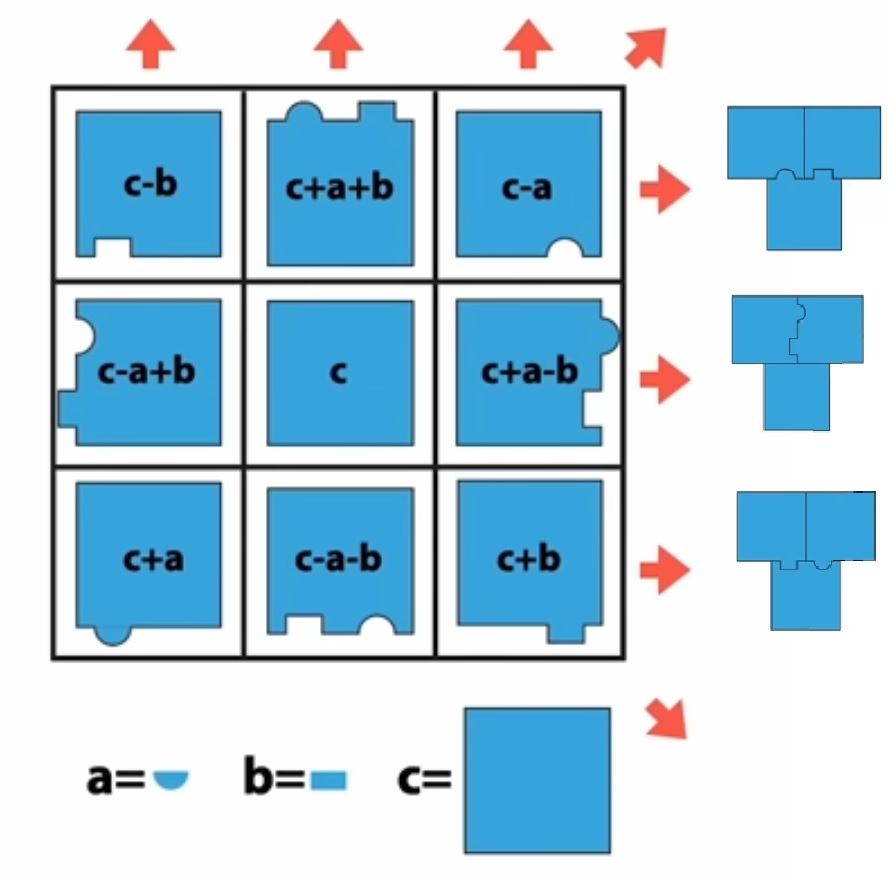
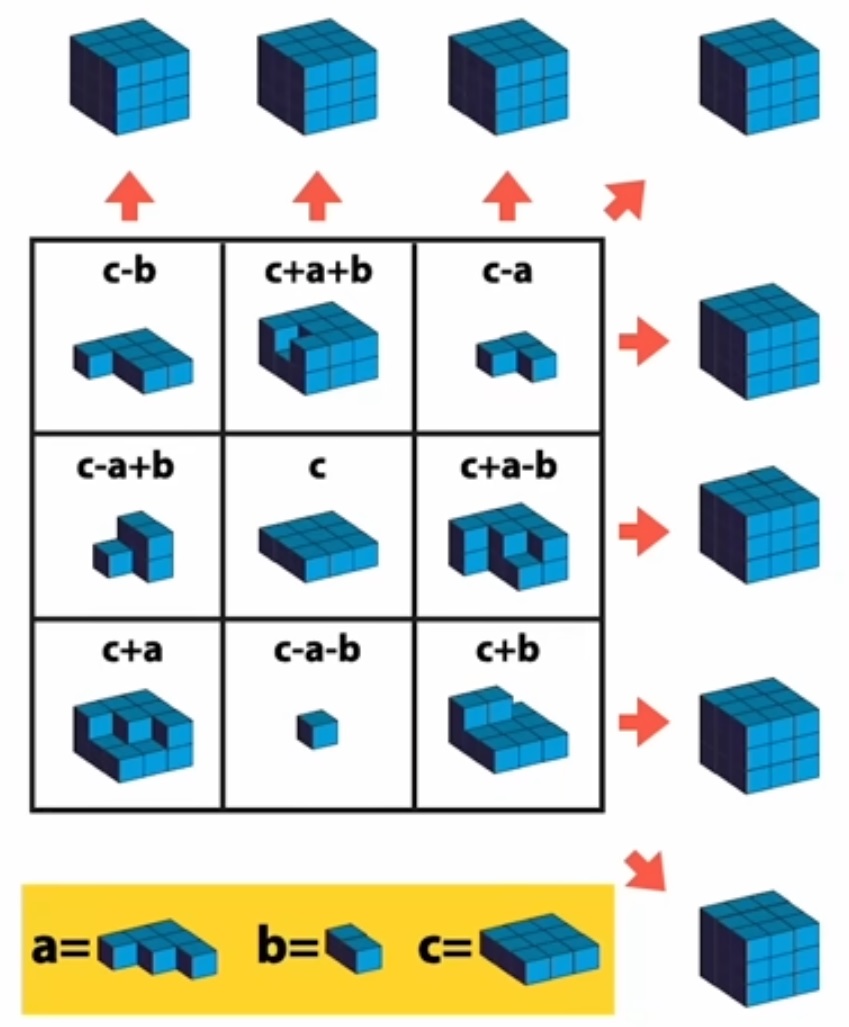
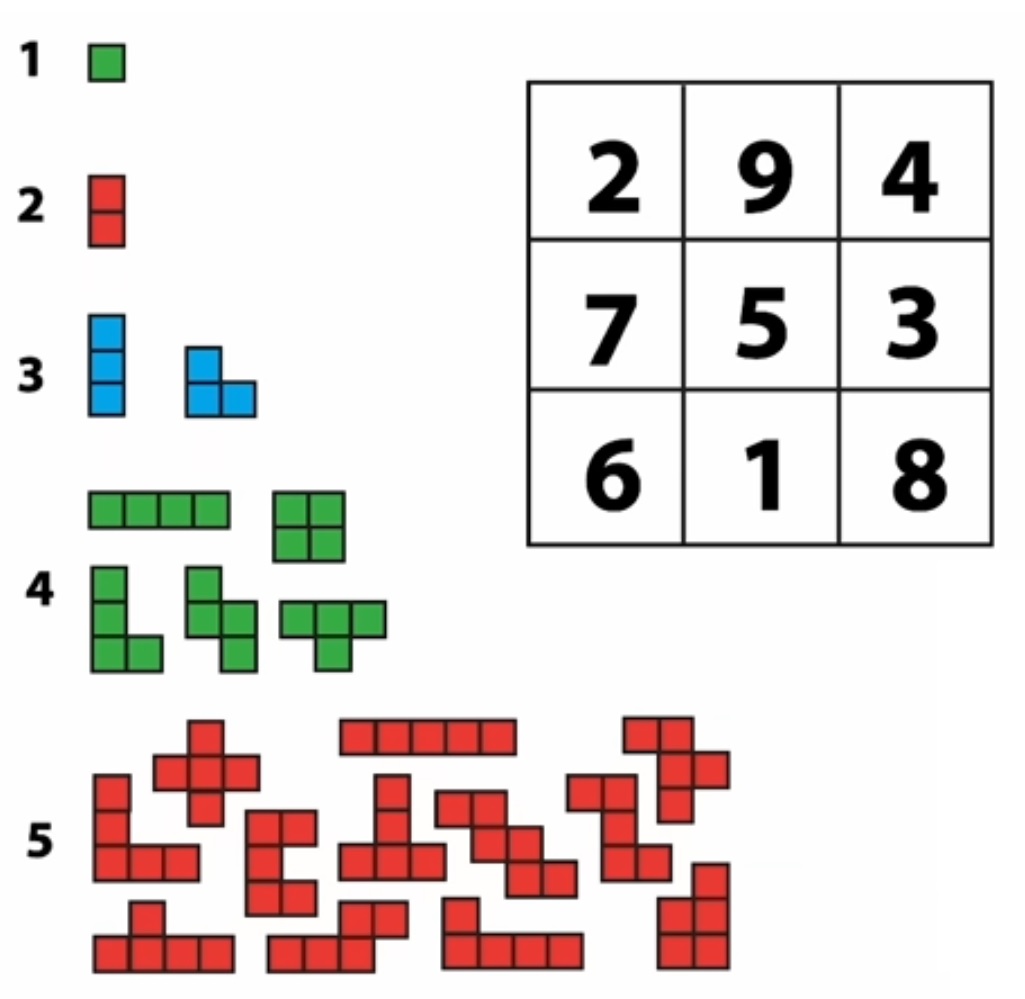
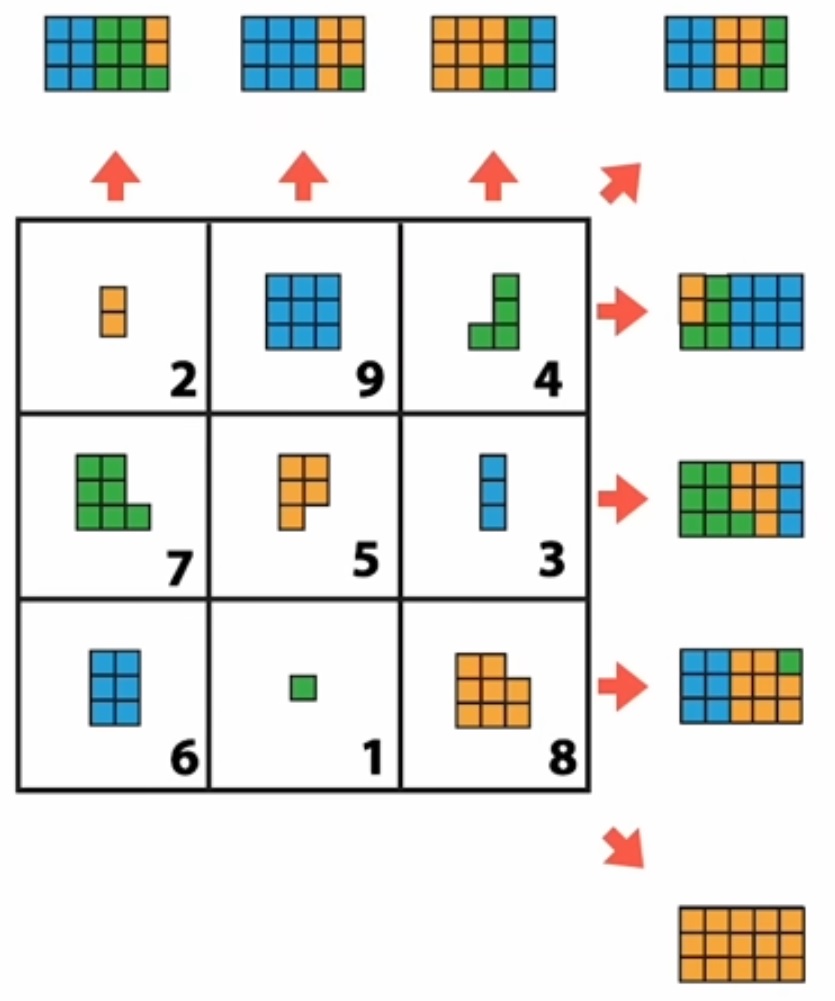
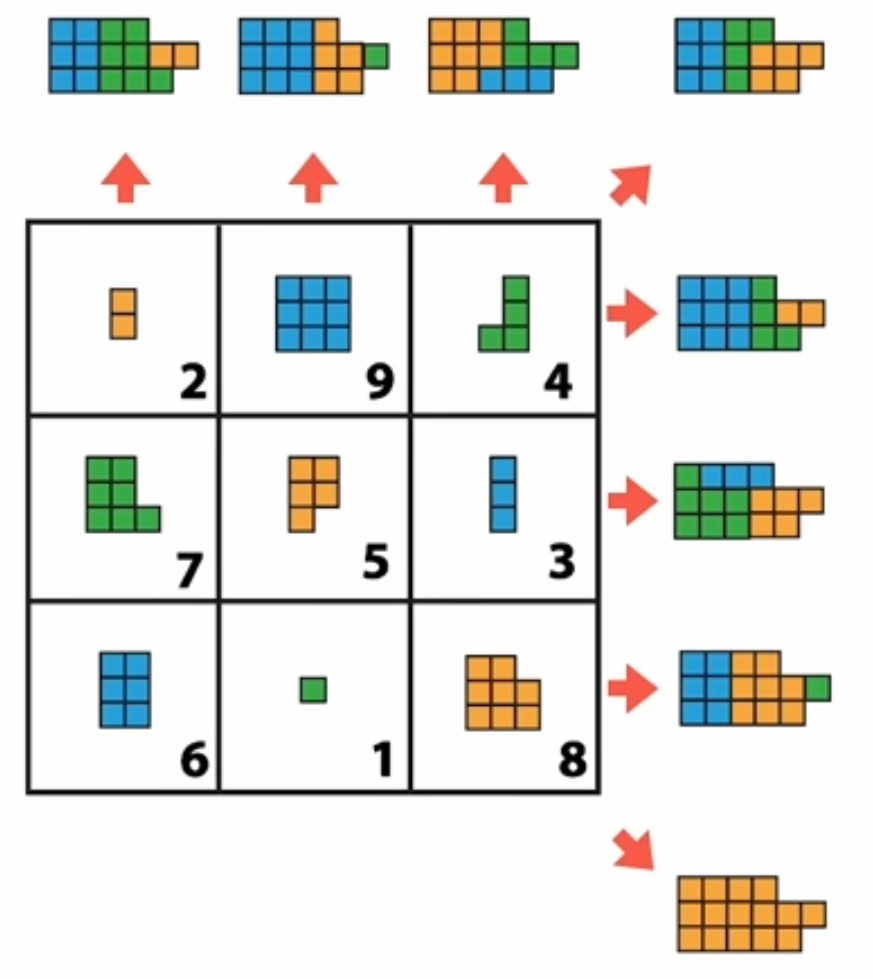
IV°/ Quadrillage carré :
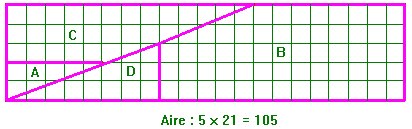
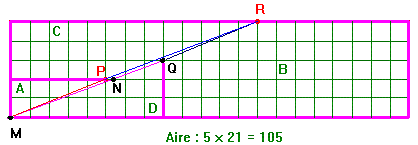
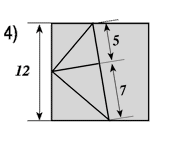
Une autre façon très simple de coder un message, avec un quadrillage carré :
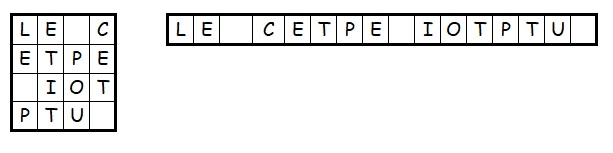 |
Il faut écrire le message sûr dans un quadrillage carré capable de contenir tout le message (compter les symboles, puis calculer la racine carrée de ce nombre. Le carré aura cette racine comme côté). Écrire le message dans cette matrice en commençant par la case en haut à gauche puis en descendant. Lire le message codé en commençant toujours par la case en haut à gauche puis en continuant vers la droite. |
V°/ Code alphabétique de Conway :
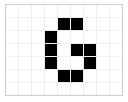
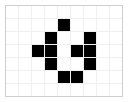
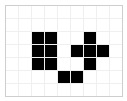
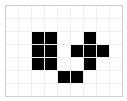
Vous connaissez certainement le jeu de la vie de Conway. Et pour construire un code de chiffrement, il suffit de dessiner une lettre de l’alphabet, G par exemple, et de lancer le jeu. On récupère la 3ième évolution que l’on simplifie et qui sera notre lettre codée.
| La lettre G de départ | 1ière évolution | 2ième évolution | 3ième évolution définitive |
 |
 |
 |
 |
Voici tous les symboles : Ecriture
| Lettres normales |  |
| 3ième évolution du jeu de la vie | |
| Ecriture simplifiée = code | |
| Lettres normales | |
| 3ième évolution du jeu de la vie | |
| Ecriture simplifiée = code | |
| Lettres normales | |
| 3ième évolution du jeu de la vie | |
| Ecriture simplifiée = code |
Un exemple :
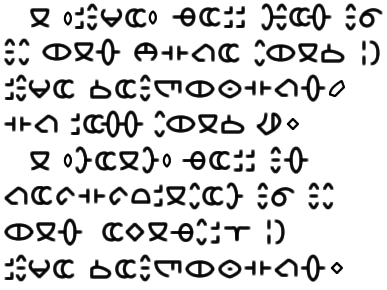 |
A ‘live’ cell dies if it has more than 3 live neighbors, or less than 2. A ‘dead’ cell is repopulated if it has exactly 3 live neighbors. |
VI°/ Code de César affine :
Au lieu de passer d’une lettre à une autre en additionnant un nombre entier, on multiplie par un nombre a puis on additionne par un autre nombre b. Pour jouer avec ce code allez voir le programme SCRATCH.
Le cryptage est facile. Il suffit de fabriquer un tableau de chiffrement où la position de chaque lettre à coder est multipliée par le premier nombre a puis on additionne le nombre b. Soit x le rang de la lettre à coder, le rang y de la lettre codée sera donnée par la formule : y = ax + b.
Pour le décryptage c’est plus compliqué car il faut gérer des nombres entiers et non décimaux.
C’est pour cette raison qu’il vaut mieux prendre les valeurs 3, 7 ou 9 pour le coefficient a. Dans ce cas là, les formules de décryptages spnt les suivantes :
| Coefficient a | Lettre y codée : y = ax + b | Lettre x de départ |
| 3 | y = 3x + b | x = 9y + (-bx9) [mod 26] |
| 7 | y = 7x + b | x = 15y + (-bx15) [mod 26] |
| 9 | y = 9x + b | x = 3y + (-bx3) [mod 26] |
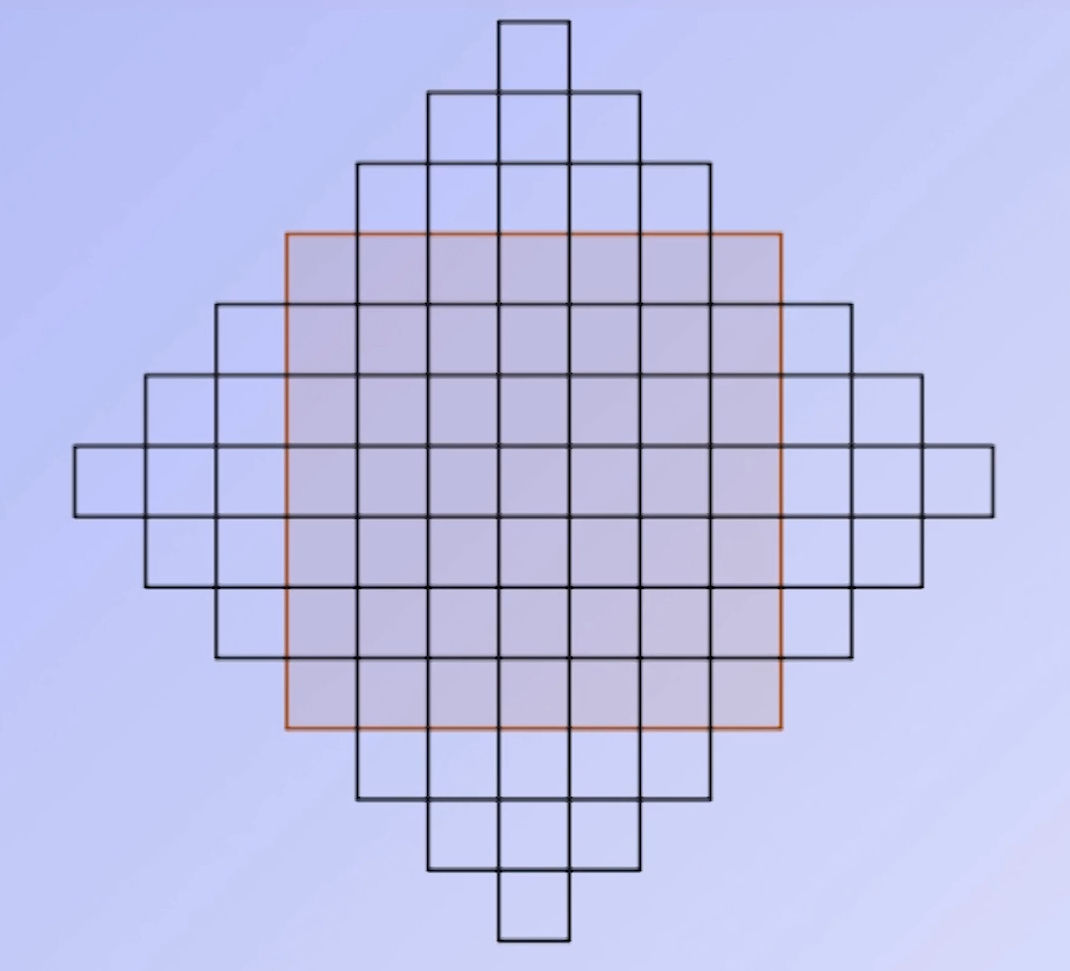
VII/ Les grilles tournantes du colonel Fleissner :
Les grilles tournantes est une méthode de cryptographie popularisée par le colonel autrichien Fleissner dans son livre Handbuch der Kryptographie. Il est difficile de savoir s’il en est réellement l’inventeur (des procédés de chiffrement par grille étaient utilisés depuis fort longtemps), mais son nom est resté attaché à cette méthode car Jules Verne, en 1885, a repris cette méthode de cryptographie dans son roman Mathias Sandorf, en l’attribuant à Fleissner.
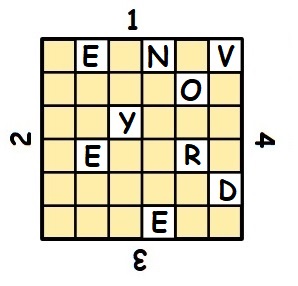
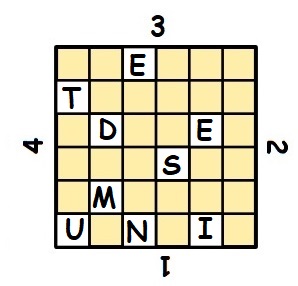
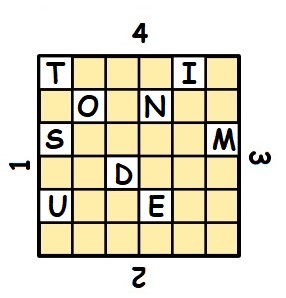
Par exemple, comment coder ENVOYER DES RENFORTS ET DES MUNITIONS :
 |
 |
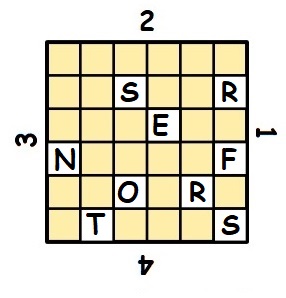 |
| Dans une grille 6×6, on découpe 9 carreaux. | On écrit ensuite le message dans les cases vides. | Puis on fait pivoter la grille d’un quart de tour vers la droite. |
 |
 |
 |
| Puis d’un autre quart. | Et enfin d’un dernier quart. On complète la grille par des lettres au hasard. Ici MDUE. | On obtient le message final suivant. |
On peut créer des grilles de toutes tailles, et même en utiliser plusieurs si le message est trop long. On peut aussi choisir de faire pivoter la grille vers la gauche. Pour jouer avec ce code allez voir le programme SCRATCH.
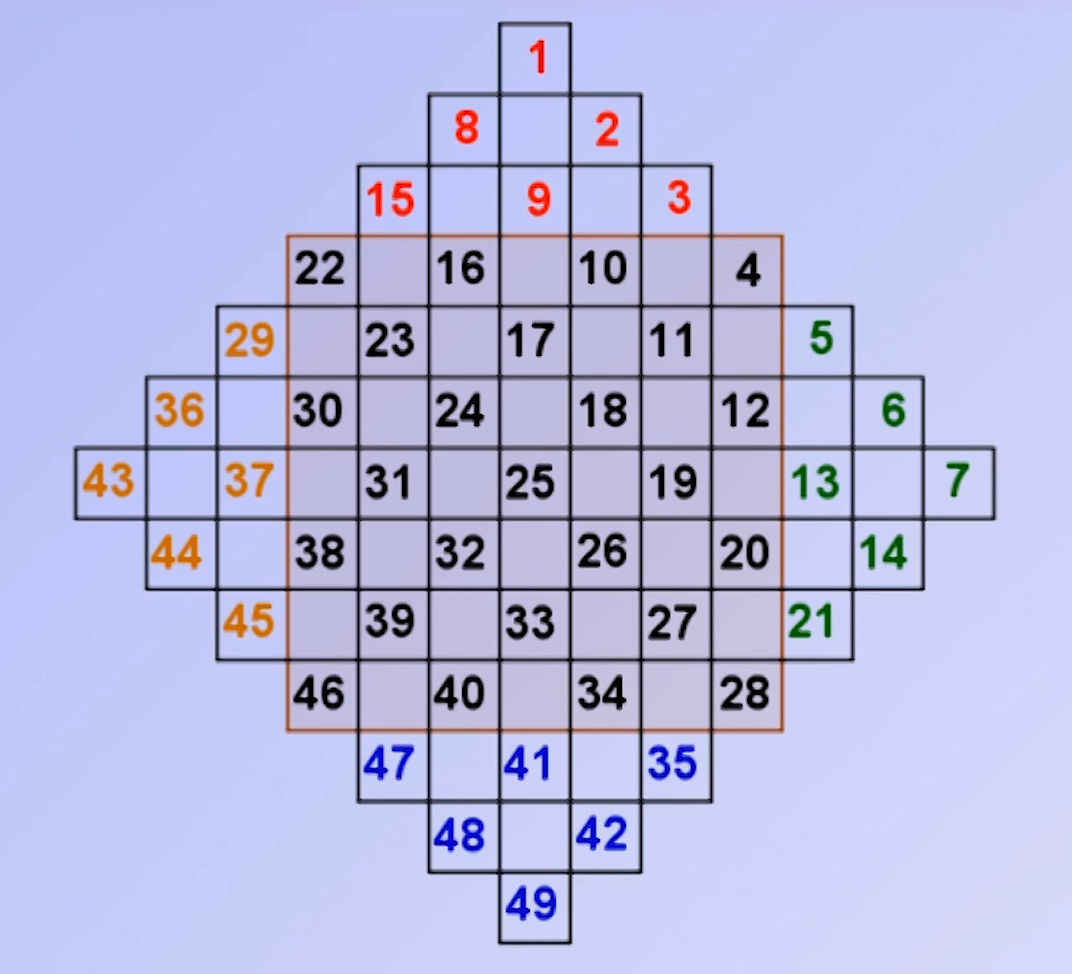
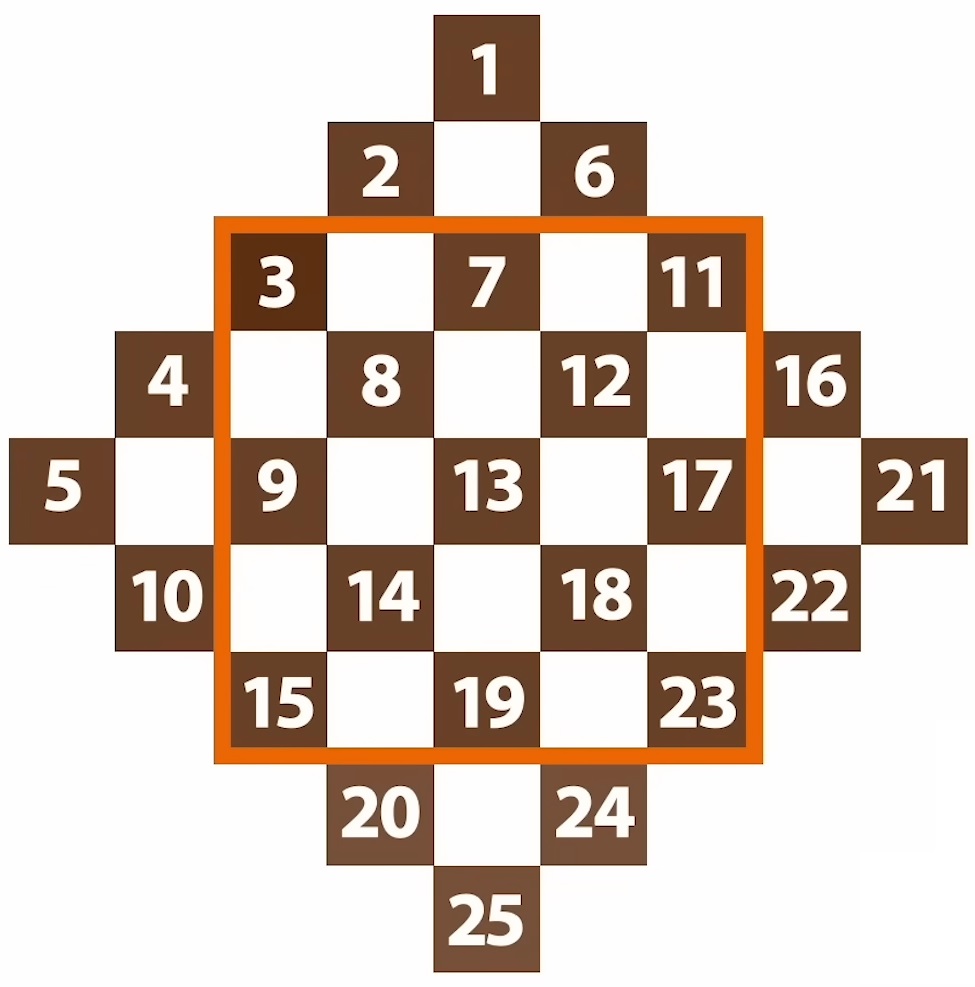
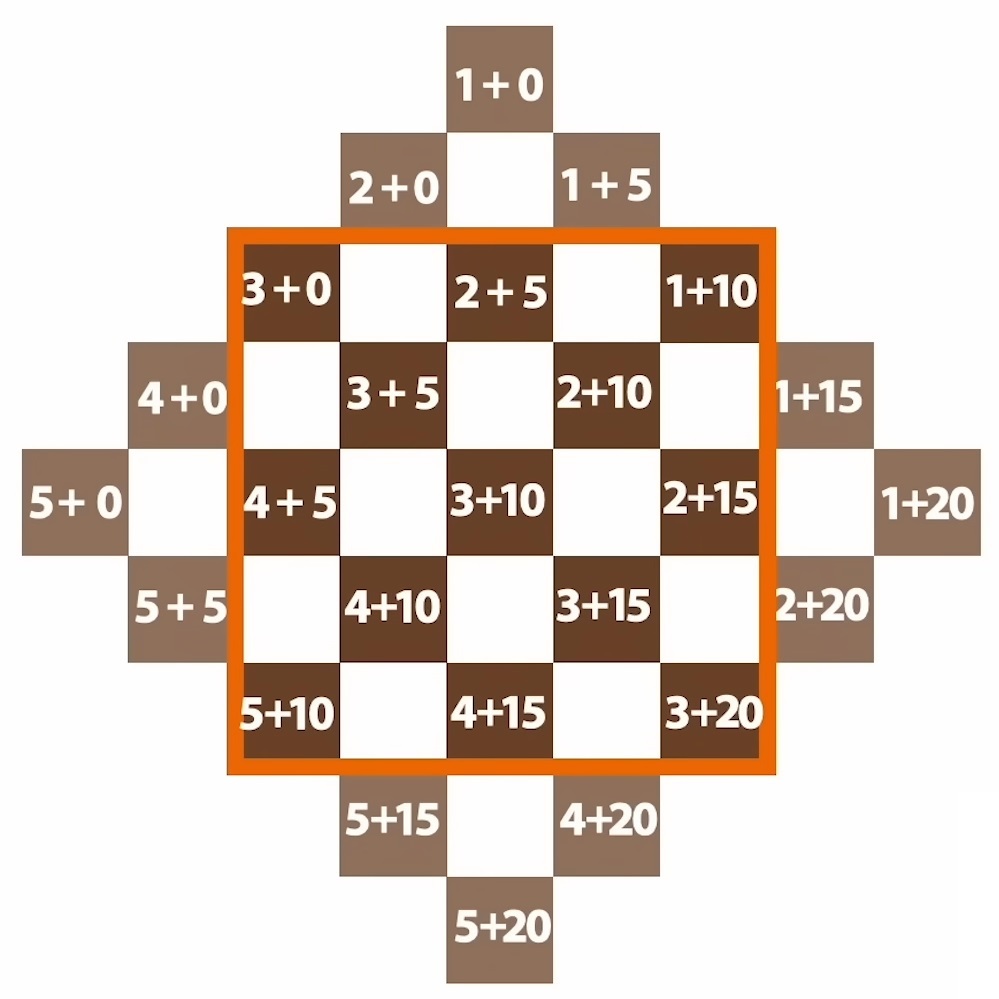
La découpe de la grille de départ ne se fait pas n’importe comment. En effet il ne faut pas que les cases vides retombent sur la même lettre. Pour cela on numérote les cases et on ne découpe qu’une lettre à chaque fois. Pour la grille 5×5 on utilisera pas la case centrale X.
 |
 |




























































 Le jeu de la vie dans le jeu de la vie.
Le jeu de la vie dans le jeu de la vie.








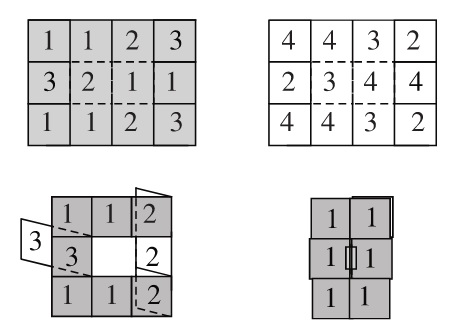
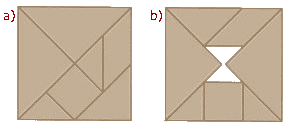
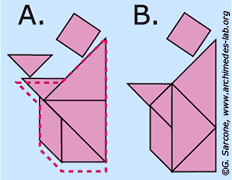
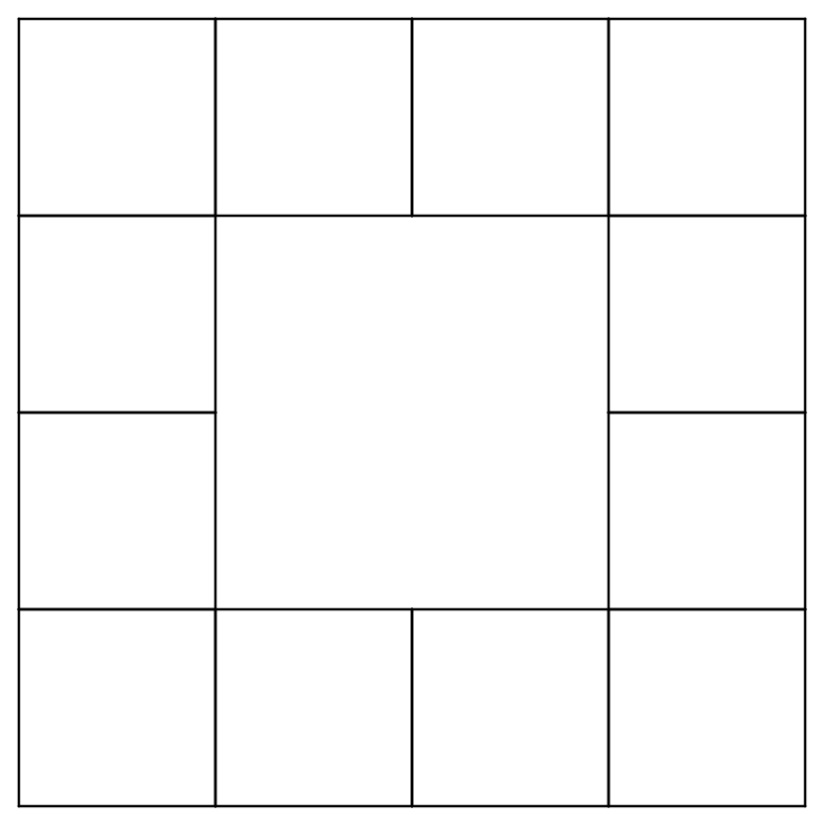 Le patron de l’hexatétraflexagone.
Le patron de l’hexatétraflexagone.
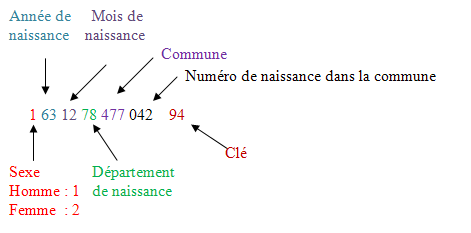





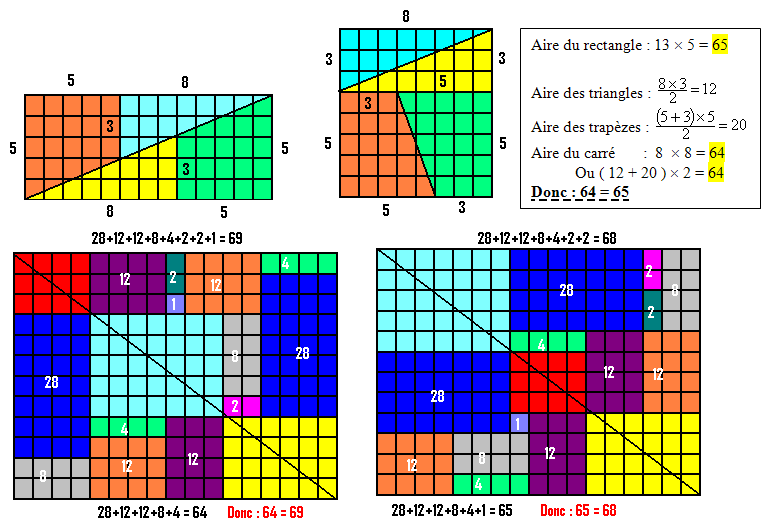
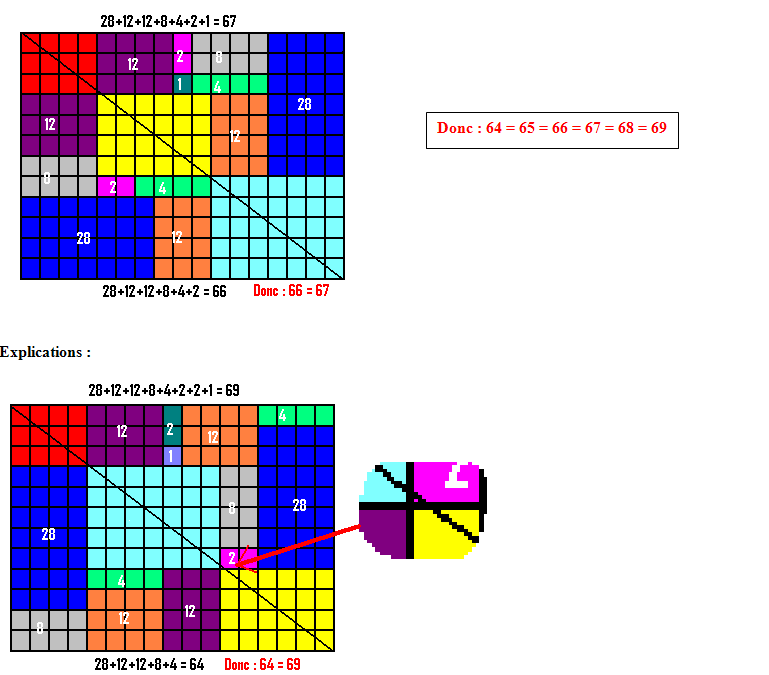
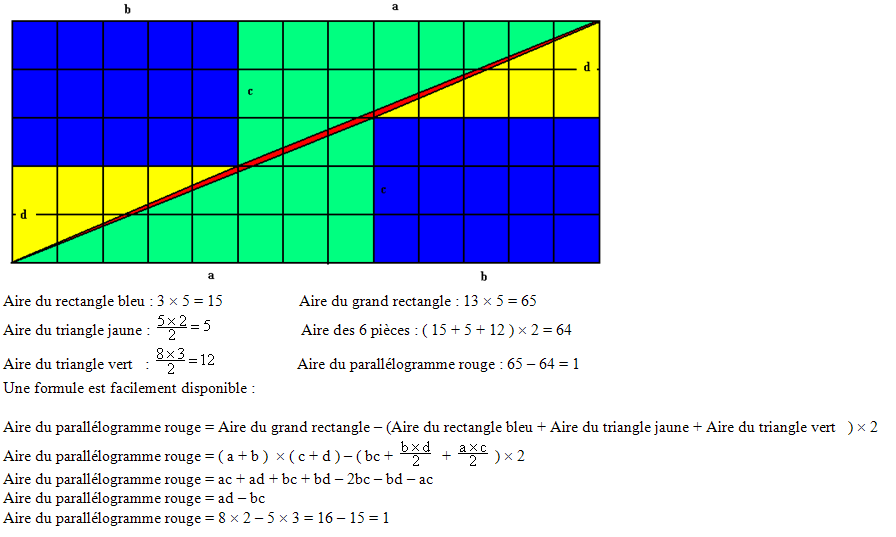
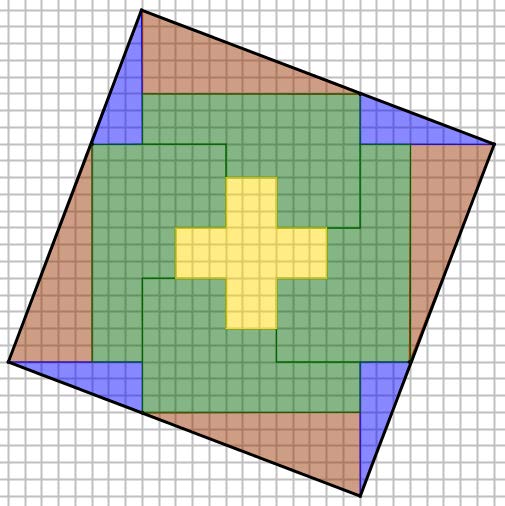
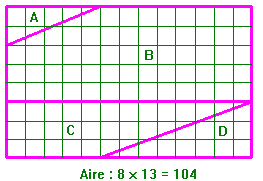
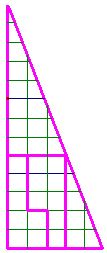
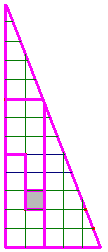
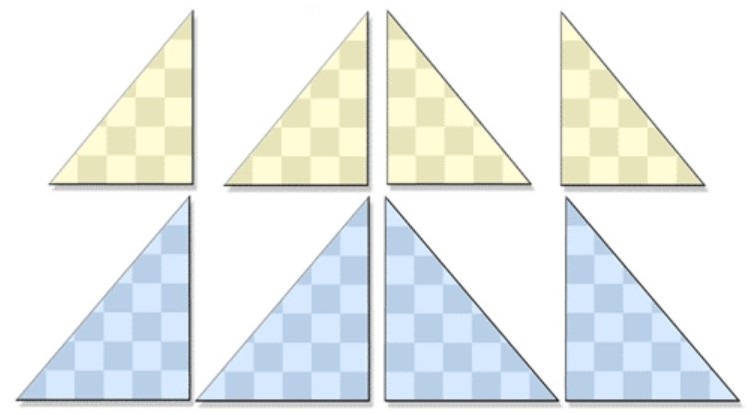
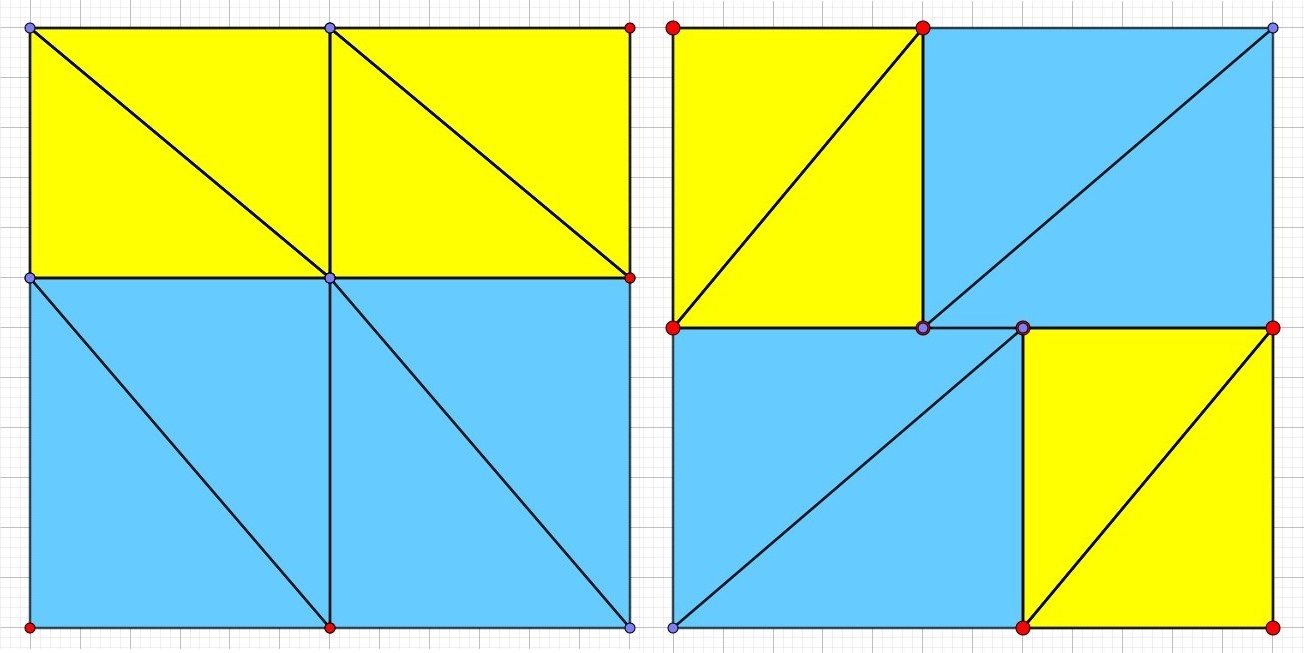
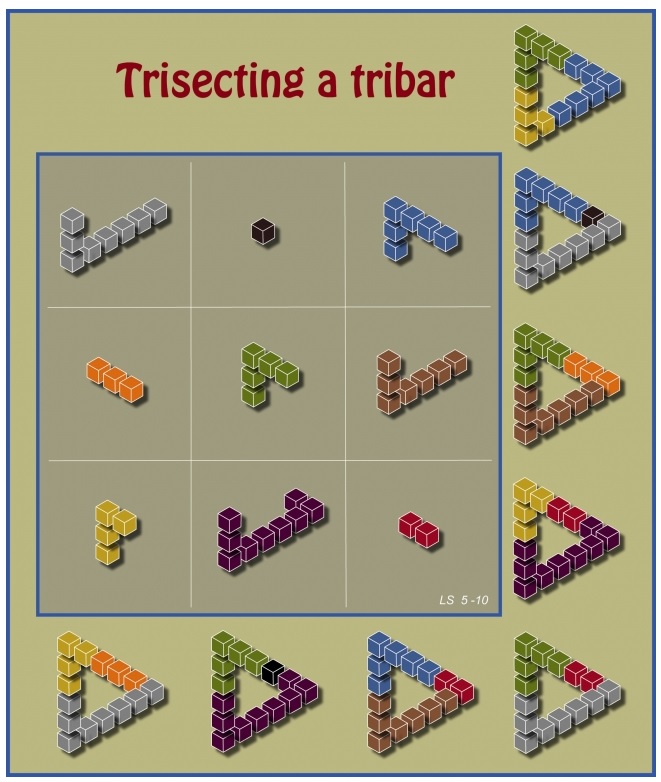
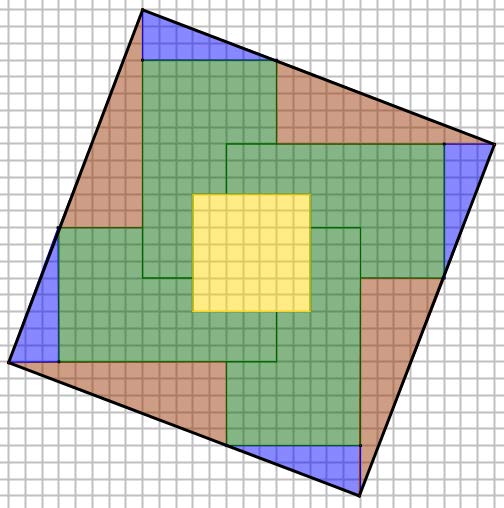 Avec les mêmes 13 pièces, voici un carré.
Avec les mêmes 13 pièces, voici un carré.