Les Maths sont bizarres

XVIII°/ Les graphes :

par

Un graphe est un ensemble points reliés par des arêtes qui peuvent être droites ou pas. Si les arêtes ne se croisent pas on dit que le graphe est planaire.

La formule d’Euler pour les graphes convexes : S + R = A + 2 (S nombre de sommets, R nombre de régions délimitées par les arêtes et A nombre d’arêtes)

1 points + 1 points = + 1 arêtes, donc pas de changement dans la formule. + 1 région sans sommet = + 1 arête
Schéma
Sommet S S = 1 S + 1 = 1 + 1 = 2 S + 4 = 5 S = 5
Régions R R = 1 R = 1 R = 1 R = 2 + 1 = 3
Arêtes A A = 0 A + 1 = 0 + 1 = 1 A + 4 A = 5 + 1 = 6
Formule d’Euler
S + R = A + 2		 1 + 1 = 0 + 2 = 2 2 + 1 = 1 + 2 = 3
S + 1 + R = A + 1 + 2
S + R = A + 2		 5 + 1 = 4 + 2 = 6
S + 4 + R = A + 4 + 2
S + R = A + 2		 5 + 3 = 6 + 2 = 8
S + R + 1 = A + 1 + 2
S + R = A + 2

Tour de magie :

Cette formule permet de créer un petit tour de magie assez bluffant : gribouiller n’importe comment. La seule chose qui importe, c’est que le gribouillage soit en un seul morceau (connexe). Par exemple, vous pouvez faire un truc comme ça :

C’est maintenant qu’on va faire des maths ! Dans ce gribouillage, on peut repérer des « Sommets » S (les points d’intersection et les extrémités), des « Arrêtes » A (ce qui relie deux sommets) et des « Régions » R (les cellules, délimitées par des arrêtes. Au passage, l’extérieur de la figure est une face. On les appellent souvent Face F.). Comptez-les !

Moi, je compte S = 26 sommets (bleus), A = 49 arrêtes (rouges) et F = 25 faces (verts)

Attention, tour de magie qui n’impressionnera personne. Je suis sûr que si vous effectuez l’opération S – A + F = 26 – 49 + 25 = 2, vous trouverez toujours 2 !

La formule d’Euler pour les polyèdres convexes : S + F = A + 2 (S nombre de sommets, F nombre de faces et A nombre d’arêtes).

Une très belle vidéo :

Vertices = sommets

Edges = arêtes

Faces = faces

Dans un polyèdre : Nombre de sommet – Nombre d’arêtes  + Nombre de face = 2

S – A + F = 2

Ou en Anglais : V – E + F = 2

XVII°/ Le triangle de Pascal :

par

Ce n’est pas Blaise Pascal (1623 – 1662) qui l’a trouvé mais il fut nommé ainsi en son l’honneur. Il est connu sous l’appellation « triangle de Pascal » en Occident, bien qu’il fût étudié par d’autres mathématiciens, parfois plusieurs siècles avant lui, en Inde, en Perse, au Maghreb, en Chine (où il est appelé « triangle de Yang Hui »), en Allemagne et en Italie.

I°/ Construction :
II°/ Coefficients des égalités remarques : coefficients binomiaux
III°/ La combinatoire : C’est l’art de compter les objets, actions ou autre.
IV°/ Trouver les puissances de 2 :
V°/ Trouver les puissances de 11 :
VI°/ La suite Fibonacci :
VII°/ La règle de la crosse de hockey :
VIII°/ Le triangle de Sierpinski :
IX°/ Les nombres premiers :

Sa construction est simple, mais ses applications sont multiples.

I°/ Construction :

On part du nombre 1 et à chaque ligne on rajoute un nombre qui est la somme des 2 nombres qui sont au-dessus de lui. Chaque case est donc la somme des 2 cases qui sont au-dessus, s’il n’y a pas de case on prend le nombre 0. Donc dans chaque ligne, le premier et le dernier nombre est 1.

1 1
2 1 1
3 2 = 1 + 1 1 2 1
4 1 3 3 1
5 4 = 1 + 3 1 4 6 4 1
6 1 5 10 10 5 1
7 1 6 15 20 15 6 1
8 35 = 15 + 20 1 7 21 35 35 21 7 1
9 1 8 28 56 70 56 28 8 1
10 1 9 36 84 126 126 84 36 9 1
11 1 10 45 120 210 252 210 120 45 10 1
12 1 11 55 165 330 462 462 330 165 55 11 1
13 1 12 66 220 495 792 924 792 495 220 66 12 1
14 1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
15 3003 = 1287 + 1716 1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
16 1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
17 1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
18 1 17 136 680 2380 6188 12376 19448 24310 24310 19448 12376 6188 2380 680 136 17 1
19 1 18 153 816 3060 8568 18564 31824 43758 48620 43758 31824 18564 8568 3060 816 153 18 1
20 1 19 171 969 3876 11628 27132 50388 75582 92378 92378 75582 50388 27132 11628 3876 969 171 19 1
21 1 20 190 1140 4845 15504 38760 77520 125970 167960 184756 167960 125970 77520 38760 15504 4845 1140 190 20 1
22 1 21 210 1330 5985 20349 54264 116280 203490 293930 352716 352716 293930 203490 116280 54264 20349 5985 1330 210 21 1
23 1 22 231 1540 7315 26334 74613 170544 319770 497420 646646 705432 646646 497420 319770 170544 74613 26334 7315 1540 231 22 1
24 1 23 253 1771 8855 33649 100947 245157 490314 817190 1144066 1352078 1352078 1144066 817190 490314 245157 100947 33649 8855 1771 253 23 1

Chaque case est la somme des 2 cases qui sont au-dessus. C’est-à-dire que le kième terme de la nième ligne est égal au (k-1)ième terme de la (n-1)ième ligne plus le kième terme de la (n-1)ième ligne

Voilà comment on l’écrit plus simplement.

C_{n}^{k}=C_{n-1}^{k-1}+C_{n-1}^{k} ou avec l’écriture Française \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k}

remarque :
C_{n}^{k}=\frac{n!}{k!(n - k)!}
n! = 1 x 2 x 3 x 4 x…x (n – 1) x n
(n + 1)! = (n + 1) x n!
(n - 1)! = \frac{n!}{n}

Démonstration :

(n-1)!= \frac{n!}{n} \frac{n!}{k!\times (n-k)!}=\frac{(n-1)!}{(k-1)!\times(n-1-k+1)!}+\frac{(n-1)!}{k!\times(n-1-k)!} \frac{n!}{k!\times (n-k)!}=\frac{\frac{n!}{n}}{\frac{k!}{k}\times(n-k)!}+\frac{\frac{n!}{n}}{k!\times \frac{(n-k)!}{(n-k)}} \frac{n!}{k!\times (n-k)!}=\frac{\frac{n!}{n}\times k}{k!\times(n-k)!}+\frac{\frac{n!}{n}\times (n-k)}{k!\times (n-k)!} \frac{n!}{k!\times(n-k)!}=\frac{n!(\frac{k}{n}+\frac{n-k}{n})}{k!\times (n-k)!} \frac{n!}{k!\times (n-k)!}=\frac{n!(\frac{k+n-k}{n})}{k!\times (n-k)!} \frac{n!}{k!\times (n-k)!}=\frac{n!}{k!\times (n-k)!}

donc : C_{n}^{k}=C_{n-1}^{k-1}+C_{n-1}^{k}

On peut aussi dire que, la somme des 2 cases est égale à celle qui est en dessous de celle de droite. C’est-à-dire que le kième terme de la nième ligne plus le (k+1)ième terme de la nième ligne et égal au le (k+1)ième terme de la (n+1)ième ligne

C_{n}^{k}+ C_{n}^{k+1}= C_{n+1}^{k+1} ou avec l’écriture Française \binom{n}{k}+\binom{n}{k+1}=\binom{n+1}{k+1}

\frac{n!}{k!\times (n-k)!}+\frac{n!}{(k+1)!\times (n-k-1)!}=\frac{(n+1)!}{(k+1)!\times (n+1-k-1)!} \frac{n!}{k!\times (n-k)!}+\frac{n!}{(k+1)\times k! \times \frac{(n-k)!}{(n-k)}}=\frac{(n+1)!}{(k+1)!\times (n-k)!} \frac{n!}{k!\times (n-k)!}+\frac{n!\times (n-k)}{(k+1) \times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1) \times k! \times (n-k)!} \frac{n!(k+1)+n!(n-k)}{(k+1)\times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1)\times k!\times (n-k)!} \frac{n!(k+1+n-k)}{(k+1)\times k!\times (n-k)!}=\frac{(n+1)\times n!}{(k+1)\times k!\times (n-k)!} \frac{n!(1+n)}{(k+1)k!(n-k)!}=\frac{(n+1)n!}{(k+1)k!(n-k)!}

.

II°/ Coefficients des égalités remarques : les coefficients binomiaux.

Il s’agit de développer l’expression (a+b) à l’exposant n, ou n est un entier naturel.

Par exemple : (a+b)² = a² + 2ab + b²

Et bien le triangle de Pascal permet de déterminer les coefficients de chaque membre de l’égalité. Pour cela il faut prendre les coefficients de la ligne (n-1) et élever a et b aux puissances successives.

(a + b)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k} \ b^{k}

Formule du binôme de Newton

 \binom{n}{k} = C_{n}^{k}=\frac{n!}{k! (n - k)!)}

Coefficients de la (n-1)ième ligne du triangle de Pascal.
1 (a + b) 0 = 1
1 1 (a + b) 1 = 1a + 1b
1 2 1 (a + b) 2 = 1a² +2ab + 1b²
1 3 3 1 (a + b) 3 = 1a3 + 3a²b + 3ab² + 1b3
1 4 6 4 1 (a + b) 4 = 1a4 + 4a3b + 6a²b² + 4ab3 + 1b4
1 5 10 10 5 1 (a + b) 5 = 1a5 + 5a4b + 10a3b² + 10a²b3 + 5ab4 + 1b5
1 6 15 20 15 6 1 (a + b) 6 = 1a6 + 6a5b + 15a4b² + 20a3b3 + 15a²b4 + 6ab5 + 1b6

III°/ La combinatoire : C’est l’art de compter les objets, actions ou autre.

Par exemple, combien y-a-t ’il de façon de choisir k objets parmi n. Et bien ce nombre sera égal au (k+1)ième coefficient de la (n-1)ième ligne du triangle de Pascal

1 1
2 1 1
3 1 2 1
4 1 3 3 1
5 1 4 6 4 1
6 1 5 10 10 5 1
7 1 6 15 20 15 6 1
Combien y-a-t ‘il de façon de choisir 2 objets parmi 4 objets a, b, c et d : le (2 + 1) = 3ième nombre de la (4 + 1) = 5ième ligne, c’est-à-dire 6.

Voici les 6 couples que l’on peut faire : a-b ; a-c ; a-d ; b-c ; b-d ; c-d
Combien y-a-t ‘il de façon de choisir 3 objets parmi 6 objets : le (3 + 1) = 4ième nombre de la (6 + 1) = 7ième ligne, c’est-à-dire 20.

C_{3}^{6} = \frac{6!}{3!(6 - 3)!)}= \frac{6 \times 5\times4\times3\times2}{3\times2\times3\times2}= 5 \times4 =20

Bien entendu il existe une formule qui permet de trouver ce résultat sans avoir à fabriquer le triangle de Pascal :

Le nombre de choix possible pour choisir k éléments parmi n est égal à : C_{n}^{k} = \frac{n!}{k!(n - k)!)}

donc :

Choix de 2 éléments parmi 4 (le (2 + 1) = 3ième nombre de la (4 + 1) = 5ième ligne) = C_{4}^{2} = \frac{4!}{2!(4 - 2)!)}= \frac{4\times3\times2}{2\times2}= 3 \times 2= 6

Choix de 3 éléments parmi 6 (le (3 + 1) = 4ième nombre de la (6 + 1) = 7ième ligne) = C_{6}^{3} = \frac{6!}{3!(6 - 3)!)}= \frac{6 \times 5\times4\times3\times2}{3\times2\times3\times2}= 5 \times4 =20

IV°/ Trouver les puissances de 2 :

Si on additionne tous les nombres de la ligne n on obtient 2n-1.

n Somme 2n-1
1 1 1 2^0
1 1 2 2 2^1
1 2 1 3 4 2^2
1 3 3 1 4 8 2^3
1 4 6 4 1 5 16 2^4
1 5 10 10 5 1 6 32 2^5
1 6 15 20 15 6 1 7 64 2^6
1 7 21 35 35 21 7 1 8 128 2^7
1 8 28 56 70 56 28 8 1 9 256 2^8
1 9 36 84 126 126 84 36 9 1 10 512 2^9
1 10 45 120 210 252 210 120 45 10 1 11 1024 2^10
1 11 55 165 330 462 462 330 165 55 11 1 12 2048 2^11
1 12 66 220 495 792 924 792 495 220 66 12 1 13 4096 2^12
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1 14 8192 2^13
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1 15 16384 2^14
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1 16 32768 2^15
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1 17 65536 2^16
1 17 136 680 2380 6188 12376 19448 24310 24310 19448 12376 6188 2380 680 136 17 1 18 131072 2^17
1 18 153 816 3060 8568 18564 31824 43758 48620 43758 31824 18564 8568 3060 816 153 18 1 19 262144 2^18
1 19 171 969 3876 11628 27132 50388 75582 92378 92378 75582 50388 27132 11628 3876 969 171 19 1 20 524288 2^19
1 20 190 1140 4845 15504 38760 77520 125970 167960 184756 167960 125970 77520 38760 15504 4845 1140 190 20 1 21 1048576 2^20
1 21 210 1330 5985 20349 54264 116280 203490 293930 352716 352716 293930 203490 116280 54264 20349 5985 1330 210 21 1 22 2097152 2^21
1 22 231 1540 7315 26334 74613 170544 319770 497420 646646 705432 646646 497420 319770 170544 74613 26334 7315 1540 231 22 1 23 4194304 2^22
1 23 253 1771 8855 33649 100947 245157 490314 817190 1144066 1352078 1352078 1144066 817190 490314 245157 100947 33649 8855 1771 253 23 1 24 8388608 2^23

Démonstration : d’après la formule du binôme de Newton

(a + b)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}\ b^{k}

Si on prend a = b = 1 on a :

(1 + 1)^{n}=2^{n}= \sum_{k=0}^{n}\binom{n}{k}\times 1^{n-k} \times 1^{k}= \sum_{k=0}^{n}\binom{n}{k}

Donc 2n est égal à la somme des termes d’une ligne du triangle de Pascal.

V°/ Trouver les puissances de 11 :

C’est un peu plus compliqué et fastidieux. Les nombres du triangle de Pascal représentent les coefficients des puissances de 10 successives.

VI°/ La suite Fibonacci :

Cette suite célèbre est constituée en partant de 0 puis 1. On obtient les nombres suivants en additionnant les deux nombres précédents.

0 ; 1 ; 1 = 0 + 1 ; 2 = 1 + 1; 3 = 2 + 1 ; 5 = 3 + 2 ….

Et bien en additionnant les diagonales ascendantes comme sur la figure ci-dessous, on obtient la suite Fibonacci.

Vous aurez ici une merveilleuse horloge de Fibonacci.

Une autre merveille : et si on attribuait une note pour chaque chiffre et que l’on jouait la suite de Fibonacci, cela donnerait quoi ?

John Edmark s’amuse avec Fibonacci dans des constructions de toutes beautés.

Lorsqu’elle est filmée à 24 images par seconde et tournée à 550 tours par minute, chaque image représente une rotation de 137,5 degrés, ce qui équivaut à l’angle d’or.

 

VII°/ La règle de la crosse de hockey :

Si on ajoute les nombres qui se suivent dans une diagonale, on obtient cette somme en bas à droite de la diagonale.

VIII°/ Le triangle de Sierpinski :

Si on enlève les nombres pairs du triangle Pascal on obtient celui de Sierpinski.

Triangle de Sierpinski Triangle de Pascal Les deux

IX°/ Les nombres premiers :

Le triangle de Pascal peut nous donner certains nombres premiers, avec une manipulation un peu fastidieuse, mais qui démontre qu’il y a une infinité de nombres premiers.

Voici le début du triangle de Pascal. Remplaçons les nombres pairs par 0 et les impairs par 1. Rapprochons les nombres. On obtient des nombres binaires. Traduisons les nombres binaires en nombres décimaux. Dès que l’on a un nombre premier, il faut le multiplier successivement à tous les résultats précédents avant de retrouver un nouveau nombre premier.

X°/ Multiple de n de la nième ligne :

Une propriété assez étrange est que si pour la nième ligne, n est un nombre premier, alors cette ligne ne contient que des multiples de n, en enlevant les deux 1.

Par exemple, à la 7ième ligne, il n’y a que des multiples de 7 : 7, 21 et 35.

XIX°/ Les triplets Pythagoricien :

par

Un triplet pythagoricien, ou triplet de Pythagore, est un ensemble de 3 nombres entiers naturels non nuls vérifiant le théorème de Pythagore : a² + b² = c². Le triplet pythagoricien le plus connu est (3, 4, 5).

Il en existe une infinité et l’intérêt est de trouver une méthodes pour les trouver tous.

I°/ La suite de Fibonacci :
II°/ Le triplet (3n,4n,5n) :
III°/ Généralisation :
IV°/ Une autre formule :
V°/ Des triplets très particuliers :

I°/ La suite de Fibonacci :

Il existe une infinité de triplets Pythagoricien. On peut en retrouver certains grâce à la suite de Fibonacci.

Pour rappel, la suite de Fibonacci consiste à partir du nombre 0 puis 1, et à additionner les nombres deux à deux à l’infini :

1 1 2 3 5 8 13 21 … ( en effet : 1  0 + 1 = 1  1 + 1 = 2  1 + 2 = 3  2 + 5 = 5 …)

Pour trouver quelques nombres Pythagoriciens, il suffit de prendre 4 nombres qui se suivent dans la suite de Fibonacci et d’effectuer les calculs suivants :

Soient w, x, y et z, 4 nombres la suite de Fibonacci et a, b et c les triplets Pythagoricien : a = wz ; b = 2xy et c = wy + xz.

La suite Fibonacci :
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711
w x y z

Utilisons les nombres la suite de Fibonacci :

Les triplets Pythagoriciens :
w=1 ; x=1 ; y=2 ; z=3 w=1 ; x=2 ; y=3 ; z=5 w=2 ; x=3 ; y=5 ; z=8 w=3 ; x=5 ; y=8 ; z=13 w=5 ; x=8 ; y=13 ; z=21 w=8 ; x=13 ; y=21 ; z=34 w=13 ; x=21 ; y=34 ; z=55
a = wz 1×3 = 3 1×5 = 5 2×8 = 16 3×13 = 39 5×21 = 105 8×34 = 272 13×55 = 715
b = 2xy 2x1x2 = 4 2x2x3 = 12 2x3x5 = 30 2x5x8 = 80 2x8x13 = 208 2x13x21 = 546 2x21x34 = 1428
c = wy + xz 1×2 + 1×3 = 5 1×3 + 2×5 = 13 2×5 + 3×8 = 34 3×8 + 5×13 = 89 5×13 + 8×21 = 233 8×21 + 13×34 = 610 13×34 + 21×55 = 1597
Théorème de Pythagore :
a² + b² = 3² + 4² = 25 5² + 12² = 169 16² + 30² = 1156 39² + 80² = 7921 105² + 208² = 54289 272² + 546² = 372100 715² + 1428² = 2550409
c² = 5² = 25 13² = 169 34² = 1156 89² = 7921 233² = 54289 610² = 372100 1597² = 2550409

Démonstration : 4 nombres la suite de Fibonacci w, x, y = w + x et z = x + y = x + w + x = 2x + w

triplets Pythagoricien a, b et c : c² = a² + b²

c² = (wy + xz)² = w²y² + 2wxyz + x²z² = w²(w + x)² + 2wx(w + x)(2x + w) + x²(2x + w)² = w²(w² + 2wx + x²) + 2wx(2wx + w² + 2x² + wx) + x²(4x² + 4wx + w²)

= w4 + 2w3x + w²x² +  4w²x² + 2w3x + 4wx3 + 2w²x² + 4x4 + 4wx3 + w²x² = w4 + 4x4 + 4w3x + 8wx3 + 8 w²x²

a² + b²= w²z² + 4x²y² = w²(2x + w)² + 4x²( w + x)² = w²(4x² + 4wx + w²) + 4x²(w² + 2wx + x²) = 4w²x² + 4w3x + w4 + 4w²x² + 8wx3 + 4x4 = w4 + 4x4 + 4w3x + 8wx3 + 8w²x²

II°/ Le triplet (3n,4n,5n) :

Le triplet le plus connu est (3, 4, 5) : en effet 3² + 4² = 9 + 16 = 25 = 5².

De fait, les triplets de la forme (3n, 4n ,5n) sont aussi pythagoricien : (3n)² + (4n)² = 9n² + 16n² = 25n² = (5n)².

III°/ Généralisation :

On peut en trouver d’autre : 5² + 12² = 25 + 144 = 169 = 13² et leur variantes : (5n)² + (12n)² = 25n² + 144n² = 169n² = (13n)².

Tout triplet pythagoricien (a,b,c) peut s’obtenir de la façon suivante : Choisir trois entiers naturels quelconques u,v et n, avec u strictement plus grand que v, et poser :

a = n × (u² − v²)
b = n × 2uv
c = n × (u² + v²)

Voici quelques exemples :
u v n a b c a² b² a²+ b² c²
2 1 1 3 4 5 9 16 25 25
2 1 2 6 8 10 36 64 100 100
2 1 3 9 12 15 81 144 225 225
3 2 2 10 24 26 100 576 676 676
2 1 5 15 20 25 225 400 625 625
3 2 1 5 12 13 25 144 169 169
10 5 2 150 200 250 22500 40000 62500 62500

IV°/ Une autre formule :

Il existe une formule « magique » et très élégante qui permet trouver une infinité de triplet.

x+\frac{x}{2x+1}=\frac{2x^{2}+2x}{2x+1}
x représente un nombre entier et (2x+1) le nombre impair qui suit son double, comme 1 et 3 ou 5 et 11.
Le triplet Pythagoricien sera donné par le numérateur (2x²+2x), le dénominateur (2x+1) et le numérateur plus un (2x²+2x+1).
Par exemple, avec x = 4 : 4 + 4/9 = 40/9 ; les nombres 40 et 9 sont les côtés d’un triangle rectangle et l’hypoténuse égale au plus grand côté plus 1 (40 + 1 = 41).
                                 En effet : 9² + 40² = 1 681 = 41²
Il est a noter que si on construit la progression en commençant par x = 1, (2x+1) représentera la suite de tous les nombres impairs.
x 2x+1 x+x/(2x+1) Numérateur 2x²+2x Dénominateur 2x+1 Hypoténuse 2x²+2x+1 Num²+ Dén² Hypo²
1 3 1 + 1/3 = 4/3 4 3 5 25 25
2 5 2 + 2/5 = 12/5 12 5 13 169 169
3 7 3 + 3/7 = 24/7 24 7 25 625 625
4 9 4 + 4/9 = 40/9 40 9 41 1681 1681
5 11 5 + 5/11 = 60/11 60 11 61 3721 3721
6 13 6 + 6/13 = 84/13 84 13 85 7225 7225
7 15 7 + 7/15 = 112/15 112 15 113 12769 12769
8 17 8 + 8/17 = 144/17 144 17 145 21025 21025

Cherchez des triplets :

V°/ Des triplets très particuliers :

1°/ Un triplet compliqué :

Voici un triangle rectangle avec des côtés rationnels (le côté le plus long a un dénominateur de 45 chiffres !) et une aire de 157 a été découvert par Don Zagier en 1993.

2°/ Une hypoténuse paradoxale de longueur nulle :

Un étrange triangle rectangle impliquant le nombre imaginaire unitaire i.

Le carré du  nombre complexe i est égal à -1, donc :

i² + 1 ² = -1 + 1 = 0 !!!!!!!

C’est bien sûr n’importe quoi, mais c’est amusant.

3°/ Un triangle rectangle magique :

Un triangle avec des côtés π (3,14), e (2,71) et le nombre d’or (1,61) est presque un triangle rectangle !

 4°/ Triangle de Kepler :

Un triangle de Kepler est un triangle rectangle formé de trois carrés dont les aires sont en progression géométrique selon le nombre d’or.

Ce triangle a pour côté 1,\sqrt{\varphi} et \varphi, donc on a bien : \sqrt{\varphi}^{2}+1^{2}=\varphi+1=\varphi^{2}
Traçons le cercle circonscrit au triangle de Kepler dont le diamètre est l’hypoténuse du triangle.
Les périmètres du carré (4\sqrt{\varphi} ≈ 5,0884) et du cercle (2\pi R=2\pi\frac{\varphi}{2}=\pi\varphi ≈ 5,083) sont presque égaux avec une erreur inférieure à 0,1 %.De là, nous pouvons obtenir la coïncidence d’approximation :

4\sqrt{\varphi}=\pi\varphi\Rightarrow\pi=\frac{4\sqrt{\varphi}}{\varphi}=\frac{4}{\sqrt{\varphi}}

5°/ Triangle rectangle de Fibonacci :

La somme des carrés de nombres de Fibonacci consécutifs est un autre nombre de Fibonacci.

 

XVI°/ Coder un message :

par

De tout temps les hommes ont cherché à protéger leurs messages des yeux indiscrets. Pour cela ils ont redoublé d’imagination pour chiffrer leurs messages.

I°/ Programme SCRATCH :
II°/ Historique :
III°/ Écriture Betamaze :
IV°/ Quadrillage carré :
V°/ Code alphabétique de Conway :
VI°/ Code de César affine :
VII/ Les grilles tournantes du colonel Fleissner :

I°/ Programme SCRATCH :

Voici un programme Scratch pour s’amuser à coder et décoder.

Exemple : codons Le petit Poucet (le mot de passe est entre les parenthèses).

Texte clair L E P E T I T P O U C E T
César (5) Q J U J Y N Y U T Z H J Y
Atbash O V K V G R G K L F X V G
Alphabet désordoné I Y G Y N C N G D R E Y N
Mot-clef (mathweb) I W N W R D R N L S T W R
Quadrillage L T O T E I U P T C E P E
Code d’Alberti L F R H X N Z W W D M P F
Vigenere (mathadore) X E I L T L H G S G C X A
César affine (35) O T A T M F M A X P N T M
Symétrie (stpaul) Q K X K Y G Y X B R N K Y

II°/ Historique :

Voici un florilège des méthodes de chiffrement les plus connues.

Codage Date Méthode Avantages Inconvénients
Antiquité Antiquité – Xerxès veut envahir la Grèce, il rase la tête d’un esclave, écrit le message sur le crâne et laisse repousser les cheveux.
– Avaler le message écrit sur un tissu en soie enrobé de cire.
– Écrire le message sur le bois d’une tablette de cire, puis la recouvrir de cire.		 Le message est caché et les moyens sont simples et nombreux. Le message est en clair.
La scytale spartiate Vième Avt JC
On entoure une lanière de cuir autour d’un bâton, puis on écrit son message dans le sens de la longueur du bâton. On complète éventuellement avec des lettres au hasard pour remplir toute la lanière.  Le destinataire devra avoir un bâton du même diamètre.
Une fois la lanière déroulée le message est illisible et elle peut servir de ceinture et être ainsi complètement anodine. La protection n’est pas bien grande si on connait le procédé.
Le chiffre Atbash Les hébreux dès 500 av. JC Il consiste simplement à écrire l’alphabet en sens contraire.

 

Texte clair A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Texte codé Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

LEPETITPOUCET = OVKVGRGKLFXVG

 Le message est crypté et peu de gens savent lire. Une fois la méthode connue, le message est clair. Or, certaines lettres sont plus fréquentes que d’autres dans une langue, donc une simple analyse fréquentielle permet de casser le code. En Français le E est très présent, donc la lettre la plus fréquente du message est certainement le E.
Par exemple au Scrabble, certaines lettres valent plus de points que d’autres. Le Z vaut 10 points en France mais seulement 3 en Allemagne.
Le code de César Entre Ier et IX IXème siècle.
Et même par l’armée Russe en 1915		 Les lettres sont simplement décalées d’un nombre donné. Ici le 5.

 

Texte clair A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Texte codé F G H I J K L M N O P Q R S T U V W X Y Z A B C D E

LEPETITPOUCET = QJUJYNYUTZHJY
Un mot-clef   Prenons un mot-clé facile à retenir, mettons MATHWEB, et de compléter ensuite le tableau par ordre alphabétique. Ceci donne ici :

 

Texte clair A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Texte codé M A T H W E B C D F G I J K L N O P Q R S U V X Y Z

LEPETITPOUCET = IWNWRDRNLSTWR

 Seul le destinataire connait le

 

mot-clef.
Poly-alphabétique : le code d’Alberti 1404-1472 Alberti & Abbé Jean Triqueme Il faut créer une grille. L’alphabet sur la 1ière ligne, puis on décale d’une lettre par ligne. Le message à coder est sur la colonne rouge et on repère sa correspondance sur la ligne bleue. Ainsi, le (L ; L) = L et le (E ; E) = F

 

  A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
L A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
E B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
P C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
E D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
T E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
I F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
T G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
P H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
O I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
U J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
C K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
E L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
T M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
  N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
  O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
  P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
  Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
  R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
  S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
  T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
  U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
  V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
  W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
  X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
  Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
  Z A B C D E F G H I J K L M N O P Q R S T U V W X Y

LEPETITPOUCET = LFRHXNZWWDMPF

 La même lettre peut être codée par différentes lettres et inversement une lettre du message peut avoir plusieurs significations. Si on connait la méthode, cela devient un jeu d’enfant.
Le plus gros inconvénient c’est que l’abbé Triqueme a publié un livre sur sa méthode !!!
Poly-alphabétique avec une clef : le code de Vigenere Blaise de Vigenere 1523-1596 pendant 400 ans Même chose que le code d’Alberti mais avec une clef.

 

Texte clair L E P E T I T P O U C E T
La clef M A T H A D O R E M A T H
Codé X E I L T L H G S G C X A

C’est le couple lettre-clef et lettre-message qui code pour la lettre-code.
Ainsi, le (L ; M) = X et le (E ; A) = E

  A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z Z A B C D E F G H I J K L M N O P Q R S T U V W X Y

LEPETITPOUCET = XEILTLHGSGCXA

 C’est la même chose que le code d’Alberti mais avec une clef. L’ analyse fréquentielle ne sert plus à rien car la même lettre peut être codée par différentes lettres et inversement une lettre du message peut avoir plusieurs significations. Charles Babage (1805-1881) casse le code de Vigenere.
Machine Enigma 1945   1016 combinaison possibles. Code cassé par Alan turing. Le principal inconvénient était qu’une lettre ne pouvait pas être codée par elle-même.

Un site consacré au chiffrement. Gigantesque avec des outils automatiques : https://www.apprendre-en-ligne.net/crypto/index.html et sa section historique.

III°/ Écriture Betamaze :

Il existe beaucoup de façon de coder un message et certaines sont jolies et ludiques à défaut d’être performantes.

On peut par exemple utiliser la police d’écriture Betamaze, qui est très originale. On peut l’installer sur son ordinateur et l’utiliser dans Word par exemple (Télécharger la police).

IV°/ Quadrillage carré :

Une autre façon très simple de coder un message, avec un quadrillage carré :

Il faut écrire le message sûr dans un quadrillage carré capable de contenir tout le message (compter les symboles, puis calculer la racine carrée de ce nombre. Le carré aura cette racine comme côté).
Écrire le message dans cette matrice en commençant par la case en haut à gauche puis en descendant.
Lire le message codé en commençant toujours par la case en haut à gauche puis en continuant vers la droite.

V°/ Code alphabétique de Conway :

Vous connaissez certainement le jeu de la vie de Conway. Et pour construire un code de chiffrement, il suffit de dessiner une lettre de l’alphabet, G par exemple, et de lancer le jeu. On récupère la 3ième évolution que l’on simplifie et qui sera notre lettre codée.

La lettre G de départ 1ière évolution  2ième évolution 3ième évolution définitive

Voici tous les symboles : Ecriture 

Lettres normales
3ième évolution du jeu de la vie
Ecriture simplifiée = code
Lettres normales
3ième évolution du jeu de la vie
Ecriture simplifiée = code
Lettres normales
3ième évolution du jeu de la vie
Ecriture simplifiée = code

Un exemple :

A ‘live’ cell dies if it has more than 3 live neighbors, or less than 2. A ‘dead’ cell is repopulated if it has exactly 3 live neighbors.

VI°/ Code de César affine :

Au lieu de passer d’une lettre à une autre en additionnant un nombre entier, on multiplie par un nombre a puis on additionne par un autre nombre b. Pour jouer avec ce code allez voir le programme SCRATCH.

Le cryptage est facile. Il suffit de fabriquer un tableau de chiffrement où la position de chaque lettre à coder est multipliée par le premier nombre a puis on additionne le nombre b. Soit x le rang de la lettre à coder, le rang y de la lettre codée sera donnée par la formule : y = ax + b.

Pour le décryptage c’est plus compliqué car il faut gérer des nombres entiers et non décimaux.

C’est pour cette raison qu’il vaut mieux prendre les valeurs 3, 7 ou 9 pour le coefficient a. Dans ce cas là, les formules de décryptages spnt les suivantes :

Coefficient a Lettre y codée : y = ax + b Lettre x de départ
3 y = 3x + b x = 9y + (-bx9) [mod 26]
7 y = 7x + b x = 15y + (-bx15) [mod 26]
9 y = 9x + b x = 3y + (-bx3) [mod 26]

VII/ Les grilles tournantes du colonel Fleissner :

Les grilles tournantes est une méthode de cryptographie popularisée par le colonel autrichien Fleissner dans son livre Handbuch der Kryptographie. Il est difficile de savoir s’il en est réellement l’inventeur (des procédés de chiffrement par grille étaient utilisés depuis fort longtemps), mais son nom est resté attaché à cette méthode car Jules Verne, en 1885, a repris cette méthode de cryptographie dans son roman Mathias Sandorf, en l’attribuant à Fleissner.

Par exemple, comment coder ENVOYER DES RENFORTS ET DES MUNITIONS :

Dans une grille 6×6, on découpe 9 carreaux. On écrit ensuite le message dans les cases vides. Puis on fait pivoter la grille d’un quart de tour vers la droite.
Puis d’un autre quart. Et enfin d’un dernier quart. On complète la grille par des lettres au hasard. Ici MDUE. On obtient le message final suivant.

On peut créer des grilles de toutes tailles, et même en utiliser plusieurs si le message est trop long. On peut aussi choisir de faire pivoter la grille vers la gauche. Pour jouer avec ce code allez voir le programme SCRATCH.

La découpe de la grille de départ ne se fait pas n’importe comment. En effet il ne faut pas que les cases vides retombent sur la même lettre. Pour cela on numérote les cases et on ne découpe qu’une lettre à chaque fois. Pour la grille 5×5 on utilisera pas la case centrale X.

 

 

II°/ Le nombre Pi : Un nombre célèbre et mystérieux.

par

I°/ Son utilité :

A°/ La géométrie :
B°/ La probabilité :
C°/ Les nombres premiers entre eux :
D°/ Les suites :
E°/ L’analyse :
F°/ La Bible :
G°/ Quelques belles formules faisant intervenir \pi   :

II°/ Son écriture : Pi-Search le site pour trouver des décimales


III°/ Son calcul :

A°/ A Babylone :
B°/ En Égypte :
C°/ En Grèce :

1°/ Démonstration de la formule de l’aire du disque :
2°/ Calcul du nombre \pi :

D°/ Époque moderne :
E°/ Le nombre Tau :

 IV°/Quelques histoires originales sur [latex] \pi [/latex] :

    A°/ un nombre univers :
    B°/ L’Indiana pi bill :
    C°/ La pyramide de Khéops :
    D°/ Amusons nous :

 

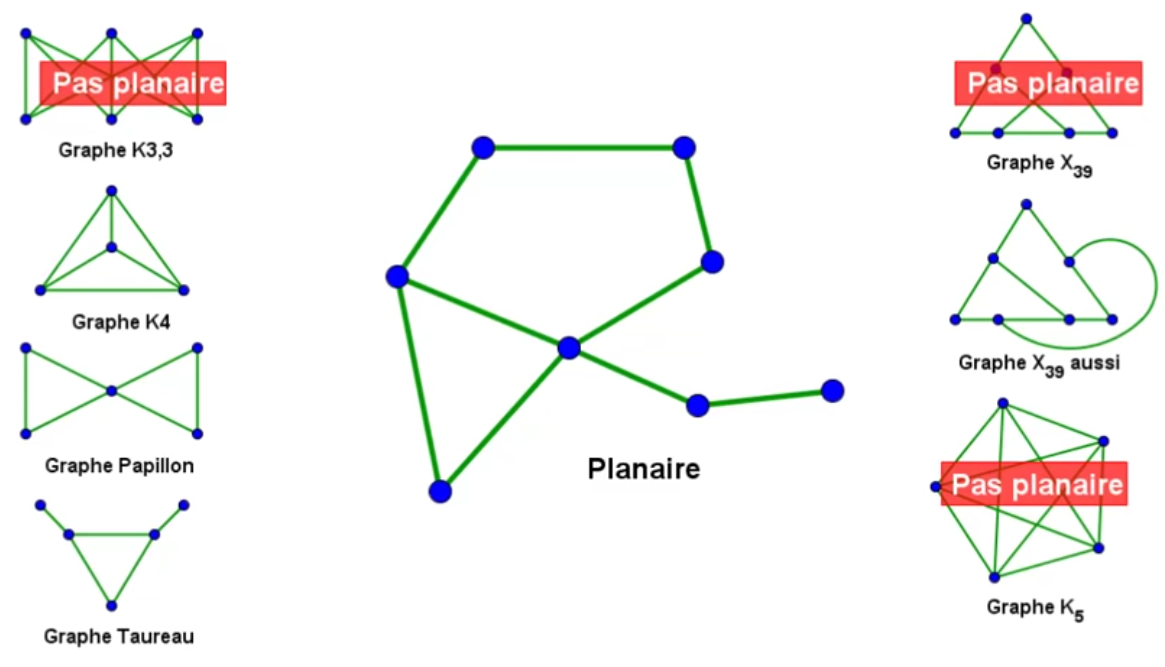
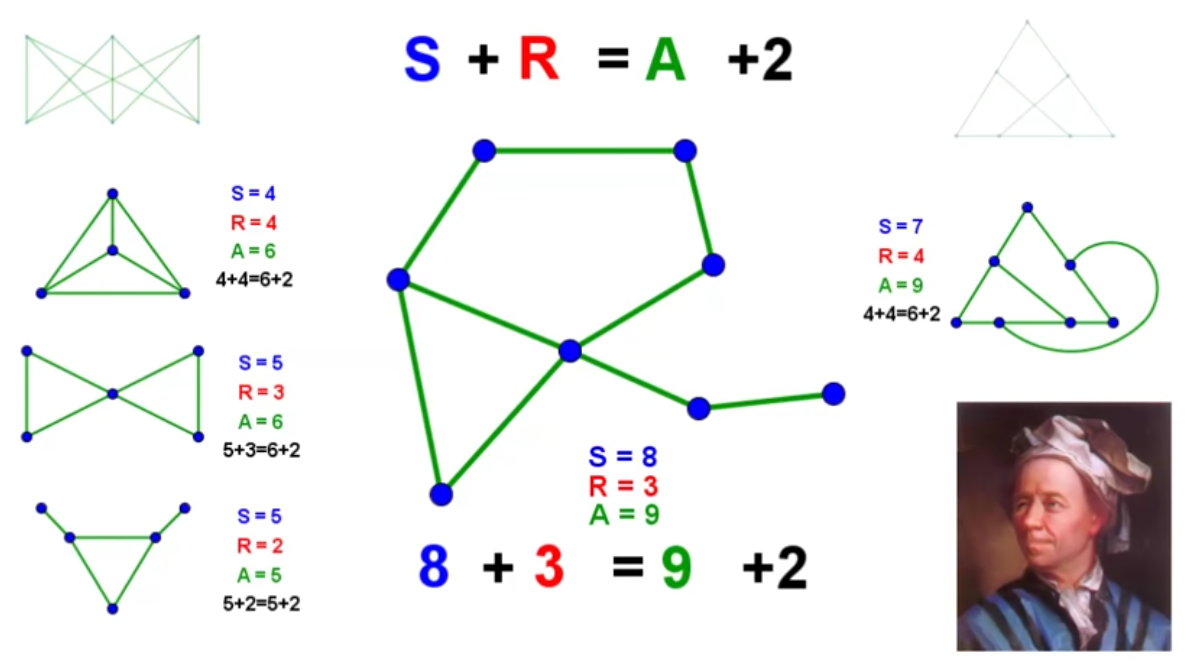
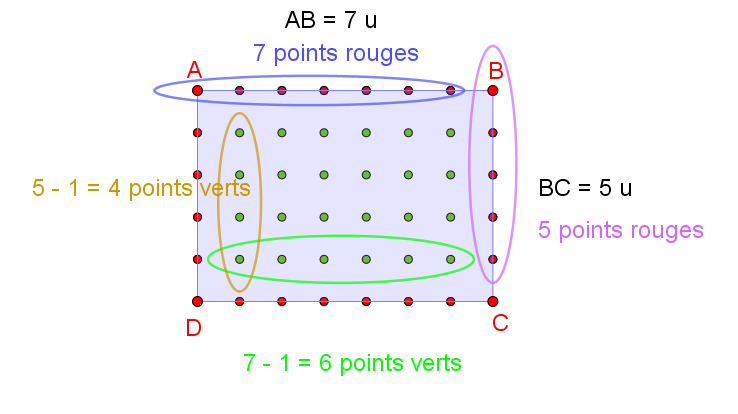
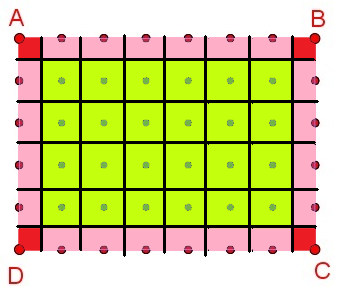
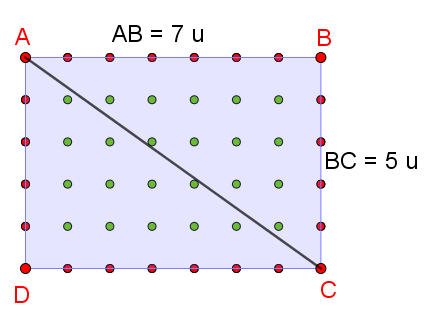
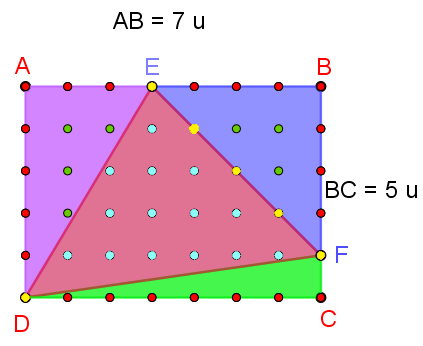
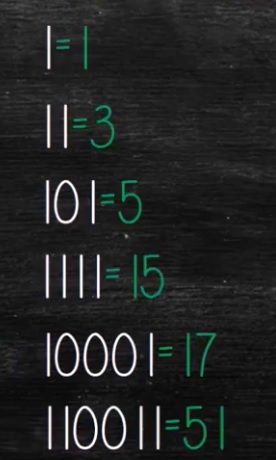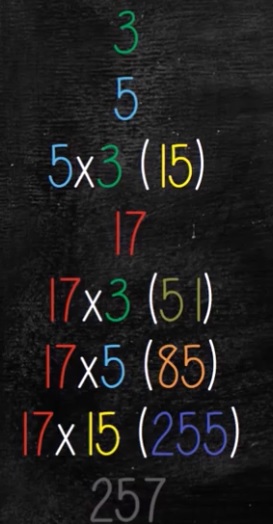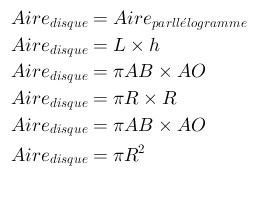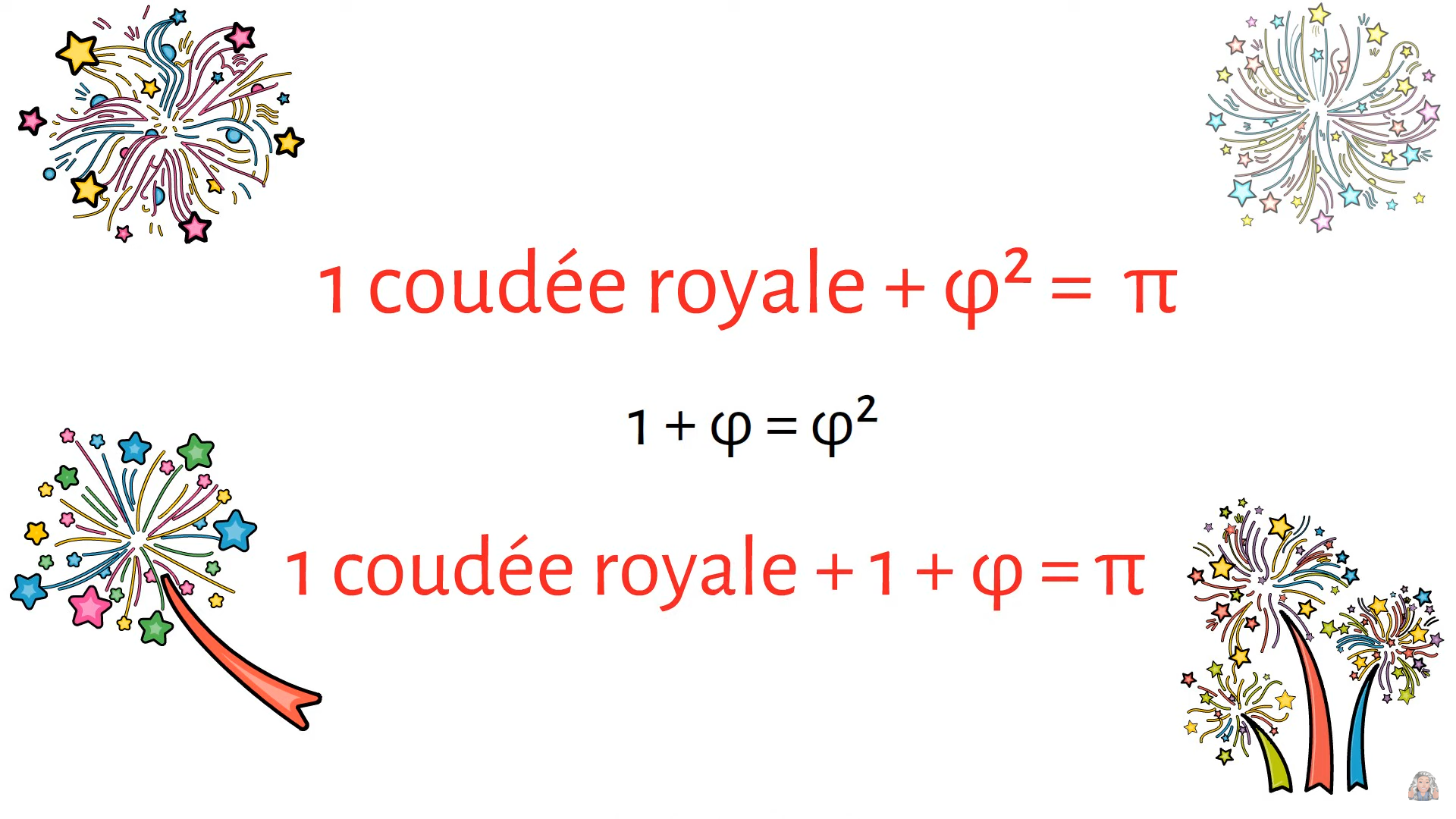I°/ Son utilité :

On retrouve le nombre \pi un peut partout dans les Mathématiques.

A°/ La géométrie :

Son utilité principale est de calculer la circonférence du cercle, l’aire du disque et le volume de la boule, mais aussi les ellipses.

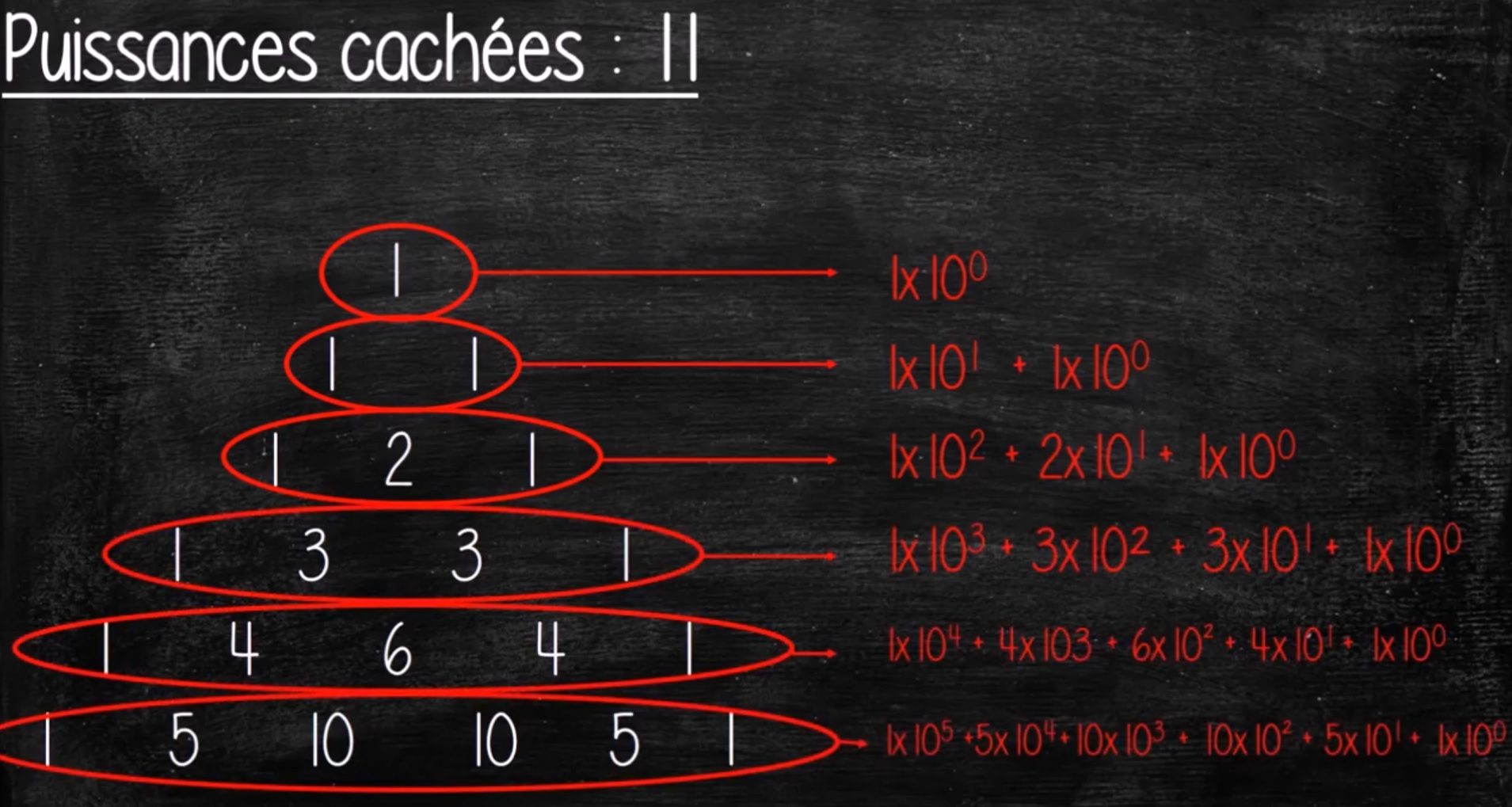
Circonférence du cercle = 2 \pi R
Aire du disque = \pi R^{2}
Volume boule = \frac{4}{3} \pi R^{3}

Une définition simple de est que ce nombre représente le périmètre d’un cercle de diamètre un.

Perimetre_{cercle}= 2\pi R = \pi \times D = \pi\times 1 = \pi

 

B°/ Les probabilités :

Au 18ième siècle, un grand mathématicien français du nom de George Buffon a réalisé l’expérience suivante. Il lance des aiguilles sur un parquet composés de lames rectangulaires. Si la longueur des aiguilles est égale à la largeur des lames de parquet, combien a t’on de chance qu’il y ai une aiguille qui se trouve à l’intersection de 2 lames et non à l’intérieur d’une lame ?

Il a démontrer que cette probabilité était de \frac{2} {\pi}

 

 

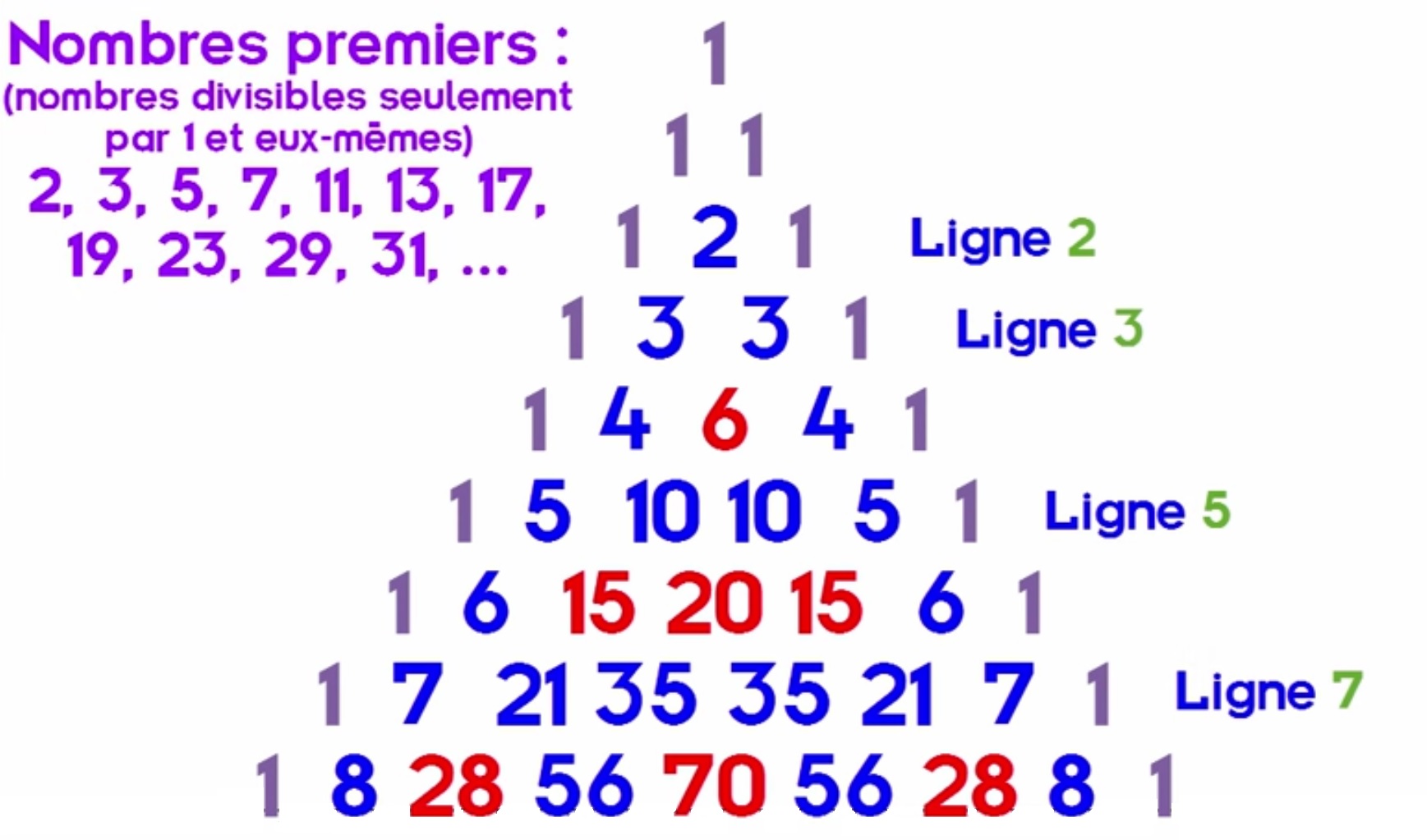
C°/ Les nombres premiers entre eux :

Un nombre premier est un nombre qui n’est divisible que par 1 ou par lui-même. Par exemple :

12 n’est pas premier car 12 = 3 x 4

23 est premier car 23 = 1 x 23 et c’est tout.

Deux nombres sont premiers entre eux s’ils n’ont pas de diviseur commun autre que 1, donc s’ils ne sont pas dans la même table de multiplication. Par exemple :

15 et 6 ne sont pas premiers entre eux car ils sont divisibles par 3.

15 et 4 sont premiers entre eux car ils ne sont divisibles que par 1.

Les mathématiciens se sont amusés a déterminer quelle proportion de couple de nombre était premiers entre eux (oui ils ont des jeux bizarre !!).

Cette proportion est de \frac{\pi^{2}}{6}

D°/ Les suites :

Si on ajoute tous les inverses des carrés on obtient un nombre qui sera égal à 1,644… qui représente le nombre \frac{\pi^{2}}{6}

\sum_{i=1}^{\infty }\frac{1}{i^{2}}=\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}...=\frac{\pi ^{2}}{6}

 

E°/ L’analyse :

C’est la branche des mathématiques qui traite explicitement de la notion de limite, que ce soit la limite d’une suite ou la limite d’une fonction.

Une définition du nombre \pi est :

\pi est le plus petit nombre réel a > 0 tel que cos(a) = -1

F°/ La Bible :

Dans le passage de la Bible 1. Rois 7.23 : « Il fit la Mer en métal fondu, de dix coudées de bord à bord, à pourtour circulaire de 5 coudées de hauteur ; un fil de 30 coudées en mesurait le tour »

Traduction : dix coudées de bord à bord donc un diamètre de 10 coudées
30 coudées en mesurait le tour donc un périmètre de 30 coudées

Donc pour dieu  : \pi = \frac{30}{10} = 3

G°/ Quelques belles formules faisant intervenir \pi   : La source




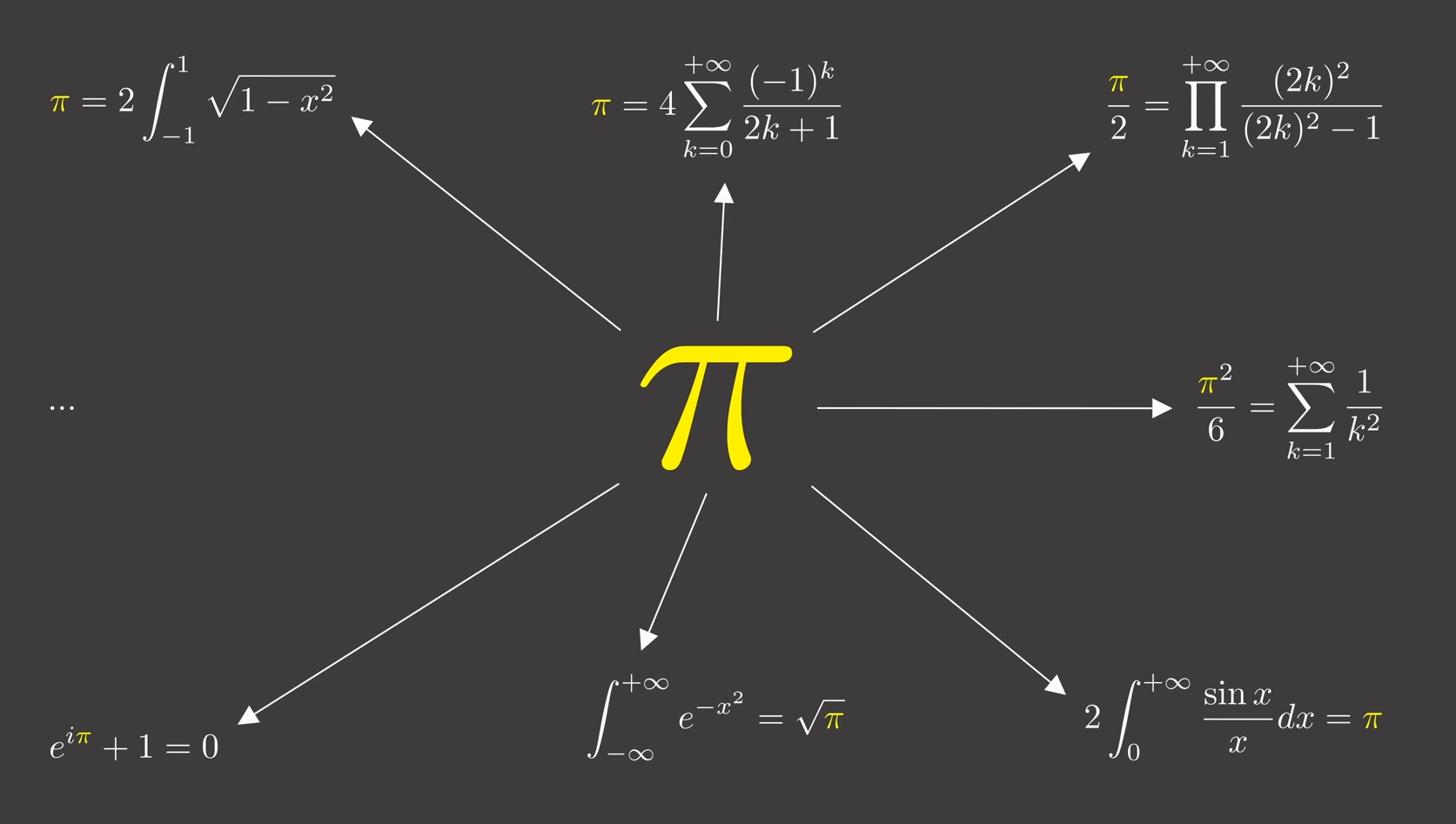
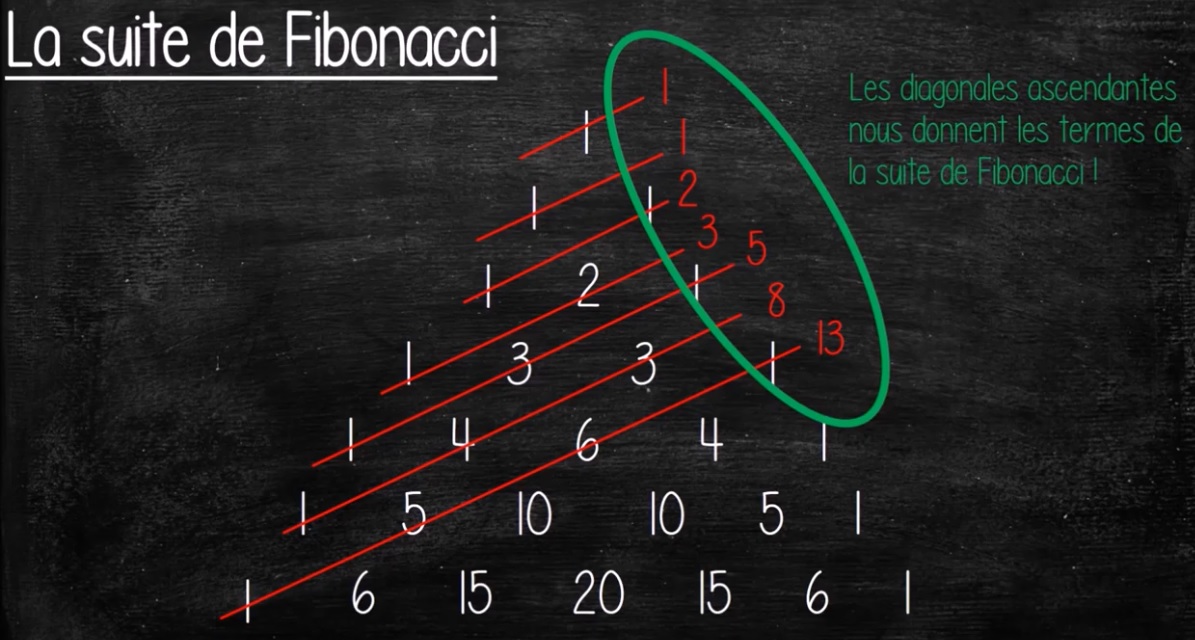
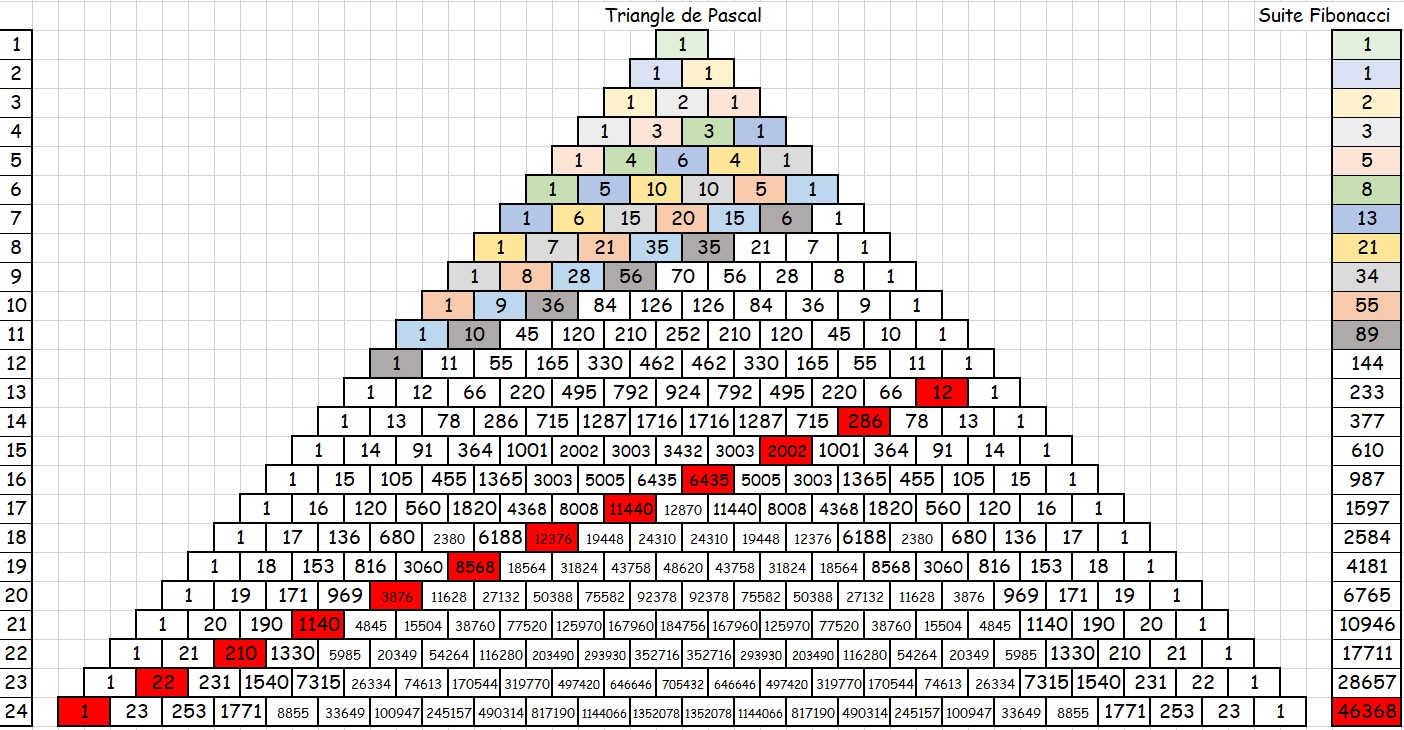
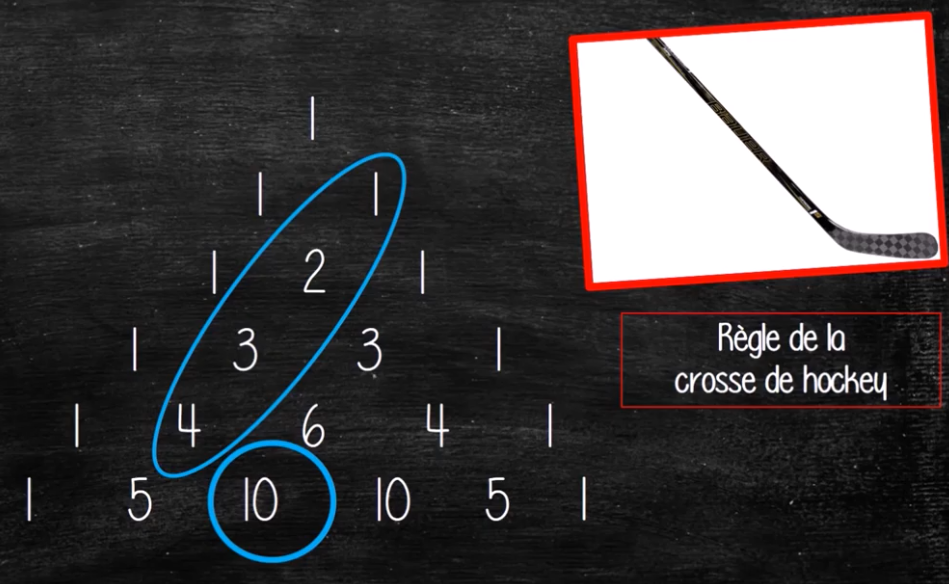
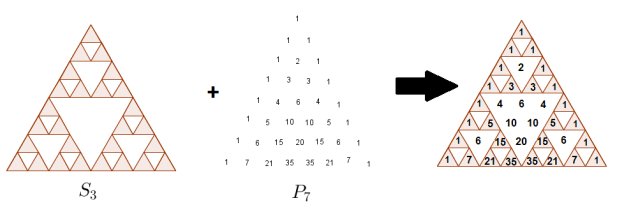
Formule liant \pi , la suite de Fibonacci et la trigonométrie :

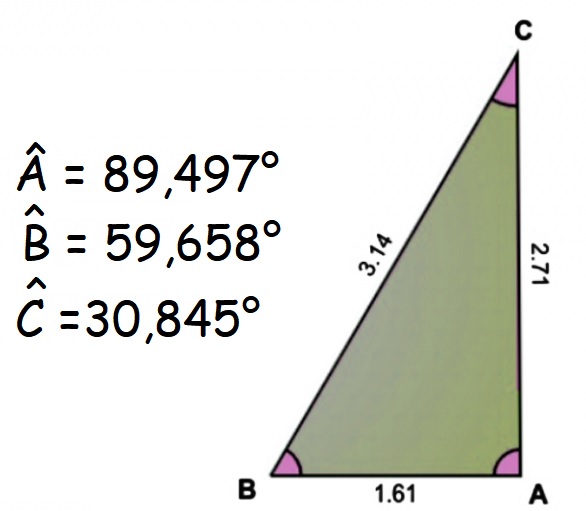
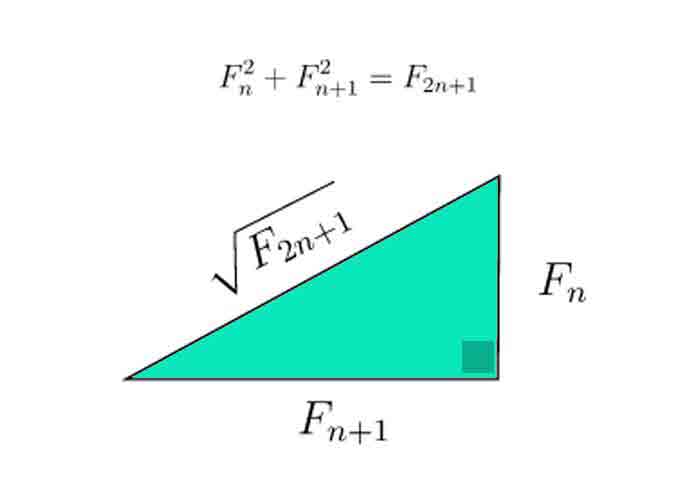
\Huge  \frac{\pi}{4}=\sum_{i=1}^{+\infty}arctan\left(\frac{1}{F_{2i+1}}\right)

II°/ Son écriture :

Sa grande particularité est qu’il possède un nombre infini de décimales. Il fait parti des nombres irrationnels qui ne peuvent donc pas s’écrire sous la forme d’une fraction de 2 nombres entiers.

Mais attention, c’est l’écriture décimale de \pi qui est infinie, ou son nombre de décimale, ce n’est pas le nombre \pi lui-même. En effet, un cercle de diamètre une unité a un périmètre de \pi unité, et c’est bien une longueur finie.

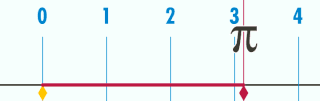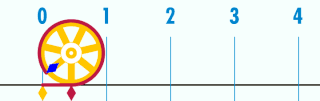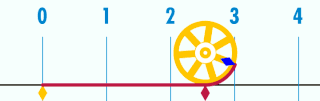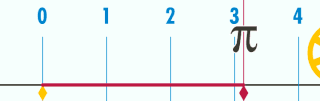
Vers -230 av JC, Archimède est capable de donner le nombre au centième prés avec sa méthode des polygones inscrits et circonscrits au cercle. Un peu plus tard,en 1420 à Samarcande en Perse, Al Kashi est capable de calculer 14 décimales de \pi.

Nous en connaissons à présent en 2 000 milliards fin 2016.

Voici les décimales de \pi au cours des âges (Pour plus de détail)

Date Mathématicien et lieu Décimales
-2500 Grande pyramide de Gizeh (Égypte) \frac{22}{7}\approx 3,142857 \ 142857 \ 142857 ...
-2000 Tablette Babylonienne découverte en 1936 \frac{25}{8}= 3,125
-1650 Le papyrus Rhind (Égypte)
Approximation du cercle par un octogone régulier.		 \left (\frac{16}{9}\right )^{2} \approx 3,16
-500 La Bible
I Roi 7:23 :Il fit la mer de fonte. Elle avait dix coudées d’un bord à l’autre, une forme entièrement ronde, cinq coudées de hauteur, et une circonférence que mesurait un cordon de trente coudées.
 3
-400 Platon (Grèce) \pi = \sqrt{2}+\sqrt{3} 3.15
-250 Archimède (Grèce)
Approximation du cercle par un polygone régulier à 96 côtés.		 \frac{223}{74}< \pi < \frac{22}{7}
5 Liu Xin (Chine) 3.1457
429–500 Zu Chongzhi 6 décimales :
\frac{355}{113}\approx 3,14159292.
499 Aryabhata (Inde) 3 décimales :
\frac{62 832}{20 000}= 3,14175
1120 Fibonacci (Léonard de Pise) (Italie) 3,141818
1592 François Viete (Un des premiers produits infinis de l’histoire). 9 décimales :
\pi = 2 \times \frac{2}{\sqrt{2}} \times \frac{2}{\sqrt{2+\sqrt{2}}} \times \frac{2}{\sqrt{2+\sqrt{2+\sqrt{2}}}} \times ...
1650 William Brouncker (1620-1687) \frac{\pi}{4 }=\frac{1}{1+\frac{1^{2}}{2+\frac{3^{2}}{2+\frac{5^{2}}{2+...}}}}
1665 Isaac Newton (Angleterre) 16 décimales :
\pi = \frac{3\sqrt{3}}{4}+24\left ( \frac{1}{3 \times 2^{2}} -\frac{1}{5 \times 2^{5}} -\frac{1}{7 \times 2^{9}} - \frac{1}{9 \times 2^{12}} ... F ...\right ) \\ F=\frac{1\times3\times...\times(2n-1) }{2\times4\times...\times(2n+2)} \times \frac{1}{2n+5} \times \frac{1}{2^{2n+4}}
1706 William Jones (Pays de Galles). Il utilise pour la première fois le symbole \pi  
1719 Thomas Fantet de Lagny (France) 112 décimales
1761 Johann Heinrich Lambert (Allemagne)Il prouve que  \pi est irrationnel, il suggère qu’il est transcendant sans le prouver.  
1788

Leonhard Euler

 \sum_{n=1 }^{\infty}\frac{1}{n^{2}}=\frac{\pi ^{2}}{6} = \frac{1}{1^{2}} +\frac{1}{2^{2}}+\frac{1}{3^{2}}... \\ \frac{\pi}{2}=\frac{3 \times 5\times7\times9\times11\times.. }{2\times6\times8\times10\times12\times...}
1913

Ramanujan

\pi = \lim_{k\rightarrow \infty }2^{k} \sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+...+\sqrt{2}}}}} Avec k la quantité de radicaux.
\frac{1}{\pi }=\frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{(k!)^{4} \times 396^{4k}}

\frac{9}{5}+\sqrt{\frac{9}{5}}=3,141 64...=\pi+0,000 05...
1946 Ferguson. Il utilise pour la première fois un calculateur informatique, une calculatrice de bureau. 620 décimales
1949 John Wrench (États-Unis) Le premier à utiliser un ordinateur (l’ENIAC) en 70 heures. 2037 décimales
1973 Jean Guilloud et Martin Bouyer (France)Sur un CDC 7600 en 23 h 20 min 1 001 250 décimales
1989 Gregory V. Chudnovsky & David V. Chudnovsky (États-Unis)Sur un CRAY-2 & IBM 3090/VF 480 000 000 décimales
2011 Alexander J. Yee et Shigeru. (Japon) 10 000 milliards de décimales
2016 Peter Trueb 22 x 1012 décimales

Voici tout plein d’autre formules plus jolies les unes que les autres !!!!

Voici les 2400 premières décimales de pi :
3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362 440 656 643 086 021 394 946 395 224 737 190 702 179 860 943 702 770 539 217 176 293 176 752 384 674 818 467 669 405 132 000 568 127 145 263 560 827 785 771 342 757 789 609 173 637 178 721 468 440 901 224 953 430 146 549 585 371 050 792 279 689 258 923 542 019 956 112 129 021 960 864 034 418 159 813 629 774 771 309 960 518 707 211 349 999 998 372 978 049 951 059 731 732 816 096 318 595 024 459 455 346 908 302 642 522 308 253 344 685 035 261 931 188 171 010 003 137 838 752 886 587 533 208 381 420 617 177 669 147 303 598 253 490 428 755 468 731 159 562 863 882 353 787 593 751 957 781 857 780 532 171 226 806 613 001 927 876 611 195 909 216 420 198 938 095 257 201 065 485 863 278 865 936 153 381 827 968 230 301 952 035 301 852 968 995 773 622 599 413 891 249 721 775 283 479 131 515 574 857 242 454 150 695 950 829 533 116 861 727 855 889 075 098 381 754 637 464 939 319 255 060 400 927 701 671 139 009 848 824 012 858 361 603 563 707 660 104 710 181 942 955 596 198 946 767 837 449 448 255 379 774 726 847 104 047 534 646 208 046 684 259 069 491 293 313 677 028 989 152 104 752 162 056 966 024 058 038 150 193 511 253 382 430 035 587 640 247 496 473 263 914 199 272 604 269 922 796 782 354 781 636 009 341 721 641 219 924 586 315 030 286 182 974 555 706 749 838 505 494 588 586 926 995 690 927 210 797 509 302 955 321 165 344 987 202 755 960 236 480 665 499 119 881 834 797 753 566 369 807 426 542 527 862 551 818 417 574 672 890 977 772 793 800 081 647 060 016 145 249 192 173 217 214 772 350 141 441 973 568 548 161 361 157 352 552 133 475 741 849 468 438 523 323 907 394 143 334 547 762 416 862 518 983 569 485 562 099 219 222 184 272 550 254 256 887 671 790 494 601 653 466 804 988 627 232 791 786 085 784 383 827 967 976 681 454 100 953 883 786 360 950 680 064 225 125 205 117 392 984 896 084 128 488 626 945 604 241 965 285 022 210 661 186 306 744 278 622 039 194 945 047 123 713 786 960 956 364 371 917 287 467 764 657 573 962 413 890 865 832 645 995 813 390 478 027 590 099 465 764 078 951 269 468 398 352 595 709 825 822 620 522 489 407 726 719 478 268 482 601 476 990 902 640 136 394 437 455 305 068 203 496 252 451 749 399 651 431 429 809 190 659 250 937 221 696 461 515 709 858 387 410 597 885 959 772 975 498 930 161 753 928 468 138 268 683 868 942 774 155 991 855 925 245 953 959 431 049 972 524 680 845 987 273 644 695 848 653 836 736 222 626 099 124 608 051 243 884 390 451 244 136 549 762 780 797 715 691 435 997 700 129 616 089 441 694 868 555 848 406 353 422 072 225 828 488 648 158 456 028 50
Pour savoir comment on les calcule, cliquez ici.

Même si ce n’est pas encore démontré, le nombre 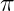est considéré comme un nombre univers, c’est à dire que c’est un nombre réel dans les décimales duquel on peut trouver n’importe quelle succession de chiffres de longueur finie. Vous pouvez ainsi vérifier sur cette page, si votre date de naissance ou votre numéro de téléphone est présent dans les décimales de 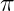. En fait on peut tout trouver dans les décimales de , à partir du moment ou on le transforme en suite de nombre. Par exemple une photo est une succession de pixel codés par un nombre représentant sa couleur, vous pouvez donc trouver n’importe quelle photo. Si on remplace les lettres par leur rang dans l’alphabet, on peut trouver n’importe quel texte dans les décimales de (Maths sera codé par M = 13, a = 1, t = 20, h = 8, s = 13 et 13120813 ce retrouve au rang 29247731) !!!!

Il existe heureusement des moyens mnémotechniques de retenir ces décimales : il s’agit de retenir des phrases dont les mots ont autant de lettres que les décimales successives (un mot de dix lettres donne la décimale 0) de .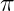

Voici par exemple un poème connu permettant de trouver les 127 premières décimales :

Que j’aime à faire apprendre ce nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur ?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l’orbe calculée approchera ;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle.

A propos : biographie de Pythagore

Et bien sûr, cette méthode est aussi utilisée à l’étranger : voici quelques exemples

Anglais

 

 Yes, I have a great statement to relate.
May I have a large container of coffee.
How I wish I could recollect of circle round
The exact relation Archimede unwound.
How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics !
How I wish I could enumerate Pi easily, since all these horrible mnemonics prevent recalling any of pi’s sequence more simply.
(ici, « pi’s » compte pour un mot)
But a time I spent wandering in bloomy night ;
Yon tower, tinkling chimewise, loftily opportune.
Out, up, and together came sudden to Sunday rite,
The one solemnly off to correct plenilune.

Allemand

 

 Dir, o Held, o Alter Philosoph, du Reisen-Genie !
Wie, viele Tausende bewundern Geister
Himmlisch wie du und Göttlich !
Noch reiner in Aeonen
Wird das uns strahlen,
Wie im lichten Morgenrot !
Wie ? O ! Dies p
Macht ernstlich so vielen viele Müh !
Lernt immerhin, Jünglinge, leichte Verselein,
Wie so zum Beispiel dies dürfte zu merken sein !

Espagnol

 Con 1 palo y 5 ladrillos se pueden hacer mil cosas.
Sol y Luna y cielo proclaman al divino autor del cosmo.

Portugais

 Sou o medo e temor constante do menino vadio.

Danois

 Eva, o lief, o zoete hartedief uw blauwe oogen zyn wreed bedrogen.

Albanais

 Kur e shoh e mesoj sigurisht.

La même technique est utilisée pour retenir d’autres nombres célèbres :

  • Les trois journées de 1830 ont renversé 89 : 1/pi = 0,3183098…
  • Tu aideras à rappeler ta quantité à beaucoup de docteurs amis : e = 2,7182818284…
  • Gamma pourras retenir, si à Euler penses chaque fois. Constante immortelle d’Euler, vas-tu toujours rester timidement cachée ? : G = 0,5772156649015328606…
  • O nombre d’élégance ! Toi, toi, grandiose, étonnant : 1,61803398, le nombre d’or.

III°/ Son calcul :

A°/ A Babylone:

On ne connait pas l’origine du nombre \pi , mais il est déjà présent 2000 av JC. Bien entendu on ne l’appelle pas encore Pi mais il est donné comme le rapport du périmètre du cercle sur son diamètre.
Le première trace de \pi apparaît sur la tablette de Suse datant de -1680 av JC.

La tablette donne l’aire de 2/25 pour un cercle de périmètre 1.

Perimetre_{cercle} = 2\pi R = 1 \ donc \ R = \frac{1}{2\pi }\\Aire_{cercle} = \pi R^{2} = \frac{2}{25} =0,08 \ donc \ \pi\times \frac{1}{4\pi ^{2}} = 0,08 \\ donc \ \pi = \frac{1}{4\times 0,08}=\frac{25}{8}=3.125

Une très bonne approximation.

B°/ En Égypte :

Il y a 4000 ans, en Égypte, il existait une méthode pour assimiler l’aire d’un disque à celle d’un carré.

Cette « recette » magique fut trouver sur le Papyrus Rhind écrit par le scribe Ahmès. Il s’agit d’une « recette » car, si elle permet de trouver une approximation au 100ième de \pi , il n’y a pas de démonstration et on ne parle pas encore du nombre \pi .

Voici ce quelle raconte : l’aire d’un disque de 9 unités de diamètre est égale à l’aire d’un carré de 8 unités de côté.

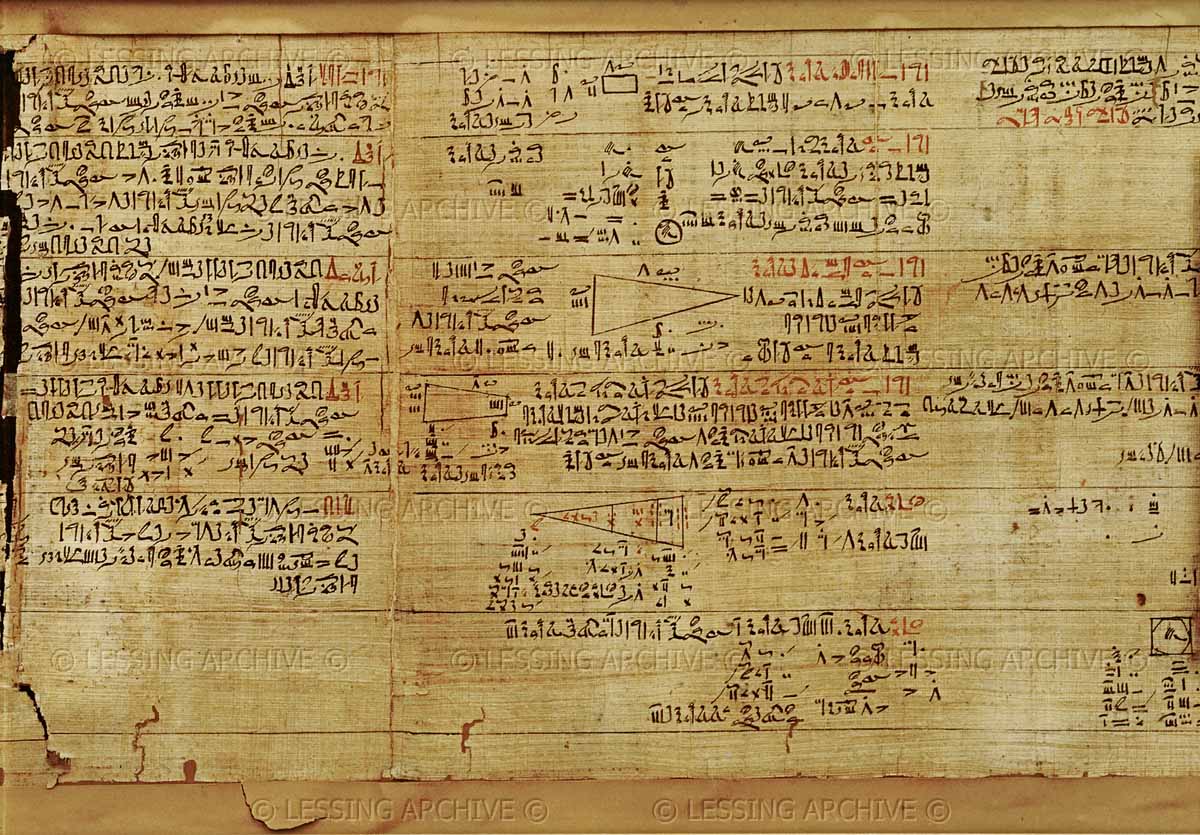Le Papyrus de Rhind est un papyrus de l’ancienne Égypte, datant de la XVème dynastie (vers 1680-1620 avant J.-C.), trouvé à Thèbes en 1858 dans les ruines d’un petit monument proche du Ramesseum par l’égyptologue écossais Alexander Henry Rhinds.
Dans un cercle de centre O et de rayon OE = 1 unité, on découpe le diamètre DF en 9 morceaux FA.

 

 

Le carré ABCD de côté AB = 8FA aura la même aire que le cercle.

Aire Disque = Aire Carré
\pi OE² = AB²
\pi = \frac{AB^{2}}{OE^{2}}=\frac{8^{2}\times FA^{2}}{4,5^{2}\times FA^{2}}=\frac{8^{2}}{4,5^{2}}\approx 3,16...

 

3,16 au lieu de 3,14 cela fait une erreur de moins de 2 centièmes, ce qui est exceptionnel pour l’époque.

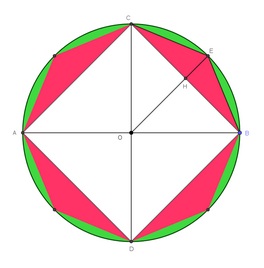
C°/ En Grèce :

Archimède en -250 av JC sera le premier à faire une démonstration.

1°/ Démonstration de la formule de l’aire du disque :

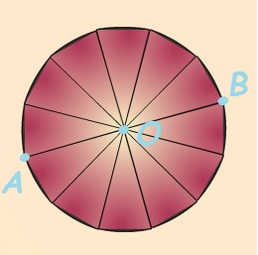
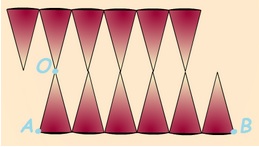
Archimède assimile l’aire d’un disque à celle d’un polygone ayant beaucoup de cotés, inscrit au disque.

 

Découpons un disque de centre O et de
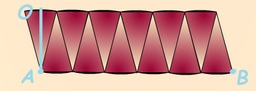
rayon R = OA en 12 parts égales.		 On déplie le disque. En réassemblant les parts on fabrique un parallélogramme.

La longueur AB représentant le demi-périmètre du cercle :

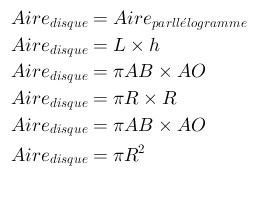Bien entendu la longueur AB n’est pas vraiment un segment, surtout si on découpe le disque en

 

 

seulement 12 parts.

Mais plus le nombre de parts sera grand et plus se sera exact.

Si on découpe le disque en un nombre infini de parts, alors les arcs de cercles noirs s’aplaniront,

AB tendra vers un segment, raisonnement sera correct et la formule du disque sera bien .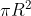

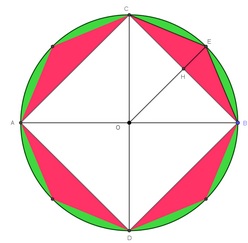
Calculons l’erreur que l’on commet en assimilant AB à un segment, c’est à dire les surfaces noires des figures au-dessus :

Commençons par découper un cercle
en 4 et traçons un carré inscrit à
l’intérieur.

 La zone verte représente la différence
entre l’aire du disque et celle du carré.
L’erreur est importante.		 Si on découpe en 8, la partie verte est
plus petite. L’aire de l’octogone se
rapproche de celle du disque.		 L’erreur verte crée par l’octogone est-elle
plus petite que celle, rouge, crée par le
carré. C’est le cas car si on rassemble les
2 secteurs circulaires verts ils sont plus
petits que l’erreur rouge.
On gagne la surface bleue.
 

2°/ Calcul du nombre \pi :

– Méthode des polygones d’Archimède : il faut encadrer un cercle de rayon 1 par des polygones inscrits et circonscrits et calculer leurs périmètres.

Dans un cercle de diamètre 1 :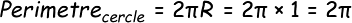

Donc :

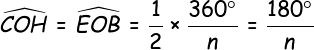
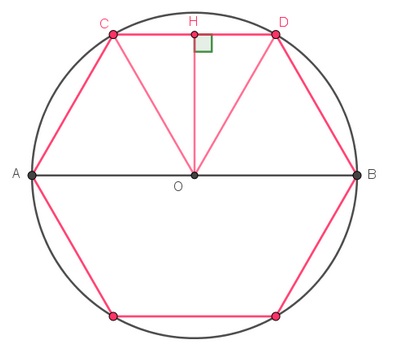
Traçons l’hexagone inscrit dans le cercle, avec n = 6. Traçons l’hexagone circonscrit au cercle, avec n = 6.
Dans le triangle COH rectangle en H.

 

 

 Dans le triangle BOE rectangle en B.

 

 

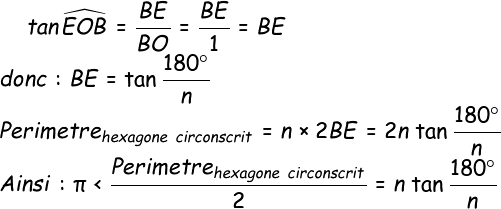
Le nombre 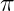sera donc obtenu par l’encadrement suivant :

Pour n = 6 on aura : 3,10582854123025 < < 3,21539030917347

Bien entendu il s’agit d’une approximation, mais si on renouvelle la démonstration en doublant le découpage du cercle (6, 12, 24, 48, 96…), au bout de 96 parts Archimède a obtenu l’encadrement suivant :

3,141 031 951 < \pi < 3,1427146

pour une valeur exacte de \pi = 3,141 592 653. L’erreur est seulement de moins de 1 millième !!!! 2 siècles avant JC c’est impressionnant.

 
 

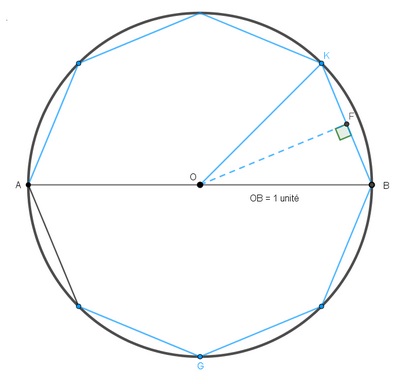
– Variante de la méthode d’Archimède, mais en calculant les aires : il faut encadrer un disque de rayon 1 par des polygones inscrits et circonscrits et calculer leurs aires.

Dans un disque de diamètre 1 :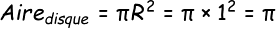

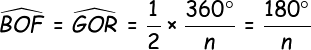
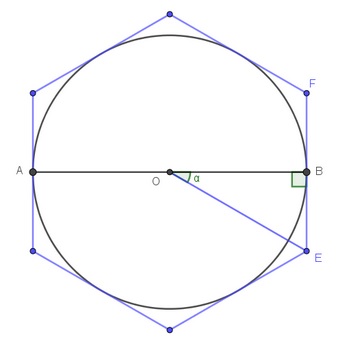
Traçons l’octogone inscrit dans le cercle, avec n = 4. Traçons l’octogone circonscrit au cercle, avec n = 4.
Dans le triangle BOF rectangle en F.

 

 

sin \ \widehat{BOF}=\frac{FB}{BO} =\frac{FB}{1}=FB
cos\ \widehat{BOF}=\frac{FO}{BO} =\frac{FO}{1}= FO

Aire_{disque \ inscrit} = \frac{apotheme \times perimetre_{polygone}}{2}

= \frac{FO\times n \times KB}{2}
= \frac{cos\ \widehat{BOF}\times n \times 2sin\ \widehat{BOF} }{2}
= n \times cos\ \widehat{BOF}\times sin\ \widehat{BOF}
= n \times cos\ \widehat{\frac{180}{n}}\times sin\ \widehat{\frac{180}{n}}

Dans le triangle GRO rectangle en G.

 

 

Le nombre 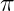sera donc obtenu par l’encadrement suivant :

Pour n = 4 on aura : 2,82842712474619 < \pi < 3,31370849898476

Là encore, il s’agit d’une approximation, mais si on renouvelle la démonstration en doublant le découpage du disque (4, 8, 16, 32, 64, 128….), au bout de 128 parts on obtient l’encadrement suivant :

3,14033115695475 < \pi < 3,14222362994246

 

Voici un fichier Excel qui donne des encadrements jusqu’à plusieurs millions de parts. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page Excel ci-dessous pour l’ouvrir dans Microsoft Office Online).

Plus simplement, on peut démontrer que 3<\pi<4 en encadrant un cercle de rayon 1 entre un hexagone de côté 1 et un carré de côté 2 :

 

D°/ Epoque moderne :

Il existe de nombreuse technique pour calculer le nombre \pi , mais il y en a une qui est très visuelle et qui utilise les fractions continues :

\pi = 3,14159265358979323846... = 3 + 0,14159265358979323846... = 3 + \frac{1}{\frac{1}{0.14159265358979323846...}} = 3 + \frac{1}{7,06251331...} \approx 3 + \frac{1}{7} = \frac{22}{7} = 3,1428 cad \pi à 2 décimales près.

Mais on peut aller plus loin :

\pi = 3 + \frac{1}{7,06251331...} = 3 + \frac{1}{7+\frac{1}{15,9965...}} = 3 + \frac{1}{7+\frac{1}{15 + 0,9965...}} = 3 + \frac{1}{7+\frac{1}{15 + \frac{1}{1+ 0,00341..}}} \approx 3 + \frac{1}{7+\frac{1}{15 + \frac{1}{1}}} = \frac{355}{113} cad \pi à 6 décimales près.

On peut ainsi, de proche en proche et au prix de très, très nombreux calculs, découvrir les décimales de \pi . Mais j’avais promis une méthode visuelle. La voici :

Plaçons un point vert sur un repère d’origine O, et construisons ses symétriques successifs par la rotation de centre O et d’angle \pi degrés. On observe la spirale de \pi . Si on construit en rouge la même rotation mais d’angle \frac{22}{7} on remarque que les points sont assez proches. Et si on construit en bleu la même rotation mais d’angle \frac{355}{113} , les points bleus et verts sont confondus. \frac{355}{113} est donc une très bonne approximation de \pi .

E°/ Le nombre Tau :

Tau est le jumeau maléfique de Pi (π). Il représente deux fois la constante Pi (3.14…), s’écrit en notation anglophone 6.28, ce qui correspond au 28 juin.

Michael Hartl, éducateur et physicien théorique, cherche depuis 2010 à faire accepter cette constante —et le «jour de Tau»— à la place de Pi —et du «jour de Pi» le 14 mars— dans les milieux mathématiques. Pour lui, il serait préférable de dire que le périmètre d’un cercle est égal à Tau fois le rayon.

Voici le cercle trigonométrique utilisant Tau pour donner les coordonnées des points du cercle.

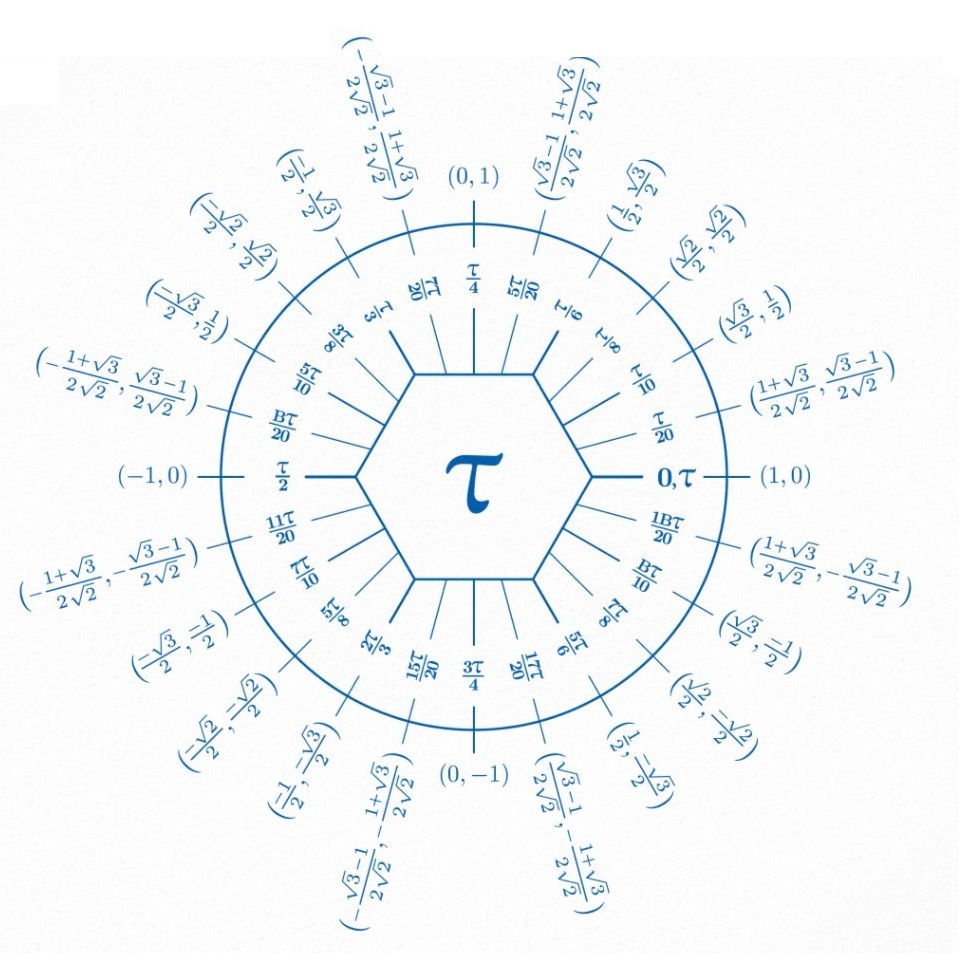IV°/ Quelques histoires originales sur \pi :

   A°/ \pi est un nombre univers :

On considère qu’il n’y a aucune suite de nombre périodique dans les décimales de \pi et que l’on peut y trouver n’importe quelle suite de chiffre. On appelle ce genre de nombre des nombres univers. On a pas encore réussit à démontrer que \pi en était un, mais cela semble certain.

Par exemple, le nombre 210615, qui est la date de naissance de Napoléon, se trouve à la position 91698. Ce nombre apparaît 225 fois dans les 200 millions premiers chiffres de \pi .

On peut numériser n’importe quelle image, musique, film ou programme, et bien ils sont tous dans les décimales de \pi .

Voici deux sites où vous amuser à retrouver votre propre date de naissance, votre poids en grammes ou tous ce que vous voulez : The Pi-Search Page ou sur le site du Palais de la découverte.

Il existe d’autres nombres univers :

  • la constante de Champernowne est 0,12345678910111213141516…, c’est à dire, le nombre dont le développement décimal est la suite des nombres entiers collés les uns aux autres. Un outil pour rechercher une suite de chiffre.
  • la constante de Copeland-Erdös, qui vaut 0,235711131719… (la suite des nombres premiers les uns à la suite des autres).

  B°/ L’Indiana pi bill :

En 1897, l’état de l’indiana vote la loie n°246 qui décrète que le nombre \pi sera désormais égal à 3,2 sur la proposition d’un médecin et mathématicien amateur Edwin J. Goodwin. La quadrature du cercle était démontrée ….

Fort heureusement cette la loi n’a jamais été adoptée, grâce à l’intervention d’un professeur de mathématiques, Clarence Abiathar Waldo (en), qui était accidentellement présent dans l’assemblée.

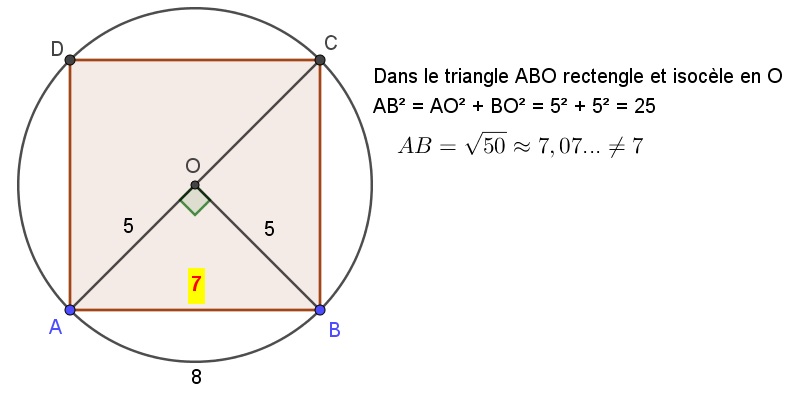Dessin paru dans le Rock Island Argus du 6 mars 1897, se moquant du projet. Schéma avec certaines dimensions qui peut être vu dans les œuvres d’Edwin J. Goodwin. Elles sont totalement fausses.

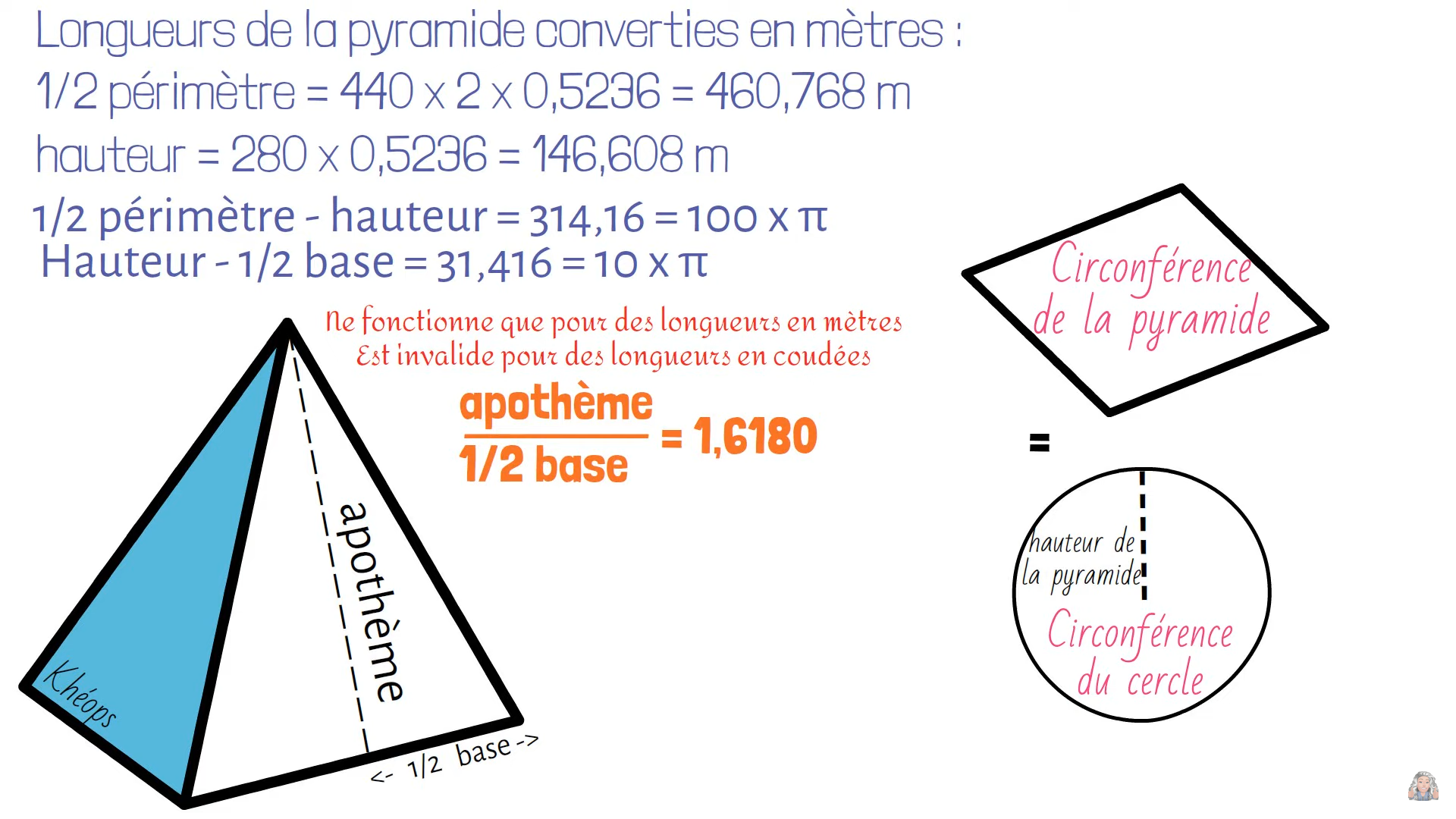
  C°/ La pyramide de Khéops :

En triturant toutes les mesures de la pyramide, on peut retrouver le nombre d’or dans de nombreux rapport. De là à affirmer que c’était voulu par les bâtisseurs …

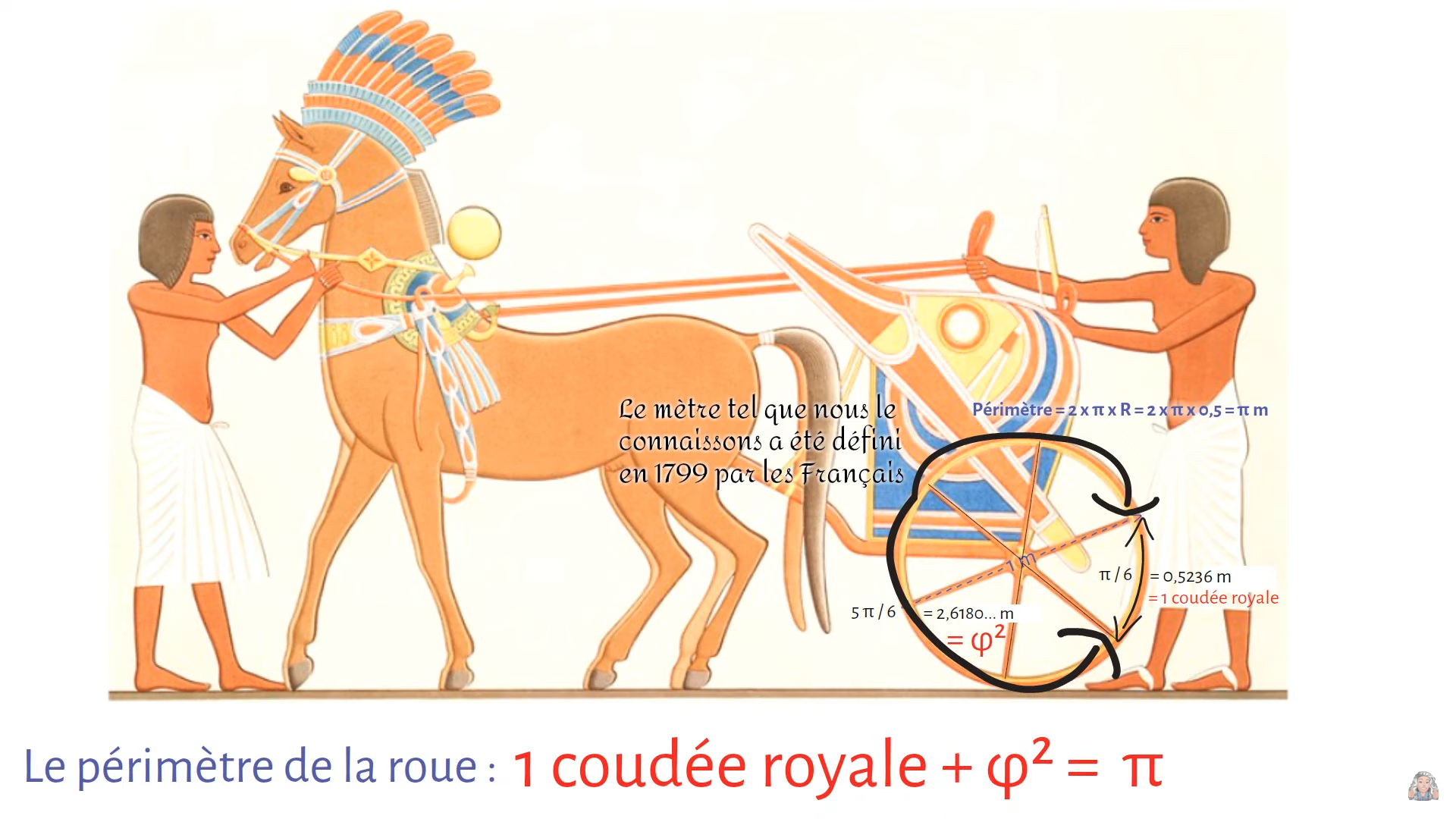
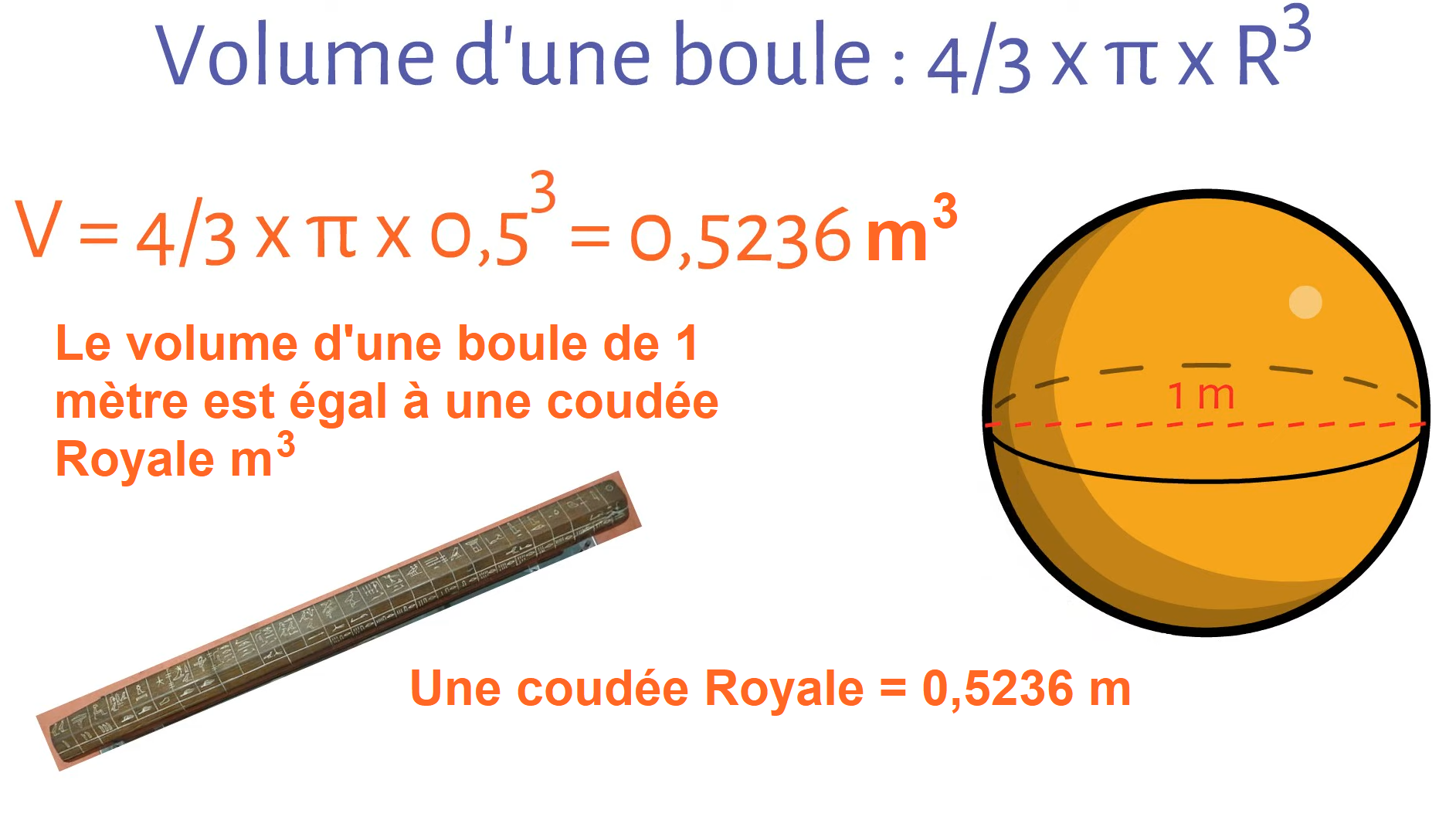
De même avec la coudée Royale qui est la mesure de référence des architectes égyptiens et qui est la longueur du bout du majeur du Pharaon jusqu’à son coude c’est à dire 52,36 cm.
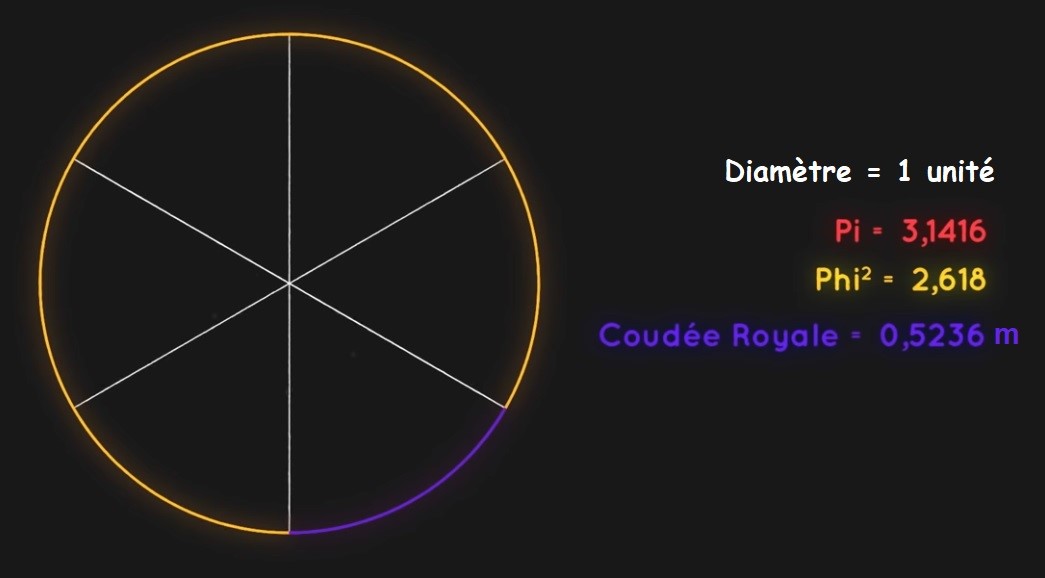
Hasard ou coïncidence, si on prend un cercle de 1 unité de diamètre alors son périmètre fera π .
La coudée royale sera le sixième de ce périmètre : \frac{\pi }{6} \approx 0,523598... \ unités
Il reste \frac{5\pi }{6} \approx 2,61799...\approx \varphi ^{2} \ unités

D°/ Amusons nous :

     

IX°/ Calcul de l’aire de n’importe quel polygone : Formule de Pick

par

I°/ Utilisation :
   A°/ En comptant les points :
   B°/ En comptant les côtés des quadrillages :
   C°/ En comptant les carrés des quadrillages :
II°/ Démonstration :
   A°/ Démonstration dans un rectangle :
   B°/ Démonstration dans un triangle rectangle :
   C°/ Démonstration dans un triangle quelconque :
   D°/ Démonstration dans un polygone quelconque :
III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky
IV°/ Le théorème de Wallace-Bolyai-Gerwien :
V°/ La formule de Euler : S – A + F = 2

 

Le théorème de Pick permet de calculer l’aire de n’importe quel polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.

I°/ Utilisation :

Dessinons un polygone sur une feuille quadrillée. Si les sommets du polygone sont sur les nœuds du quadrillage et si ce polygone n’est pas croisé, alors on peut calculer très simplement son aire, c’est à dire la mesure de sa surface.

A°/ En comptant les points : Aire = e/2 + i – 1

Soit e le nombre de points du réseau qui touchent les côtés, sommets compris (ici 14 points roses).
Soit i le nombre de points qui sont à l’intérieur de la figure (ici 12 points verts). Aire = e/2 + i – 1 = 14/2 + 12 – 1 = 18

B°/ En comptant les côtés des quadrillages : Aire = i/2 + (c+t)/4

Soit i le nombre de côtés entièrement intérieurs à la figure (32 côtés verts).
Soit c le nombre de côtés coupés intérieurs à la figure (10 côtés roses).
Soit t le nombre de côtés de carrés sur la frontière de la figure (4 côtés bleus).

Aire = i/2 + (c + t)/4

= 32/2 + (10 + 4)/4 = 16 + 3,5 = 19,5

C°/ En comptant les carrés des quadrillages : Aire = e + c/2

Soit e le nombre de mailles entièrement à l’intérieur de la figure (7 ronds verts).
Soit c le nombre de mailles coupées par la frontière de la figure (11 ronds roses). Aire = e + c/2= 7 + 11/2 = 12,5

Entrainez-vous avec ce polygone :

Ou alors :

II°/ Démonstration :

Si : i = le nombre de points à l’intérieur du polygone.
b = le nombre de points sur les bords (côtés) du polygone.

Aire_{polygone}=i+ \frac{b}{2}-1

A°/ Démonstration dans un rectangle :

1°/ Par le calcul : Soit un rectangle ABCD de longueur AB et de largeur BC.

Points verts : i = (AB – 1)(BC – 1)

Points rouges : b = 2x(AB + BC)

Donc :

Aire_{polygone}=i+ \frac{b}{2}-1

= ABxBC – AB – BC + 1 + AB + BC – 1 = ABxBC

Donc la formule de Pick nous donne bien la formule générale de l’aire d’un rectangle : Longueur fois largeur.

Dans l’exemple :

Aire_{rectangle}=i+\frac{b}{2}-1=24+\frac{24}{2}-1=24+12-1=35 u^{2}

Aire_{rectangle}=L \times l =7 \times 5=35 u2

La formule de Pick est vérifiée pour les rectangles.

2°/ Par la géométrie : Soit un rectangle ABCD de longueur AB et de largeur BC.

Décalons le quadrillage d’un demi carreau pour intégrer les points verts dans des carrés de même surface que les carrés représentés par 4 points de couleurs.

Nombre de carrés verts contenant les points verts : (AB – 1)(BC – 1) = ABxBC –AB – BC + 1

Nombre de rectangles roses contenant les points rouges : 2 x [(AB – 1) + (BC – 1)] = 2AB + 2BC – 4

Nombre de carrés rouges contenant les points rouges : 4

Donc : Points verts : i = (AB – 1)(BC – 1) = ABxBC –AB – BC + 1

Points rouges : b = 2AB + 2BC – 4 + 4 = 2AB + 2BC

Aire_{rectangle}=i+ \frac{b}{2}-1 = ABxBC –AB – BC + 1 + AB + BC -1 = ABxBC = Longueur fois largeur.

B°/ Démonstration dans un triangle rectangle :

Un triangle rectangle est la moitié d’un rectangle. Donc :

Points verts du triangle : it

Points rouges des côtés perpendiculaires du triangle : bt

Points rouges de l’hypoténuse du triangle sans les extrémités : h

Points verts du rectangle (ceux des 2 triangles plus ceux présents sur l’hypoténuse) : ir = 2 it + h

Points rouges du rectangle (ceux des 2 triangles, sans les 2 hypoténuses, moins 2 sommets comptés 2 fois) : br = 2 bt – 2h – 2

Aire_{rectangle}=i+ \frac{b}{2}-1= 2 it + h + bt – h – 1 – 1 = 2it + bt – 2 = 2\times (i_{t}+\frac{b_{t}}{2} -1)

Aire_{rectangle}=2 \times Aire_{triangle}
La formule de Pick est vérifiée pour les triangles rectangles.

C°/ Démonstration dans un triangle quelconque :

On peut inscrire un triangle quelconque dans un rectangle. t1 = AED ; t2 = EBF; t3 = FCD et t = CDE

Points verts du rectangle ABCD (ceux des 4 triangles plus ceux présents sur les hypoténuses des 3 triangles rectangles) :

ir = it1 + h1 + it2 + h2 + it3 + h3 + it

Points rouges du rectangle (ceux des 3 triangles t1, t2 et t3, sans leurs hypoténuses, moins 6 sommets comptés 2 fois pour chacun des 3 triangles) :

br = bt1 – h1 + bt2 – h2 + bt3 – h3 – 6

De plus les points sur les bords du triangle CDE sont ceux présents sur les 3 hypoténuses : bt = h1 + h2 + h3

Aire_{CDE}=Aire_{ABCD}-Aire_{AED}-Aire_{EBF}-Aire_{FCD}

Aire_{CDE}=i_{R}+\frac{b_{r}}{2}-1-i_{T1}-\frac{b_{T1}}{2}+1-i_{T2}-\frac{b_{T2}}{2}+1-i_{T3}-\frac{b_{T3}}{2}+1

La formule de Pick est vérifiée pour les triangles quelconques.

Vérification sur l’exemple : Aire_{DEF}=i_{t}+ \frac{b_{t}}{2}-1 = 14 + \frac{6}{2}-1 = 16 unités d’aire

D°/ Démonstration dans un polygone quelconque :

Tout polygone peut être découpé en triangles, donc le théorème de Pick est à présent démontrer pour tout polygone non croisé et sans trou, et dont les sommets sont sur les sommets d’un quadrillage.

III°/ Théorème de mémère – pépère : Plus exactement le théorème de même aire p pair ou Théorème de Monsky

Ce théorème vaut par son titre amusant (à dire rapidement : mémère – pépère …), qui n’en est pas moins exact.

Il dit que si on peut découper un carré en triangles de même aires, alors il y a un nombre pair de triangle.

Autrement dit de façon Mathématiques mais mois rigolo, un carré n’admet pas d’équidissection impaire.

On peut généraliser ce théorème à tous les polygones.

Il y a 8 triangles de même aire dans le premier carré et 6 de même aire dans le second. Par contre dans le troisième carré rouge, il y a 7 triangles dont les deux verts n’ont pas la même aire que les autres.

IV°/ Le théorème de Wallace-Bolyai-Gerwien : les formules des aires des polygones et des volumes des solides

Les matheux aiment le découpage : la preuve avec le théorème de Wallace-Bolyai-Gerwien et avec le théorème de Dehn !

Dans cette vidéo de El JJ nous verront comment retrouver les formules des aires des polygones et des volumes des solides par découpage, comment passer d’un polygone ou d’un polyèdre à un autre toujours par découpage et enfin nous découvrirons le 3ième problème de Hilbert.

V°/ La formule de Euler : S – A + F = 2

Pour les polygones, la formule d’Euler affirme que : S + R = A + 2 (S nombre de sommets, R nombre de régions délimitées par les arêtes et A nombre d’arêtes)

1 points + 1 points = + 1 arêtes, donc pas de changement dans la formule. + 1 région sans sommet = + 1 arête
Schéma
Sommet S S = 1 S + 1 = 1 + 1 = 2 S + 4 = 5 S = 5
Régions R R = 1 R = 1 R = 1 R = 2 + 1 = 3
Arêtes A A = 0 A + 1 = 0 + 1 = 1 A + 4 A = 5 + 1 = 6
Formule d’Euler
S + R = A + 2		 1 + 1 = 0 + 2 = 2 2 + 1 = 1 + 2 = 3
S + 1 + R = A + 1 + 2
S + R = A + 2		 5 + 1 = 4 + 2 = 6
S + 4 + R = A + 4 + 2
S + R = A + 2		 5 + 3 = 6 + 2 = 8
S + R + 1 = A + 1 + 2
S + R = A + 2

Tour de magie :

Cette formule permet de créer un petit tour de magie assez bluffant : gribouiller n’importe comment. La seule chose qui importe, c’est que le gribouillage soit en un seul morceau (connexe). Par exemple, vous pouvez faire un truc comme ça :

C’est maintenant qu’on va faire des maths ! Dans ce gribouillage, on peut repérer des « Sommets » S (les points d’intersection et les extrémités), des « Arrêtes » A (ce qui relie deux sommets) et des « Régions » R (les cellules, délimitées par des arrêtes. Au passage, l’extérieur de la figure est une face. On les appellent souvent Face F.). Comptez-les !

Moi, je compte S = 26 sommets (bleus), A = 49 arrêtes (rouges) et F = 25 faces (verts)

Attention, tour de magie qui n’impressionnera personne. Je suis sûr que si vous effectuez l’opération S – A + F = 26 – 49 + 25 = 2, vous trouverez toujours 2 !

La formule d’Euler pour les polyèdres convexes : S + F = A + 2 (S nombre de sommets, F nombre de faces et A nombre d’arêtes).

Une très belle vidéo :

Vertices = sommets

Edges = arêtes

Faces = faces

Dans un polyèdre : Nombre de sommet – Nombre d’arêtes  + Nombre de face = 2

S – A + F = 2

Ou en Anglais : V – E + F = 2

XIV°/ Le format A4 des feuilles :

par

L’idéal pour une feuille, serait que son format ne change pas lorsqu’on la plie en deux ou que l’on fait un agrandissement ou une réduction avec une photocopieuse.

Pour cela le rapport Longueur sur largeur doit être constant d’un format à l’autre, et pour que l’on puisse plier parfaitement une feuille en deux.

Quel doit être ce rapport ?

Dans le tableau excel suivant, on se rend compte que si on prend une Longueur 2 fois plus grande que la largeur, le format suivant est un carré de rapport 1, puis le suivant un rectangle de rapport 2 et ainsi de suite. Avec les images qui suivent où la Longueur de départ est le double de la largeur, le burro Catalan grossit puis revient aux bonnes proportions au fil des réductions.

Utilisez ce fichier Excel pour fabriquer vos propres formats : Format A4. http://trabucaire.free.fr/wp-content/uploads/2020/07/Racine-carree-compte-goutte.xlsx

Format B4 où le rapport L/l n’est constant.

Pour que les images ne se déforment pas, quel doit être le bon rapport ?

Soit L la longueur d’une feuille et l sa largeur.

Lorsqu’on la coupe en deux, la largeur de la nouvelle feuille est la moitié de la Longueur précédente,  et sa longueur est maintenant l.

Pour avoir la même forme il faut que le rapport des deux mesures soit identique :

\frac{Ancienne \ Longueur \ L}{Ancienne \ largeur \ l} = \frac{Nouvelle\ Longueur \ l}{Nouvelle\ largeur \ L/2} \Rightarrow \frac{L^{2}}{l^{2}}=2 \Rightarrow \frac{L}{l} = \sqrt{2}\approx 1,414

La première référence au rapport \sqrt{2} ce trouve dans une lettre écrite le 25 octobre 1786 par le professeur de physique Georg Christoph Lichtenberg (Université de Göttingen, Allemagne, 1742-1799) à Johann Beckmann. Il se trouve que le papier sur lequel était écrit cette lettre respecté justement ce rapport de \sqrt{2} entre la Longueur et la largeur.

L’Organisation Internationale de Normalisation (ISO) constitua en 1947 le Comité Technique ISO/TC 6 « papier » qui chargea un de ses sous-comités d’étudier les dimensions internationales des papiers et des cartons. La recommandation fut demandée d’envisager la normalisation des formats.

Comme nous l’avons vu ci-dessus, lorsqu’on plie en deux une feuille A4, le format reste identique : le rapport longueur sur largeur de la feuille reste constant. C’est très pratique. Ainsi nous passons du format A3 au format A4, en pliant des feuilles A3 en deux, puis du format A4 au format A5 en pliant également en deux une feuille A4.

Le format de départ A0 est défini comme ayant une surface mesurant 1 m². Quelles seront ces dimensions ?

L\times l=1\;donc\;l=\frac{1}{L}\\\frac{L}{l}=\sqrt{2}\;donc\;\frac{L}{\frac{1}{L}}=\sqrt{2}=L^{2}\\L=\sqrt{\sqrt{2}}=1,189207115 \ m^{2}=118,9 \ cm^{2}\\l=\frac{1}{\sqrt{\sqrt{2}}}=0,8408964153 \ m^{2}=84,1 \ cm^{2}
Format Longueur en cm largeur en cm Rapport Aire en m² Poids en g
A0 118,9 84,1 \frac{118,9}{84,1} =1,413794 1 80
A1 84,1 59,5 \frac{84,1}{59,5} =1,413445 1/2 40
A2 59,5 42 \frac{59,5}{42} =1,416667 1/4 20
A3 42 29,7 \frac{42}{29,7} =1,414141 1/8 10
A4 29,7 21 \frac{29,7}{21} =1,414286 1/16 5
A5 21 14,8 \frac{21}{14,8} =1,418919 1/32 2,5

Ainsi le rapport Longueur/Largeur est identique pour toutes les feuilles et chacune contient exactement deux feuilles du format immédiatement inférieur.

Notons qu’avec du papier 80g/m², une feuille A4 d’aire 1/16 m² pèse 5g. Nous pouvons donc placer 3 feuilles dans une enveloppe et mettre un timbre normal sur l’enveloppe (moins de 20g).

XV°/ Les preuves par 9 et par 11 :

par

a/ La preuve par 9 :

Cette preuve qui est encore utilisée à bon escient dans certaines classes.
Tout de même cette preuve n’en a que le nom, car si elle est fausse c’est certain, notre opération est fausse. Mais si elle tombe juste alors l’opération est peut-être bonne… cependant ce n’est pas sûr, car 2 erreurs peuvent s’annuler.
Toutefois elle est intéressante car elle fait réfléchir sur la technique de l’opération.

Habituellement elle est utilisée pour la multiplication et la division, mais elle peut être également utilisée pour l’addition et la soustraction.

Elle repose sur le principe suivant : on refait l’opération désirée en remplaçant chacun des nombres par son reste dans la division par 9.

Ce reste sera un nombre de 0 à 8.

On sait que ce reste est le même que celui de la somme des chiffres du nombre. Chaque fois qu’il y a un 9, on peut le remplacer par 0.

On recommence le procédé jusqu’à ce qu’on obtienne un nombre plus petit que 9.

Ainsi pour le nombre 7 854 672 on obtiendra d’abord 7 + 8 + 5 + 4 + 6 + 7 + 2 soit 39 qui va donner 3.

3 est le reste de 7 854 672 dans la division par 9. Vous pouvez le vérifier.

Si on le désire on peut remplacer chaque somme partielle comme 7 + 8 = 15 par 1 + 5 = 6 et ainsi de suite…

Voici un fichier Excel pour vous entrainer : La preuve par 9. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)

b/ La preuve par 11 :

Le principe est le même que celui de la preuve par 9, mais on utilise cette fois le critère de divisibilité par 11.

Comme il fait appel à une soustraction, il n’est pas enseigné à l’école primaire parce qu’on peut tomber sur un nombre négatif avec la soustraction.

On sait que ce reste est le même que celui de la somme des chiffres de rang impair en partant de la droite moins la somme des chiffres de rang pair en partant de la droite.

C’est un peu compliqué à dire mais facile à mettre en œuvre voici un exemple :

Ainsi pour le nombre 79 859 632 on fera : (2 + 6 + 5 + 9) – (3 + 9 + 8 + 7) = 22 – 27

Nous sommes dans le cas où 27 est plus grand que 22. Alors on ajoute à 22 autant de fois de 11 qu’il le faut, pour obtenir une soustraction avec un résultat positif : 22 + 11 = 33

Et le nombre a même reste que 33 – 27 soit 6.

On recommence jusqu’à obtenir un nombre plus petit que 11.

Voici un fichier Excel pour vous entrainer : La preuve par 11. (Fichier à télécharger ou cliquez sur la flèche en haut à droite de la page excel ci-dessous pour l’ouvrir dans Microsoft Office Online)